第 1 章 绪论
1.1 定义
Performance:计算机程序在某任务类T上的性能。
Task:计算机程序希望实现的任务类。
Experience:表示经验,即历史的数据集。
人的“经验”对应计算机中的“数据”,让计算机来学习这些经验数据,生成一个算法模型,在面对新的情况中,计算机便能做出有效的判断,这便是机器学习。
1.2 基本术语
所有记录的集合为:数据集(dataset)
每一条记录为:一个实例(instance)或样本(sample)
单个样本的特点为特征(feature)或属性(attribute)
一个样本的特征数为:维数(dimensionality)
关于样本结果的信息称为标记(label)
通过执行某个学习算法,从数据中学得模型的过程称为“学习” (learning)或“训练” (training)。
学得模型后,使用其进行预测的过程称为“测试”(testing),被预测的样本称为“测试样本”(testing sample)。
所有训练样本的集合为:训练集(training set)
所有测试样本的集合为:测试集(test set)
机器学习出来的模型适用于新样本的能力为:泛化能力(generalization)
预测值为离散值的问题为:分类(classification)
预测值为连续值的问题为:回归(regression)
训练数据有标记信息的学习任务为:监督学习(supervised learning),分类和回归都是监督学习的范畴。
训练数据没有标记信息的学习任务为:无监督学习(unsupervised learning),常见的有聚类和关联规则。
1.3 假设空间
假设空间就是由所有假设组成的集合。一个假设就是一种映射方法,它把具有某些特定属性值的西瓜映射为“好瓜”,其余西瓜映射为“坏瓜”。
机器学习中的模型是由输入空间到输出空间的映射的集合,也就是由输入空间 X 到输出空间 Y 的映射 f : X→Y 所构成的集合,该空间是一个函数空间,即假设空间是由函数所构成的集合。
版本空间就是与训练集一致的所有假设所构成的集合。
周志华老师《机器学习》假设空间和版本空间概念辨析 - 知乎
1.4 归纳偏好
机器学习算法在学习过程中对某种类型的假设的偏好,称为归纳偏好(inductive bias)
给定训练数据集的情况下,通过添加额外的限制条件或标准去帮助模型更好地拟合训练集,同时还促使模型在未知样本数据集上也有很好的预测能力(即泛化能力),那么这些额外的限制条件或标准就是归纳偏好。
有监督学习的归纳偏置简述_飞机火车巴雷特的博客-CSDN博客_归纳偏置能力
归纳偏好对模型本身关于“什么样的模型好”通过先验知识(奥卡姆)作了假设。
奥卡姆剃刀原则认为:若有多个假设与观察一致,则选最简单的那个。
免费午餐定理((No Free Lunch Theorem):没有一个学习算法可以在所有情况下总是产生最准确的模型。在脱离实际意义情况下,空泛地谈论哪种算法好毫无意义,要谈论算法优劣必须针对具体学习问题。
没有免费午餐定理No Free Lunch Theorem_飞机火车巴雷特的博客-CSDN博客_没有免费午餐定理
第 2 章 绪论
2.1 误差与过拟合
误差(error):学习器对样本的实际预测结果与样本的真实值之间的差异。
在训练集上的误差称为训练误差(training error)或经验误差(empirical error)。
在测试集上的误差称为测试误差(test error)
学习器在所有新样本上的误差称为泛化误差(generalization error)
过拟合(overfitting):学习能力过强,以至于把训练样本所包含的不太一般的特性都学到了。
欠拟合(underfitting):学习能太差,训练样本的一般性质尚未学好。
在过拟合问题中,训练误差十分小,但测试误差教大;在欠拟合问题中,训练误差和测试误差都比较大。
目前,欠拟合问题比较容易克服,例如增加迭代次数等,但过拟合问题还没有十分好的解决方案,过拟合是机器学习面临的关键障碍。
2.2 评估方法
我们希望得到的是泛化误差小的学习器,理想的解决方案是对模型的泛化误差进行评估,然后选择泛化误差最小的学习器。但是,泛化误差指的是模型在所有新样本上的适用能力,我们无法直接获得泛化误差。
通常我们采用一个“测试集”来测试学习器对新样本的判别能力,然后以“测试集”上的“测试误差”作为“泛化误差”的近似。
划分测试集和训练集的方法
留出法:
将数据集D划分为两个互斥的集合,一个作为训练集S,一个作为测试集T,80%的样本用作训练,20%用作测试。常见的划分为:训练集/测试集 = 2/1~4/1。
训练/测试集划分时要保持数据分布一致性,即保证训练集和测试集中类别比例一致,可采用分层采样。
交叉验证法:
将数据集划分为k个大小相同的互斥子集,同样地尽可能保持数据分布的一致性,即采用分层抽样的方法获得这些子集。
交叉验证法的思想是:每次用k-1个子集的并集作为训练集,余下的那个子集作为测试集,这样就有种训练集/测试集划分的情况,从而可进行次训练和测试,最终返回次测试结果的均值。
交叉验证法也称“ 折交叉验证”,k最常用的取值是10 ,即10折交叉验证。
与留出法类似,将数据集D划分为个子集的过程具有随机性,因此K折交叉证通常也要重复次,称为p次k折交叉验证,常见的是10次10折交叉验证,即进行了100次训练/测试。
特殊地当划分的k个子集的每个子集中只有一个样本时,称为“留一法”,显然,留一法的评估结果比较准确,但对计算机的消耗也是巨大的。
自助法:
给定包含 m个样本的数据集 D,对它进行采样产生数据集 D′ ,每次随机从 D 中挑选一个样本,将其拷贝放入 D′,然后再将这个样本放回初始数据集 D,使得该样本在下次采样时仍可能被采样到,重复此过程 m次,得到包含 m个训练样本的数据集 D′。 D中样本在 m次采样中始终不被采样到的概率是 ( 1 − m )m 取极限得到(0.368)。
通过自助采样,输出数据集 D中约有36.8%的样本未出现在采样数据集D′ 中,于是用 D′做训练集, D − D′做测试集。
自助法在数据集较小、难以有效划分训练/测试集时很有用。此外,自助法能从初始数据集中产生多个不同的训练集,这对集成学习等方法又很大的好处。
自助法产生的数据集改变了初始数据集的分布,这会引入估计偏差,因此在初始数据量足够是,留出法和交叉验证法更常用。
2.3 性能度量
性能度量是“测试误差”的一个评价标准。有了评估方法和性能度量,就可以计算出学习器的“测试误差”。
性能度量(performance measure)是衡量模型泛化能力的评价标准,在对比不同模型的能力时,使用不同的性能度量往往会导致不同的评判结果。
常见的性能度量:
均方误差(mean squared error,MSE),用于回归任务
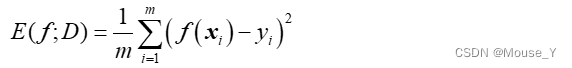
在分类任务中,最常用的是错误率和精度


错误率是分类错误的样本数占样本总数的比例
精度则是分类正确的样本数占样本总数的比例
查准率和查全率
对于二类分类问题,常用的评价指标是查准率(precision)与查全率(recall)。通常以关注的类为正类,其他类为负类,分类器在测试数据集上的预测或正确或不正确,4 种情况出现的总数分别记作:
真正例(True Positive,TP)——将正类预测为正类数;
假负例(False Negative,FN)——将正类预测为负类数;
假正例(False Positive,FP)——将负类预测为正类数;
真负例(True Negative,TN)——将负类预测为负类数。
精确率定义为

召回率定义为

F1值,是精确率和召回率的调和均值,即

精确率和召回率都高时,F1值也会高。
ROC****与AUC
召回率也称为真正例率(True positive rate,TPR),定义了在训练过程中所有可用的阳性样本中有多少正确的阳性结果。
假正例率(False positive rate,FPR)定义了训练过程中所有可用的阴性样本中错误阳性结果的数量,即FPR 。
将TPR和FPR绘制分别作为横轴和纵轴,可以绘制受试者工作特征曲线(Receiver operating characteristic curve,ROC),描述了真阳性(收益)和假阳性(成本)之间的相对权衡。
进行学习器的比较时
若一个学习器的ROC 曲线被另一个学习器的曲线完全“包住”, 则可断言后者的性能优于前者
若两个学习器的ROC 曲线发生交叉,则难以-般性地断言两者孰优孰劣。
此时如果一定要进行比较, 则较为合理的判据是比较ROC 曲线下的面积,即AUC (Area Under ROC Curve)
2.4 比较检验
2.5 偏差与方差
版权归原作者 Mouse_Y 所有, 如有侵权,请联系我们删除。