目录
0 写在前面
机器学习强基计划聚焦深度和广度,加深对机器学习模型的理解与应用。“深”在详细推导算法模型背后的数学原理;“广”在分析多个机器学习模型:决策树、支持向量机、贝叶斯与马尔科夫决策、强化学习等。
🚀详情:机器学习强基计划(附几十种经典模型源码合集)
1 什么是Logistic回归?
在机器学习强基计划1-1:图文详解感知机算法原理+Python实现提到广义线性模型(generalized linear model)
f
(
x
(
i
)
)
=
g
−
1
(
w
T
x
(
i
)
+
b
)
f\left( \boldsymbol{x}^{\left( i \right)} \right) =g^{-1}\left( \boldsymbol{w}^T\boldsymbol{x}^{\left( i \right)}+b \right)
f(x(i))=g−1(wTx(i)+b)
其中单调可微函数
g
(
⋅
)
g\left( \cdot \right)
g(⋅)称为**联系函数(link function)**。广义线性模型本质上仍是线性的,但通过
g
(
⋅
)
g\left( \cdot \right)
g(⋅)进行非线性映射,使之具有更强的拟合能力,类似神经元的激活函数。
Logistic回归是
g
−
1
(
z
)
=
1
1
+
e
−
z
g^{-1}\left( z \right) =\frac{1}{1+e^{-z}}
g−1(z)=1+e−z1时的广义线性模型,
g
−
1
(
z
)
=
1
1
+
e
−
z
g^{-1}\left( z \right) =\frac{1}{1+e^{-z}}
g−1(z)=1+e−z1这个函数在人工智能领域非常著名,称为**sigmoid函数**,其值被限定在0-1区间内,因此也可认为是概率映射。
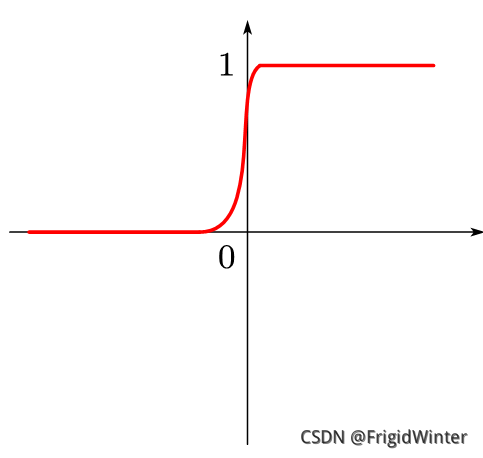
所以Logistic回归可以认为输出了预测类别的概率,因此Logistic回归本质上是在线性回归基础上,将预测值映射到概率区间内的分类学习方法。
常见的Logisitc回归类型如表所示。
Logistic回归分析类型输出标签举例说明二元Logistic回归是/否分类数据,且仅分为两类多元无序Logistic回归一线城市、二线城市、三线城市分类数据,分类超过两类且同类别之间没有对比意义多元有序Logistic回归不同意、无所谓、同意分类数据,分类超过两类且同类别之间具有对比意义
本节讨论最简单的二元Logistic回归。
2 手推Logistic回归原理
首先列出Logistic回归的表达式:
f
(
x
^
(
i
)
)
=
g
−
1
(
w
^
T
x
^
(
i
)
)
⇔
w
^
T
x
^
(
i
)
=
ln
f
(
x
^
(
i
)
)
1
−
f
(
x
^
(
i
)
)
f\left( \boldsymbol{\hat{x}}^{\left( i \right)} \right) =g^{-1}\left( \boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}^{\left( i \right)} \right) \Leftrightarrow \boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}^{\left( i \right)}=\ln \frac{f\left( \boldsymbol{\hat{x}}^{\left( i \right)} \right)}{1-f\left( \boldsymbol{\hat{x}}^{\left( i \right)} \right)}
f(x^(i))=g−1(w^Tx^(i))⇔w^Tx^(i)=ln1−f(x^(i))f(x^(i))
可将输出
f
(
x
^
(
i
)
)
f\left( \boldsymbol{\hat{x}}^{\left( i \right)} \right)
f(x^(i))视为给定一个训练样本
x
^
(
i
)
\boldsymbol{\hat{x}}^{\left( i \right)}
x^(i)输出预测类别的后验概率
p
(
y
i
=
1
∣
x
^
(
i
)
)
p\left( y_i=1|\boldsymbol{\hat{x}}^{\left( i \right)} \right)
p(yi=1∣x^(i))。
这里涉及一些概率论方面的知识,关于概率、似然等概念请参考机器学习强基计划4-1:你真的分得清频率、概率、几率和似然吗?
接下来根据极大似然法估计参数向量
w
^
\boldsymbol{\hat{w}}
w^,即**获得在给定观测样本的条件下,最接近样本真实标签的参数组合**,令损失函数
E
(
w
^
)
=
∑
i
=
1
m
ln
p
(
y
i
∣
x
^
(
i
)
;
w
^
)
E\left( \boldsymbol{\hat{w}} \right) =\sum\nolimits_{i=1}^m{\ln p\left( y_i|\boldsymbol{\hat{x}}^{\left( i \right)};\boldsymbol{\hat{w}} \right)}
E(w^)=∑i=1mlnp(yi∣x^(i);w^),考虑二分类情形:
{
p
(
y
i
=
1
∣
x
^
(
i
)
;
w
^
)
=
y
i
p
(
y
i
=
1
∣
x
^
(
i
)
;
w
^
)
p
(
y
i
=
0
∣
x
^
(
i
)
;
w
^
)
=
(
1
−
y
i
)
p
(
y
i
=
0
∣
x
^
(
i
)
;
w
^
)
⇒
E
(
w
^
)
=
∑
i
=
1
m
y
i
ln
p
(
y
i
=
1
∣
x
^
(
i
)
;
w
^
)
+
(
1
−
y
i
)
ln
(
1
−
p
(
y
i
=
1
∣
x
^
(
i
)
;
w
^
)
)
\begin{cases} p\left( y_i=1|\boldsymbol{\hat{x}}^{\left( i \right)};\boldsymbol{\hat{w}} \right) =y_ip\left( y_i=1|\boldsymbol{\hat{x}}^{\left( i \right)};\boldsymbol{\hat{w}} \right)\\ p\left( y_i=0|\boldsymbol{\hat{x}}^{\left( i \right)};\boldsymbol{\hat{w}} \right) =\left( 1-y_i \right) p\left( y_i=0|\boldsymbol{\hat{x}}^{\left( i \right)};\boldsymbol{\hat{w}} \right)\\\end{cases}\\\Rightarrow E\left( \boldsymbol{\hat{w}} \right) =\sum_{i=1}^m{y_i\ln p\left( y_i=1|\boldsymbol{\hat{x}}^{\left( i \right)};\boldsymbol{\hat{w}} \right) +\left( 1-y_i \right) \ln \left( 1-p\left( y_i=1|\boldsymbol{\hat{x}}^{\left( i \right)};\boldsymbol{\hat{w}} \right) \right)}
⎩⎨⎧p(yi=1∣x^(i);w^)=yip(yi=1∣x^(i);w^)p(yi=0∣x^(i);w^)=(1−yi)p(yi=0∣x^(i);w^)⇒E(w^)=i=1∑myilnp(yi=1∣x^(i);w^)+(1−yi)ln(1−p(yi=1∣x^(i);w^))
这里再次用到感知机算法推导时的技巧。
代入
p
(
y
i
=
1
∣
x
^
(
i
)
)
=
1
1
+
e
−
w
^
T
x
^
(
i
)
=
e
w
^
T
x
^
(
i
)
1
+
e
w
^
T
x
^
(
i
)
p\left( y_i=1|\boldsymbol{\hat{x}}^{\left( i \right)} \right) =\frac{1}{1+e^{-\boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}^{\left( i \right)}}}=\frac{e^{\boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}^{\left( i \right)}}}{1+e^{\boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}^{\left( i \right)}}}
p(yi=1∣x^(i))=1+e−w^Tx^(i)1=1+ew^Tx^(i)ew^Tx^(i)即得
E
(
w
^
)
=
∑
i
=
1
m
(
y
i
w
^
T
x
^
(
i
)
−
ln
(
1
+
e
w
^
T
x
^
(
i
)
)
)
⇒
w
^
∗
=
−
a
r
g
min
w
^
E
(
w
^
)
E\left( \boldsymbol{\hat{w}} \right) =\sum_{i=1}^m{\left( y_i\boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}^{\left( i \right)}-\ln \left( 1+e^{\boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}^{\left( i \right)}} \right) \right)}\Rightarrow \boldsymbol{\hat{w}}^*=\underset{\boldsymbol{\hat{w}}}{-\mathrm{arg}\min}E\left( \boldsymbol{\hat{w}} \right)
E(w^)=i=1∑m(yiw^Tx^(i)−ln(1+ew^Tx^(i)))⇒w^∗=w^−argminE(w^)
考虑到
E
(
w
^
)
E\left( \boldsymbol{\hat{w}} \right)
E(w^)是高阶可导连续凸函数,因此可用最优化理论求解,例如:
- 梯度下降算法
- 牛顿迭代算法
这里以梯度下降算法为例求解Logistic回归:
∂
E
(
w
^
)
∂
w
^
=
∑
i
=
1
m
(
y
i
x
^
(
i
)
−
x
^
(
i
)
e
w
^
T
x
^
(
i
)
1
+
e
w
^
T
x
^
(
i
)
)
=
∑
i
=
1
m
(
y
i
−
s
i
g
m
o
i
d
(
w
^
T
x
^
(
i
)
)
)
x
^
(
i
)
\frac{\partial E\left( \boldsymbol{\hat{w}} \right)}{\partial \boldsymbol{\hat{w}}}=\sum_{i=1}^m{\left( y_i\boldsymbol{\hat{x}}^{\left( i \right)}-\frac{\boldsymbol{\hat{x}}^{\left( i \right)}e^{\boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}^{\left( i \right)}}}{1+e^{\boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}^{\left( i \right)}}} \right)} \\ =\sum_{i=1}^m{\left( y_i-\mathrm{sigmoid}\left( \boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}^{\left( i \right)} \right) \right)}\boldsymbol{\hat{x}}^{\left( i \right)}
∂w^∂E(w^)=i=1∑m(yix^(i)−1+ew^Tx^(i)x^(i)ew^Tx^(i))=i=1∑m(yi−sigmoid(w^Tx^(i)))x^(i)
来分析一下这个式子的物理意义:
w
^
\boldsymbol{\hat{w}}
w^是模型的参数,
y
i
y_i
yi是真实标签,
s
i
g
m
o
i
d
(
.
)
\mathrm{sigmoid}(.)
sigmoid(.)输出的是预测概率,那也就是说
- 假如 y i = 0 y_i=0 yi=0为反例, s i g m o i d ( w ^ T x ^ ( i ) ) \mathrm{sigmoid}\left( \boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}^{\left( i \right)} \right) sigmoid(w^Tx^(i))就应该越接近0,损失越小;
- 假如 y i = 1 y_i=1 yi=1为正例, s i g m o i d ( w ^ T x ^ ( i ) ) \mathrm{sigmoid}\left( \boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}^{\left( i \right)} \right) sigmoid(w^Tx^(i))就应该越接近1,损失越小;
设损失向量
y
~
=
[
y
1
−
s
i
g
m
o
i
d
(
w
^
T
x
^
(
1
)
)
y
2
−
s
i
g
m
o
i
d
(
w
^
T
x
^
(
2
)
)
⋮
y
m
−
s
i
g
m
o
i
d
(
w
^
T
x
^
(
m
)
)
]
\boldsymbol{\tilde{y}}=\left[ \begin{array}{c} y_1-\mathrm{sigmoid}\left( \boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}^{\left( 1 \right)} \right)\\ y_2-\mathrm{sigmoid}\left( \boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}^{\left( 2 \right)} \right)\\ \vdots\\ y_m-\mathrm{sigmoid}\left( \boldsymbol{\hat{w}}^T\boldsymbol{\hat{x}}^{\left( m \right)} \right)\\ \end{array} \right]
y~=⎣⎡y1−sigmoid(w^Tx^(1))y2−sigmoid(w^Tx^(2))⋮ym−sigmoid(w^Tx^(m))⎦⎤
则
∂
E
(
w
^
)
∂
w
^
=
X
^
y
~
\frac{\partial E\left( \boldsymbol{\hat{w}} \right)}{\partial \boldsymbol{\hat{w}}}=\boldsymbol{\hat{X}\tilde{y}}
∂w^∂E(w^)=X^y~
根据梯度下降公式:
w
^
k
+
1
=
w
^
k
−
γ
∂
E
(
w
^
)
∂
w
^
\boldsymbol{\hat{w}}_{k+1}=\boldsymbol{\hat{w}}_k-\gamma \frac{\partial E\left( \boldsymbol{\hat{w}} \right)}{\partial \boldsymbol{\hat{w}}}
w^k+1=w^k−γ∂w^∂E(w^)
一直迭代直至收敛即可。
3 Python实现
3.1 创建分类器
对数几率回归对象,
X
为样本属性矩阵,
y
为样本标签矩阵
classLogit:def__init__(self, X, y)->None:# 样本齐次属性矩阵
self.X = np.row_stack((np.stack([X[col]for col in X]), np.ones(shape=(1, X.index.size))))# 样本数
self.N = np.size(self.X,1)# 样本标签 [y1, y2, ..., ym]^T
self.y = np.array(y).reshape(len(y),1)# 权重参数 [w1, w2, ..., wd, b]^T
self.w = np.ones((np.size(self.X,0),1))
3.2 定义优化过程
func
是调用的学习算法(函数指针),
iteration
是迭代学习次数,
learningRate
是学习率,对应公式
w
^
k
+
1
=
w
^
k
−
γ
∂
E
(
w
^
)
∂
w
^
\boldsymbol{\hat{w}}_{k+1}=\boldsymbol{\hat{w}}_k-\gamma \frac{\partial E\left( \boldsymbol{\hat{w}} \right)}{\partial \boldsymbol{\hat{w}}}
w^k+1=w^k−γ∂w^∂E(w^)
deflogitRegression(self, func, iteration=700, learningRate=0.5):for i inrange(iteration):
self.w = self.w - learningRate * func()print("第{}次迭代,损失{}".format(i, self.cost()))
3.3 优化函数
对应公式
∂
E
(
w
^
)
∂
w
^
=
X
^
y
~
\frac{\partial E\left( \boldsymbol{\hat{w}} \right)}{\partial \boldsymbol{\hat{w}}}=\boldsymbol{\hat{X}\tilde{y}}
∂w^∂E(w^)=X^y~
defgradientDescent(self):
wTx = np.dot(self.w.T, self.X).reshape(-1,1)
dw =-self.X.dot(self.y - Logit.sigmod(wTx))return dw
3.4 可视化
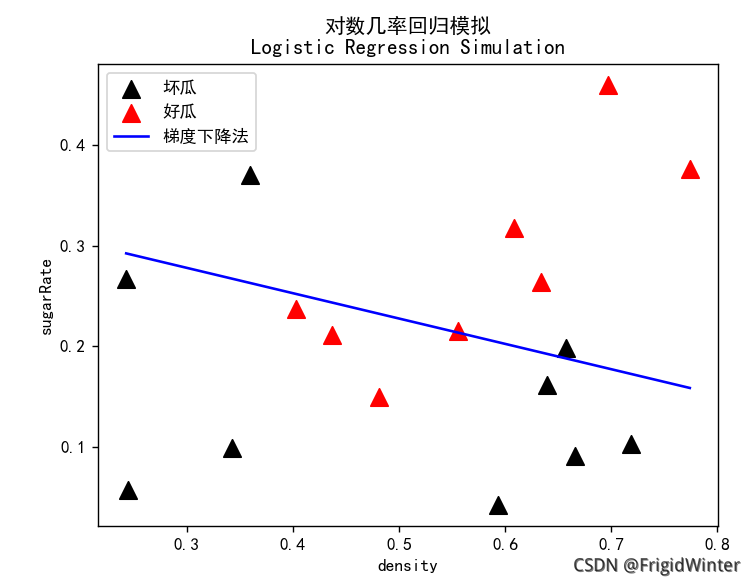
logit = Logit(dataX, label)# 采用梯度下降法
logit.logitRegression(logit.gradientDescent)
line_y =-logit.w[0,0]/ logit.w[1,0]* line_x - logit.w[2,0]/ logit.w[1,0]
plt.plot(line_x, line_y,'b-', label="梯度下降法")# 绘图
plt.legend(loc='upper left')
plt.show()
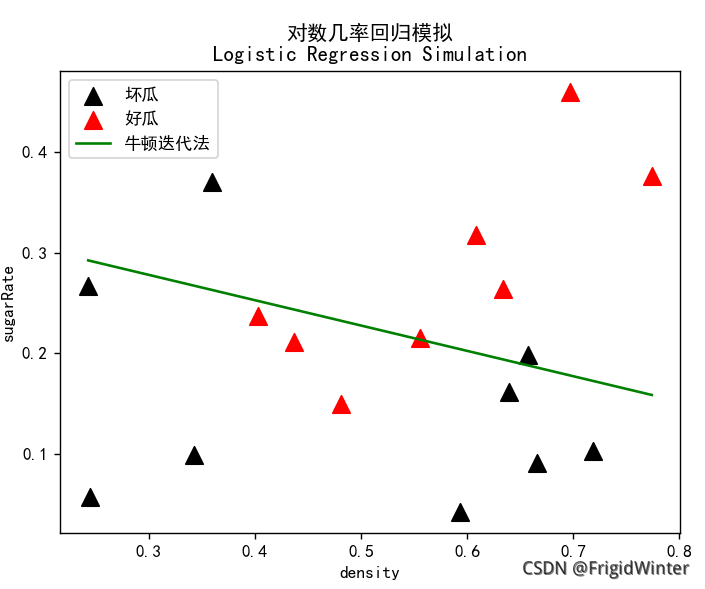
采用牛顿迭代法也类似:
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《机器人原理与技术》
- 《机器学习强基计划》
- 《计算机视觉教程》
- …
👇源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系👇
版权归原作者 Mr.Winter` 所有, 如有侵权,请联系我们删除。