⚡About—>车神:从寝室到实验室最快3分钟,最慢3分半(那半分钟其实是等红绿灯)
📝个人主页:车手只需要车和手,压力来自论文_府学路18号车神_CSDN博客
有限元法( FEM )是一种流行的方法,用于数值求解工程和数学建模中出现的微分方程。感兴趣的典型问题领域包括结构分析、传热、流体流动、质量传递和电磁势等传统领域。

“有限元”重定向至此。对于一个偏序的元素,请参阅紧凑元素。
有限元法原理
有限元法是求解两个或三个空间变量的偏微分方程(即一些边值问题)的通用数值方法。为了解决一个问题,FEM 将一个大系统细分为更小、更简单的部分,这些部分称为有限元。这是通过空间维度中的特定空间离散化来实现的,该离散化是通过构建对象的网格来实现的:解的数值域,它具有有限数量的点。边值问题的有限元法公式化最终产生代数方程组. 该方法在域上逼近未知函数。然后将模拟这些有限元的简单方程组合成一个更大的方程组,以模拟整个问题。然后,FEM 通过变分法最小化相关误差函数来近似解。
- *使用 FEM研究或分析现象通常称为**有限元分析( FEA )*。
基本概念
将整个域细分为更简单的部分有几个优点:
- 复杂几何图形的精确表示
- 包含不同的材料特性
- 整体解决方案的简单表示
- 捕捉局部效应
该方法的典型工作包括:
- 将问题的域划分为子域的集合,每个子域由原始问题的一组元素方程表示
- 系统地将所有元素方程组重新组合成一个全局方程组,以进行最终计算
全局方程组具有已知的求解技术,并且可以从原始问题的初始值计算得到数值答案。
在上面的第一步中,元素方程是局部近似要研究的原始复杂方程的简单方程,其中原始方程通常是偏微分方程(PDE)。为了解释这个过程中的近似,通常引入有限元法作为Galerkin 方法的一个特例。用数学语言来说,这个过程是构造残差和权重函数的内积的积分并将积分设置为零。简单来说,它是一个通过将试验函数拟合到 PDE 中来最小化近似误差的过程。残差是试验函数引起的误差,权重函数是多项式的投影残差的近似函数。该过程消除了 PDE 中的所有空间导数,从而在局部近似 PDE
- 一组用于稳态问题的代数方程
- 一组用于瞬态问题的常微分方程
这些方程组是元素方程。如果基础 PDE 是线性的,则它们是线性的,反之亦然。稳态问题中出现的代数方程组使用数值线性代数方法求解,而瞬态问题中出现的常微分方程组使用标准技术(例如欧拉法或龙格-库塔法)通过数值积分求解。
在上面的步骤(2)中,通过从子域的局部节点到域的全局节点的坐标变换,从元素方程生成全局方程组。这种空间变换包括与参考坐标系相关的适当方向调整。该过程通常由 FEM 软件使用从子域生成的坐标数据来执行。
FEM 的实际应用称为有限元分析(FEA)。在工程中应用的 FEA是一种用于执行工程分析的计算工具。它包括使用网格生成技术将复杂问题划分为小元素,以及使用有限元算法编码的软件。在应用 FEA 时,复杂问题通常是具有基础物理的物理系统,例如Euler-Bernoulli 梁方程、热方程或Navier-Stokes 方程,以 PDE 或积分方程表示,而复杂问题的划分的小元素代表物理系统中的不同区域。
FEA 可用于分析复杂域(如汽车和输油管道)、域发生变化时(如在与移动边界发生固态反应期间)、所需精度在整个域内发生变化时或求解时的问题。缺乏平滑度。FEA 模拟提供了宝贵的资源,因为它们消除了针对各种高保真情况创建和测试硬原型的多个实例。例如,在正面碰撞模拟中,可以提高汽车前部等“重要”区域的预测精度,并降低其后部的预测精度(从而降低模拟成本)。另一个例子是数值天气预报,在这种情况下,对发展高度非线性的现象(例如大气中的热带气旋或海洋中的涡流)进行准确预测比相对平静的区域更重要。
技术讨论
有限元方法的结构
有限元方法的特征在于变分公式、离散化策略、一个或多个求解算法和后处理程序。
变分公式的例子有Galerkin 方法、不连续 Galerkin 方法、混合方法等。
离散化策略是指一组明确定义的程序,包括 (a) 有限元网格的创建,(b) 参考单元上的基函数(也称为形状函数)的定义和 © 参考映射元素到网格的元素上。离散化策略的例子有 h-version、p-version、hp-version、x-FEM、isogeometric analysis等。每种离散化策略都有一定的优缺点。选择离散化策略的合理标准是在特定模型类中为最广泛的数学模型集实现近乎最佳的性能。
各种数值求解算法可分为两大类;直接和迭代求解器。这些算法旨在利用依赖于变分公式和离散化策略选择的矩阵的稀疏性。
后处理程序设计用于从有限元解中提取感兴趣的数据。为了满足解决方案验证的要求,后处理器需要根据感兴趣的数量提供后验误差估计。当近似误差大于被认为可接受的误差时,离散化必须通过自动自适应过程或分析师的行动来改变。有一些非常有效的后处理器可以实现超收敛。
说明性问题 P1 和 P2
以下两个问题演示了有限元方法。
P1 是一个一维问题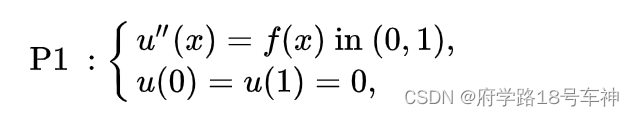
其中
f
{\displaystyle f}
f给出,
u
{\displaystyle u}
u是一个与
x
{\displaystyle x}
x相关的未知函数, 且
u
′
′
{\displaystyle u''}
u′′是
u
{\displaystyle u}
u关于
x
{\displaystyle x}
x的二阶导数.
P2 是一个二维问题(狄利克雷问题)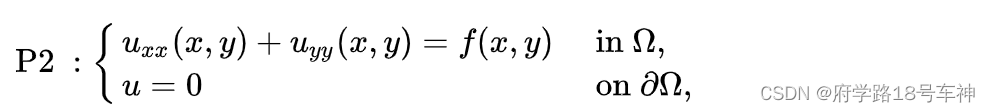
其中
Ω
{\displaystyle \Omega }
Ω是一个连通的开放区域
(
x
,
y
)
{\displaystyle (x,y)}
(x,y)边界的平面
∂
Ω
{\displaystyle \partial \Omega }
∂Ω部分很好(例如,平滑流形或多边形),并且
u
x
x
{\displaystyle u_{xx}}
uxx和
u
y
y
{\displaystyle u_{yy}}
uyy表示关于的二阶导数
x
{\displaystyle x}
x和
y
{\displaystyle y}
y是的。
问题 P1 可以直接通过计算反导数来解决。但是,这种解决边值问题(BVP) 的方法仅在存在一个空间维度时才有效,并且不能推广到更高维度的问题或类似问题
u
+
u
′
′
=
f
u
+
u
′
′
=
f
.
{\displaystyle u+u''=f}u+u''=f.
u+u′′=fu+u′′=f. 出于这个原因,我们将开发 P1 的有限元方法并将其推广到 P2。
我们的解释将分两个步骤进行,这反映了使用 FEM 解决边界值问题 (BVP) 必须采取的两个基本步骤。
- 第一步,将原始 BVP 改写为弱形式。此步骤通常几乎不需要计算。转换是在纸上手工完成的。
- 第二步是离散化,其中弱形式在有限维空间中被离散化。
在这第二步之后,我们有一个大型但有限维线性问题的具体公式,其解决方案将近似解决原始 BVP。然后在计算机上实现这个有限维问题。
弱公式
第一步是将 P1 和 P2 转换为等效的弱公式。
P1 的弱形式
如果
u
{\displaystyle u}
u你求解 P1,然后求解任何平滑函数
v
{\displaystyle v}
v满足位移边界条件,即
v
=
0
{\displaystyle v=0}
v=0在
x
=
0
{\displaystyle x=0}
x=0和
x
=
1
{\displaystyle x=1}
x=1, 我们有
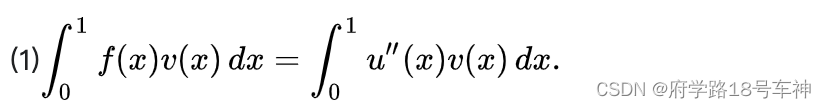
相反,如果
u
{\displaystyle u}
u你和
u
(
0
)
=
u
(
1
)
=
0
{\displaystyle u(0)=u(1)=0}
u(0)=u(1)=0对于每个平滑函数满足 (1)
v
(
x
)
{\displaystyle v(x)}
v(x)那么人们可能会证明这一点
u
{\displaystyle u}
u你将解决 P1。两次连续可微的证明更容易
u
{\displaystyle u}
u(中值定理),但也可以在分布意义上证明。
我们定义一个新的运算符或映射
ϕ
(
u
,
v
)
{\displaystyle \phi (u,v)}
ϕ(u,v)通过使用(1) 右侧的 部分积分:
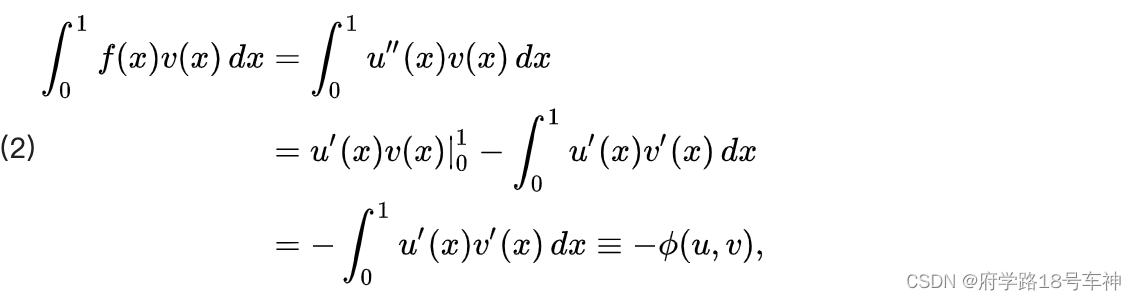
我们使用的假设是
v
(
0
)
=
v
(
1
)
=
0
{\displaystyle v(0)=v(1)=0}
v(0)=v(1)=0 ,
v
(
0
)
=
v
(
1
)
=
0
{\displaystyle v(0)=v(1)=0}
v(0)=v(1)=0.
P2的弱形式
如果我们使用格林恒等式的形式进行部分整合,我们会看到,如果
u
{\displaystyle u}
u你求解 P2,那么我们可以定义
ϕ
(
u
,
v
)
{\displaystyle \phi (u,v)}
ϕ(u,v)对于任何
v
{\displaystyle v}
v经过
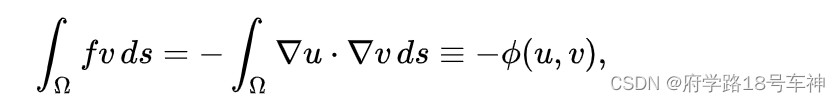
其中
∇
{\displaystyle \nabla }
∇表示梯度和
⋅
{\displaystyle \cdot }
⋅表示二维平面上的点积。再一次
ϕ
{\displaystyle \,\!\phi }
ϕ可以在合适的空间变成内积
H
0
1
(
Ω
)
{\displaystyle H_{0}^{1}(\Omega )}
H01(Ω)的一次可微函数
Ω
{\displaystyle \Omega }
Ω是零
∂
Ω
{\displaystyle \partial \Omega }
∂Ω. 我们还假设
v
∈
H
0
1
(
Ω
)
v
∈
H
0
1
{\displaystyle v\in H_{0}^{1}(\Omega )}v \in H_0^1
v∈H01(Ω)v∈H01参见Sobolev 空间)。还可以显示解决方案的存在性和唯一性。
解决方案存在性和唯一性的证明大纲
我们可以容易地想到${\displaystyle H_{0}^{1}(0,1)}$是的绝对连续函数
(
0
,
1
)
{\displaystyle (0,1)}
(0,1)那是
0
{\displaystyle 0}
0在
x
=
0
{\displaystyle x=0}
x=0和
x
=
1
{\displaystyle x=1}
x=1(参见Sobolev 空间)。这样的函数是(弱)一次可微的,事实证明对称双线性映射
ϕ
{\displaystyle \!\,\phi }
ϕ然后定义一个内积
H
0
1
(
0
,
1
)
{\displaystyle H_{0}^{1}(0,1)}
H01(0,1)进入希尔伯特空间(详细的证明是复杂的)。另一方面,左侧
∫
0
1
f
(
x
)
v
(
x
)
d
x
{\displaystyle \int _{0}^{1}f(x)v(x)dx}
∫01f(x)v(x)dx也是内积,这次在Lp空间
L
2
(
0
,
1
)
{\displaystyle L^{2}(0,1)}
L2(0,1). 希尔伯特空间的Riesz 表示定理的应用表明存在唯一的
u
{\displaystyle u}
u你求解(2),因此 P1。这个解决方案是先验的
H
0
1
(
0
,
1
)
{\displaystyle H_{0}^{1}(0,1)}
H01(0,1)使用椭圆规律,如果
f
{\displaystyle f}
f是。
离散化
P1 和 P2 已准备好被离散化,这导致了一个共同的子问题 (3)。基本思想是替换无限维线性问题: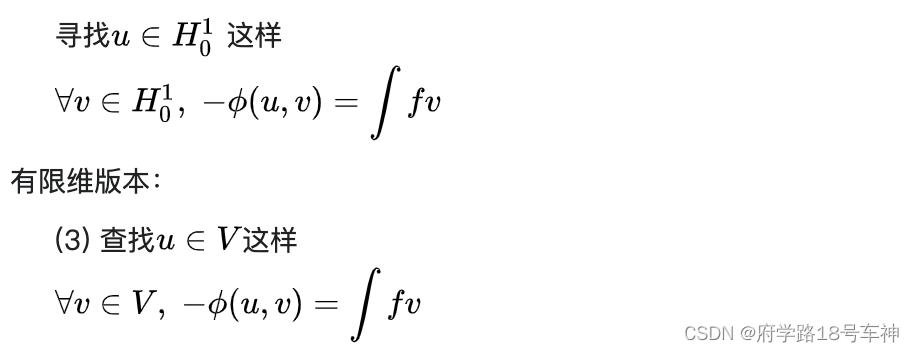
其中
V
{\displaystyle V}
V五是一个有限维子空间
H
0
1
{\displaystyle H_{0}^{1}}
H01 有很多可能的选择
V
{\displaystyle V}
V五(一种可能性导致光谱法)。然而,对于有限元方法,我们采用
V
{\displaystyle V}
V五是一个分段多项式函数的空间。
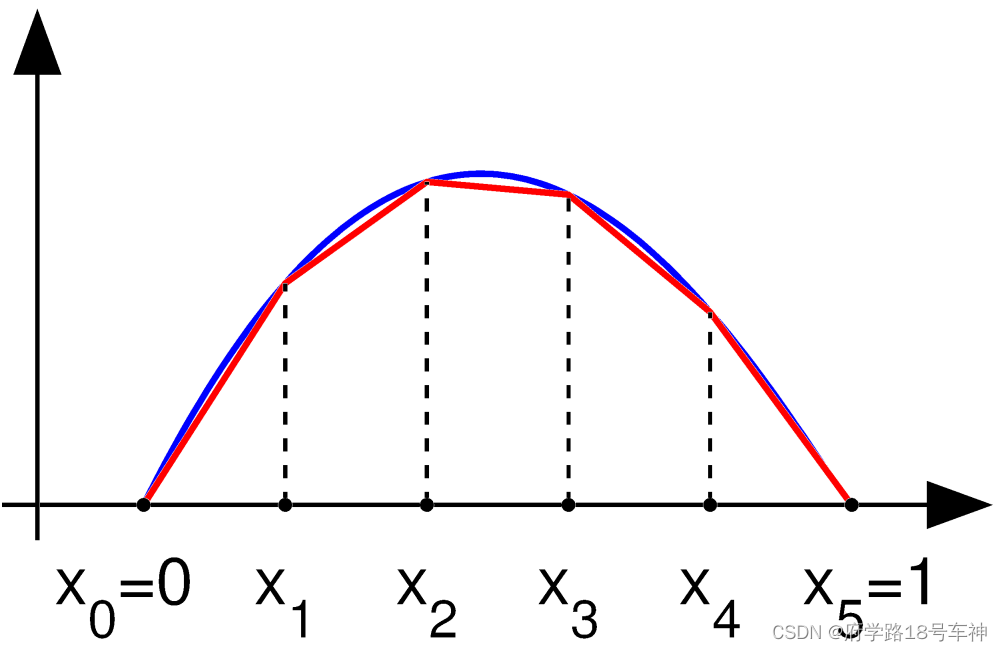
对于问题 P1
我们取区间
(
0
,
1
)
{\displaystyle (0,1)}
(0,1), 选择
n
{\displaystyle n}
n的值
x
{\displaystyle x}
x和
0
=
x
0
<
x
1
<
⋯
<
x
n
<
x
n
+
1
=
1
{\displaystyle 0=x_{0}<x_{1}<\cdots <x_{n}<x_{n+1}=1}
0=x0<x1<⋯<xn<xn+1=1我们定义
V
{\displaystyle V}
V经过:
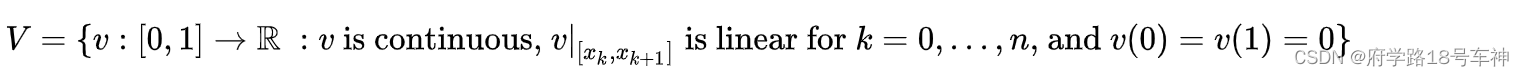
我们定义的地方
x
0
=
0
{\displaystyle x_{0}=0}
x0=0和
x
n
+
1
=
1
{\displaystyle x_{n+1}=1}
xn+1=1. 观察函数
V
{\displaystyle V}
V根据微积分的基本定义是不可微的。确实,如果
v
∈
V
{\displaystyle v\in V}
v∈V那么导数通常没有定义
x
=
x
k
{\displaystyle x=x_{k}}
x=xk,
k
=
1
,
…
,
n
{\displaystyle k=1,\ldots ,n}
k=1,…,n点,n. 然而,导数存在于每隔一个值
x
{\displaystyle x}
x并且可以将这种导数用于按部分集成的目的。
对于问题 P2
我们需要
V
{\displaystyle V}
V是一组函数
Ω
{\displaystyle \Omega }
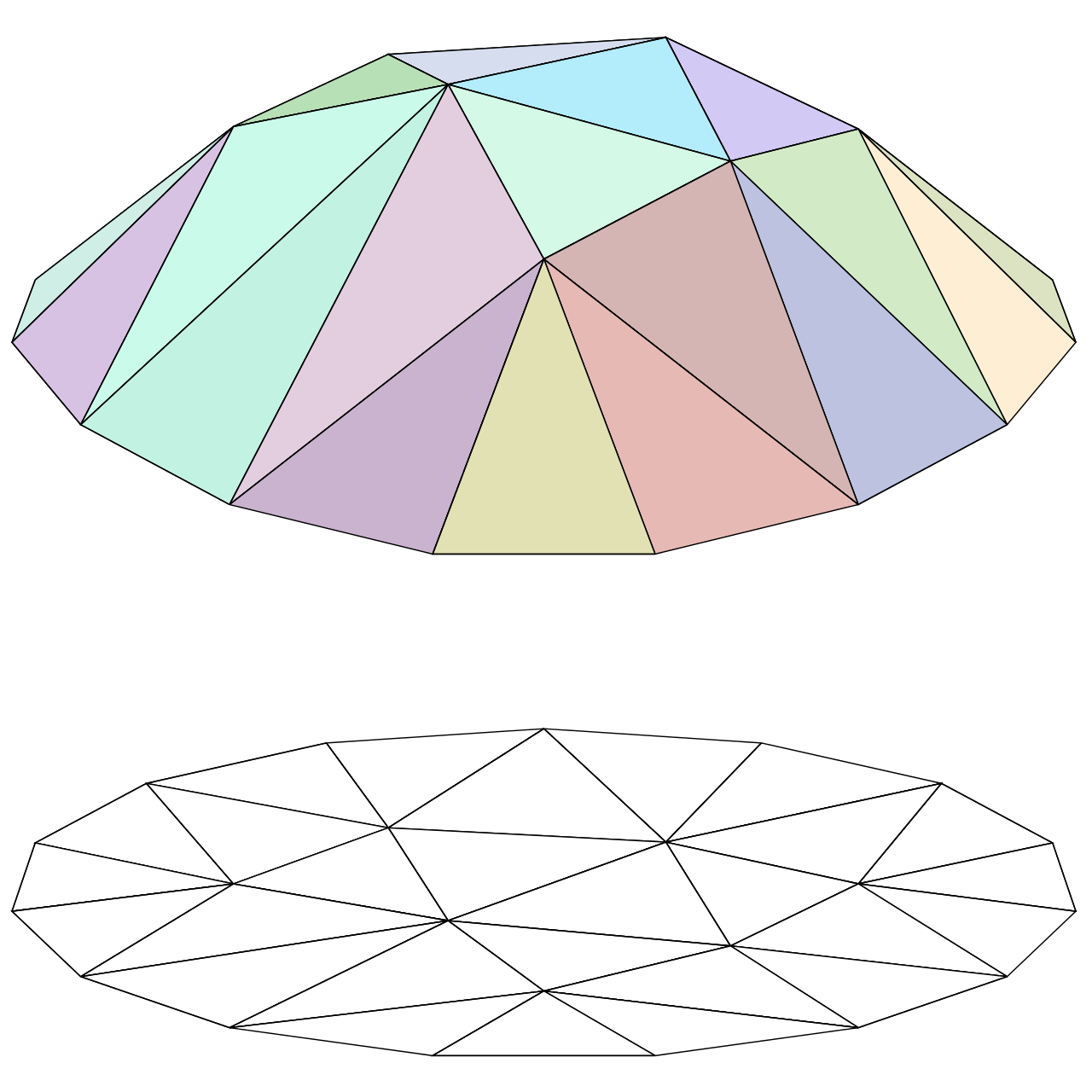
Ω. 在下图中,我们展示了一个 15 边多边形区域的三角剖分
Ω
{\displaystyle \Omega }
Ω在平面中(下图),以及该多边形的分段线性函数(上图,颜色),该函数在三角剖分的每个三角形上都是线性的;空间
V
{\displaystyle V}
V将由所选三角剖分的每个三角形上的线性函数组成。
人们希望随着底层三角形网格变得越来越精细,离散问题 (3) 的解在某种意义上会收敛到原始边值问题 P2 的解。为了测量这种网格细度,三角剖分由实值参数索引
h
>
0
{\displaystyle h>0}
h>0其中一个非常小。此参数将与三角剖分中最大或平均三角形的大小有关。当我们细化三角剖分时,分段线性函数的空间
V
{\displaystyle V}
V也必须改变
h
{\displaystyle h}
h. 出于这个原因,人们经常阅读
V
h
{\displaystyle V_{h}}
Vh代替
V
{\displaystyle V}
V在文献中。由于我们不进行这样的分析,我们不会使用这种表示法。
有限元法的一般形式
一般而言,有限元法的特征在于以下过程。
- 一个人选择一个网格 Ω {\displaystyle \Omega } Ω. 在前面的处理中,网格由三角形组成,但也可以使用正方形或曲线多边形。
- 然后,选择基函数。在我们的讨论中,我们使用了分段线性基函数,但使用分段多项式基函数也很常见。
单独考虑的是基函数的平滑度。对于二阶椭圆边值问题,仅连续的分段多项式基函数就足够了(即导数是不连续的)。对于高阶偏微分方程,必须使用更平滑的基函数。例如,对于一个四阶问题,例如
u
x
x
x
x
+
u
y
y
y
y
=
f
{\displaystyle u_{xxxx}+u_{yyyy}=f}
uxxxx+uyyyy=f,可以使用分段二次基函数
C
1
{\displaystyle C^{1}}
C1.
另一个考虑是有限维空间的关系
V
{\displaystyle V}
V在上面的例子中,它的无限维对应物
H
0
1
{\displaystyle H_{0}^{1}}
H01. 一致的元素方法是一种空间
V
{\displaystyle V}
V是连续问题的元素空间的子空间。上面的例子就是这样一种方法。如果不满足这个条件,我们就得到了一个非一致性单元法,其中一个例子是在每个边中点处连续的网格上的分段线性函数空间。由于这些函数通常沿边缘不连续,因此这个有限维空间不是原始的子空间
H
0
1
{\displaystyle H_{0}^{1}}
H01.
通常,有一种算法用于获取给定的网格并将其细分。如果提高精度的主要方法是细分网格,则有一个h方法(h通常是网格中最大元素的直径。)这样,如果一个网格显示误差
h
{\displaystyle h}
h上界为
C
h
p
{\displaystyle Ch^{p}}
Chp, 对于一些
C
<
∞
{\displaystyle C<\infty }
C<∞和
p
>
0
{\displaystyle p>0}
p>0,则有一个阶p方法。在某些假设下(例如,如果域是凸的),阶的分段多项式
d
{\displaystyle d}
d方法会有顺序错误
p
=
d
+
1
{\displaystyle p=d+1}
p=d+1.
如果不是使h更小,而是增加基函数中使用的多项式的次数,则可以使用p方法。如果将这两种细化类型结合起来,则会获得一种hp方法(hp-FEM)。在 hp-FEM 中,多项式次数可能因元素而异。具有较大均匀p的高阶方法称为谱有限元方法 ( SFEM )。不要将这些与光谱方法混淆。
对于向量偏微分方程,基函数可以取值
R
n
{\displaystyle \mathbb {R} ^{n}}
Rn.
各种类型的有限元方法
AEM
应用单元法或 AEM 结合了 FEM 和离散单元法或 (DEM) 的特征。
A-FEM
增广有限元法由 Yang 和 Lui 引入,他们的目标是模拟弱和强不连续性,而不需要像 PuM 所述的额外自由度。
广义有限元法
广义有限元法 (GFEM) 使用由函数组成的局部空间,不一定是多项式,它们反映了关于未知解的可用信息,从而确保了良好的局部近似。然后使用单位分区将这些空间“粘合”在一起以形成近似子空间。当应用于具有复杂边界的域问题、微尺度问题和边界层问题时,GFEM 的有效性已经得到证明。
混合有限元法
混合有限元法是一种在对偏微分方程问题进行离散化过程中引入额外的自变量作为节点变量的有限元方法。
变量 - 多项式
hp-FEM自适应地组合具有可变大小h和多项式次数p的元素,以实现异常快速的指数收敛速度。
hpk-FEM
hpk -FEM自适应地组合具有可变大小h的元素、局部近似p的多项式次数和局部近似(k-1)的全局可微性,以实现最佳收敛速度。
XFEM
扩展有限元法(XFEM) 是一种基于广义有限元法 (GFEM) 和单位分割法 (PUM) 的数值技术。它通过丰富具有不连续函数的微分方程的解的解空间来扩展经典有限元方法。扩展的有限元方法丰富了逼近空间,使其能够自然地再现与感兴趣的问题相关的具有挑战性的特征:不连续性、奇异性、边界层等。结果表明,对于某些问题,将问题的特征嵌入到逼近空间可以显着提高收敛速度和精度。此外,使用 XFEM 处理不连续性问题可以抑制对不连续性表面进行网格划分和重新划分网格的需要,
几个研究代码在不同程度上实现了这种技术:1. GetFEM++ 2. xfem++ 3. openxfem++
XFEM 也已在 Altair Radios、ASTER、Morfeo 和 Abaqus 等代码中实施。它越来越多地被其他商业有限元软件采用,提供一些插件和实际的核心实现(ANSYS、SAMCEF、OOFELIE 等)。
标度边界有限元法 (SBFEM)
缩放边界有限元法 (SBFEM) 的介绍来自 Song 和 Wolf (1997)。SBFEM 一直是断裂力学问题数值分析领域最有利可图的贡献之一。它是一种半解析基本无解方法,它结合了有限元公式和程序以及边界元离散化的优点。然而,与边界元法不同,它不需要基本微分解。
其他有限元法
S-FEM、谱元法、无网格方法、不连续 Galerkin 方法、有限元极限分析、拉伸网格法、Loubignac 迭代、晶体塑性有限元法 (CPFEM) 、虚元法 (VEM) 等等。
❤坚持读Paper,坚持做笔记,坚持学习,坚持刷力扣LeetCode❤!!!
坚持刷题!!!
⚡To Be No.1⚡⚡哈哈哈****哈
⚡创作不易⚡,过路能❤关注、收藏、点个赞❤三连就最好不过了
ღ( ´・ᴗ・` )
❤
版权归原作者 府学路18号车神 所有, 如有侵权,请联系我们删除。