一、导入数据
1.直接赋值

2.读取 Excel 文件
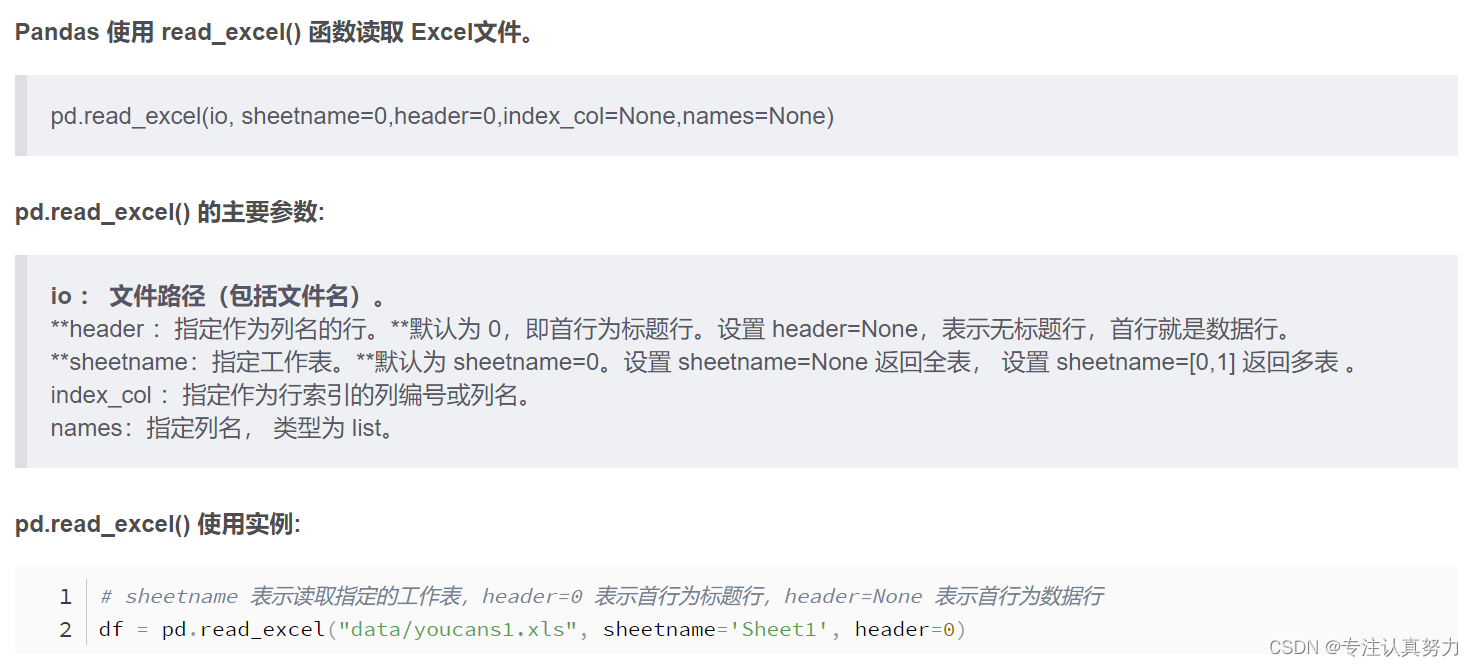
3.代码示例
import pandas as pd
# 读取数据文件defreadDataFile(readPath):# readPath: 数据文件的地址和文件名try:if(readPath[-4:]==".csv"):
dfFile = pd.read_csv(readPath, header=0, sep=",")# 间隔符为逗号,首行为标题行# dfFile = pd.read_csv(filePath, header=None, sep=",") # sep: 间隔符,无标题行elif(readPath[-4:]==".xls")or(readPath[-5:]==".xlsx"):# sheet_name 默认为 0
dfFile = pd.read_excel(readPath, header=0)# 首行为标题行# dfFile = pd.read_excel(filePath, header=None) # 无标题行elif(readPath[-4:]==".dat"):# sep: 间隔符,header:首行是否为标题行
dfFile = pd.read_table(readPath, sep=" ", header=0)# 间隔符为空格,首行为标题行# dfFile = pd.read_table(filePath,sep=",",header=None) # 间隔符为逗号,无标题行else:print("不支持的文件格式。")except Exception as e:print("读取数据文件失败:{}".format(str(e)))returnreturn dfFile
# 主程序defmain():# 读取数据文件
readPath ="../data/toothpaste.csv"# 数据文件的地址和文件名
dfFile = readDataFile(readPath)# 调用读取文件子程序print(type(dfFile))# 查看 dfFile 数据类型print(dfFile.shape)# 查看 dfFile 形状(行数,列数)print(dfFile.head())# 显示 dfFile 前 5 行数据returnif __name__ =='__main__':
main()
二、线性规划
1.什么是线性规划问题

2.线性规划问题如何求解
1.问题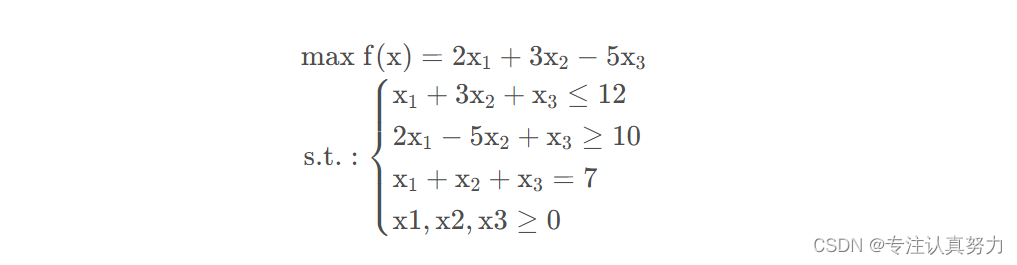
2.代码
import pulp # 导入 PuLP库函数# 1.定义一个规划问题
MyProbLP = pulp.LpProblem("LPProbDemo1", sense=pulp.LpMaximize)'''
pulp.LpProblem 是定义问题的构造函数。
"LPProbDemo1"是用户定义的问题名(用于输出信息)。
参数 sense 用来指定求最小值/最大值问题,可选参数值:LpMinimize、LpMaximize 。本例 “sense=pulp.LpMaximize” 表示求目标函数的最大值。
'''# 2.定义决策变量
x1 = pulp.LpVariable('x1', lowBound=0, upBound=7, cat='Continuous')
x2 = pulp.LpVariable('x2', lowBound=0, upBound=7, cat='Continuous')
x3 = pulp.LpVariable('x3', lowBound=0, upBound=7, cat='Continuous')'''
pulp.LpVariable 是定义决策变量的函数。
‘x1’ 是用户定义的变量名。
参数 lowBound、upBound 用来设定决策变量的下界、上界;可以不定义下界/上界,默认的下界/上界是负无穷/正无穷。本例中 x1,x2,x3 的取值区间为 [0,7]。
参数 cat 用来设定变量类型,可选参数值:‘Continuous’ 表示连续变量(默认值)、’ Integer ’ 表示离散变量(用于整数规划问题)、’ Binary ’ 表示0/1变量(用于0/1规划问题)。
'''# 3.设置目标函数
MyProbLP +=2* x1 +3* x2 -5* x3
'''
添加目标函数使用 “问题名 += 目标函数式” 格式。
'''# 4.添加约束条件
MyProbLP +=(2* x1 -5* x2 + x3 >=10)# 不等式约束
MyProbLP +=(x1 +3* x2 + x3 <=12)# 不等式约束
MyProbLP +=(x1 + x2 + x3 ==7)# 等式约束'''
添加约束条件使用 “问题名 += 约束条件表达式” 格式。
约束条件可以是等式约束或不等式约束,不等式约束可以是 小于等于 或 大于等于,分别使用关键字">="、"<=“和”=="。
'''# 5.求解
MyProbLP.solve()print("Status:", pulp.LpStatus[MyProbLP.status])# 输出求解状态for v in MyProbLP.variables():print(v.name,"=", v.varValue)# 输出每个变量的最优值print("F(x) = ", pulp.value(MyProbLP.objective))# 输出最优解的目标函数值'''
solve() 是求解函数。PuLP默认采用 CBC 求解器来求解优化问题,也可以调用其它的优化器来求解,如:GLPK,COIN CLP/CBC,CPLEX,和GUROBI,但需要另外安装。
'''
3.结果
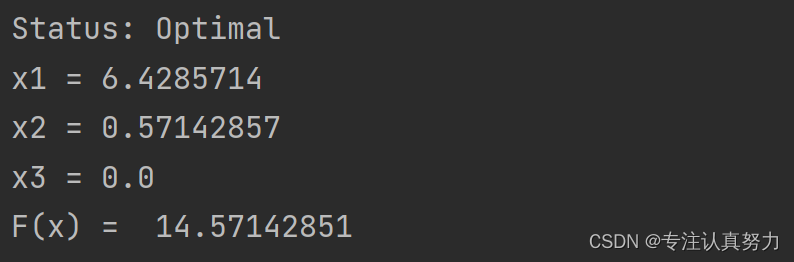
4.求解实例
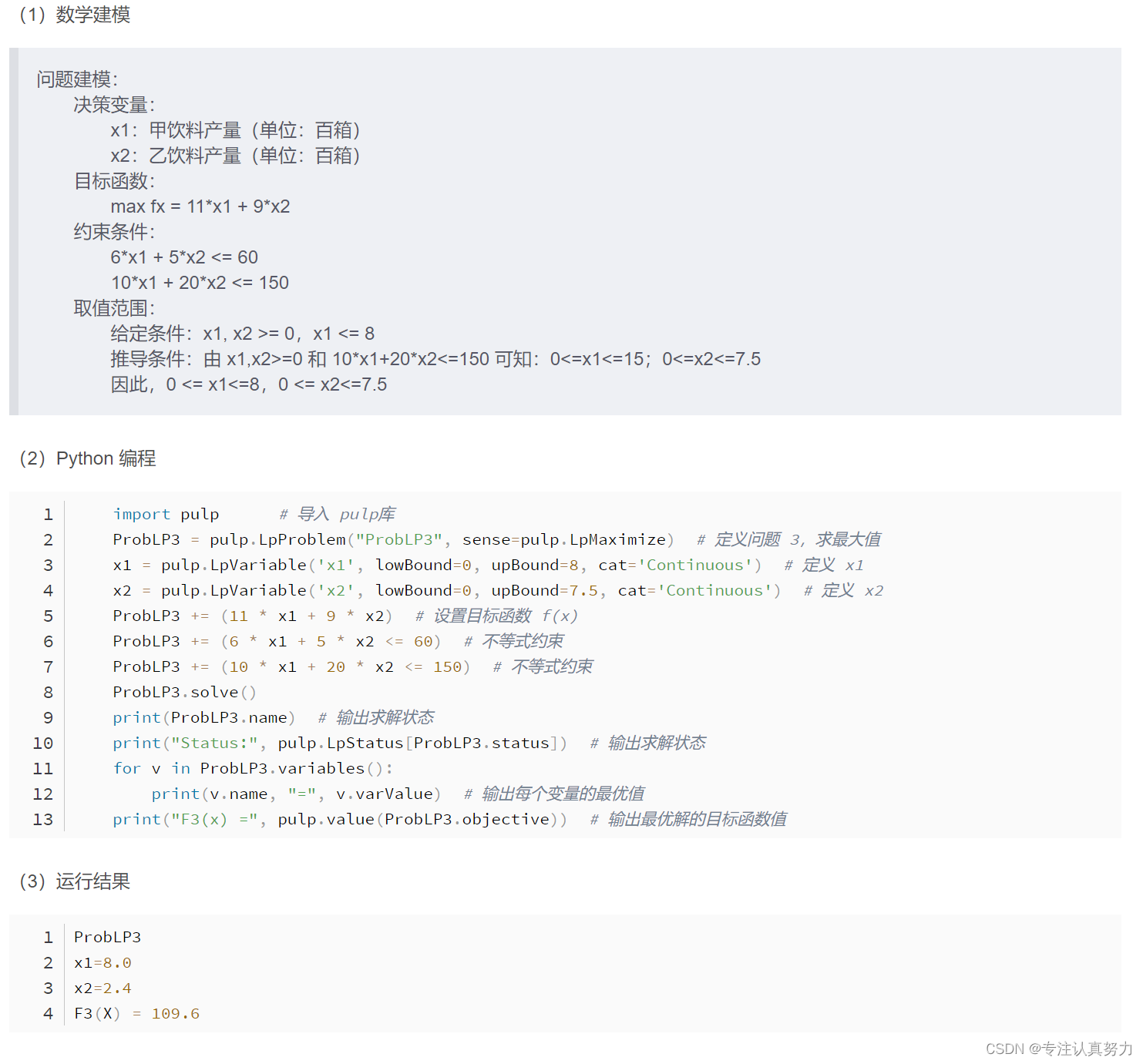
三、整数规划
线性规划问题的最优解可能是分数或小数。整数规划是指变量的取值只能是整数的规划。
pulp.LpVariable 用来定义决策变量的函数,参数 cat 用来设定变量类型,可选参数值:‘Continuous’ 表示连续变量(默认值)、’ Integer ’ 表示离散变量(用于整数规划问题)、’ Binary ’ 表示0/1变量(用于0/1规划问题)。
1.求解示例
import pulp # 导入 pulp 库# 主程序defmain():# 模型参数设置"""
问题描述:
某厂生产甲乙两种饮料,每百箱甲饮料需用原料6千克、工人10名,获利10万元;每百箱乙饮料需用原料5千克、工人20名,获利9万元。
今工厂共有原料60千克、工人150名,又由于其他条件所限甲饮料产量不超过8百箱。
(1)问如何安排生产计划,即两种饮料各生产多少使获利最大?
(2)若投资0.8万元可增加原料1千克,是否应作这项投资?投资多少合理?
(3)若不允许散箱(按整百箱生产),如何安排生产计划,即两种饮料各生产多少使获利最大?
(4)若不允许散箱(按整百箱生产),若投资0.8万元可增加原料1千克,是否应作这项投资?投资多少合理?
"""# 问题 1:"""
问题建模:
决策变量:
x1:甲饮料产量(单位:百箱)
x2:乙饮料产量(单位:百箱)
目标函数:
max fx = 10*x1 + 9*x2
约束条件:
6*x1 + 5*x2 <= 60
10*x1 + 20*x2 <= 150
x1, x2 >= 0,x1 <= 8
此外,由 x1,x2>=0 和 10*x1+20*x2<=150 可知 0<=x2<=7.5
"""
ProbLP1 = pulp.LpProblem("ProbLP1", sense=pulp.LpMaximize)# 定义问题 1,求最大值
x1 = pulp.LpVariable('x1', lowBound=0, upBound=8, cat='Continuous')# 定义 x1
x2 = pulp.LpVariable('x2', lowBound=0, upBound=7.5, cat='Continuous')# 定义 x2
ProbLP1 +=(10*x1 +9*x2)# 设置目标函数 f(x)
ProbLP1 +=(6*x1 +5*x2 <=60)# 不等式约束
ProbLP1 +=(10*x1 +20*x2 <=150)# 不等式约束
ProbLP1.solve()print(ProbLP1.name)# 输出求解状态print("Status :", pulp.LpStatus[ProbLP1.status])# 输出求解状态for v in ProbLP1.variables():print(v.name,"=", v.varValue)# 输出每个变量的最优值print("F1(x) =", pulp.value(ProbLP1.objective))# 输出最优解的目标函数值# 问题 2:"""
问题建模:
决策变量:
x1:甲饮料产量(单位:百箱)
x2:乙饮料产量(单位:百箱)
x3:增加投资(单位:万元)
目标函数:
max fx = 10*x1 + 9*x2 - x3
约束条件:
6*x1 + 5*x2 <= 60 + x3/0.8
10*x1 + 20*x2 <= 150
x1, x2, x3 >= 0,x1 <= 8
此外,由 x1,x2>=0 和 10*x1+20*x2<=150 可知 0<=x2<=7.5
"""
ProbLP2 = pulp.LpProblem("ProbLP2", sense=pulp.LpMaximize)# 定义问题 2,求最大值
x1 = pulp.LpVariable('x1', lowBound=0, upBound=8, cat='Continuous')# 定义 x1
x2 = pulp.LpVariable('x2', lowBound=0, upBound=7.5, cat='Continuous')# 定义 x2
x3 = pulp.LpVariable('x3', lowBound=0, cat='Continuous')# 定义 x3
ProbLP2 +=(10*x1 +9*x2 - x3)# 设置目标函数 f(x)
ProbLP2 +=(6*x1 +5*x2 -1.25*x3 <=60)# 不等式约束
ProbLP2 +=(10*x1 +20*x2 <=150)# 不等式约束
ProbLP2.solve()print(ProbLP2.name)# 输出求解状态print("Status :", pulp.LpStatus[ProbLP2.status])# 输出求解状态for v in ProbLP2.variables():print(v.name,"=", v.varValue)# 输出每个变量的最优值print("F2(x) =", pulp.value(ProbLP2.objective))# 输出最优解的目标函数值# 问题 3:整数规划问题"""
问题建模:
决策变量:
x1:甲饮料产量,正整数(单位:百箱)
x2:乙饮料产量,正整数(单位:百箱)
目标函数:
max fx = 10*x1 + 9*x2
约束条件:
6*x1 + 5*x2 <= 60
10*x1 + 20*x2 <= 150
x1, x2 >= 0,x1 <= 8,x1, x2 为整数
此外,由 x1,x2>=0 和 10*x1+20*x2<=150 可知 0<=x2<=7.5
"""
ProbLP3 = pulp.LpProblem("ProbLP3", sense=pulp.LpMaximize)# 定义问题 3,求最大值print(ProbLP3.name)# 输出求解状态
x1 = pulp.LpVariable('x1', lowBound=0, upBound=8, cat='Integer')# 定义 x1,变量类型:整数
x2 = pulp.LpVariable('x2', lowBound=0, upBound=7.5, cat='Integer')# 定义 x2,变量类型:整数
ProbLP3 +=(10* x1 +9* x2)# 设置目标函数 f(x)
ProbLP3 +=(6* x1 +5* x2 <=60)# 不等式约束
ProbLP3 +=(10* x1 +20* x2 <=150)# 不等式约束
ProbLP3.solve()print("Status:", pulp.LpStatus[ProbLP3.status])# 输出求解状态for v in ProbLP3.variables():print(v.name,"=", v.varValue)# 输出每个变量的最优值print("F3(x) =", pulp.value(ProbLP3.objective))# 输出最优解的目标函数值# 问题 4:"""
问题建模:
决策变量:
x1:甲饮料产量,正整数(单位:百箱)
x2:乙饮料产量,正整数(单位:百箱)
x3:增加投资(单位:万元)
目标函数:
max fx = 10*x1 + 9*x2 - x3
约束条件:
6*x1 + 5*x2 <= 60 + x3/0.8
10*x1 + 20*x2 <= 150
x1, x2, x3 >= 0,x1 <= 8,x1, x2 为整数
此外,由 x1,x2>=0 和 10*x1+20*x2<=150 可知 0<=x2<=7.5
"""
ProbLP4 = pulp.LpProblem("ProbLP4", sense=pulp.LpMaximize)# 定义问题 4,求最大值print(ProbLP4.name)# 输出求解状态
x1 = pulp.LpVariable('x1', lowBound=0, upBound=8, cat='Integer')# 定义 x1,变量类型:整数
x2 = pulp.LpVariable('x2', lowBound=0, upBound=7, cat='Integer')# 定义 x2,变量类型:整数
x3 = pulp.LpVariable('x3', lowBound=0, cat='Continuous')# 定义 x3
ProbLP4 +=(10*x1 +9*x2 - x3)# 设置目标函数 f(x)
ProbLP4 +=(6*x1 +5*x2 -1.25*x3 <=60)# 不等式约束
ProbLP4 +=(10*x1 +20*x2 <=150)# 不等式约束
ProbLP4.solve()print("Status:", pulp.LpStatus[ProbLP4.status])# 输出求解状态for v in ProbLP4.variables():print(v.name,"=", v.varValue)# 输出每个变量的最优值print("F4(x) =", pulp.value(ProbLP4.objective))# 输出最优解的目标函数值returnif __name__ =='__main__':
main()
2.结果




四、0-1规划
0-1 整数规划是一类特殊的整数规划,变量的取值只能是 0 或 1。主要用于求解互斥的决策问题、互斥的约束条件问题、固定费用问题和分派问题。
1.规划的分类及建模方法
规划问题的数学模型包括决策变量、约束条件和目标函数,围绕这三个要素都可能存在互斥的情况,从而导出不同类型的0-1规划问题,其建模方法也有差别。
- 1.互斥的决策问题

- 2.互斥的约束问题

- 3.固定费用问题

- 4.指派问题

2.PuLP 求解 0-1 规划问题
1.案例问题描述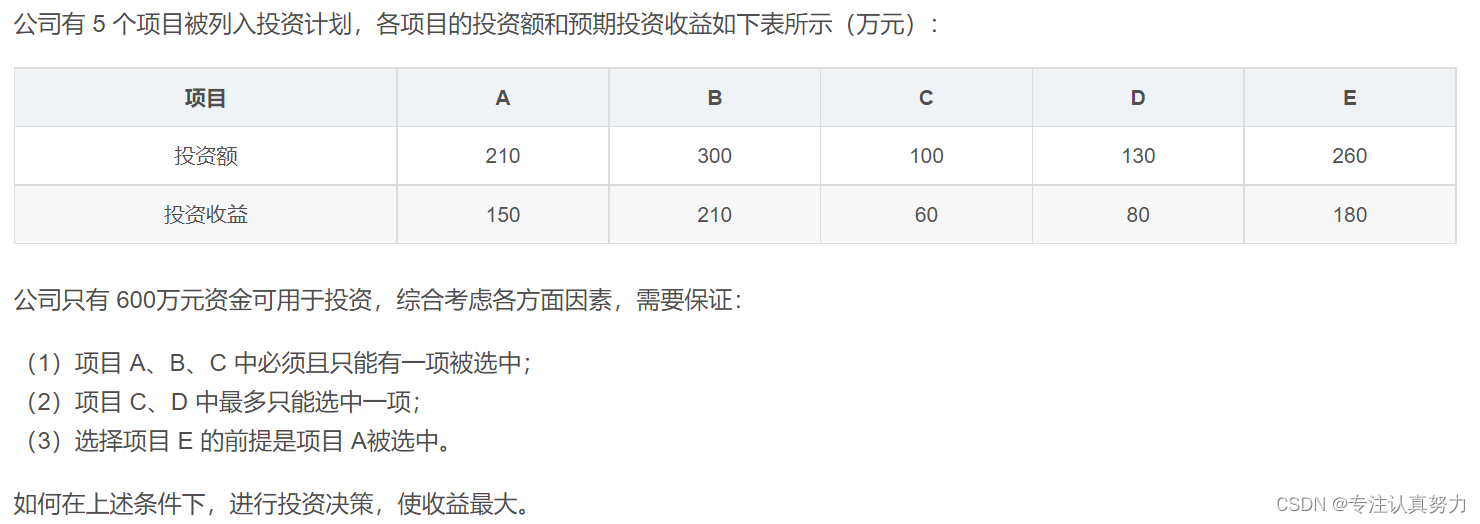
2.建模过程分析
3.模型求解的编程
import pulp # 导入 pulp 库# 主程序defmain():# 投资决策问题:# 公司现有 5个拟投资项目,根据投资额、投资收益和限制条件,问如何决策使收益最大。"""
问题建模:
决策变量:
x1~x5:0/1 变量,1 表示选择第 i 个项目, 0 表示不选择第 i 个项目
目标函数:
max fx = 150*x1 + 210*x2 + 60*x3 + 80*x4 + 180*x5
约束条件:
210*x1 + 300*x2 + 100*x3 + 130*x4 + 260*x5 <= 600
x1 + x2 + x3 = 1
x3 + x4 <= 1
x5 <= x1
x1,...,x5 = 0, 1
"""
InvestLP = pulp.LpProblem("Invest decision problem", sense=pulp.LpMaximize)# 定义问题,求最大值# 参数 cat 用来设定变量类型,’ Binary ’ 表示0/1变量(用于0/1规划问题)。
x1 = pulp.LpVariable('A', cat='Binary')# 定义 x1,A 项目
x2 = pulp.LpVariable('B', cat='Binary')# 定义 x2,B 项目
x3 = pulp.LpVariable('C', cat='Binary')# 定义 x3,C 项目
x4 = pulp.LpVariable('D', cat='Binary')# 定义 x4,D 项目
x5 = pulp.LpVariable('E', cat='Binary')# 定义 x5,E 项目
InvestLP +=(150*x1 +210*x2 +60*x3 +80*x4 +180*x5)# 设置目标函数 f(x)
InvestLP +=(210*x1 +300*x2 +100*x3 +130*x4 +260*x5 <=600)# 不等式约束
InvestLP +=(x1 + x2 + x3 ==1)# 等式约束
InvestLP +=(x3 + x4 <=1)# 不等式约束
InvestLP +=(x5 - x1 <=0)# 不等式约束
InvestLP.solve()# solve() 是求解函数,可以对求解器、求解精度进行设置。print(InvestLP.name)# 输出求解状态print("Status youcans:", pulp.LpStatus[InvestLP.status])# 输出求解状态for v in InvestLP.variables():print(v.name,"=", v.varValue)# 输出每个变量的最优值print("Max f(x) =", pulp.value(InvestLP.objective))# 输出最优解的目标函数值returnif __name__ =='__main__':
main()
4.运行结果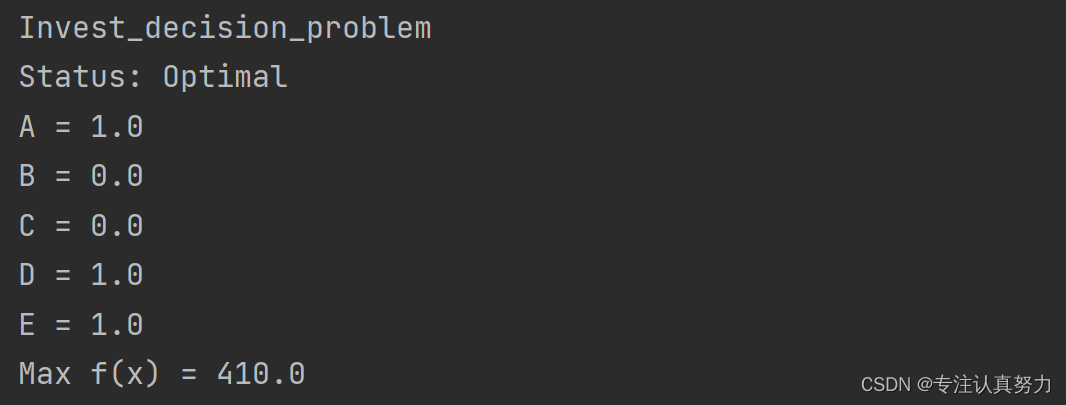
结论:从 0-1 规划模型的结果可知,选择 A、C、E 项目进行投资,可以满足限定条件并获得最大收益 410万元。
五、固定费用问题
1.问题定义

2.案例
1.问题描述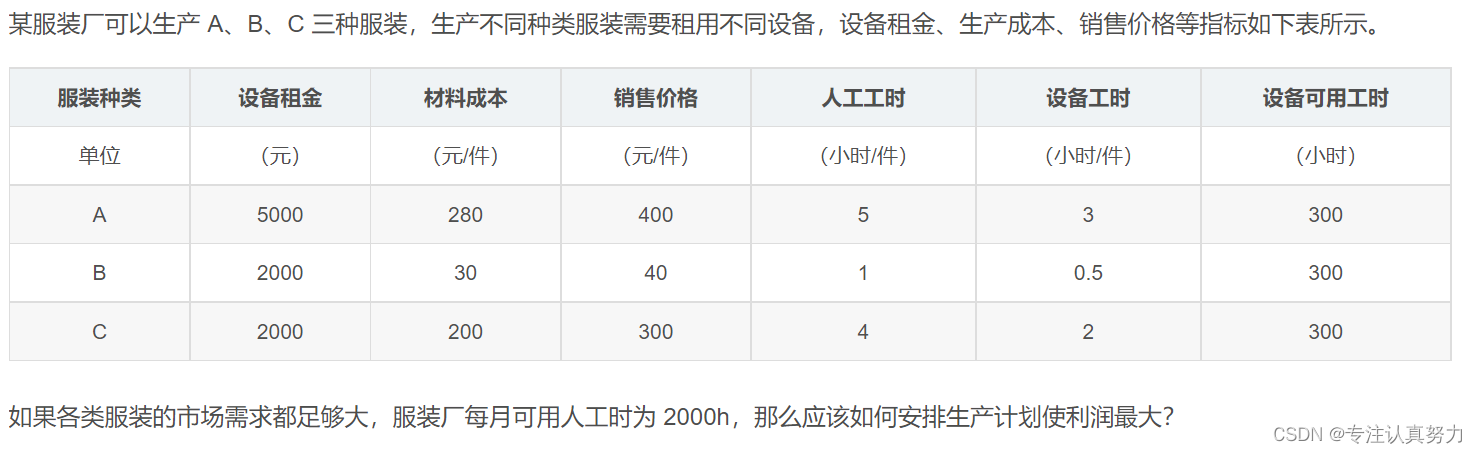
2.建模分析
首先要理解生产某种服装就会发生设备租金,租金只与是否生产该产品有关,而与生产数量无关,这就是固定成本。因此本题属于固定费用问题。
有些同学下意识地认为是从 3 种产品中选择一种,但题目中并没有限定必须或只能生产一种产品,因此决策结果可以是都不生产、选择 1 种或 2 种产品、3 种都生产。
3.编程求解
import pulp # 导入 pulp 库# 主程序defmain():# 固定费用问题(Fixed cost problem)print("固定费用问题(Fixed cost problem)")# 问题建模:"""
决策变量:
y(i) = 0, 不生产第 i 种产品
y(i) = 1, 生产第 i 种产品
x(i), 生产第 i 种产品的数量, i>=0 整数
i=1,2,3
目标函数:
min profit = 120x1 + 10x2+ 100x3 - 5000y1 - 2000y2 - 2000y3
约束条件:
5x1 + x2 + 4x3 <= 2000
3x1 <= 300y1
0.5x2 <= 300y2
2x3 <= 300y3
变量取值范围:
0<=x1<=100, 0<=x2<=600, 0<=x3<=150, 整数变量
y1, y2 ,y3 为 0/1 变量
"""# 1. 固定费用问题(Fixed cost problem), 使用 PuLP 工具包求解# (1) 建立优化问题 FixedCostP1: 求最大值(LpMaximize)
FixedCostP1 = pulp.LpProblem("Fixed_cost_problem_1", sense=pulp.LpMaximize)# 定义问题,求最大值# (2) 建立变量
x1 = pulp.LpVariable('A', cat='Binary')# 定义 x1,0-1变量,是否生产 A 产品
x2 = pulp.LpVariable('B', cat='Binary')# 定义 x2,0-1变量,是否生产 B 产品
x3 = pulp.LpVariable('C', cat='Binary')# 定义 x3,0-1变量,是否生产 C 产品
y1 = pulp.LpVariable('yieldA', lowBound=0, upBound=100, cat='Integer')# 定义 y1,整型变量
y2 = pulp.LpVariable('yieldB', lowBound=0, upBound=600, cat='Integer')# 定义 y2,整型变量
y3 = pulp.LpVariable('yieldC', lowBound=0, upBound=150, cat='Integer')# 定义 y3,整型变量# (3) 设置目标函数
FixedCostP1 += pulp.lpSum(-5000*x1-2000*x2-2000*x3+120*y1+10*y2+100*y3)# 设置目标函数 f(x)# (4) 设置约束条件
FixedCostP1 +=(5*y1 + y2 +4*y3 <=2000)# 不等式约束
FixedCostP1 +=(3*y1 -300*x1 <=0)# 不等式约束
FixedCostP1 +=(0.5*y2 -300*x2 <=0)# 不等式约束
FixedCostP1 +=(2*y3 -300*x3 <=0)# 不等式约束# (5) 求解
FixedCostP1.solve()# (6) 打印结果print(FixedCostP1.name)if pulp.LpStatus[FixedCostP1.status]=="Optimal":# 获得最优解for v in FixedCostP1.variables():print(v.name,"=", v.varValue)# 输出每个变量的最优值print("F(x) = ", pulp.value(FixedCostP1.objective))# 输出最优解的目标函数值returnif __name__ =='__main__':
main()
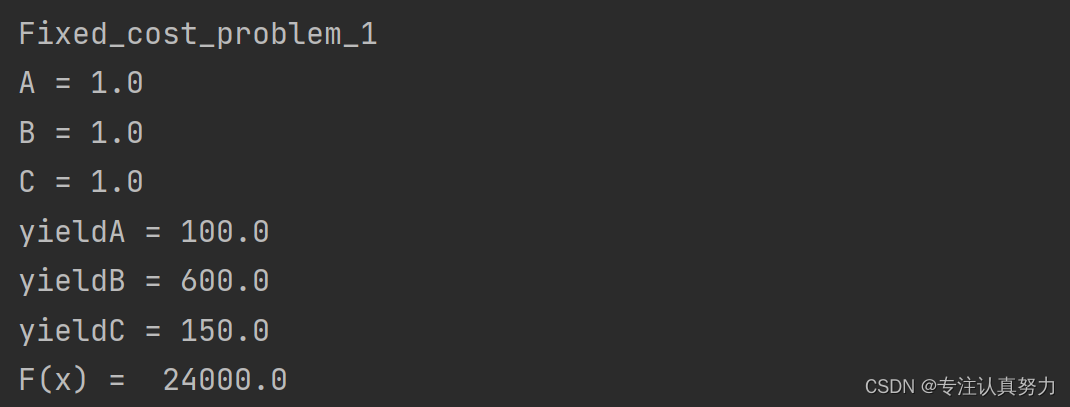
结论:从固定费用问题模型的求解结果可知,A、B、C 三种服装都生产,产量分别为 A/100、B/600、C/150 时获得最大利润为:24000。
4.字典格式快捷建模方法
import pulp # 导入 pulp 库# 主程序defmain():# 2. 问题同上,PuLP 快捷方法示例# (1) 建立优化问题 FixedCostP2: 求最大值(LpMaximize)
FixedCostP2 = pulp.LpProblem("Fixed_cost_problem_2", sense=pulp.LpMaximize)# 定义问题,求最大值# (2) 建立变量
types =['A','B','C']# 定义产品种类
status = pulp.LpVariable.dicts("生产决策", types, cat='Binary')# 定义 0/1 变量,是否生产该产品
yields = pulp.LpVariable.dicts("生产数量", types, lowBound=0, upBound=600, cat='Integer')# 定义整型变量# (3) 设置目标函数
fixedCost ={'A':5000,'B':2000,'C':2000}# 各产品的 固定费用
unitProfit ={'A':120,'B':10,'C':100}# 各产品的 单位利润
FixedCostP2 += pulp.lpSum([(yields[i]* unitProfit[i]- status[i]* fixedCost[i])for i in types])# (4) 设置约束条件
humanHours ={'A':5,'B':1,'C':4}# 各产品的 单位人工工时
machineHours ={'A':3.0,'B':0.5,'C':2.0}# 各产品的 单位设备工时
maxHours ={'A':300,'B':300,'C':300}# 各产品的 最大设备工时
FixedCostP2 += pulp.lpSum([humanHours[i]* yields[i]for i in types])<=2000# 不等式约束for i in types:
FixedCostP2 +=(yields[i]* machineHours[i]- status[i]* maxHours[i]<=0)# 不等式约束# (5) 求解
FixedCostP2.solve()# (6) 打印结果print(FixedCostP2.name)
temple ="品种 %(type)s 的决策是:%(status)s,生产数量为:%(yields)d"if pulp.LpStatus[FixedCostP2.status]=="Optimal":# 获得最优解for i in types:
output ={'type': i,'status':'同意'if status[i].varValue else'否决','yields': yields[i].varValue}print(temple % output)print("最大利润 = ", pulp.value(FixedCostP2.objective))# 输出最优解的目标函数值returnif __name__ =='__main__':
main()

六、选址问题
选址问题是指在某个区域内选择设施的位置使所需的目标达到最优。选址问题也是一种互斥的计划问题。
选址问题有四个基本要素:设施、区域、距离和优化目标。
1.P-中位问题

2.P-中心问题

3.集合覆盖问题

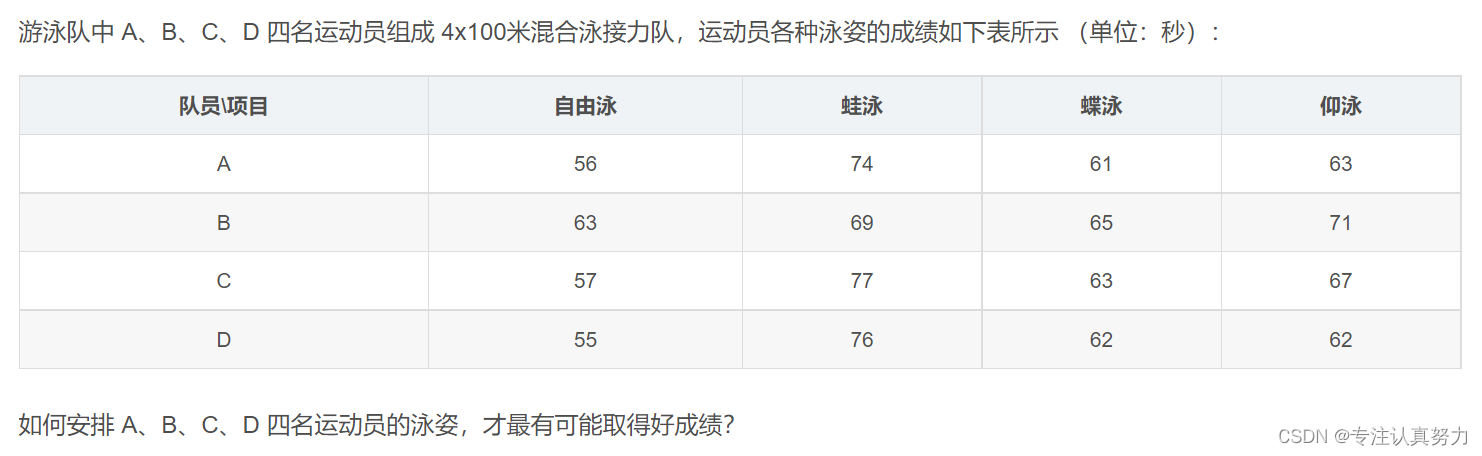
4.游泳接力赛的指派问题


import pulp # 导入 pulp 库import numpy as np
# 主程序defmain():# 问题建模:"""
决策变量:
x(i,j) = 0, 第 i 个人不游第 j 种姿势
x(i,j) = 1, 第 i 个人游第 j 种姿势
i=1,4, j=1,4
目标函数:
min time = sum(sum(c(i,j)*x(i,j))), i=1,4, j=1,4
约束条件:
sum(x(i,j),j=1,4)=1, i=1,4
sum(x(i,j),i=1,4)=1, j=1,4
变量取值范围:
x(i,j) = 0,1
"""# 游泳比赛的指派问题 (assignment problem)# 1.建立优化问题 AssignLP: 求最小值(LpMinimize)
AssignLP = pulp.LpProblem("Assignment_problem_for_swimming_relay_race", sense=pulp.LpMinimize)# 定义问题,求最小值# 2. 建立变量
rows = cols =range(0,4)
x = pulp.LpVariable.dicts("x",(rows, cols), cat="Binary")# 3. 设置目标函数
scoreM =[[56,74,61,63],[63,69,65,71],[57,77,63,67],[55,76,62,62]]
AssignLP += pulp.lpSum([[x[row][col]*scoreM[row][col]for row in rows]for col in cols])# 4. 施加约束for row in rows:
AssignLP += pulp.lpSum([x[row][col]for col in cols])==1# sum(x(i,j),j=1,4)=1, i=1,4for col in cols:
AssignLP += pulp.lpSum([x[row][col]for row in rows])==1# sum(x(i,j),i=1,4)=1, j=1,4# 5. 求解
AssignLP.solve()# 6. 打印结果print(AssignLP.name)
member =["队员A","队员B","队员C","队员D"]
style =["自由泳","蛙泳","蝶泳","仰泳"]if pulp.LpStatus[AssignLP.status]=="Optimal":# 获得最优解
xValue =[v.varValue for v in AssignLP.variables()]# [0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0]
xOpt = np.array(xValue).reshape((4,4))# 将 xValue 格式转换为 4x4 矩阵print("最佳分配:")for row in rows:print("{}\t{} 参加项目:{}".format(xOpt[row],member[row],style[np.argmax(xOpt[row])]))print("预测最好成绩为:{}".format(pulp.value(AssignLP.objective)))returnif __name__ =='__main__':
main()

5.消防站的选址问题
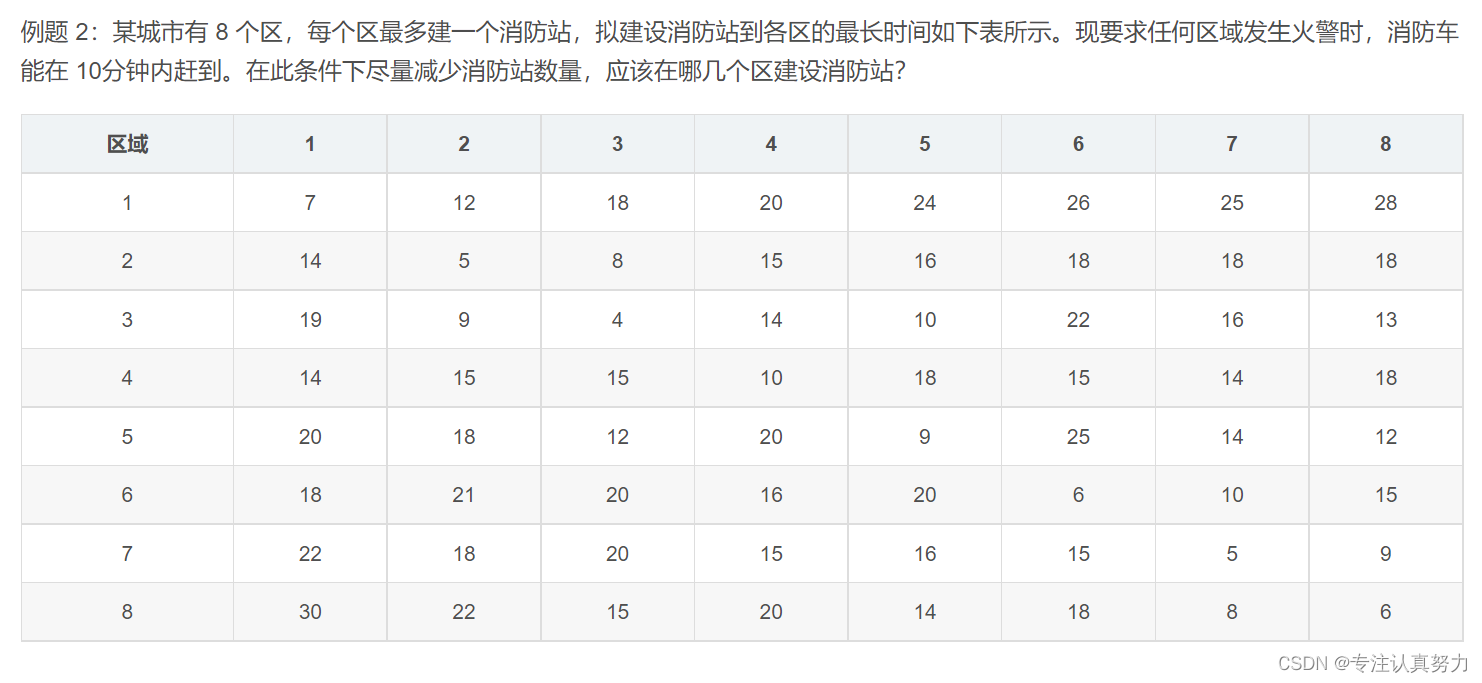
import pulp # 导入 pulp 库# 主程序defmain():# 问题建模:"""
决策变量:
x(j) = 0, 不选择第 j 个消防站
x(j) = 1, 选择第 j 个消防站, j=1,8
目标函数:
min fx = sum(x(j)), j=1,8
约束条件:
sum(x(j)*R(i,j),j=1,8) >=1, i=1,8
变量取值范围:
x(j) = 0,1
"""# 消防站的选址问题 (set covering problem, site selection of fire station)# 1.建立优化问题 SetCoverLP: 求最小值(LpMinimize)
SetCoverLP = pulp.LpProblem("SetCover_problem_for_fire_station", sense=pulp.LpMinimize)# 定义问题,求最小值# 2. 建立变量
zones =list(range(8))# 定义各区域
x = pulp.LpVariable.dicts("zone", zones, cat="Binary")# 定义 0/1 变量,是否在该区域设消防站# 3. 设置目标函数
SetCoverLP += pulp.lpSum([x[j]for j inrange(8)])# 设置消防站的个数# 4. 施加约束
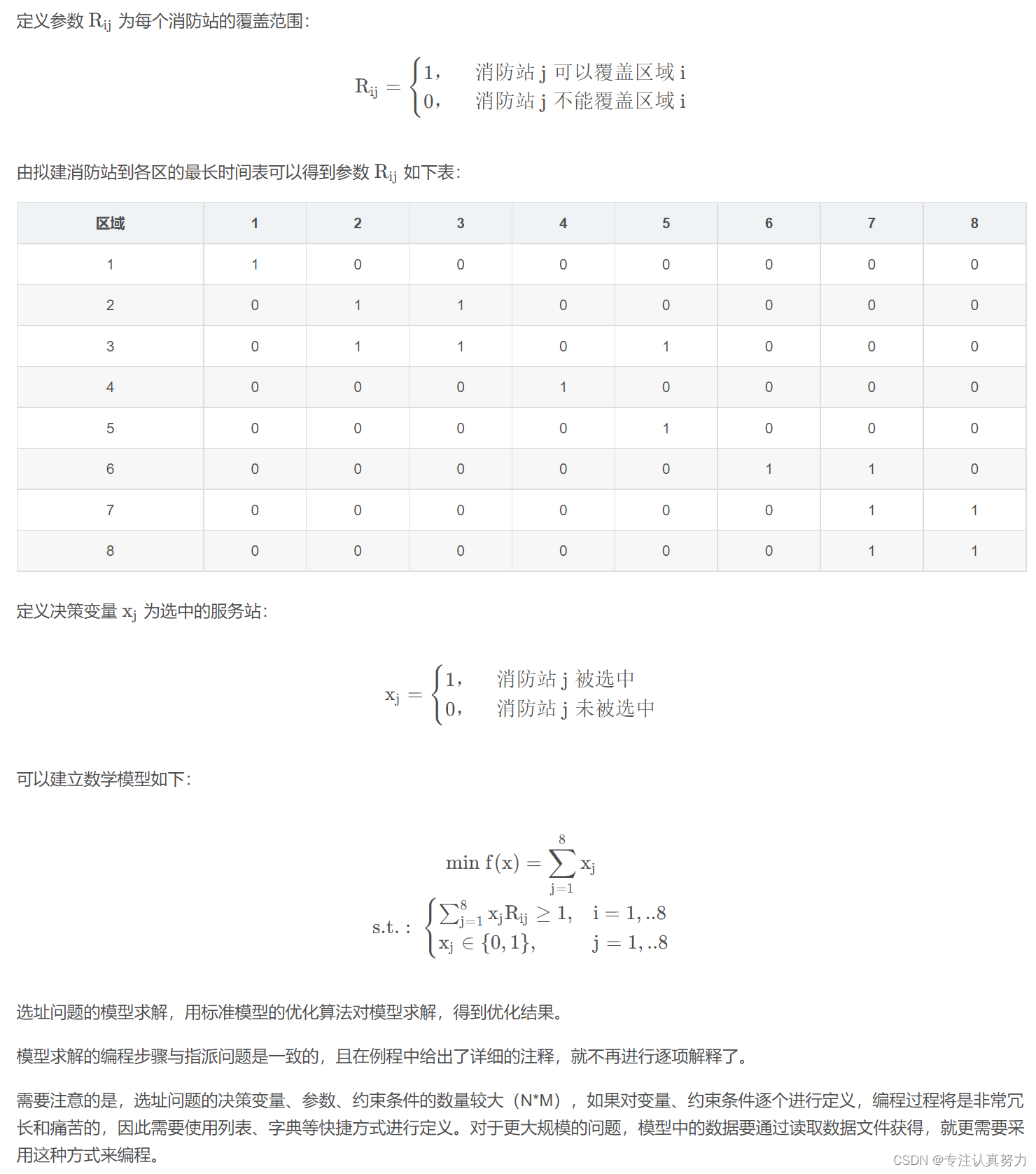
reachable =[[1,0,0,0,0,0,0,0],[0,1,1,0,0,0,0,0],[0,1,1,0,1,0,0,0],[0,0,0,1,0,0,0,0],[0,0,0,0,1,0,0,0],[0,0,0,0,0,1,1,0],[0,0,0,0,0,0,1,1],[0,0,0,0,0,0,1,1]]# 参数矩阵,第 i 消防站能否在 10分钟内到达第 j 区域for i inrange(8):
SetCoverLP += pulp.lpSum([x[j]* reachable[j][i]for j inrange(8)])>=1# 5. 求解
SetCoverLP.solve()# 6. 打印结果print(SetCoverLP.name)
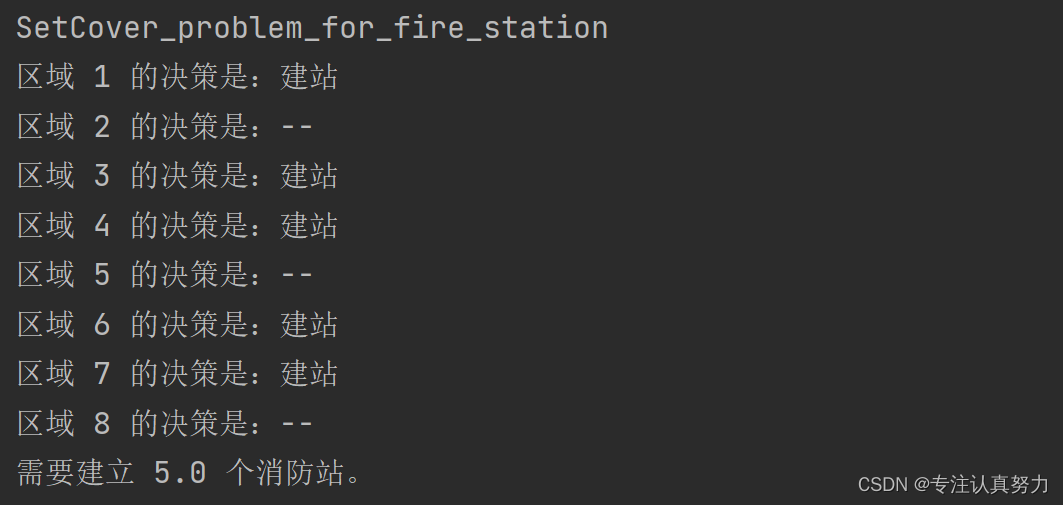
temple ="区域 %(zone)d 的决策是:%(status)s"# 格式化输出if pulp.LpStatus[SetCoverLP.status]=="Optimal":# 获得最优解for i inrange(8):
output ={'zone': i +1,# 与问题中区域 1~8 一致'status':'建站'if x[i].varValue else'--'}print(temple % output)print("需要建立 {} 个消防站。".format(pulp.value(SetCoverLP.objective)))returnif __name__ =='__main__':
main()
版权归原作者 专注认真努力 所有, 如有侵权,请联系我们删除。