最小平方误差算法

1．1 题目的主要研究内容

（1）用LMSE算法求下列模式分类的解向量w

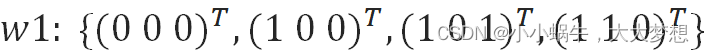
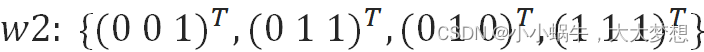
（2）制造PPT，并讲解。

1．2 题目研究的工作基础

1.2.1 LMSE算法步骤：

（1）根据N个分属于两类的样本，写出规范化增广样本矩阵X；

（2）求X的伪逆矩阵X#=(XTX)-1XT;

（3）设置初值c和B(1)，c为正的校正增量，B(1)的各分量大于零，迭代次数k=1。

开始迭代：计算

（4）计算𝒆(𝒌)=𝑿𝑾(𝒌)−𝑩(𝒌)，进行可分性判别。

如果e(k)=0，线性可分，解为W(k)，算法结束；

如果e(k)>0，线性可分，若进入（5）可使𝒆(𝒌)→𝟎，得最优解；

如果e(k)<0，线性不可分，停止迭代，无解，算法结束。

否则，说明e(k)的各分量值有正有负，进入（5）。

（5）计算W(K+1)和B(K+1)。

方法1：分别计算𝑊(𝑘+1)=𝑊(𝑘)+𝑐𝑋#|𝑒(𝑘)|

           𝐵(𝑘+1)=𝐵(𝑘)+𝑐[𝑒(𝑘)+|𝑒(𝑘)|]

方法2：先计算𝐵(𝑘+1)=𝐵(𝑘)+𝑐[𝑒(𝑘)+|𝑒(𝑘)|]

           再计算𝑊(𝑘+1)=𝑋#𝐵(𝑘+1)

迭代次数k加1，返回（4）

1.2.2 向量的范数：

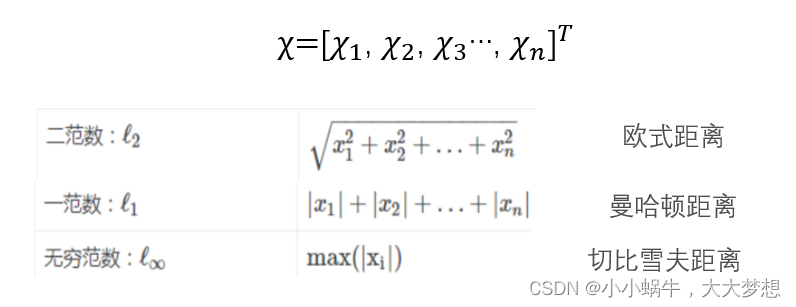
    我们利用向量的范数，对迭代停止的条件进行判断，这三种范数都是可以的。下面手动推演和程序实现均采用二范数，即欧式范数对迭代是否停止进行判断。

1．3 手动推演

1．4 流程图

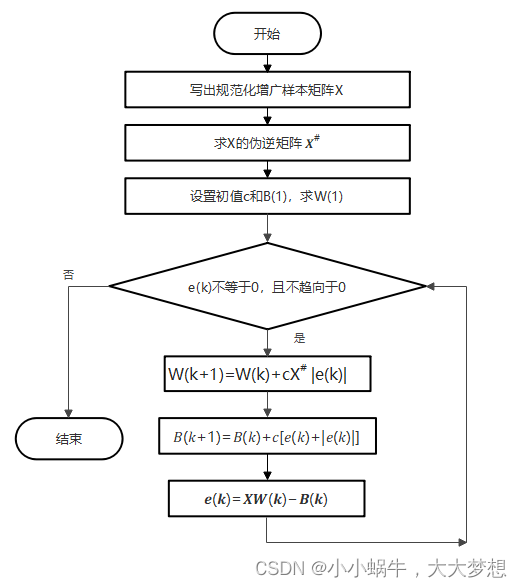
1．5 主要程序代码

（1）Python代码实现

import numpy as np
def simm(e):
    L=len(e)
    flag=0
    s=0
    for k in e:
        if(k<0):
            s+=1
    if s==L:
        flag=1
    return flag
"步骤一：规范化样本增广矩阵"
w1 = np.array([[0, 0,1], [1,1,1]])
w2 = np.array([[0,-1,-1], [-1,0,-1]])
"步骤二，求伪逆矩阵"
X = np.concatenate((w1, w2), axis=0) #将两个矩阵合并在一起
#print(X)
wn=np.matmul(np.linalg.inv(np.matmul(X.transpose(), X)), X.transpose())#伪逆矩阵
"步骤三，设置初始值，求w1"
b = np.array([1,1,1,1])
c = 1
w = np.matmul(wn,b)
#w1
e = np.matmul(X,w) - b
"步骤四，步骤五，循环，判别"
i=0
if simm(e)==1:
  print('线性不可分')
elif np.linalg.norm(e) > 0:
    while np.linalg.norm(e) > 0.001:
        dkh = e + abs(e)
        b = b + c * dkh
        w = w + c * np.matmul(wn, dkh)
        e = np.matmul(X, w) - b
        if simm(e) == 1:
            print('线性不可分')
        i += 1
print(wn, '\n','\n', w, '\n','\n', e)
elif np.linalg.norm(e) == 0:
    print('线性可分，解出w，算法结束')
print("第%d次迭代满足条件"%i)

（2）Matlab代码实现

%规范化增广样本矩阵
x=[0 0 0 1;1 0 0 1;1 0 1 1;1 1 0 1;0 0 -1 -1;0 -1 -1 -1;0 -1 0 -1;-1 -1 -1 -1];
B=[1;1;1;1;1;1;1;1];%设置B(1)的初值
C=1;%计算C的初值
%求x的伪逆矩阵
x1=inv(x'*x);%计算x的转置乘以x然后求逆矩阵，结果为x1
xh=x1*x';%x1乘以x的转置得到xh，也就是x的伪逆矩阵
%求w1
w = xh*B;
e = x*w - B;%计算e(1)
disp(w);%输出数组w
%对e(k)进行判别
i=1;
while(norm(e)>0.01)
     if e<0
         fprintf('线性不可分无解');
         break;
     end
     if e==0
         fprintf('线性可分');
         break;
     end
     w=w+C*xh*abs(e);
     B=B+C*(e+abs(e));
     e=x*w-B;
     i=i+1;
     fprintf('第%i次迭代的结果w:\n',i);
     disp(w);
end

1．6 运行结果及分析

（1）Python代码结果

（2）Matlab代码结果

（3）手动推演的结果

    三种实现方式都近似得到： 𝑑(𝑥)=2𝑥1−2𝑥2−2𝑥3+1

    故该题目的判别函数为𝑑(𝑥)=2𝑥1−2𝑥2−2𝑥3+1，两类的分界面为2𝑥1−2𝑥2−2𝑥3+1=0。将第一类的点带入判别公式，得到的值都大于0，将第二类的点带入判别公式，得到的值都小于0。