熟悉一下汉诺塔
python解决汉诺塔问题
问题:
有三个立柱A、B、C。A柱上穿有大小不等的圆盘N个,较大的圆盘在下,较小的圆盘在上。要求把A柱上的圆盘全部移到C柱上,保持大盘在下、小盘在上的规律(可借助B柱)。每次移动只能把一个柱子最上面的圆盘移到另一个柱子的最上面。请输出移动过程。
问题分析(看图):
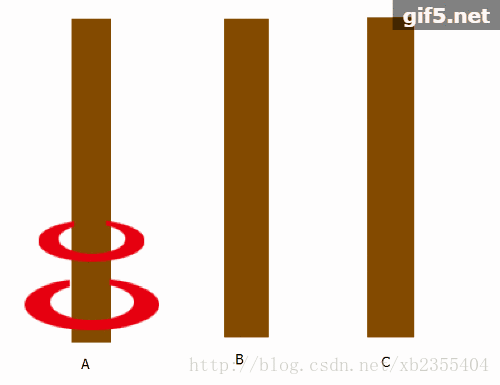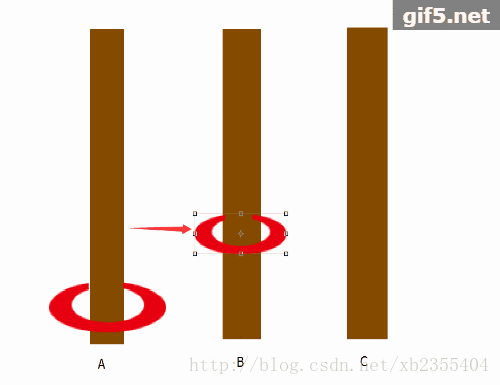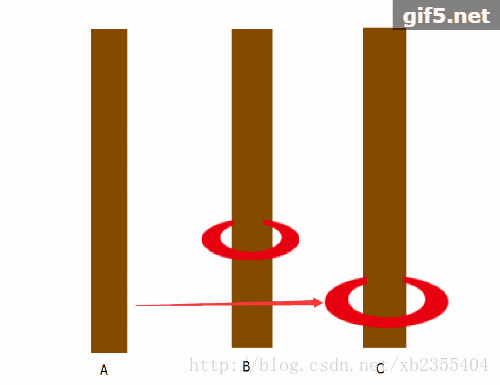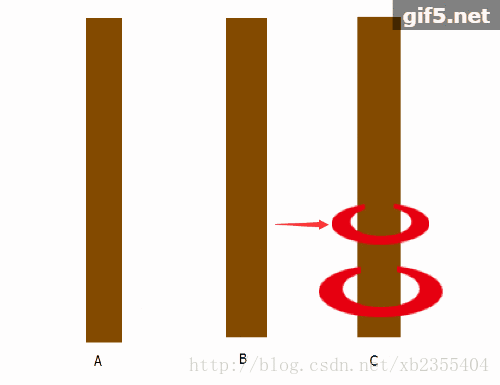
以上是来自https://blog.csdn.net/qq_41282102/article/details/85061198的图片。
从以上n=2时的动图中可以发现,B相当于作为放置的媒介,而最关键的问题是:交换A与C的位置,那么B处就可以直接将小圆盘再放置上就大功告成!
于我而言,递归递归关键的点在于要去找到这问题其中的共性或者说是规律。。。。参考https://blog.csdn.net/qq_41282102/article/details/85061198
结论:
其实2阶汉诺塔相当于执行了三大步骤:
1.在ACB的顺序下执行了一阶汉诺塔的移法
2.从A->C移动了最大盘
3.在BAC的顺序下执行了一阶汉诺塔的移法
同理,推广到三阶的时候,我们将小环和中环视为一个整体,我们是否又变成了执行二阶汉诺塔方法了呢?
那么四阶前三个环视为整体,五阶前四个环视为整体等等。。。所以我们已经找到了解决汉诺塔方法的递归算法。
代码:
def hano(n,a,b,c):
if n == 1:
print(a,'-->',c)
else:
hano(n-1,a,c,b)
hano(1,a,b,c)
hano(n-1,b,a,c)
hano(3,'A','B','C')
n=3(移动三个盘子)时运行结果:
A --> C
A --> B
C --> B
A --> C
B --> A
B --> C
A --> C
版权归原作者 多思考多睡觉 所有, 如有侵权,请联系我们删除。