系列文章目录
- 初识推荐系统——基于Spark平台的协同过滤实时电影推荐系统项目系列博客(一)
- 利用用户行为数据——基于Spark平台的协同过滤实时电影推荐系统项目系列博客(二)
- 项目主要效果展示——基于Spark平台的协同过滤实时电影推荐系统项目系列博客(三)
- ……
项目资源下载
- 电影推荐系统网站项目源码Github地址(可Fork可Clone)
- 电影推荐系统网站项目源码Gitee地址(可Fork可Clone)
- 电影推荐系统网站项目源码压缩包下载(直接使用)
- 电影推荐系统网站项目源码所需全部工具合集打包下载(spark、kafka、flume、tomcat、azkaban、elasticsearch、zookeeper)
- 电影推荐系统网站项目源数据(可直接使用)
- 电影推荐系统网站项目个人原创论文
- 电影推荐系统网站项目前端代码
- 电影推荐系统网站项目前端css代码
文章目录
前言
今天将为大家带来系列博客的第二篇博文,也就是关于如何利用用户行为数据,以便于我们得到更好的推荐结果。今天的内容有些难度,并且文章内容比较多,希望大家沉下心来,因为这里的理论知识直接关系到后面的实践操作,我会一个字一个字的把这篇博文完成,估计一次写不完,所以时间可能需要长一些,我会尽自己最大的可能让内容看起来通俗易懂,下面就开始今天的学习吧!
一、用户行为数据简介
既然要做个性化推荐系统,首先我们需要先了解每个人,听其言、观其行,在网络世界我们称之为用户行为数据
有些用户不是太清楚自己喜欢什么
用户的兴趣不可能是一成不变的,会根据外部因素进行改变
我们需要通过不断采集用户在网络中的行为数据以及用户与网站的交互反馈数据,不断修正推荐系统对用户的定位,从而不断修正符合用户当前状态的的推荐结果
协同过滤是目前比较热门的推荐系统算法,协同:用户与用户之间、用户和网站之间等进行不断地互动,慢慢过滤掉自己不感兴趣的物品,从而满足自己的需求
用户行为数据在网站上最简单的存在形式就是日志。网站在运行过程中会产生大量的原始日志R A W L O G RAW LOGRAWLOG,将其存储在文件系统中,企业会将多种原始日志按照用户行为汇总成会话日志
S E S S I O N L O G SESSION LOGSESSIONLOG,每一个会话日志表示用户的一种反馈。
用户反馈主要分为显性反馈行为和隐形反馈行为。显性反馈行为包括用户明确表示对物品喜好的行为。比如评分系统;隐形反馈行为是指那些不能够明确反应用户喜好的行为。比如用户浏览页面的行为日志,我们对表示用户喜欢的反馈叫正反馈,表示不喜欢的叫负反馈,下表为显性反馈数据和隐形反馈数据的比较:
显性反馈数据隐形反馈数据用户兴趣明确不明确数量较少庞大存储数据库分布式文件系统实时读取实时有延迟正负反馈都有只有正反馈
下表为各代表网站中显性反馈数据和隐形反馈的例子:
显性反馈隐形反馈视频网站用户对视频的评分用户观看视频的日志、浏览视频页面的日志电子商务网站用户对商品的评分购买日志、浏览日志门户网站用户对新闻的评分浏览新闻的日志音乐网站用户对音乐/歌手/专辑的评分听歌的日志
那么用户的行为表示成什么呢?一些比较中立的字段(用户行为的统一表示)如下:
表示用户行为①user id产生行为的用户的唯一标识②item id产生行为的对象的唯一标识③behavior type行为的种类(比如是购买还是浏览)④context产生行为的上下文,包括时间和地点等⑤behavior weight行为的权重(如果是观看视频的行为,那么这个权重可以是观看时长;如果是打分行为,这个权重可以是分数)⑥behavior content行为的内容(如果是评论行为,那么就是评论的文本,如果是打标签的行为,就是标签)
当然,可以根据自己的实际情况去设计日志的表示形式
有代表性的数据集会是如下4种:
- 无上下文信息的隐性反馈数据集,每一条行为记录仅仅包含用户ID和物品ID
- 无上下文信息的显性反馈数据集,每一条记录包含用户ID、物品ID和用户对物品的评分
- 有上下文信息的隐性反馈数据集,每一条记录包含用户ID、物品ID和用户对物品产生行为的时间戳
- 有上下文信息的显性反馈数据集,每一条记录包含用户ID、物品ID和用户对物品的评分和评分发生的时间戳
二、用户行为分析
2.1 用户活跃度和物品流行度的分布
二八定律:19世纪末20世纪初意大利经济学家帕累托发明“二八定律”,认为在任何一组东西中,最重要的只占其中一小部分,约
20
%
20\%
20%,其余
80
%
80\%
80%的尽管是多数,却是次要的。很多商家企业认为
80
%
80\%
80%的公司利润来自
20
%
20\%
20%的重要客户,其余
20
%
20\%
20%的利润则来自
80
%
80\%
80%的普通客户,传统零售情愿把
80
%
80\%
80%的资源花在能创造出关键利润的
20
%
20\%
20%方面,从把
20
%
20\%
20%的资源花费在
80
%
80\%
80%的普通客户群里
长尾理论:流行的,被人熟知的东西都是所谓的“头”,而常常被人忽视的,不流行的,个性化就是所谓的“尾”,而在营销界对“尾巴”的挖掘,可以创造出惊人的利润和价值,“小利润大市场”。“虽然赚很少的钱,但是我们要赚很多人的钱”,这就是长尾理论在营销界的真正含义。用户活跃度和物品流行度都符合长尾理论,下图为物品流行度的长尾分布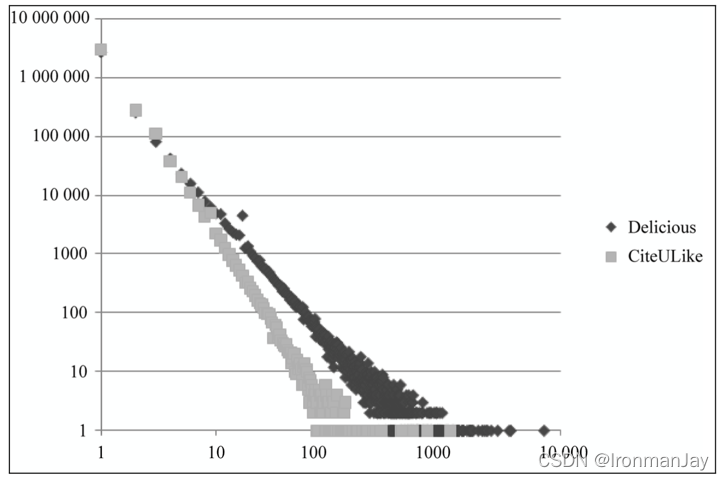
上图展示了Delicious和CiteULike数据集中物品流行度的分布曲线。横坐标是物品的流行度
K
K
K,纵坐标是流行度为
K
K
K的物品的总数。这里,物品的流行度指物品产生过行为的用户总数。但是,这个又揭示了什么?
流行的物品总是少数,不流行的占绝大多数,如果能让不流行的物品流行起来,那么会创造很大利润,下图为用户活跃度的长尾分布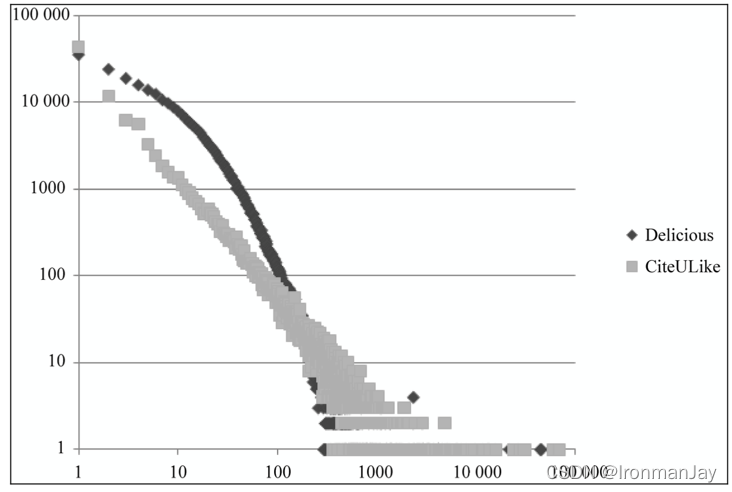
上图展示了Delicious和CiteULike数据集中用户活跃度的分布曲线。横坐标是用户的活跃度
K
K
K,纵坐标是活跃度为
K
K
K的用户总数。这里,用户的活跃度为用户产生过行为的物品总数。但是,这个又揭示了什么?
非常活跃的用户总是少数,大多数用户都是不活跃的,如果能把不活跃的用户都调用起来,那么会创造很大的利润。那么推荐引擎又是做什么的呢?通过个性化的推荐,将不流行的物品推送给不活跃的人,激活这两部分,要比将流行的物品推送给活跃的人的市场大很多,这就是互联网思维
2.2 用户活跃度和物品流行度的关系
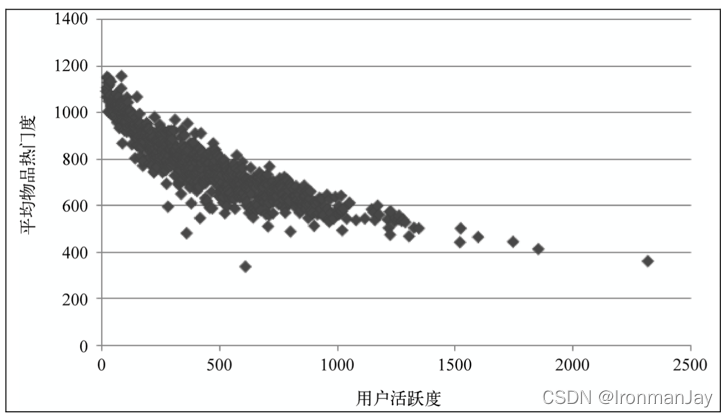
一般来说,不活跃的用户要么是新用户,要么是只来过网站一两次的老用户。那么,不同活跃度的用户喜欢的物品的流行度是否有差别?一般认为,新用户倾向于浏览热门的物品,因为他们对网站还不熟悉,只能点击首页的热门物品,而老用户会逐渐开始浏览冷门的物品。下图展示了
M
o
v
i
e
L
e
n
s
MovieLens
MovieLens数据集中用户活跃度和物品流行度之间的关系,其中横坐标是用户活跃度,纵坐标是具有某个活跃度的所有用户评过分的物品的平均流行度。如图所示,图中曲线呈明显下降的趋势,这表明用户越活跃,越倾向于浏览冷门的物品。
基于用户行为数据设计的推荐算法一般称为协同过滤算法。学术界对于实现协同过滤有很多方法,比如基于领域的方法(
n
e
i
g
h
b
o
r
h
o
o
d
−
b
a
s
e
d
neighborhood-based
neighborhood−based)、隐语义模型(
l
a
t
e
n
t
f
a
c
t
o
r
m
o
d
e
l
latent factor model
latentfactormodel)、基于图的随机游走算法(
r
a
n
d
o
m
w
a
l
k
o
n
g
r
a
p
h
random walk on graph
randomwalkongraph)等。目前使用最广泛的是基于领域的方法,主要包括下面两个算法:
- 基于用户的协同过滤算法,这种算法给用户推荐和他兴趣相似的其他用户喜欢的物品
- 基于物品的协同过滤算法,这种算法给用户推荐和他之前喜欢的物品相似的物品
三、精确率和召回率
考虑一个二分问题,即将实例分成正类(
p
o
s
i
t
i
v
e
positive
positive)或负类(
n
e
g
a
t
i
v
e
negative
negative)。对于一个二分问题来说,会出现四种情况。如果一个实例是正类并且也被预测成正类,即为真正类(
T
r
u
e
p
o
s
i
t
i
v
e
True \quad positive
Truepositive),如果实例是负类被预测成正类,称之为假正类(
F
a
l
s
e
p
o
s
i
t
i
v
e
False \quad positive
Falsepositive)。相应的,如果实例是负类被预测成负类,称之为真负类(
T
r
u
e
n
e
g
a
t
i
v
e
True \quad negative
Truenegative),正类被预测成负类则为假负类(
F
a
l
s
e
n
e
g
a
t
i
v
e
False \quad negative
Falsenegative)
T P TP TP:正确肯定的数目F N FN FN:漏报、没有正确找到匹配的数目F P FP FP:误报、给出的匹配是不正确的
列联表如下表所示,1代表正类,0代表负类:T N TN TN:正确拒绝的非匹配对数
预测1预测0实际1True Positive(TP)False Negative(FN)实际0False Positive(FP)True Negative(TN)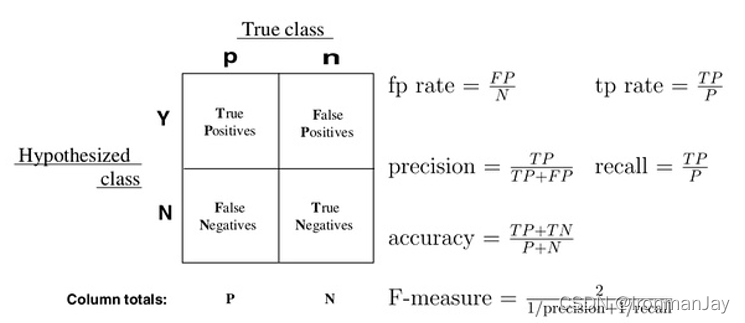
精确率(正确率)和召回率是广泛用于信息检索和统计学分类领域的两个度量值,用来评价结果的质量。其中精度是检索出相关文档数与检索出的文档总数的比率,衡量的是检索系统的查准率;召回率是指检索出的相关文档数和文档库中所有的相关文档数的比率,衡量的是检索系统的查全率
一般来说,
P
r
e
c
i
s
i
o
n
Precision
Precision就是检索出来的条目(比如:文档、网页等)有多少是准确的,
R
e
c
a
l
l
Recall
Recall就是所有准确的条目有多少被检索出来了,两者的定义分别如下:
P r e c i s i o n Precision Precision = 提取出的正确信息条数 / 提取出的信息条数R e c a l l Recall Recall = 提取出的正确信息条数 / 样本中的信息条数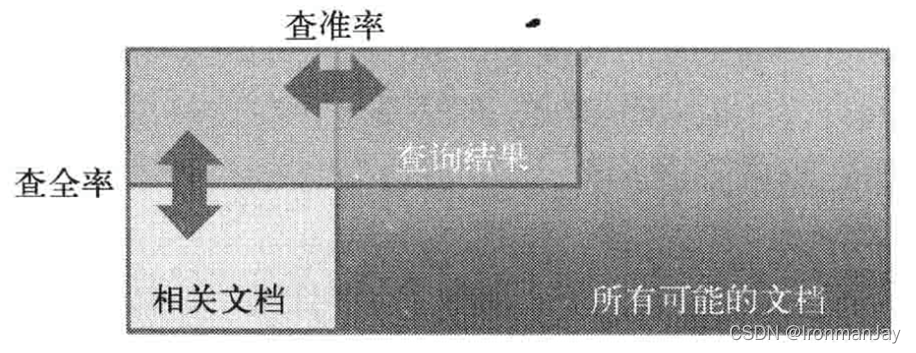为了能够评价不同算法的优劣,在
P r e c i s i o n PrecisionPrecision和
R e c a l l RecallRecall的基础上提出了
F 1 F1F1值得概念,来对
P r e c i s i o n PrecisionPrecision和
R e c a l l RecallRecall进行整体评价。
F 1 F1F1的定义如下:
F 1 F1 F1值 = 正确率 * 召回率 * 2 / (正确率 + 召回率)不妨举这样一个例子:某池塘有1400条鲤鱼,300只虾,300只鳖。现在以捕鲤鱼为目的。撒一大网,逮着700条鲤鱼,200只虾,100只鳖。那么,这些指标分别如下:
正确率 = 700 / (700 + 200 + 100) = 70%
召回率 = 700 / 1400 = 50%
F 1 F1 F1值 = 70% * 50% * 2 / (70% + 50%) = 58.3%不妨看看如果把池子里所有的鲤鱼、虾和鳖都一网打尽,这些指标又有何变化:
正确率 = 1400 / (1400 + 300 + 300) = 70%
召回率 = 1400 / 1400 = 100%
F 1 F1 F1值 = 70% * 100% * 2 / (70% + 100%) = 82.35%由此可见,正确率是评估捕获的成果中目标成果所占的比例;召回率,顾名思义,就是从关注领域中,召回目标类别的比例;而
F FF值,则是综合这二者指标的评估指标,用于综合反应整体的指标
当然希望检索结果P r e c i s i o n PrecisionPrecision越高越好,同时
R e c a l l RecallRecall也越高越好,但事实上这两者在某些情况下有矛盾的。比如在极端情况下,我们只搜索出了一个结果,且是准确的,那么
P r e c i s i o n PrecisionPrecision就是
100 % 100\%100%,但是
R e c a l l RecallRecall就很低;而如果我们把所有结果都返回,那么比如
R e c a l l RecallRecall是
100 % 100\%100%,但是
P r e c i s i o n PrecisionPrecision就会很低。因此在不同的场合需要自己判断希望
P r e c i s i o n PrecisionPrecision比较高还是
R e c a l l RecallRecall比较高。如果是做实验研究,可以绘制
P r e c i s i o n − R e c a l l Precision-RecallPrecision−Recall曲线来帮助分析
四、基于内容的推荐算法
基于内容的推荐算法,原理是用户喜欢和自己关注过的
I
t
e
m
Item
Item在内容上类似的
I
t
e
m
Item
Item,如比你看了哈利波特
Ⅰ
Ⅰ
Ⅰ,基于内容的推荐算法发现哈利波特
Ⅱ
−
Ⅶ
Ⅱ-Ⅶ
Ⅱ−Ⅶ,与你以前观看的在内容上面(共有很多关键词)有很大的关联性,就把后者推荐给你,本项目中采用
E
l
a
s
t
i
c
S
e
a
r
c
h
ElasticSearch
ElasticSearch来实现多个电影之间的相似度计算
五、基于模型的推荐算法
该类型的推荐算法是通过预先设定的计算模型来实现推荐,常常用于实时推荐,相比其他离线推荐算法可以缩短推荐实现,本项目中实时推荐算法通过根据具体业务构建了相应的推荐模型来实现推荐
六、协同过滤推荐算法
6.1 协同过滤算法思想
比如你想看一个电影,但是不知道具体看哪一部,你会怎么做?有两种方法,一种是问问周围兴趣相同的朋友,看看他们最近有什么好的电影推荐。另外一种是看看电影的相似程度,比如都喜欢看科幻片,那就会找电影名带有科幻、科技之类的电影
协同过滤算法就是基于上面的思想,主要包含基于用户的协同过滤推荐算法以及基于物品的协同过滤推荐算法
实现协同过滤,一般需要几个步骤:
- 收集用户偏好
- 找到相似的用户或者物品
- 计算推荐
6.2 推荐数据准备
要进行推荐我们需要的数据如下:用户ID、物品ID、偏好值
偏好值就是用户对物品的喜爱程度,推荐系统所能做的事就是根据这些数据为用户推荐他还没有见过的物品,并且猜测这个物品用户喜欢的概论比较大
用户ID和物品ID一般通过系统的业务数据库就可以获得,偏好值的采集一般会有很多方法,比如评分、投票、转发、保存书签、页面停留时间等等,然后系统根据用户的这些行为流水,采取减噪、归一化、加权等方法综合给出偏好值。一般不同的业务系统给出偏好值的计算方法不一样
6.3 相似性度量
基于用户的推荐和基于物品的推荐都需要找相似,即需要找相似用户以及相似物品。比如一个男生和一个女生是朋友,不能将该女生穿的衣服推荐给男生。要找相似。那么衡量的指标有那些?比如皮尔逊相关系数、欧氏距离、同现相似度、
C
o
s
i
n
e
Cosine
Cosine相似度、
T
a
n
i
m
o
t
o
Tanimoto
Tanimoto系数等
6.3.1 皮尔逊相关系数
皮尔逊相关系数是介于1到-1之间的数,它衡量两个一一对应的序列之间的线性相关性。也就是两个序列一起增大或者一起减小的可能性。两个序列正相关值就趋近于1,否则趋近于0。数学含义:两个序列协方差与二者方差乘积的比值
r
=
∑
i
=
1
n
(
X
i
−
X
‾
)
(
Y
i
−
Y
‾
)
∑
i
=
1
n
(
X
i
−
X
‾
)
2
∑
i
=
1
n
(
Y
i
−
Y
‾
)
2
r=\frac{\sum_{i=1}^{n}(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{\sum_{i=1}^{n}(X_i-\overline{X})^2}\sqrt{\sum_{i=1}^{n}(Y_i-\overline{Y})^2}}
r=∑i=1n(Xi−X)2∑i=1n(Yi−Y)2∑i=1n(Xi−X)(Yi−Y)
如果比较两个人的相似度,那么他们所有共同评价过的物品可以看做两个人的特征序列,这两个特征序列的相似度就可以用皮尔逊相关系数去衡量。物品的相似度比较也是如此。皮尔逊对于稀疏矩阵表现不好,可以通过引入权重进行优化
6.3.2 欧氏距离
欧式距离同理可以将两个人所有共同评价过的物品看做这个人的特征,将这些特征看作是空间中的点,计算两点之间的距离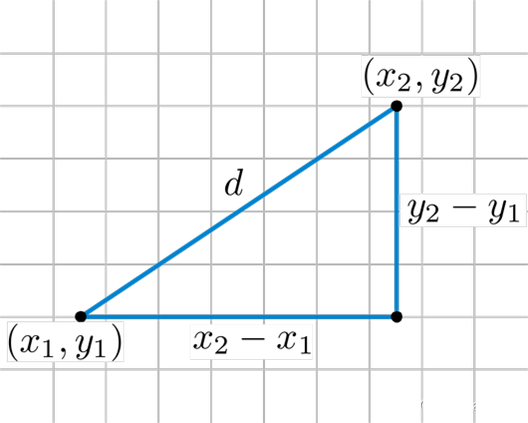
6.3.3 同现相似度
物品
i
i
i和物品
j
j
j的同现相似度公式定义如下:
w
i
j
=
∣
N
(
i
)
⋂
N
(
j
)
∣
∣
N
(
i
)
∣
w_{ij} = \frac{| N(i)\bigcap N(j)|}{|N(i)|}
wij=∣N(i)∣∣N(i)⋂N(j)∣
其中,分母是喜欢物品
i
i
i的用户数,而分子则是同时喜欢物品
i
i
i和物品
j
j
j的用户数。因此,上述公式可用理解为喜欢物品
i
i
i的用户有多少比例的用户也喜欢
j
j
j(和关联规则类似)。
但上述公式存在一个问题,如果物品
j
j
j是热门物品,有很多人都喜欢,则会导致
w
i
j
w_{ij}
wij很大,接近于1。因此会造成任何物品都和热门物品有很大的相似度。为此我们用如下公式进行修正:
w
i
j
=
∣
N
(
i
)
⋂
N
(
j
)
∣
∣
N
(
i
)
∣
∣
N
(
j
)
∣
w_{ij} = \frac{| N(i)\bigcap N(j)|}{\sqrt{|N(i)||N(j)|}}
wij=∣N(i)∣∣N(j)∣∣N(i)⋂N(j)∣
这个公式惩罚了 物品
j
j
j的权重,因此减轻了热门物品和很多物品相似的可能性。(也归一化了
[
i
,
j
]
[i,j]
[i,j]和
[
j
,
i
]
[j,i]
[j,i])
6.4 领域大小
有了相似度的比较,那么比较多少个用户或者物品为好呢?一般会有基于固定大小的邻域及基于阈值的邻域。具体数值一般是通过对模型的评比分数进行调整优化
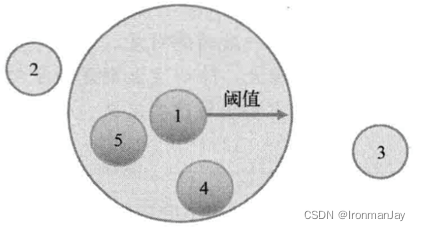
6.5 基于用户的
C
F
CF
CF
U
s
e
r
C
F
(
U
s
e
r
C
o
l
l
a
b
o
r
a
t
i
o
n
F
i
l
t
e
r
)
UserCF(User \quad Collaboration \quad Filter)
UserCF(UserCollaborationFilter),又称之为基于用户的协同过滤算法。模型核心算法伪代码表示如下:
for 每个其他用户w
计算用户u和用户w的相似度s
按相似度排序后,将位置靠前的用户作为邻域n
for(n中用户有偏好,而u中用户无偏好的)每个物品i
for(n中用户对i有偏好的)每个其他用户v
计算用户u和用户v的相似度s
按权重s将v对i的偏好并入平均值
基于该核心算法,完成用户商品矩阵如下所示:
物品101物品102物品103用户13.02.01.0用户21.02.03.0用户31.0--用户42.0-1.0用户53.02.01.0
预测用户对未评分的物品的分值,然后按照降序排序,进行推荐
6.6 基于物品的
C
F
CF
CF
I
t
e
m
C
F
(
I
t
e
m
C
o
l
l
a
b
o
r
a
t
i
o
n
F
i
l
t
e
r
)
ItemCF(Item \quad Collaboration \quad Filter)
ItemCF(ItemCollaborationFilter),又称之为基于商品(物品)的协同过滤算法。先计算出物品-物品的相似矩阵,伪代码如下所示:
for 每个物品i
for 每个其他物品j
for 对i和j均有偏好的每个用户u
将物品对(i与j)间的偏好值差异加入u的偏好
基于上面的结果:
for 用户u未表达过偏好的每个物品i
for 用户u表达过偏好的每个物品j
找到j与i之间的平均偏好值差异
添加该差异到u对j的偏好值
添加其至平均值
return 值最高的物品(按平均差异排序)
给用户推送预测偏好值
n
n
n个最高的物品
6.7
A
L
S
ALS
ALS矩阵分解模型
6.7.1 矩阵分解模型
在协同过滤推荐算法中,最主要是的产生用户对物品的打分,用户对物品的打分行为可以表示成一个评分矩阵
A
(
m
∗
n
)
A(m*n)
A(m∗n),表示
m
m
m个用户对
n
n
n个物品的打分情况。如下图所示:
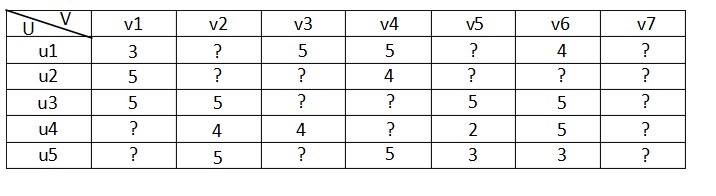
其中
A
(
i
,
j
)
A(i,j)
A(i,j)表示用户
u
s
e
r
i
user i
useri对物品
i
t
e
m
j
item j
itemj的打分。但是,用户不会对所有物品打分,图中
?
?
?表示用户没有打分的情况,所以这个矩阵
A
A
A很多元素都是空的,我们称其为“损失值(missing value)”,是一个稀疏矩阵。在推荐系统中,我们希望得到用户对所有物品的打分情况,如果用户没有对一个用户打分,那么就需要预测用户是否会对该物品打分,以及会打多少分。这就是所谓的“矩阵补全(填空)”
我们从另外一个层面考虑用户对物品的喜爱程度,而不是通过与用户的推荐。用户之所以喜欢一个物品,绝大多数是因为这个物品的某些属性和这个用户的属性是一致的或者是接近的,比如一个人总是具有爱国情况或者侠义情怀,那么根据这些推断一定喜欢比如《射雕英雄传》、抗战剧等电视剧,因为这些电视剧所表达的正是侠义和爱国。可以设想用户拥有某些隐含的特征、物品也具有某种隐含的特征,如果这些特征都相似,那么很大程度上用户会喜欢这个物品
根据上面的假设,我们可以把评分矩阵表示成两个低纬度的矩阵相乘,如下:
我们希望学习一个
P
P
P代表
u
s
e
r
user
user的特征,
Q
Q
Q代表
i
t
e
m
item
item的特征。特征的每一个维度代表一个隐性因子,比如对电影来说,这些隐性因子可能是导演、演员等。当然,这些隐性因子是机器学习到的,具体是什么含义我们不确定
A
L
S
ALS
ALS的核心就是下面这个假设:打分矩阵
A
A
A是近似低秩的。换句话说,一个
m
∗
n
m*n
m∗n的打分矩阵
A
A
A可以用两个小矩阵
U
(
m
∗
k
)
U(m*k)
U(m∗k)和
V
(
n
∗
k
)
V(n*k)
V(n∗k)的乘积来近似:
A
≈
U
V
T
,
K
≪
m
,
n
A≈UV^T,K \ll m,n
A≈UVT,K≪m,n。这样我们就把整个系统的时间复杂度由
O
(
m
n
)
O(mn)
O(mn)一下降到了
O
(
(
m
+
n
)
∗
k
)
O((m+n)*k)
O((m+n)∗k)。一个人的喜好程度映射到了一个低维向量
u
i
u_i
ui,一个电影的特征就变成了维度相同的向量
v
j
v_j
vj,那么这个人和这个电影的相似度就可以表述成这两个向量之间的内积
u
i
T
v
j
{u_i}^Tv_j
uiTvj
我们可以把打分理解成相似度,那么“打分矩阵
A
(
m
∗
n
)
A(m*n)
A(m∗n)”就可以由"用户喜好特征矩阵
U
(
m
∗
k
)
U(m*k)
U(m∗k)"和“产品特征矩阵
V
(
n
∗
k
)
V(n*k)
V(n∗k)”的乘积
U
V
T
UV^T
UVT来近似了。这种方法被称为概率矩阵分解算法(
p
r
o
b
a
b
i
l
i
s
t
i
c
m
a
t
r
i
x
f
a
c
t
o
r
i
z
a
t
i
o
n
,
P
M
F
probabilistic matrix factorization,PMF
probabilisticmatrixfactorization,PMF)。
A
L
S
ALS
ALS算法是
P
M
F
PMF
PMF在数值计算方面的应用。
6.7.2 交替最小二乘法(
A
L
S
ALS
ALS)
为了使低秩矩阵
X
X
X和
Y
Y
Y尽可能地逼近
R
R
R,需要最小化下面地平方误差损失函数
m
i
n
x
∗
,
y
∗
∑
u
,
i
i
s
k
n
o
w
n
(
r
u
i
−
x
u
T
y
i
)
2
min_{x_*,y_*}\sum_{u,i \quad is \quad known}^{}(r_{ui}-{x_u}^Ty_i)^2
minx∗,y∗u,iisknown∑(rui−xuTyi)2
考虑到矩阵的稳定性问题,使用吉洪诺夫正则化
T
i
k
h
o
n
o
v
r
e
g
u
l
a
r
i
z
a
t
i
o
n
Tikhonov regularization
Tikhonovregularization,则上式变为:
m
i
n
x
∗
,
y
∗
L
(
X
,
Y
)
=
m
i
n
x
∗
,
y
∗
∑
u
,
i
i
s
k
n
o
w
n
(
r
u
i
−
x
u
T
y
i
)
2
+
λ
(
∣
x
u
∣
2
+
∣
y
i
∣
2
)
min_{x_*,y_*} L(X,Y) = min_{x_*,y_*} \sum_{u,i \quad is \quad known}^{}(r_{ui}-{x_u}^Ty_i)^2+\lambda (|x_u|^2+|y_i|^2)
minx∗,y∗L(X,Y)=minx∗,y∗u,iisknown∑(rui−xuTyi)2+λ(∣xu∣2+∣yi∣2)
所以整个矩阵分解模型的损失函数为:
C
=
∑
(
i
,
j
)
∈
R
[
(
a
i
,
j
−
u
i
T
v
j
)
2
+
λ
(
∣
∣
u
i
∣
∣
2
+
∣
∣
v
j
∣
∣
2
)
]
C=\sum_{(i,j) \in R}^{}[(a_{i,j}-{u_i}^Tv_j)^2+\lambda (||u_i||^2+||v_j||^2)]
C=(i,j)∈R∑[(ai,j−uiTvj)2+λ(∣∣ui∣∣2+∣∣vj∣∣2)]
有了损失函数之后,下面就开始谈优化方法了,通常的优化方法分为两种:交叉最小二乘法(
a
l
t
e
r
n
a
t
i
v
e
l
e
a
s
t
s
q
u
a
r
e
s
alternative \quad least \quad squares
alternativeleastsquares)和随机梯度下降法(
s
t
o
c
h
a
s
t
i
c
g
r
a
d
i
e
n
t
d
e
s
c
e
n
t
stochastic \quad gradient \quad descent
stochasticgradientdescent)。本次使用交叉最小二乘法(
A
L
S
ALS
ALS)来最优化损失函数。算法的思想就是:我们先随机生成
U
(
0
)
U^{(0)}
U(0),然后固定它求解
V
(
0
)
V^{(0)}
V(0),再固定
V
(
0
)
V^{(0)}
V(0)求解
U
(
1
)
U^{(1)}
U(1),这样交替进行下去,直到取得最优解
m
i
n
(
C
)
min(C)
min(C)。因为每步迭代都会降低误差,并且误差是有下界的,所以
A
L
S
ALS
ALS一定会收敛。但由于问题是非凸的,
A
L
S
ALS
ALS并不保证会收敛到全局最优解。但在实际应用中,
A
L
S
ALS
ALS对初始点不是很敏感,是不是全局最优解造成的影响并不大
算法的执行步骤如下:
先随机生成一个 U ( 0 ) U^{(0)} U(0)。一般可以取0值或者全局均值
固定 U ( 0 ) U^{(0)} U(0)(即:认为 U ( 0 ) U^{(0)} U(0)是已知的常量),来求解 V ( 0 ) V^{(0)} V(0)
此时,损失函数为: C = ∑ ( i , j ) ∈ R [ ( a i , j − ( u i ( 0 ) ) T v j ) 2 + λ ( ∣ ∣ u i ( 0 ) ∣ ∣ 2 + ∣ ∣ v j ∣ ∣ 2 ) ] C=\sum_{(i,j) \in R}^{}[(a_{i,j}-({u_i}^{(0)})^Tv_j)^2+\lambda (||{u_i}^{(0)}||^2+||v_j||^2)]C=(i,j)∈R∑[(ai,j−(ui(0))Tvj)2+λ(∣∣ui(0)∣∣2+∣∣vj∣∣2)]
由于
C
C
C中只有V j V_jVj一个未知变量,因此
C CC的最优化问题转换为最小二乘问题,用最小二乘法求解
V j V_jVj的最优解。固定
j ( j = 1 , 2 , … … , n ) j(j=1,2,……,n)j(j=1,2,……,n),则
C CC的导数
∂ C ∂ v j = ∂ ∂ v j [ ∑ i = 1 m [ ( a i , j − ( u i ( 0 ) ) T ) v j ) 2 + λ ( ∣ ∣ u i ( 0 ) ∣ ∣ 2 + ∣ ∣ v j ∣ ∣ 2 ) ] ] = ∑ i = 1 m [ 2 ( a i , j − ( u i ( 0 ) ) T ) v j ) ( − u i ( 0 ) ) + 2 λ v j ] = 2 ∑ i = 1 m [ ( ( u i ( 0 ) ) T u i ( 0 ) + λ ) v j − a i , j u i ( 0 ) ] \frac{\partial C}{\partial v_j}=\frac{\partial }{\partial v_j}[\sum_{i=1}^{m}[(a_{i,j}-({u_i}^{(0)})^T)v_j)^2+\lambda (||{u_i}^{(0)}||^2+||v_j||^2)]]=\sum_{i=1}^{m}[2(a_{i,j}-({u_i}^{(0)})^T)v_j)(-{u_i}^{(0)})+2\lambda v_j]=2\sum_{i=1}^{m}[(({u_i}^{(0)})^T{u_i}^{(0)}+\lambda )v_j-a_{i,j}{u_i}^{(0)}]∂vj∂C=∂vj∂[i=1∑m[(ai,j−(ui(0))T)vj)2+λ(∣∣ui(0)∣∣2+∣∣vj∣∣2)]]=i=1∑m[2(ai,j−(ui(0))T)vj)(−ui(0))+2λvj]=2i=1∑m[((ui(0))Tui(0)+λ)vj−ai,jui(0)]
令
∂
C
∂
v
j
=
0
\frac{\partial C}{\partial v_j}=0
∂vj∂C=0,得到:∑ i = 1 m [ ( ( u i ( 0 ) ) T u i ( 0 ) + λ ) v j ] = ∑ i = 1 m a i , j u i ( 0 ) \sum_{i=1}^{m}[(({u_i}^{(0)})^T{u_i}^{(0)}+\lambda )v_j]=\sum_{i=1}^{m}a_{i,j}{u_i}^{(0)}i=1∑m[((ui(0))Tui(0)+λ)vj]=i=1∑mai,jui(0)
即:
(
U
U
T
+
λ
E
)
v
j
=
U
a
j
T
(UU^T+\lambda E)v_j=U{a_j}^T
(UUT+λE)vj=UajT
令:
M
1
=
U
U
T
+
λ
E
,
M
2
=
U
a
j
T
M_1 = UU^T+\lambda E,M_2 = U{a_j}^T
M1=UUT+λE,M2=UajT
则:
v
j
=
M
1
−
1
M
2
v_j = {M_1}^{-1}M_2
vj=M1−1M2
按照上式依次计算
v
1
,
v
2
,
…
…
,
v
n
v_1,v_2,……,v_n
v1,v2,……,vn,从而得到V ( 0 ) V^{(0)}V(0)
固定 V ( 0 ) V^{(0)} V(0)(即:认为 V ( 0 ) V^{(0)} V(0)是已知的量),来求解 U ( 1 ) U^{(1)} U(1)。此时,损失函数为:
C = ∑ ( i , j ) ∈ R [ ( a i , j − ( u i ) T v j ( 0 ) ) 2 + λ ( ∣ ∣ u i ∣ ∣ 2 + ∣ ∣ v j ( 0 ) ∣ ∣ 2 ) ] C=\sum_{(i,j) \in R}^{}[(a_{i,j}-({u_i})^T{v_j}^{(0)})^2+\lambda (||{u_i}||^2+||{v_j}^{(0)}||^2)]C=(i,j)∈R∑[(ai,j−(ui)Tvj(0))2+λ(∣∣ui∣∣2+∣∣vj(0)∣∣2)]
同理,用步骤2类似的方法,可以计算
u
i
u_i
ui的值:∂ C ∂ u i = 2 ∑ j = 1 n [ ( ( v j ( 0 ) ) T v j ( 0 ) + λ ) u i − a i , j v j ( 0 ) ] \frac{\partial C}{\partial u_i}=2\sum_{j=1}^{n}[(({v_j}^{(0)})^T{v_j}^{(0)}+\lambda )u_i-a_{i,j}{v_j}^{(0)}]∂ui∂C=2j=1∑n[((vj(0))Tvj(0)+λ)ui−ai,jvj(0)]
令
∂
C
∂
u
i
=
0
\frac{\partial C}{\partial u_i}=0
∂ui∂C=0,得到:∑ j = 1 n [ ( ( v j ( 0 ) ) T v j ( 0 ) + λ ) u i ] = ∑ j = 1 n a i , j v j ( 0 ) \sum_{j=1}^{n}[(({v_j}^{(0)})^T{v_j}^{(0)}+\lambda )u_i]=\sum_{j=1}^{n}a_{i,j}{v_j}^{(0)}j=1∑n[((vj(0))Tvj(0)+λ)ui]=j=1∑nai,jvj(0)
即:
(
V
V
T
+
λ
E
)
u
i
=
V
a
i
T
(VV^T+\lambda E)u_i=V{a_i}^T
(VVT+λE)ui=VaiT
令:
M
1
=
V
V
T
+
λ
E
,
M
2
=
V
a
i
T
M_1 = VV^T+\lambda E,M_2 = V{a_i}^T
M1=VVT+λE,M2=VaiT
则:
u
i
=
M
1
−
1
M
2
u_i = {M_1}^{-1}M_2
ui=M1−1M2
依照上式依次计算
u
1
,
u
2
,
…
…
,
u
m
u_1,u_2,……,u_m
u1,u2,……,um,从而得到U ( 1 ) U^{(1)}U(1)
4.循环执行步骤2、3,直到损失函数
C CC的值收敛(或者设置一个迭代次数
N NN,迭代执行步骤2、3
N NN次后)。这样,就得到了
C CC最优解对应的矩阵
U UU、
V VV
七、组合推荐
推荐算法有很多种,本项目只涉及到了基于内容的推荐、基于模型的实时推荐以及协同过滤推荐。这种组合式的应用推荐就叫组合推荐(
H
y
b
r
i
d
R
e
c
o
m
m
e
n
d
a
t
i
o
n
Hybrid \quad Recommendation
HybridRecommendation)。研究和应用最多的是内容推荐和协同过滤推荐的组合。最简单的做法就是分别用基于内容的方法和协同过滤推荐方法去产生一个推荐预测结果,然后用某种方法组合其结果
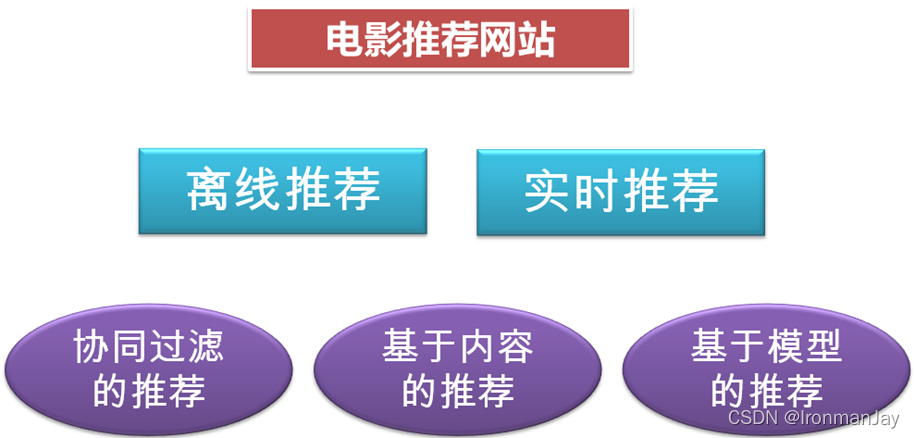
八、我们要做什么
总结
哇,终于写完了,历时差不多四天,这篇博文又长又有难度,希望读者好好理解,里面有一些高等数学相关的知识,但是内容不是特别难,这里的理论对于后面的实践操作至关重要,我已经说过很多次了。后面的博客就是正式开始搭建我们整个系统了,下一篇先给大家带来关于系统展示的相关内容!
版权归原作者 IronmanJay 所有, 如有侵权,请联系我们删除。