0
0

Rust每日一练(Leetday0016) 全排列I\II、旋转图像

46. 全排列 Permutations

给定一个不含重复数字的数组 

nums

，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

**输入：**nums = [1,2,3]
**输出：**[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

**输入：**nums = [0,1]
**输出：**[[0,1],[1,0]]

示例 3：

**输入：**nums = [1]
**输出：**[[1]]

提示：

  • 1 <= nums.length <= 6
  • -10 <= nums[i] <= 10
  • nums 中的所有整数 互不相同

**代码： **回溯法

fn permute(nums: Vec<i32>) -> Vec<Vec<i32>> {
    let mut res: Vec<Vec<i32>> = Vec::new();
    if nums.len() == 0 {
        return res;
    }
    let mut used: Vec<bool> = vec![false; nums.len()];
    fn backtrack(path: &mut Vec<i32>, res: &mut Vec<Vec<i32>>, nums: &Vec<i32>, used: &mut Vec<bool>) {
        if path.len() == nums.len() {
            let tmp = path.clone();
            res.push(tmp);
            return;
        }
        for i in 0..nums.len() {
            if !used[i] {
                used[i] = true;
                path.push(nums[i]);
                backtrack(path, res, nums, used);
                path.pop();
                used[i] = false;
            }
        }
    }
    backtrack(&mut Vec::new(), &mut res, &nums, &mut used);
    return res;
}

fn main() {
    println!("{:?}", permute(vec![1, 2, 3]));
    println!("{:?}", permute(vec![0, 1]));
    println!("{:?}", permute(vec![1]));
}

输出：

[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]
[[0, 1], [1, 0]]
[[1]]

**代码2： **字典序法

fn permute(nums: &mut [i32]) -> Vec<Vec<i32>> {
    let mut res = vec![];
    if nums.len() == 1 {
            res.push(nums.to_vec());
            return res;
        }
    nums.sort();
    loop {
        let tmp = nums.to_vec();
        res.push(tmp);
        let (mut i, mut j) = (nums.len() - 2, nums.len() - 1);
        while i > 0 && nums[i] >= nums[i + 1] {
            i -= 1;
        }
        if i == 0 && nums[i] >= nums[i + 1] {
            break;
        }
        while nums[j] <= nums[i] {
            j -= 1;
        }
        nums.swap(i, j);
        nums[i + 1..].reverse();
    }
    res
}

fn main() {
    let mut nums = [1, 2, 3];
    println!("{:?}", permute(&mut nums));
    let mut nums = [0, 1];
    println!("{:?}", permute(&mut nums));
    let mut nums = [1];
    println!("{:?}", permute(&mut nums));
}

**代码3： **DFS

fn permute(nums: Vec<i32>) -> Vec<Vec<i32>> {
    fn dfs(nums: &Vec<i32>, index: usize, p: &mut Vec<i32>, res: &mut Vec<Vec<i32>>, used: &mut Vec<bool>) {
        if index == nums.len() {
            let temp = p.clone();
            res.push(temp);
            return;
        }
        for i in 0..nums.len() {
            if !used[i] {
                used[i] = true;
                p.push(nums[i]);
                dfs(nums, index + 1, p, res, used);
                p.pop();
                used[i] = false;
            }
        }
    }
    if nums.len() == 0 {
        return vec![];
    }
    let mut used: Vec<bool> = vec![false; nums.len()];
    let mut p: Vec<i32> = vec![];
    let mut res: Vec<Vec<i32>> = vec![];
    dfs(&nums, 0, &mut p, &mut res, &mut used);
    return res;
}

fn main() {
    println!("{:?}", permute(vec![1, 2, 3]));
    println!("{:?}", permute(vec![0, 1]));
    println!("{:?}", permute(vec![1]));
}

47. 全排列 II Permutations II

给定一个可包含重复数字的序列 

nums

，按任意顺序 返回所有不重复的全排列。

示例 1：

**输入：**nums = [1,1,2]
**输出：**
[[1,1,2],
 [1,2,1],
 [2,1,1]]

示例 2：

**输入：**nums = [1,2,3]
**输出：**[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

  • 1 <= nums.length <= 8
  • -10 <= nums[i] <= 10

代码1： 回溯法

fn permute_unique(nums: Vec<i32>) -> Vec<Vec<i32>> {
    fn backtrack(path: &mut Vec<i32>, res: &mut Vec<Vec<i32>>, nums: &Vec<i32>, used: &mut Vec<bool>) {
        if path.len() == nums.len() {
            let tmp = path.clone();
            res.push(tmp);
            return;
        }
        for i in 0..nums.len() {
            if used[i] || (i > 0 && !used[i - 1] && nums[i] == nums[i - 1]) {
                continue;
            }
            used[i] = true;
            path.push(nums[i]);
            backtrack(path, res, nums, used);
            path.pop();
            used[i] = false;
        }
    }
    let mut nums_copy = nums.clone();
    nums_copy.sort();
    let mut used: Vec<bool> = vec![false; nums.len()];
    let mut path: Vec<i32> = vec![];
    let mut res: Vec<Vec<i32>> = vec![];
    backtrack(&mut path, &mut res, &nums_copy, &mut used);
    return res;
}
fn main() {
    println!("{:?}", permute_unique(vec![1, 1, 2]));
    println!("{:?}", permute_unique(vec![1, 2, 3]));
}

输出：

[[1, 1, 2], [1, 2, 1], [2, 1, 1]]
[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]

代码2： 字典序法

fn permute_unique(nums: &mut [i32]) -> Vec<Vec<i32>> {
    let mut res = vec![];
    if nums.is_empty() {
        return res;
    }
    nums.sort();
    let len = nums.len();
    let (mut i, mut j) = (len - 2, len - 1);
    loop {
        let tmp = nums.to_vec();
        res.push(tmp);
        while i > 0 && nums[i] >= nums[i + 1] {
            i -= 1;
        }
        if i == 0 && nums[i] >= nums[i + 1] {
            break;
        }
        while j > 0 && nums[j] <= nums[i] {
            j -= 1;
        }
        if nums[j] == nums[i] && j > i + 1 {
            continue;
        }
        nums.swap(i, j);
        nums[i + 1..].reverse();
        if i == 0 && j == 1 {
            break;
        }
        i = len - 2;
        j = len - 1;
    }
    res
}

fn main() {
    let mut nums = [1, 1, 2];
    println!("{:?}", permute_unique(&mut nums));
    let mut nums = [1, 2, 3];
    println!("{:?}", permute_unique(&mut nums));
}

** 代码3：** DFS

fn permute_unique(nums: &mut [i32]) -> Vec<Vec<i32>> {
    let mut res = vec![];
    if nums.is_empty() {
        return res;
    }
    let mut used = vec![false; nums.len()];
    let mut p = vec![];
    nums.sort();
    dfs(nums, 0, &mut p, &mut res, &mut used);
    res
}

fn dfs(nums: &[i32], index: usize, p: &mut Vec<i32>, res: &mut Vec<Vec<i32>>, used: &mut [bool]) {
    if index == nums.len() {
        res.push(p.clone());
        return;
    }
    for i in 0..nums.len() {
        if !used[i] {
            if i > 0 && nums[i] == nums[i - 1] && !used[i - 1] {
                continue;
            }
            used[i] = true;
            p.push(nums[i]);
            dfs(nums, index + 1, p, res, used);
            p.pop();
            used[i] = false;
        }
    }
}

fn main() {
    let mut nums = [1, 1, 2];
    println!("{:?}", permute_unique(&mut nums));
    let mut nums = [1, 2, 3];
    println!("{:?}", permute_unique(&mut nums));
}

fn permute_unique(nums: Vec<i32>) -> Vec<Vec<i32>> {
    fn dfs(nums: &[i32], index: usize, p: &mut Vec<i32>, res: &mut Vec<Vec<i32>>, used: &mut [bool]) {
        if index == nums.len() {
            res.push(p.clone());
            return;
        }
        for i in 0..nums.len() {
            if !used[i] {
                if i > 0 && nums[i] == nums[i - 1] && !used[i - 1] {
                    continue;
                }
                used[i] = true;
                p.push(nums[i]);
                dfs(nums, index + 1, p, res, used);
                p.pop();
                used[i] = false;
            }
        }
    }
    if nums.is_empty() {
        return vec![];
    }
    let mut nums_copy = nums.clone();
    nums_copy.sort();
    let mut res: Vec<Vec<i32>> = vec![];
    let mut used = vec![false; nums.len()];
    dfs(&nums_copy, 0, &mut vec![], &mut res, &mut used);
    res
}

fn main() {
    println!("{:?}", permute_unique(vec![1, 1, 2]));
    println!("{:?}", permute_unique(vec![1, 2, 3]));
}

48. 旋转图像 Rotate Image

给定一个 *n *× n 的二维矩阵 

matrix

表示一个图像。请你将图像顺时针旋转 90 度。

你必须在
原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。**请不要 **使用另一个矩阵来旋转图像。

示例 1：

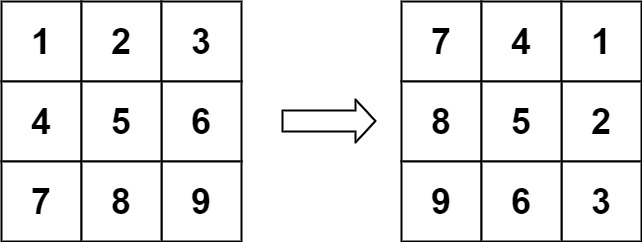
**输入：**matrix = [[1,2,3],[4,5,6],[7,8,9]]
**输出：**[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

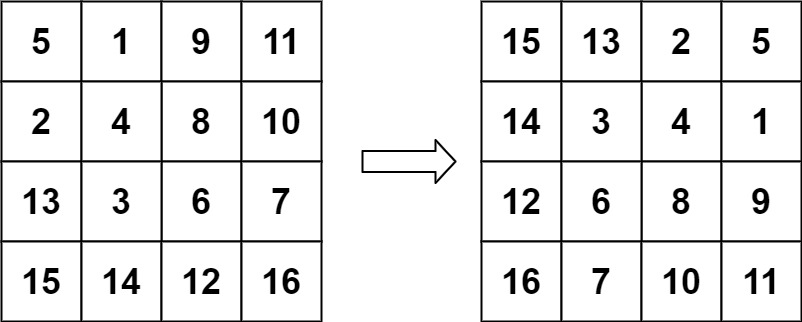
**输入：**matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
**输出：**[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

  • n == matrix.length == matrix[i].length
  • 1 <= n <= 20
  • -1000 <= matrix[i][j] <= 1000

**代码1： **转置加翻转

先转置矩阵，然后翻转每一行即可得到顺时针旋转 90 度后的矩阵。

fn rotate(matrix: &mut Vec<Vec<i32>>) {
    let n = matrix.len();
    // 转置矩阵
    for i in 0..n {
        for j in i..n {
            let temp = matrix[i][j];
            matrix[i][j] = matrix[j][i];
            matrix[j][i] = temp;
        }
    }
    // 翻转每一行
    for i in 0..n {
        for j in 0..n / 2 {
            let temp = matrix[i][j];
            matrix[i][j] = matrix[i][n - j - 1];
            matrix[i][n - j - 1] = temp;
        }
    }
}

fn main() {
    let mut matrix = vec![vec![1, 2, 3], vec![4, 5, 6], vec![7, 8, 9]];
    rotate(&mut matrix);
    println!("{:?}", matrix);
    let mut matrix = vec![vec![5, 1, 9, 11], vec![2, 4, 8, 10], vec![13, 3, 6, 7], vec![15, 14, 12, 16]];
    rotate(&mut matrix);
    println!("{:?}", matrix);
}

输出：

[[7, 4, 1], [8, 5, 2], [9, 6, 3]]
[[15, 13, 2, 5], [14, 3, 4, 1], [12, 6, 8, 9], [16, 7, 10, 11]]

**代码2： **分块翻转

将矩阵分成四个部分，并将每个部分按顺时针旋转 90 度。

fn rotate(matrix: &mut Vec<Vec<i32>>) {
    let n = matrix.len();
    // 转置矩阵
    for i in 0..n {
        for j in i..n {
            let temp = matrix[i][j];
            matrix[i][j] = matrix[j][i];
            matrix[j][i] = temp;
        }
    }
    // 翻转每一行
    for i in 0..n {
        for j in 0..n / 2 {
            let temp = matrix[i][j];
            matrix[i][j] = matrix[i][n - j - 1];
            matrix[i][n - j - 1] = temp;
        }
    }
}

fn main() {
    let mut matrix = vec![vec![1, 2, 3], vec![4, 5, 6], vec![7, 8, 9]];
    rotate(&mut matrix);
    println!("{:?}", matrix);
    let mut matrix = vec![vec![5, 1, 9, 11], vec![2, 4, 8, 10], vec![13, 3, 6, 7], vec![15, 14, 12, 16]];
    rotate(&mut matrix);
    println!("{:?}", matrix);
}

**代码3： **对角线变换+水平翻转

将矩阵分成四个部分，并将每个部分按顺时针旋转 90 度。

fn rotate(matrix: &mut Vec<Vec<i32>>) {
    let row = matrix.len();
    if row <= 0 {
        return;
    }
    let column = matrix[0].len();
    // 对角线变换
    for i in 0..row {
        for j in i + 1..column {
            let temp = matrix[i][j];
            matrix[i][j] = matrix[j][i];
            matrix[j][i] = temp;
        }
    }
    // 竖直轴对称翻转
    let half_column = column / 2;
    for i in 0..row {
        for j in 0..half_column {
            let temp = matrix[i][j];
            matrix[i][j] = matrix[i][column - j - 1];
            matrix[i][column - j - 1] = temp;
        }
    }
}

fn main() {
    let mut matrix = vec![vec![1, 2, 3], vec![4, 5, 6], vec![7, 8, 9]];
    rotate(&mut matrix);
    println!("{:?}", matrix);
    let mut matrix = vec![vec![5, 1, 9, 11], vec![2, 4, 8, 10], vec![13, 3, 6, 7], vec![15, 14, 12, 16]];
    rotate(&mut matrix);
    println!("{:?}", matrix);
}

翻转+旋转原理C代码

/*

  • clockwise rotate 顺时针旋转
  • first reverse up to down, then swap the symmetry
  • 1 2 3 7 8 9 7 4 1
  • 4 5 6 => 4 5 6 => 8 5 2
  • 7 8 9 1 2 3 9 6 3

/
void rotate(vector<vector<int> > &matrix) {
reverse(matrix.begin(), matrix.end());
for (int i = 0; i < matrix.size(); ++i) {
for (int j = i + 1; j < matrix[i].size(); ++j)
swap(matrix[i][j], matrix[j][i]);
}
}
/

  • anticlockwise rotate 逆时针旋转
  • first reverse left to right, then swap the symmetry
  • 1 2 3 3 2 1 3 6 9
  • 4 5 6 => 6 5 4 => 2 5 8
  • 7 8 9 9 8 7 1 4 7

*/
void anti_rotate(vector<vector<int> > &matrix) {
for (auto vi : matrix) reverse(vi.begin(), vi.end());
for (int i = 0; i < matrix.size(); ++i) {
for (int j = i + 1; j < matrix[i].size(); ++j)
swap(matrix[i][j], matrix[j][i]);
}
}

🌟 每日一练刷题专栏 🌟

✨持续，努力奋斗做强刷题搬运工！

👍 点赞，你的认可是我坚持的动力！

🌟 收藏，你的青睐是我努力的方向！

✎ 评论，你的意见是我进步的财富！

☸ 主页：https://hannyang.blog.csdn.net/

Rust每日一练 专栏

（2023.5.16~）更新中...

Golang每日一练 专栏

（2023.3.11~）更新中...

Python每日一练 专栏

（2023.2.18~2023.5.18）暂停更

C/C++每日一练 专栏

（2023.2.18~2023.5.18）暂停更

Java每日一练 专栏

（2023.3.11~2023.5.18）暂停更

标签： rust leetcode 回溯法
本文转载自: https://blog.csdn.net/boysoft2002/article/details/130956060
版权归原作者 Hann Yang 所有， 如有侵权，请联系我们删除。
登录后发布评论

“Rust每日一练(Leetday0016) 全排列I\II、旋转图像”的评论:

还没有评论
关于作者
...
overfit同步小助手
文章同步
相关阅读

如何给SaaS应用做安全

【软件测试】自动化常用函数

postman变量和脚本功能介绍

Python Selenium常见的报错以及措施

idea导出配置文件

如何在visual studio中 生成 并 使用dll和lib文件

Docker homeassistant 反向代理 外网访问

文章导航