把数组排成最小的数_数组中的逆序对(归并统计法)_数字在升序数组中出现的次数_丑数(剑指offer)

排序

把数组排成最小的数

题目链接

importjava.util.*;publicclassSolution{publicStringPrintMinNumber(int[] numbers){//空数组的情况if(numbers ==null|| numbers.length ==0)return"";String[] nums =newString[numbers.length];//将数字转成字符for(int i =0; i < numbers.length; i++)
            nums[i]= numbers[i]+"";//按照重载排序Arrays.sort(nums,newComparator<String>(){publicintcompare(String s1,String s2){return(s1 + s2).compareTo(s2 + s1);}});StringBuilder res =newStringBuilder();//字符串叠加for(int i =0; i < nums.length; i++)
            res.append(nums[i]);return res.toString();}}

• 这里题目重点就是自己设计一个排序,通过Comparator接口!
• 字符串拼接s1 + s21>s2 + s1说明s1和s2位置需要交换!

相似题目:数据流中的中位数

读懂题意!

importjava.util.*;publicclassSolution{//将数据流保存在table中!privateArrayList<Integer> table =newArrayList<>();publicvoidInsert(Integer num){//在table数据流中插入num值!if(table.isEmpty()){//直接尾插
            table.add(num);}else{//不为空,找到合适位置插入!升序排序!int i =0;for(i =0;i< table.size();i++){if(table.get(i)>num){//找到了合适位置!
                    table.add(i,num);break;}}if(i==table.size()){//尾插!
                table.add(i,num);}}}publicDoubleGetMedian(){//计算中位数!if(table.isEmpty()){return0.0;}else{int size = table.size();if(size%2==0){//偶数!return(double)(table.get(size/2)+table.get(size/2-1))/2;}else{//奇数return(double)table.get(size/2);}}}}

• 插入考虑边界问题!

数组中的逆序对(归并统计法)

题目链接

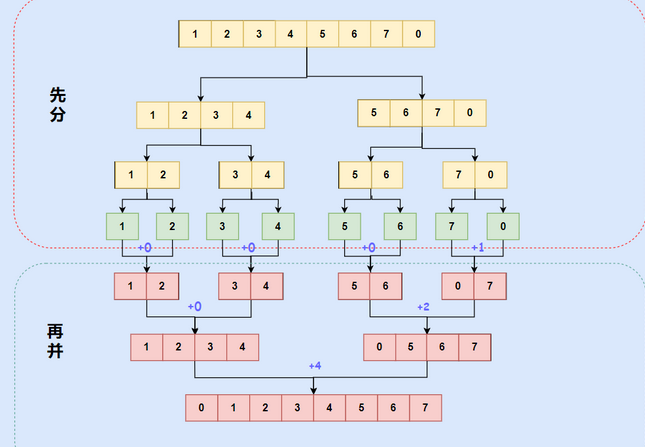
publicclassSolution{privateint sum =0;//保存结果值!publicintInversePairs(int[] array){//归并统计法!//采用归并排序的思想,在毕竟合并时统计逆序对的组数!if(array.length<2){//无逆序队return0;}//进行归并统计!mergeSort(array,0,array.length-1);return sum;}publicvoidmergeSort(int[] array,int left,int right){//进行先分!int mid = left +(right-left)/2;if(left<right){//左区间!mergeSort(array,left,mid);//右区间!mergeSort(array,mid+1,right);//后和并merge(array,left,mid,right);}}publicvoidmerge(int[] array,int left,int mid,int right){//我们进行合并时需要有个临时数组保存int[] tmp =newint[right-left+1];//记录临时数组开始下标位置!int tmpIndex =0;//记录原数组开始下标位置(临时数组数据需要放入到原数组中)int arrayIndex = left;//左区间开始位置!int l = left;//右区间开始位置!int r = mid+1;//进行比较合并!while(l<=mid&&r<=right){if(array[l]<=array[r]){//无逆序,直接将l下标保存在临时数组!
               tmp[tmpIndex++]= array[l++];}else{//逆序,交换(就将r下标位置保存)
               tmp[tmpIndex++]= array[r++];//记录逆序对数!//进行归并时,左右数组已经分别有序!//l大于r下标元素,也就是l到mid区间都大于r下标元素//所以逆序对数为 l下标位置到 r位置个数!
               sum += mid - l +1;
               sum %=1000000007;}}//区间长度不相等,有剩余值!while(l<=mid){
            tmp[tmpIndex++]= array[l++];}while(r<=right){
            tmp[tmpIndex++]= array[r++];}//将元素放回到原数组!for(int x : tmp){
            array[arrayIndex++]= x;}}}

数字在升序数组中出现的次数

题目链接

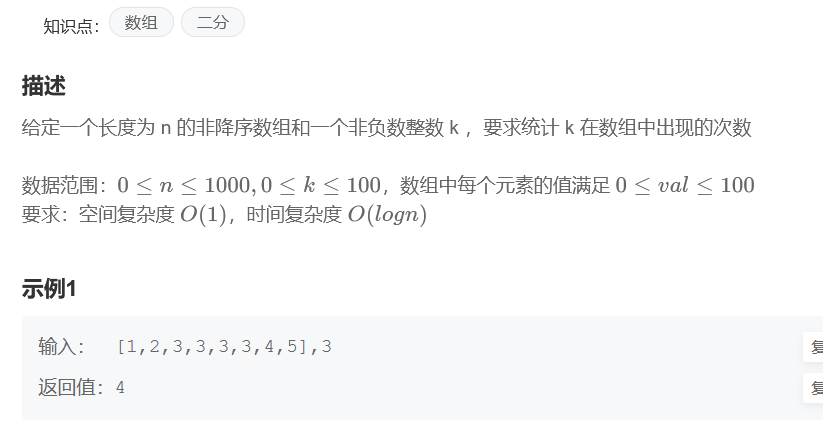
publicclassSolution{publicintGetNumberOfK(int[] array ,int k){//数组以有序!//二分查找!int l =0,r = array.length-1;int mid = l +(r-l)/2;boolean flg =false;while(l<=r){
            mid = l +(r-l)/2;if(array[mid]>k){//定位在左区间!
                r = mid-1;}elseif(array[mid]<k){//定位在右区间!
                l = mid+1;}else{//相等!//找到!
                flg =true;break;}}if(flg){for(int i = l;i<=mid;i++){if(array[i]==k){//相等区间左边界!
                    l = i;break;}}for(int i = r;i>=mid;i--){if(array[i]==k){//相等区间右边界!
                    r = i;break;}}return r - l +1;}return0;}}

publicclassSolution{publicintGetNumberOfK(int[] array ,int k){//直接找到边界,[left,right) 左闭右开!returnbisearch(array,k+0.5)-bisearch(array,k-0.5);}publicintbisearch(int[] array,double k){int left =0,right = array.length-1;while(left<=right){int mid = left +(right-left)/2;if(array[mid]<k){
                left = mid +1;}else{
               right = mid -1;}}//这里二分如果没找到返回的是大于该值的一个下标return left;}}

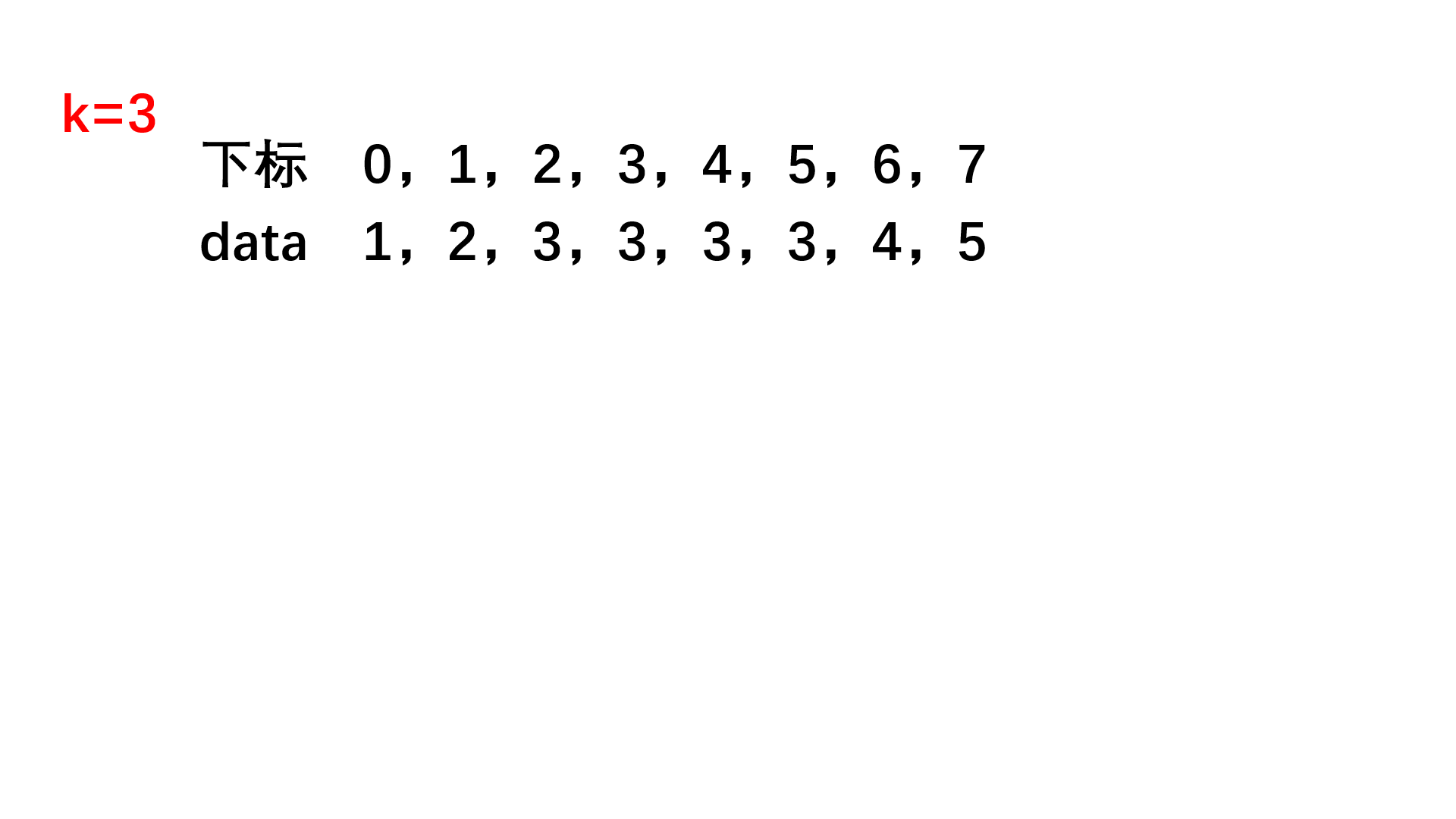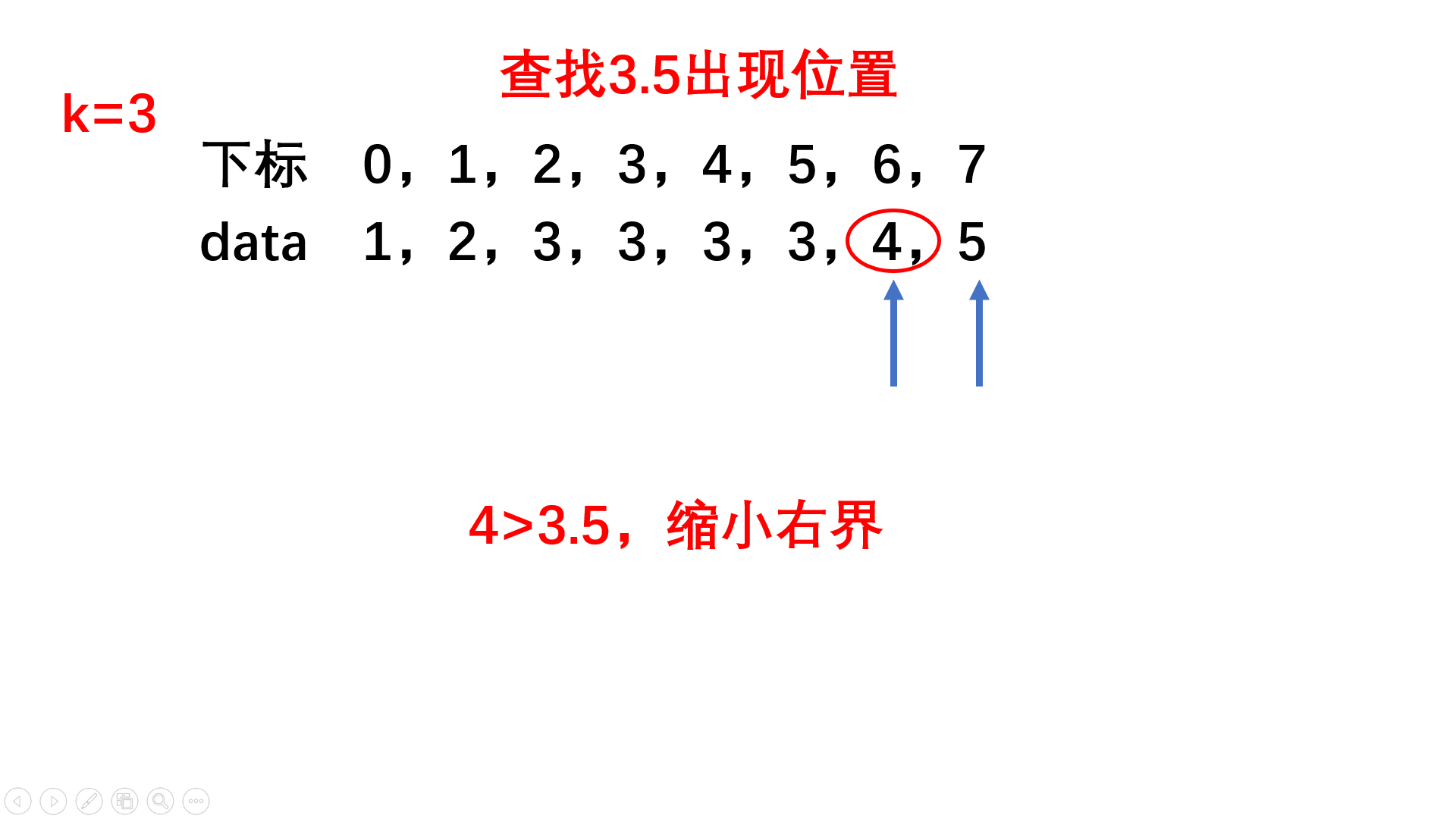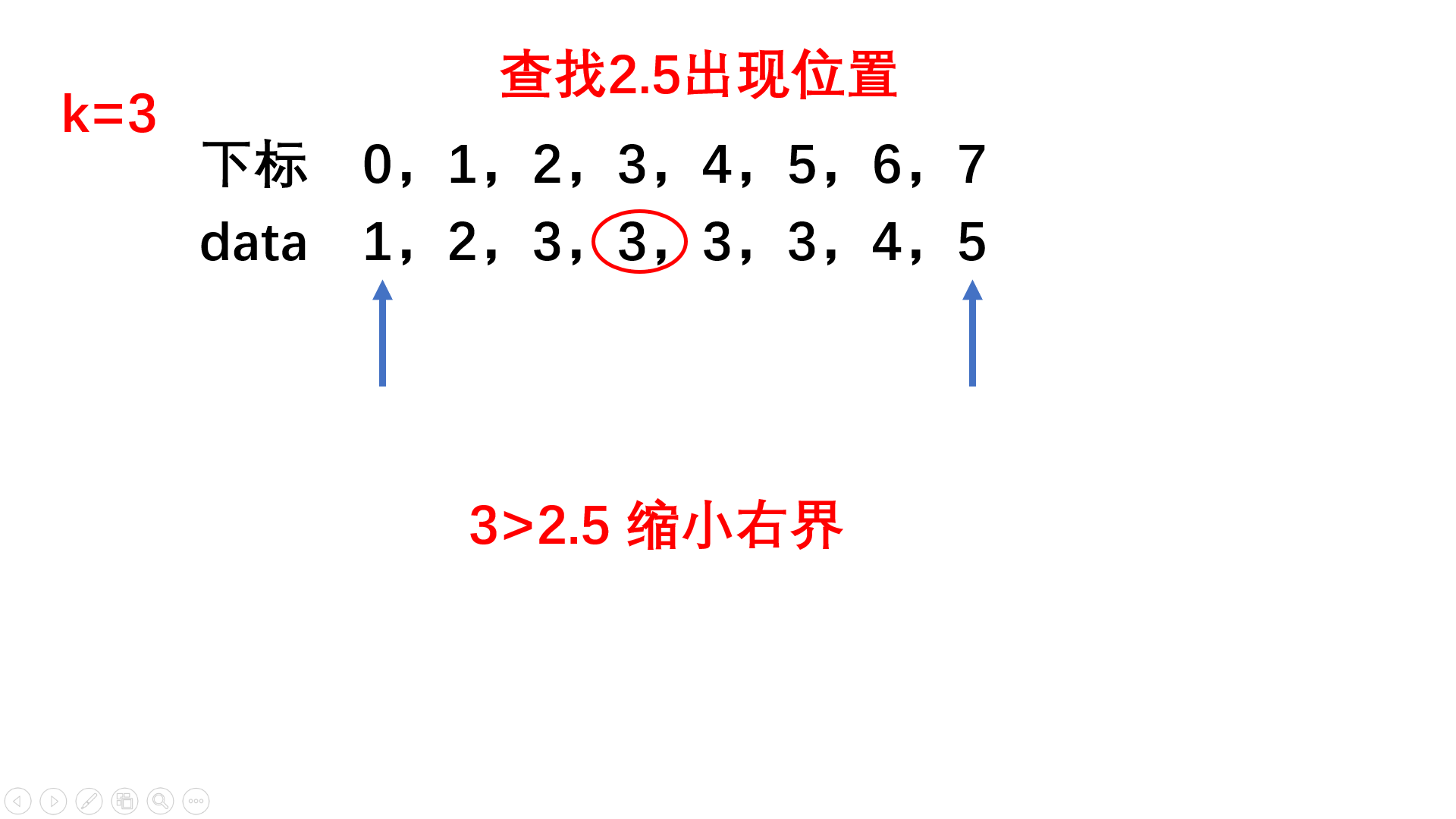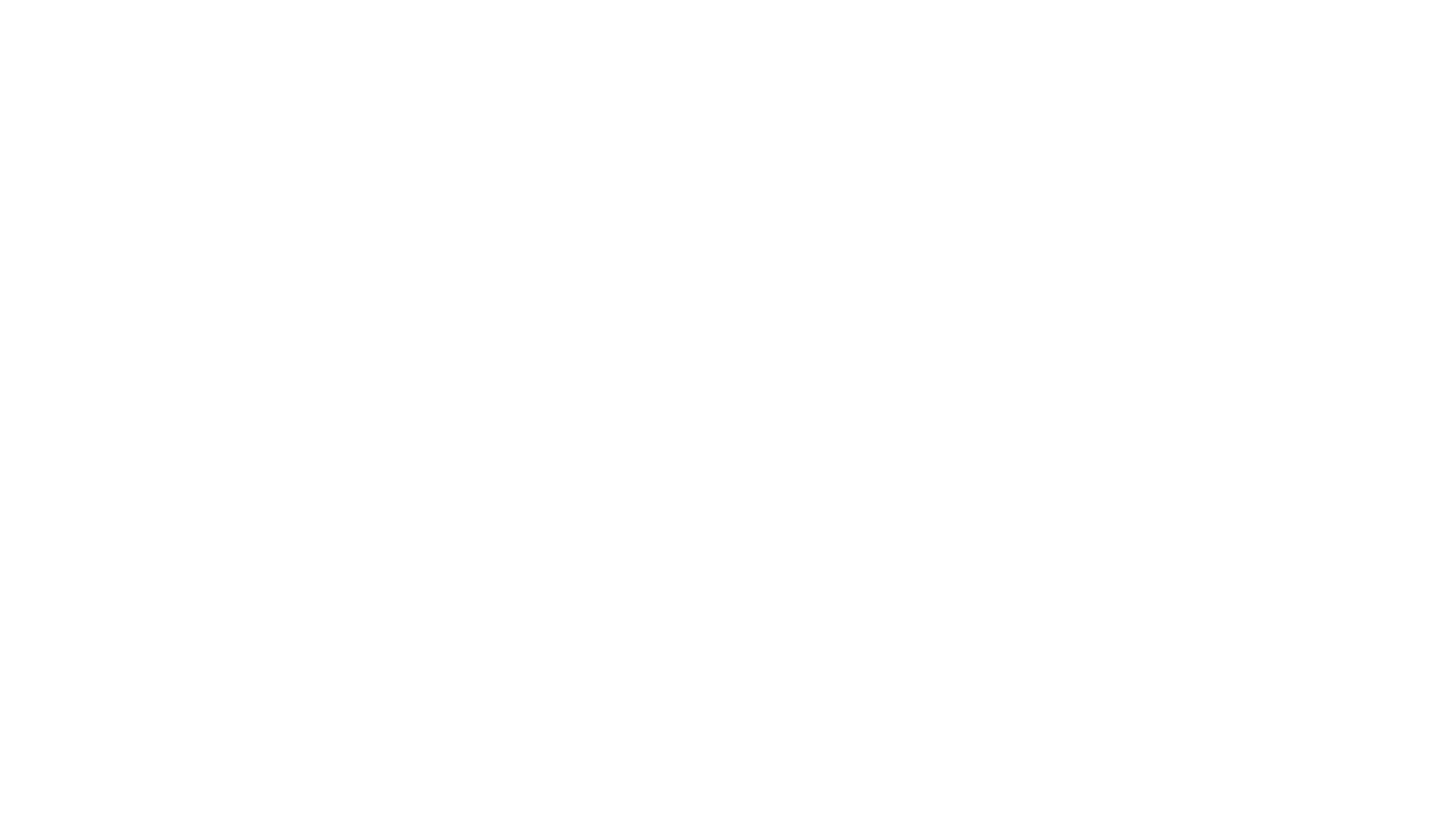
丑数

链接

解题思路：

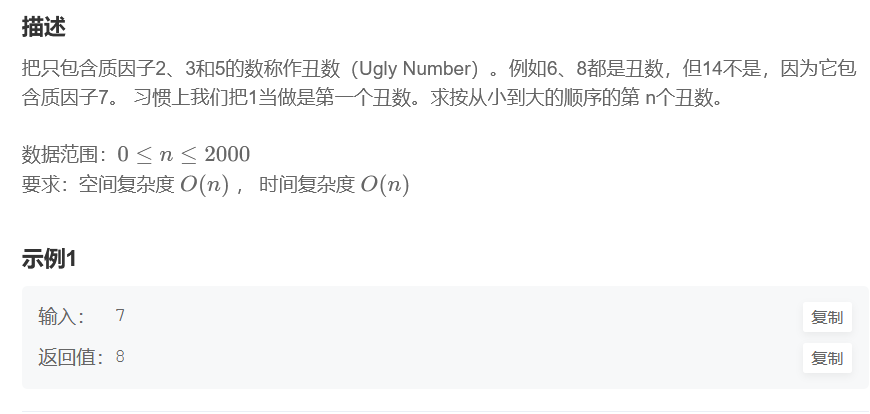
我们先看到题目，把只包含质因子2、3和5的数称作丑数（Ugly Number）。例如6、8都是丑数，但14不是，因为它包含质因子7。 习惯上我们把1当做是第一个丑数。

有了上面的定义我们就可以知道，丑数的形式就是2x3y5^z
所以我们可以定义一个数组res，存储第n个丑数。
因为我们要将丑数按从小到大的顺序排序，所以我们就得将对应的丑数放在对应的下标位置，小的放前面。
因为最小的丑数就是1，所以我们初始化res[0]=1，那么接下来的一个丑数是什么呢？我们自己知道是2。
但是我们能不能有一个格式，去将得到接下来的丑数是谁呢？
这个时候上面我们的出来的丑数的格式就起作用了，丑数的形式无非就是这样2x3y5z
所以我们就将res[n]去乘以 2、3、5，然后比较出最小的那个，就是我们当前的下一个丑数了。

publicclassSolution{publicintGetUglyNumber_Solution(int index){if(index==0){return0;}//利用 丑数: 2^x*3^y*5^z!int[] arr =newint[index];//保存前index丑数值!
        arr[0]=1;int i2 =0,i3 =0,i5 =0;//记录2/3/5分别相乘的次数!for(int i =1;i<index;i++){//将3个中最小丑数放在前面!//每次都是求出最小的丑数!
            arr[i]=Math.min(arr[i2]*2,Math.min(arr[i3]*3,arr[i5]*5));if(arr[i]==arr[i2]*2){//说明这里的 2 相乘次数加一!
                i2++;}if(arr[i]==arr[i3]*3){//说明这里的 3 相乘次数加一!
                i3++;}if(arr[i]==arr[i5]*5){//说明这里的 5 相乘次数加一!
                i5++;}}return arr[index-1];}}