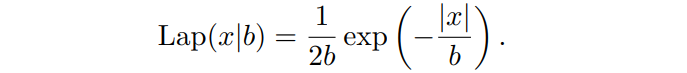1.前言(如何实现差分隐私)
差分隐私是通过随机化的方式来干扰正常的查询,或是对数据集做一些处理. 那么最常规的干扰查询/处理数据的手法,就是加噪音。
一般情况下,数据库的查询可分为两类:数值查询和非数值查询。
1.数值查询:小明的高数考了多少分?
2.非数值查询:小明分最高的是哪一门课?
应对这两种查询,分别有拉普拉斯机制和指数机制。
2.拉普拉斯噪声
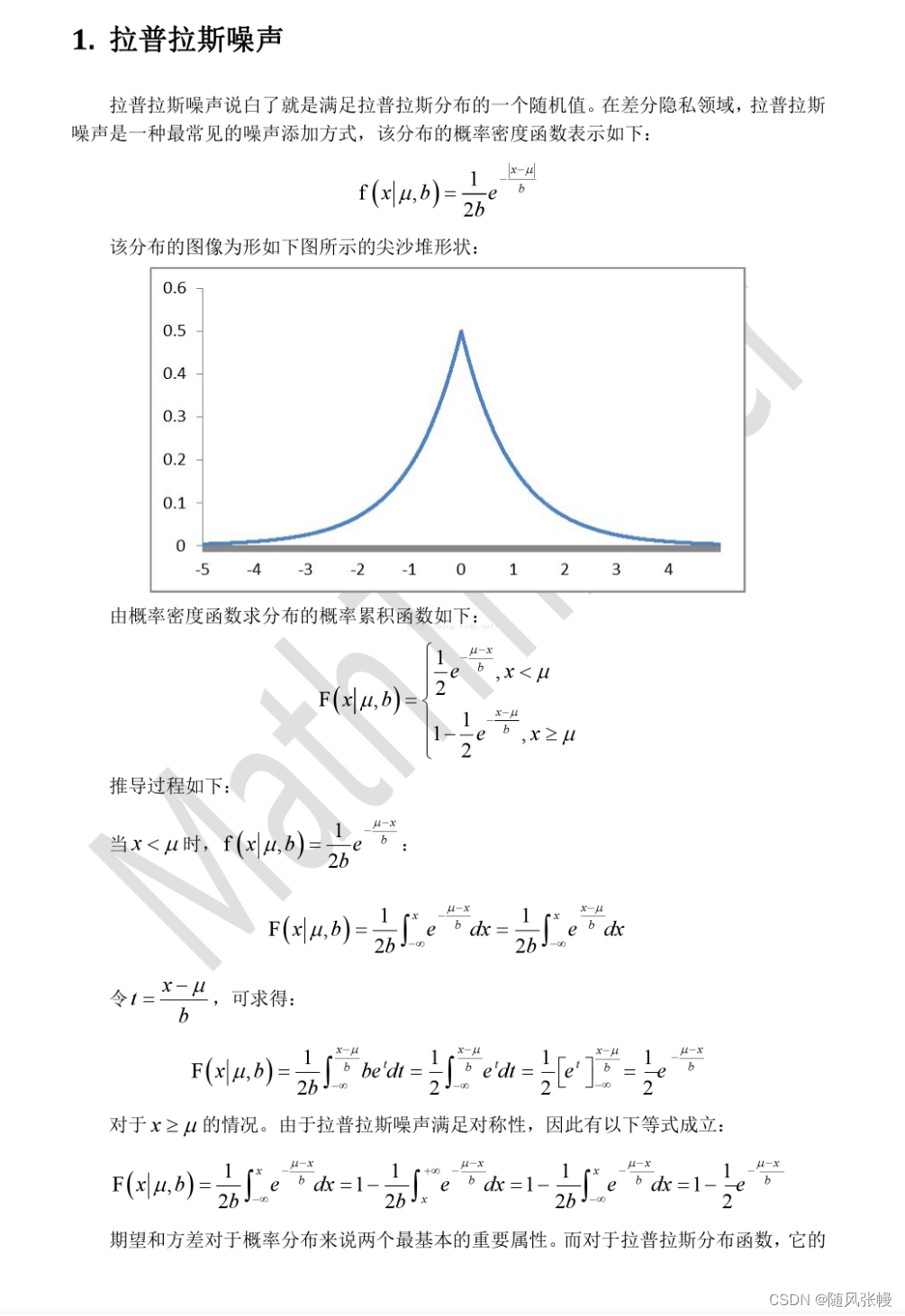

3.拉普拉斯机制
拉普拉斯机制主要是针对数值型的查询,即
:
映射数据库为k个实数。因此遇到发布数值型数据的时候,可以用拉普拉斯机制来引入噪声
首先,我们应该考虑这个查询的结果有多依赖于某个特定病人的信息
一般我们使用
来衡量这个依赖程度,
可以用来控制噪声的幅度,如果
比较大,那相应的噪声的幅度就应该大一些,才能有更好的隐私保证。
可以是全局敏感度,也可以是局部敏感度,使用全局敏感度还是局部敏感度取决于实际情况:
全局敏感度一般较大,如果全局敏感度大小可以接受,那我们可以使用全局敏感度;如果全局敏感度过大,我们使用局部敏感度。局部敏感度会与数据分布有很强的关联, 故在需要使用局部敏感度时,常采用局部敏感度的平滑上界.
注:全局敏感度和局部敏感度后面会讲
其次,我们可以往查询结果中加入一个服从拉普拉斯分布的噪声
拉普拉斯机制简单地来说就是在
的
个实数输出上,加上噪声。加入的噪声,就是在拉普拉斯分布上采样。拉普拉斯分布是一个连续分布,这里只考虑均值为 0 的拉普拉斯分布。尺度参数为 b 的拉普拉斯分布记为
,其密度函数为:
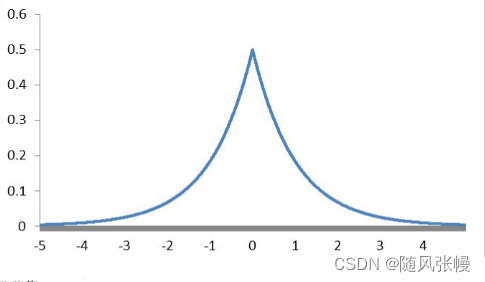
噪声分布如下图所示,该函数中值当x=0时,
为最大,两边成指数型下降;
当尺度参数
=
时(
为全局敏感度或局部敏感度),即能满足
-差分隐私
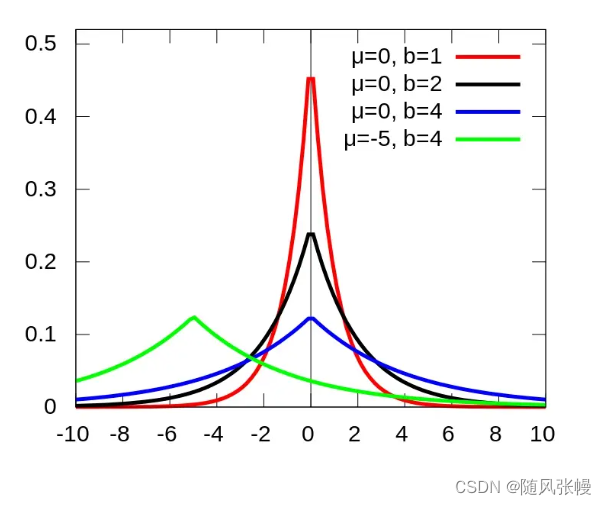
可以看出,在隐私预算
不变的情况下,敏感度
越大,则尺度参数
越大,尺度参数
越大,则加入的噪声越大,如下图所示
拉普拉斯机制:
给任意函数
:
,拉普拉斯机制定义为:
其中
是从
~
采样的独立同分布的随机变量
4.拉普拉斯噪声满足ε-差分隐私定义



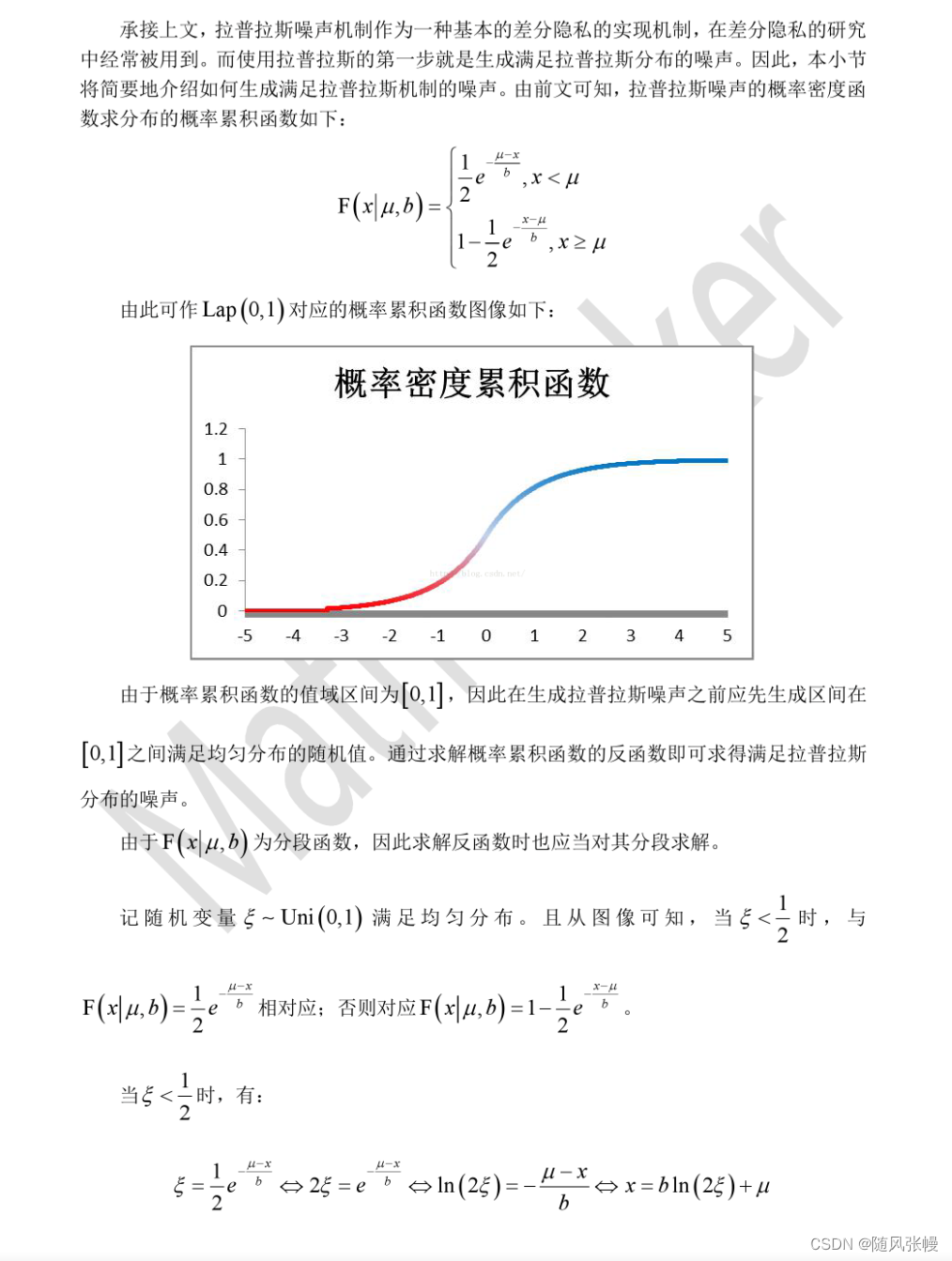
5.拉普拉斯噪声的生成

版权归原作者 随风张幔 所有, 如有侵权,请联系我们删除。