【阿一网络安全】如何让你的密码更安全？（二） - 非对称加密

上次《【阿一网络安全】如何让你的密码更安全？(一) - 对称加密》提到加密算法的对称加密，我们这次来聊聊非对称加密。

和对称加密不同，非对称加密的加密密钥和解密密钥不同。

非对称加密

大概过程就是，发送方使用公钥对明文数据进行加密，把密文发送给接收方，接收方收到密文，用私钥进行解密。如图所示：

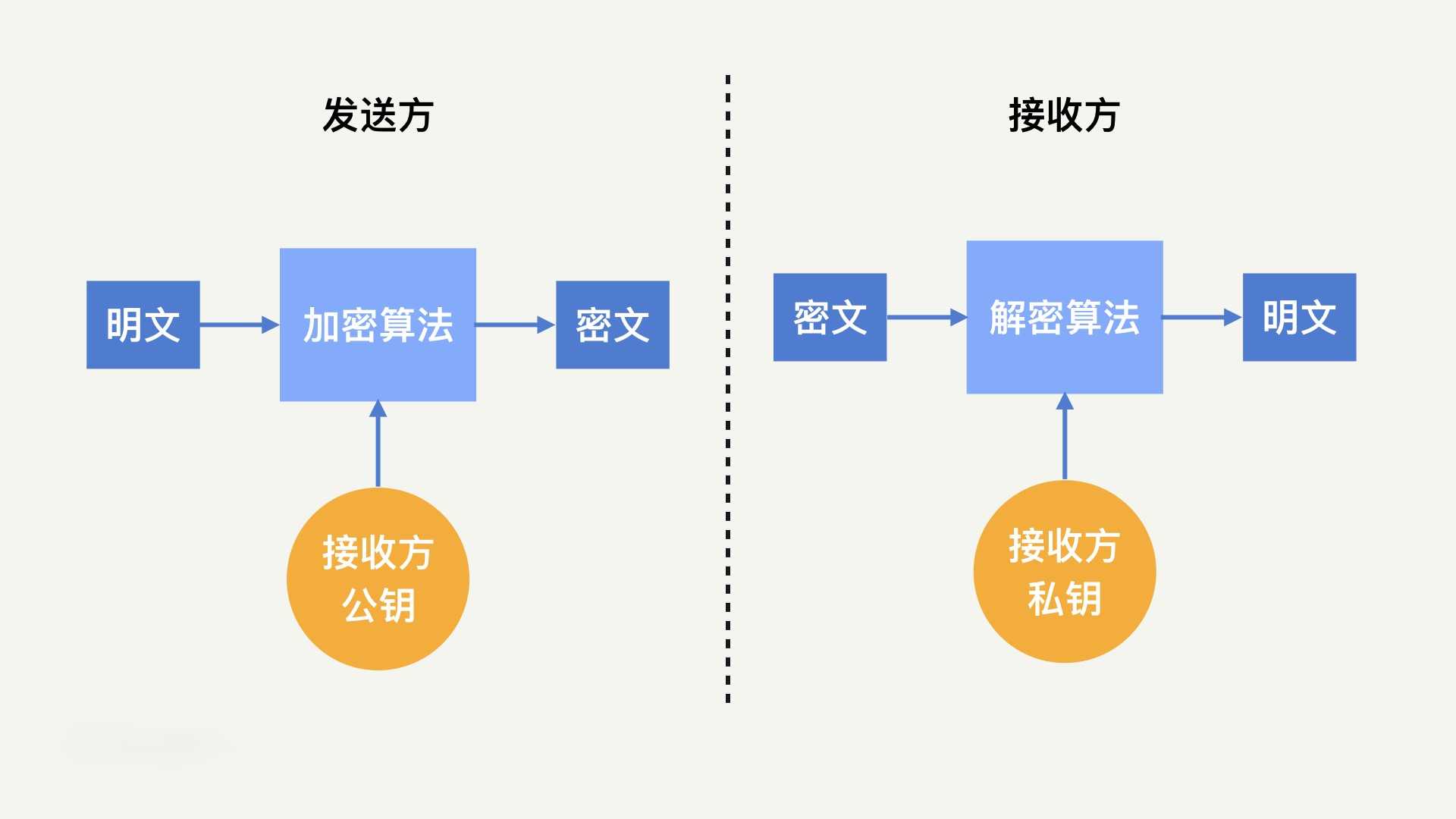
在我们使用对称加密的时候，不仅要约定好发送、接收方的密钥，还要担心密钥泄漏。而在非对称加密中，不需要担心这个问题，公钥本身就是公开的，不需要额外对其进行保密，可以把公钥发给所有需要的人。

非对称加密，除了加密功能之外，部分非对称算法还提供了签名功能（确保明文数据的完整性和真实性，并不是保密性）。

发送方用私钥对明文数据进行加密,得到签名。接收方收到明文数据和签名后，用发送方的公钥解密签名，并将结果与明文数据比对。如果匹配，就证明这段消息确实是发送方发送的且没有被篡改。

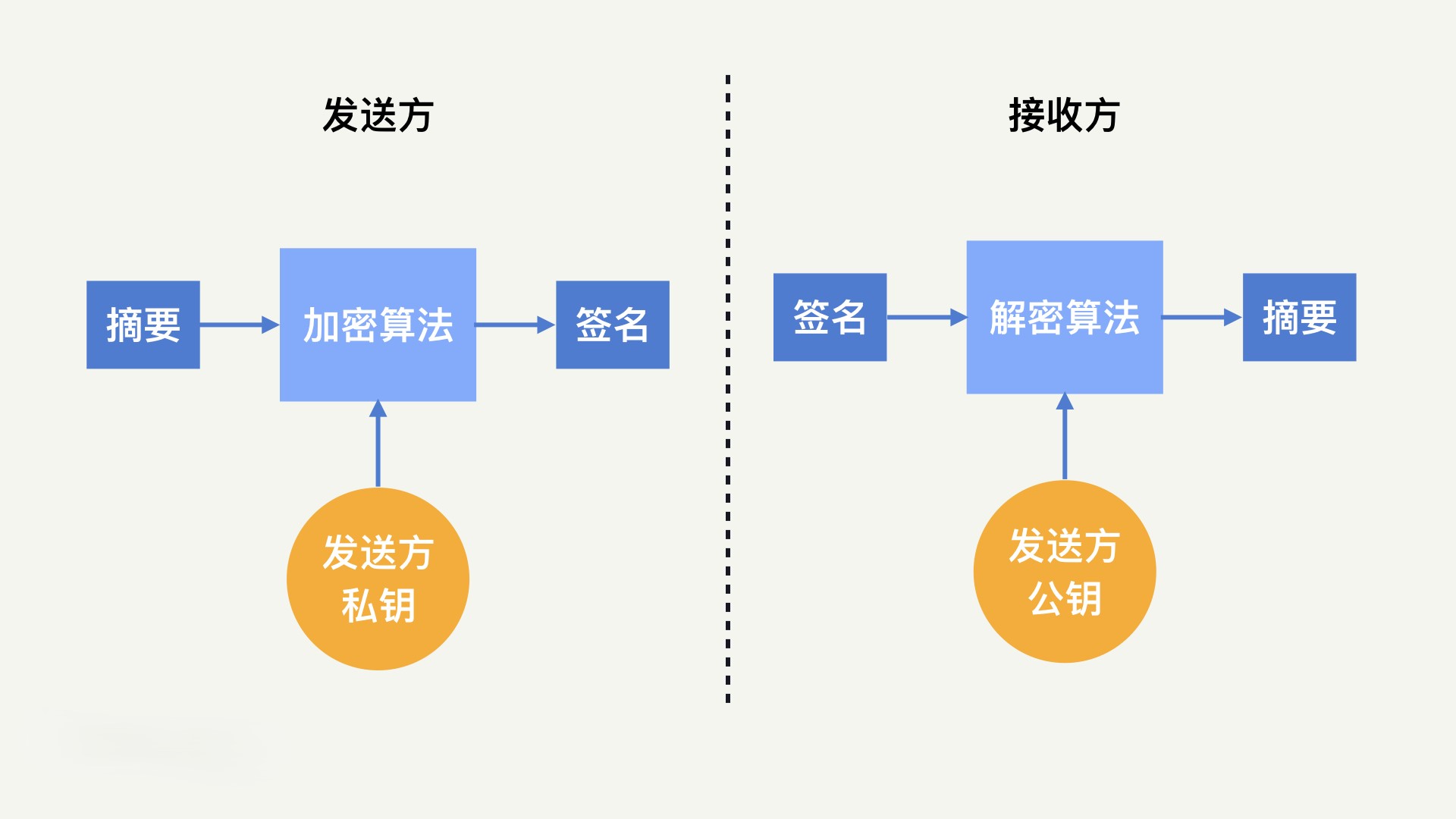
非对称加密的核心思想，是基于特定的数学难题设计的，特点就是：

1. 正向计算容易
2. 反向计算在计算上不可行（在合理的时间内无法完成）

经典且广泛使用的非对称加密算法包括这几种，RSA、ECC和国密的SM2。

RSA

RSA是一种非对称加密算法，在公开密钥加密和电子商业中被广泛使用，是由 Ron Rivest、Adi Shamir 和Leonard Adleman 三人一起提出，RSA就是他们三人姓氏的首字母组成。

RSA的安全性，基于 大整数因子分解 的数据难题，换言之，对一极大整数做因数分解愈困难，RSA 算法愈可靠。它使用两个不同的密钥进行加密，公钥用于加密，私钥用于解密。

密钥的生成

公钥和私钥，都是由 发送方 约定并生成的。

1. 选择两个大的质数 p 和 q，p ≠ q，计算 N = p * q
2. 计算欧拉函数 φ(N) = φ§ * φ(q) = (p - 1) * (q - 1)
3. 选择一个小于 φ(N) 的整数 e，使得 e 与 φ(n) 互质
4. 计算 e 关于 φ(N) 的模逆元 d，使得 d * e ≡ 1(mod φ(N))

公钥 = (N, e)。

私钥 = (N, d)。

加密

c = me mod N

假设发送方想把明文 m 发送给接收方，就可以按照这个公式把 明文 m，加密成 密文 c 发送给接收方。

解密

m = cd mod N

与加密类似，接收方获取到 密文 c，可以按照这个公式 把 密文 c，解密成 明文 m。

数字签名

RSA也可以用作 数字签名。

接收方 想给 发送方 发消息的话，可以把 他想要发的消息明文计算一个 散列值（Message Digest），然后用私钥 加密 这个 散列值 并放在消息明文后一起发送给发送方。

发送方 收到 接收方发送的消息后，把密文用 公钥 进行解密，然后和 发送发自己对这个 消息明文 的计算的散列值相比较，如果二者一致的话，那么就可以确保该消息 是接收方发送的，并且没有被篡改过。

安全性

• 安全性基于 大整数因子分解的困难性。
• 密钥长度 一般为 2048 或 4096 位。目前推荐的长度至少位 2048位。

优缺点

优点：

• 原理相对简单
• 可用于加密，也可用于数字签名
• 广泛使用

缺点：

• 计算速度慢
• 可能受到量子计算机的威胁

实际应用

• HTTPS 协议
• SSH 安全连接
• 数字证书

虽然RSA的理论基础相对简单，但是实际使用过程中，需要考虑很多的细节，比如填充方案，密钥管理，性能优化等。

ECC

ECC（椭圆曲线密码学，Elliptic Curve Cryptography)，是一种基于椭圆曲线数学的公开密钥加密算法。

对比RSA的主要优势在于，使用较小的密钥长度就能提供相当级别的安全性，使得它特别适合资源受限的环境下使用，比如移动设备和物联网设备。

ECC 的安全性，基于椭圆曲线离散对数问题（ECDLP）的困难性，在椭圆曲线上，已知点P 和 点Q，找到整数k使得 Q = kP 是困难的。

密钥的生成

1. 选择椭圆曲线 E 和 基点 G
2. 选择 私钥 d （随机大整数）
3. 计算 公钥 Q = dG

加密

1. 选择随机数 r
2. 计算 R = rG 和 S = rQ
3. 使用 S 的 x坐标 作为对称密钥 加密

解密

1. 计算 S = dR
2. 使用 S 的 x坐标 作为对称密钥 解密

数字签名

签名：

• 选择随机数 k
• 计算 R = kG，r 为 R 的 x坐标
• 计算 s = k-1 (H(m) + dr) mod n
• 签名为 (r, s)

验证：

• 计算 u1 = H(m)s-1 mod n 和 u2 = rs-1 mod n
• 计算 V = u1G + u2Q
• 如果 V 的x坐标等于r，则签名正确

安全性

• 基于 椭圆曲线离散对数问题的困难性
• 密钥最小长度为 224位，对应的对称加密密钥的长度为 128位

优缺点

优点：

• 使用更短的密钥获得相同的安全性，最小224位
• 计算速度更快
• 资源耗费低

缺点：

• 量子计算攻击
• 无效曲线攻击
• 后门
• 旁路攻击

实际应用

• TLS / SSL
• 移动设备安全
• 物联网设备
• 加密货币

虽然ECC的数学基础看起来更复杂，但是他的计算效率更加的高效。它的高效性使得它广泛用于许多加密货币中。实现过程中仍然需要注意一下细节，比如曲线的选择、随机数的生成等。

SM2

SM2是我国国家密码管理局发布的一种公钥密码算法，属于国家商用密码，算法公开。

它基于ECC（椭圆曲线密码学），但有其特定的参数和实现细节，加密强度和ECC相当。

密钥的生成

1. 生成随机数 *d ∈ [1, n-1]*，其中 n 是椭圆曲线的阶
2. 计算 公钥 P = dG ，G为基点

加密

1. 生成随机数 k ∈ [1, n-1]
2. 计算点，*(x1, y1) = kG，(x2, y2) = kP*，P为接收方公钥
3. 使用对称加密算法 SM4加密消息，密钥为 x2
4. 然后加密明文

解密

1. 计算点，*(x2, y2) = d(x1, y2)*，d为接收方私钥
2. 使用对称加密算法 SM4解密密文，密钥 为 x2

数字签名

签名：

1. 对 消息 M进行摘要处理（SM3），得到 e = H(M)，H为哈希函数
2. 生成随机数 k ∈ [1, n-1]
3. 计算点，*(x1, y1) = kG*
4. 计算 r，r = (e + x1) mod n，如果 r = 0 或者 r + k = n，则重新选择 k
5. 计算 s，s = ((1 + d)-1 * (k - r * d)) mod n，如果 s = ，则重新选择 k
6. 签名为 (r, s)

验证：

1. 检查 r，s ∈ [1, n-1]
2. 计算 e，e = H(M)
3. 计算 t，t = (r + s) mod n，如果 t = 0，则签名无效
4. 计算点，(x1, y1) = sG + tP
5. 计算 R，R = (e + x1) mod n，如果 R = r，则签名有效，否则签名无效

安全性

• 采用256的椭圆曲线
• 不可伪造、不可否认性
• 有效防止中间人攻击
• 前向安全性，即使长期泄露密钥，也不会影响之前会话的安全性

优缺点

优点：

• 基于ECC，使用更短的密钥获得相同的安全性
• 效率高
• 为我国国家密码管理局发布的标准算法，具有良好的兼容性和标准化支持
• 不仅支持加解密，还支持数字签名，能够满足多种安全需求
• 本地化，配套使用SM3

缺点：

• 主要在国内使用，国际化可能存在兼容性问题
• 实现复杂

实际应用

• 被广泛用于政府部门、金融机构和大型企业的信息系统中
• 电子政务、电子商务、可信计算等多个领域

总结

本文主要简单介绍了非对称加密算法 RSA、ECC 和 SM2 的基本原理，以及它们的实现过程。对比对称加密，非对称加密算法的最大优势就是保障了密钥分发的安全性、支持数字签名。

因此，现在大部分的认证和签名场景，其实使用的都是非对称加密算法。比如，在SSH登录、Git上传等场景中，我们都可以将自己的公钥上传到服务端，然后由客户端保存私钥。