Are you ready?
- 数据驱动文化优于最高-薪者的意见,但并不是所有的统计数据都是有指导价值的,比如用具有相关性的统计数据做决策可能是荒唐的,而基于随机分流的A/B测试获得的具有平均因果效应的统计数据是能用于决策的。
- 因果关系能辅助决策,A/B测试能体现因果关系,所以A/B测试能用于决策。
- A/B测试的核心思想是基于随机分流获取样本模拟整体流量,其中A是对照组,B是实验组,对比两个样本在不同策略下的表现。A/B测试的样本受随机分流的影响,无法完全等价于整体流量,因此需通过假设检验,验证样本表现差异是由于分流导致的影响,还是策略带来的影响。
1. 什么是A/B测试?
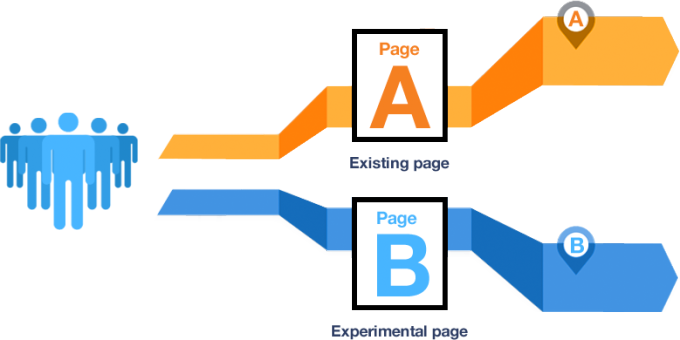
AB 实验是从线上流量中取出一小部分,完全随机地分给原策略 A(对照组)和新策略 B(实验组),两组策略中的用户特点类似。将原策略 A 和新策略 B 分别展示给对应的用户组,运行一段时间后,运用统计方法分析埋点上报的数据,得到新策略 B 带来的指标变化,并以此判断新策略 B 是否符合预期。
举个例子:2012年,必应(微软的搜索引擎)的一名员工提出了关于改进搜索页广告标题陈列方式的一个想法 :将标题下方的第一行文字移至标题同一行,以使标题变长,如下图所示。
一名研发者实现了该需求,并通过真实的用户反馈来评估它:随机给一部分用户显示新的标题陈列方式,而对另一部分用户依旧显示老版本。用户在网站上的行为,包括广告点击以及产生的营收都被一一记录。
该测试开始后的几个小时,“营收过高”的警报被触发,提示实验有异常。实验组,也就是新的标题陈列方式,产生了过高的广告营收。这种“好到难以置信”的警报非常有用,它们通常能提示严重的漏洞,如营收被重复上报(双重计费)或者因网页出错而导致只能看到广告。
然而就这个实验而言,营收增长是真实有效的。在没有显著损害其他关键用户体验指标的情况下,必应的营收增长高达12%,这意味着仅在美国,当年的营收增长就将超过1亿美金。这一实验在后来很长一段时间里被多次重复验证。
这就是一个A/B测试的例子:用于比较A和B两组变体的对照实验,A和B也分别称为对照组和实验组。
2. 为什么需要A/B测试?
2.1 建立数据驱动决策文化而不是依赖最高薪者的意见
首先是一个想法的价值很难被预估,即使是最高薪者也不一定有全局的判断力,需要靠数据驱动说话。
2.2 使用能正确驱动决策的数据
这里需要说明一点:相关性的数据不能用于决策,因果关系可以辅助决策,而A/B实验能提供因果关系;相关!=因果。
关于相关性,举个例子,人均巧克力消费量与诺贝尔奖比例关系图如下图所示。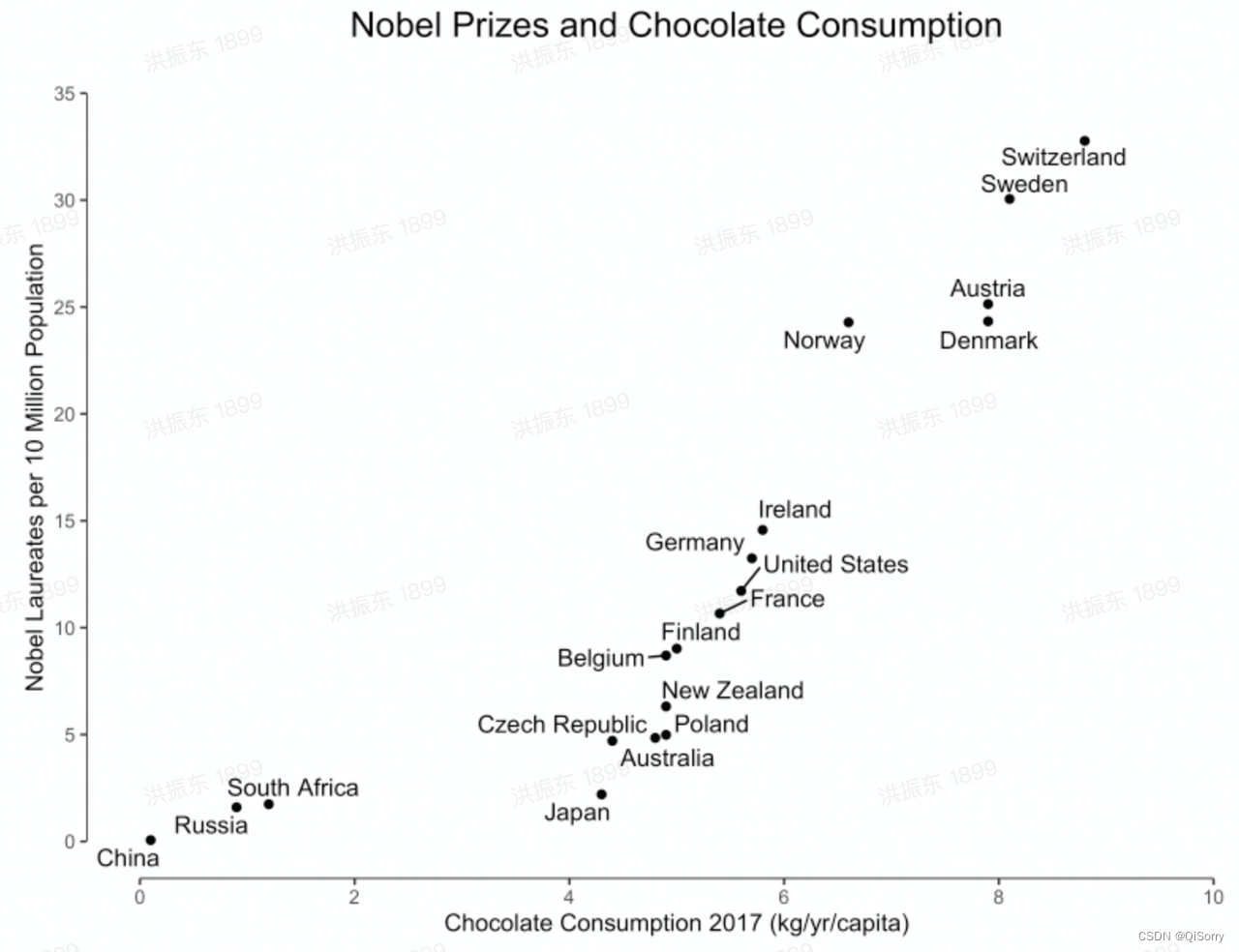
如可以看出二者之间存在相关性,那如果现在我想提升获取诺贝尔奖的人数,那我们总不能让这个国家的人都吃巧克力吧。虽然获得诺贝尔奖的人数和巧克力的消费类有相关关系,但他们二者并没有因果关系,而只有因果关系才能辅助决策。
因果关系试图回答的:其他不变,改变A后,Y的取值发生变化,则AY有因果关系。
我们可以构建两个组(实验组和对照组,每个组随机包含很多个体,保证这两个组的潜在结果是一致的),通过在实验组改变A值,观察Y值是否不同,从而确定AY的因果关系,这就是A/B测试。
以刚才微软改进搜索页广告标题陈列方式为例,A表示是否改进广告标题陈列方式,Y表示收入。那么就存在两个潜在结果,一个是改变之后的收入,另一个是不改变的收入,这两种结果之间的差异就体现了改进搜索页广告标题陈列方式和收入的因果关系,而这个差异就可以辅助决策。
AY(收入)对照组否10亿实验组是10.8亿
3. 分流
3.1 分流的重要性
首先先说一下分流服务的作用:
- 保证每个用户都是被随机分配到实验组或对照组,从而保证同一实验不同组的潜在结果一致,减少抽样误差对实验结果造成的影响;
- 分流服务帮助各实验层流量正交,保证两组用户的潜在结果一致;
- 分流服务保证实验分组的稳定。
关于流量正交不理解没关系,下面会详细说明。
为什么说分流服务非常重要呢?AB实验中,我们希望样本能够尽可能的随机,减少抽样误差对实验结果造成的影响。而我们的每一次实验,都要依靠分流服务帮助我们,从整体流量中抽取一部分,并进行分组。这就意味着,如果分流服务有问题,我们的实验结果就可能是不可靠的。
3.2 分流的相关术语
- 实验层:将有限流量复制无数次满足多实验的流量诉求,每次复制后的流量称为一个流量层,每一层都是100%的流量。需保证有相关性实验的流量开在同一层(举个例子,我想探究提交按钮的颜色对于用户的体验影响,那么实验遍历就是按钮颜色,如果我们想探究黄,蓝,绿三种颜色,那么我们就要开三个实验,那么这三个实验必须开在同一层)。
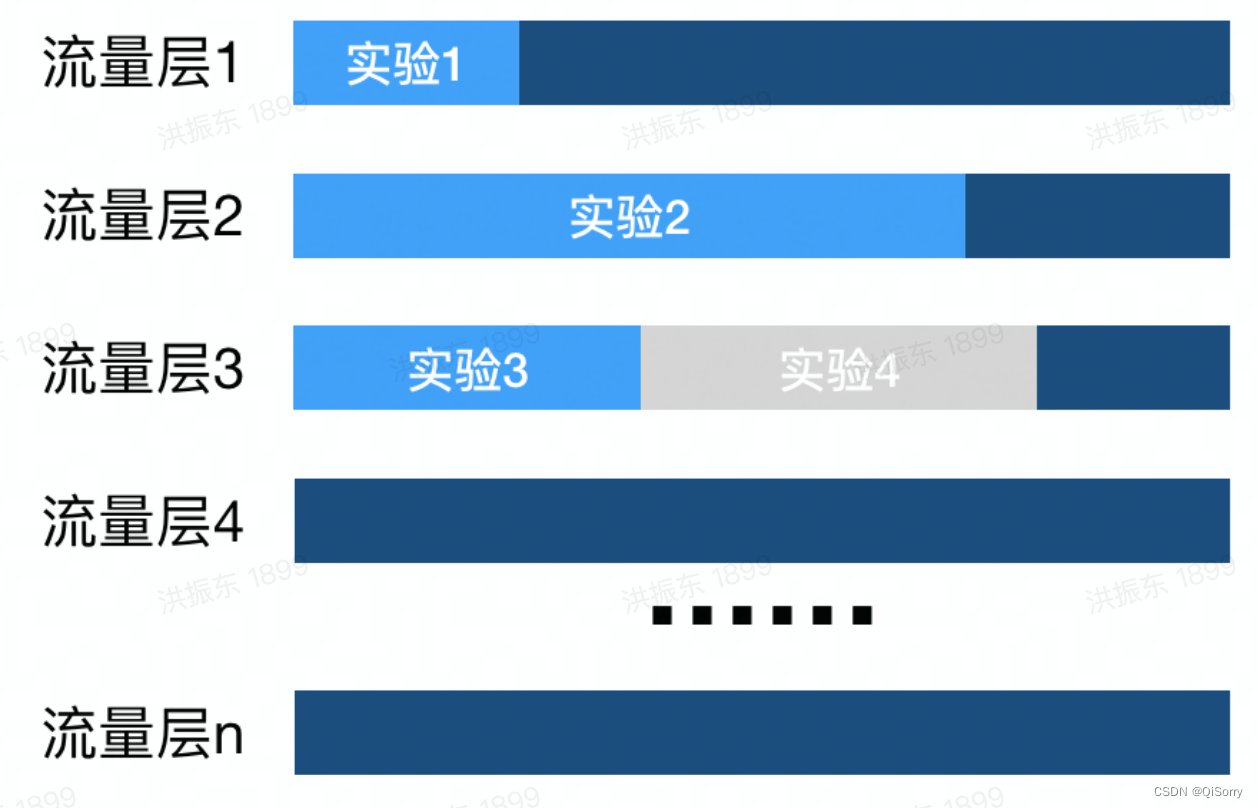
- 正交:每一个实验的实验组或对照组的用户,都均匀地分布在其他实验层的实验组和对照组中,避免实验相互影响。一个用户可能会命中多个实验。
3.3 如何保证流量正交
我们如何理解正交呢?
首先看一下在非正交的情况下:
假如有A和B两个实验分别在实验层1和实验层2,实验组分别为A1和B1,对照组分别为A2和B2,在流量未正交的情况下,实验组A1和实验组B1的用户是一样的,如果实验组B1的指标涨了,我们无法判断B1的策略是否是真的有效,因为这个也有可能是实验组A1的策略导致的。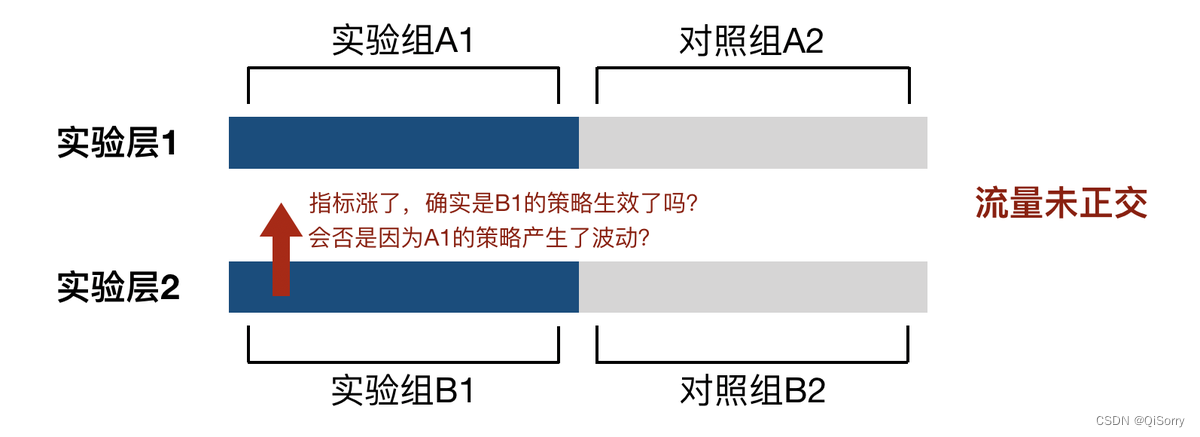
其次在正交的情况下:
正交情况下,实验组A1的用户被均匀分配到了实验B的实验组B1和对照组B2,在这种情况下,就算A1策略有影响,由于A1策略的用户被均匀分到了B1和B2,对B1和B2的影响效果也是一样的。如果实验组B1指标涨了,那就能够说明是B1的策略生效了。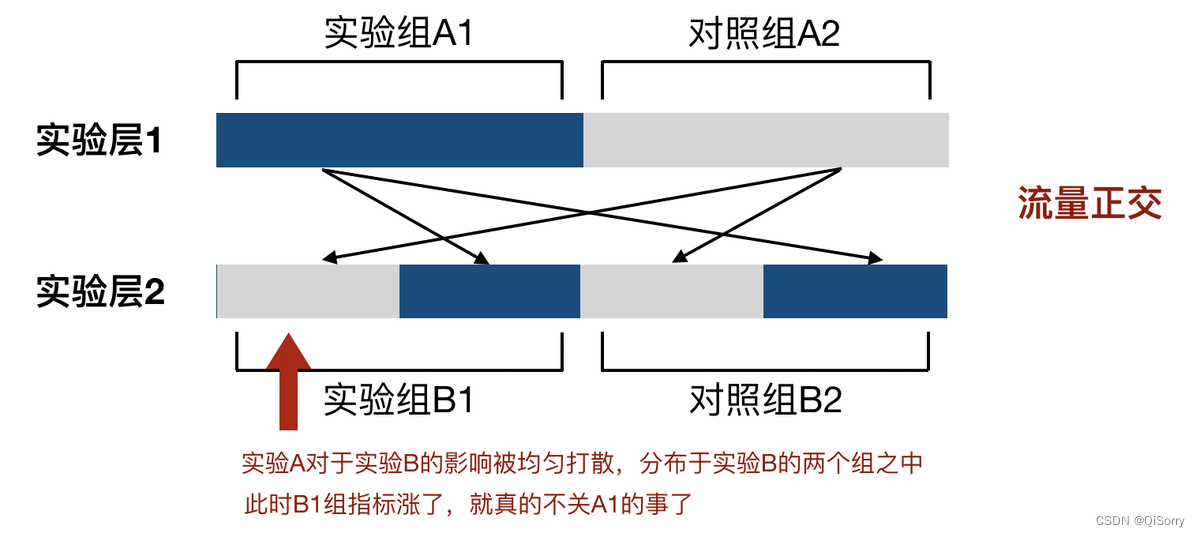
字节Libra平台的分流方案:2次hash
- 第一次hash:hash(uid, 流量层名称)%1000,判断用户进哪个桶
- 第二次hash:hash(uid, 实验名称)%2,判断用户进入实验组还是对照组
- 分流服务在分配流量时,会先把每一层的流量平均分配为1000份,每一份被称为一个“哈希桶”。用户在进入实验层的时候,分流服务会通过「哈希函数」和「取模运算」,将用户分配到某个桶里;
- 经过分流服务的处理,将所有用户都分配到桶里,那么这1000个桶里,每桶都有0.1%的流量。同一层上的不同实验在调用流量时,就会按照实验所需的流量的百分比,随机领取到不同数量的桶;
- 假设开设的实验调用3%的流量,那么就会领取到30个桶。
第一次hash保证了不同流量层上的实验所用的流量正交。是因为uid和流量层名称不一样,这样就可以保证不同流量层的用户被随机分配到了不同的桶中,也就保证了各实验层的之间的流量正交。
第二次hash保证实验分组的稳定。如果用户在多日实验中,用户来回被不同的组命中(用户看到的界面可能会不一样),一方面会影响用户的使用体验,另一方面,则会很大程度上影响实验指标的准确程度。因此,在实验中,不管用户打开产品多少次,我们都需要他被稳定地分入同一个组里(要么进入实验组,要么进入对照组),这也是分流服务必须要保证的。
在实验过程中,uid和实验名称是不变的,这就意味着同一实验下的同一不管什么时候进行第二次hash他们的结果都是一样的,也就是进入到的组是不变的。
4. 假设检验
分流的方案上尽可能地使两组用户的潜在结果一致,而且我们是从全部流量中抽取了一部分流量,如果对照组和实验组的指标存在差异,我们需要通过假设检验来判断这个差异是不是由抽样误差导致的?有多大概率是由抽样误差导致的?如果这个概率很小,我们是不是可以认为实验组和对照组指标出现的差异是由于策略不同导致的?
以抛硬币为例,随机抛一枚硬币多次,我们都知道每次出现正面的概率是50%,但下面的结果也是有可能发生的:
第 i 次抛硬币结果可能性1正50%2正25%3正12.5%4正6.25%5正≈3%
此时我们开始质疑这个硬币是否有问题,有以下两种可能:
- 是真硬币:观察到的最终结果出现的可能性大于某个值,我们认为这是枚真硬币
- 是假硬币:观察到的最终结果出现的可能性小于某个值,我们认为这是枚假硬币。
在硬币场景中,我们更能接受该硬币是枚假硬币,因为如果是一枚真硬币,连续出现5次正面的可能性为3%,这种可能性太小了,我们拒绝接受这是一枚真硬币。这里证明硬币真假使用的方法就是假设检验。
对应在 AB Test 中,实验组和对照组指标存在差异,我们也会质疑实验组策略到底有没有显著影响,这个差异是否由于抽样误差导致的,此时也有以下两种可能:
- 策略没有影响:观察的结果出现的可能性大于某个值,我们认为策略没有显著影响;
- 策略有影响:观察的结果出现的可能性小于某个值,我们认为策略有显著影响。
在 AB Test 中,我们也可以做同样的假设检验。首先构造一个原假设(实验组和对照组没有差异),在原假设成立的基础上计算观察到的现象出现的概率(p-value),概率越小,证明拒绝原假设的可能性就越大,差异就越显著。通常情况下,p-value < 5%时,认为差异是显著的,可以拒绝原假设。
AB Test 的核心统计学理论是(双样本)假设检验,里面涉及到很多统计知识。
第一类错误&显著性水平(α)
第二类错误( β )&统计功效
MDE
上面列出来的三个内容,本文并没有涉及,包括在大数据场景下,我们面对的用户实验数据量是TB甚至是PB级别的,这时候我们的显著性又如何计算?总不能用python/R来处理这些数据吧?这时候就要借助大数据组件如 Hive / Spark,分桶等方案来计算显著性,后面有机会也会在将这些知识分享给大家。
版权归原作者 QiSorry 所有, 如有侵权,请联系我们删除。