0
0

详解高级数据结构之 跳表

一、跳表的介绍

在学习跳表之前我们要知道什么是跳表？

其实，简单来说，跳表其实是一种多层的有序链表。跳表来源于链表，在链表的基础上结合了二分的思想进行改造，我们把改造之后的数据结构叫做跳表（Skip list）。

我们知道：二分查找针对的有序数组，时间复杂度是o(logn)。如果是有序链表，查询和插入的的时间复杂度是o(n)。跳表就是链表的“二分查找”。redis的有序集合用的就是跳表算法。

跳表的做法就是给链表做索引，而且是分层索引，第一层索引是n/2个，第二层的索引是n/4个，第三层索引是n/8个，即每隔两个数据就记下个索引，索引对象记录了三个数据，一个是要比对的数据值，一个是索引的下一个索引，还有就是索引下方对应的索引或链表。

跳表的第k级的索引个数是n/(2的k次方），计算跳表的时间复杂度过程：索引层数*索引每层查找个数，如果每隔2个数据做索引，那么每层查找个数就是3，假设索引层数为h，n/(2的h次方）= 2，即最上面索引一定是2个，得到h = logn - 1，即h = logn，而每层最多查找3次，所以总次数=h * 3，即3logn，去掉常量3，即为logn。

跳表是需要建立索引的，大概建立n个索引，是用空间换时间的典型算法，只不过跳表所需要的空间不是链表中存储的数据对象，它只需要上述中的3个值即可，真实场景中可能空间损耗很小的，相对于存储的数据对象而言。 建立索引可以每隔2个数据建立索引，也可以隔3个或5个，时间复杂度是5logn，空间复杂度是n/2了，如果n不大，差距并不大，但是可以灵活调整，毕竟隔的数大了，空间损耗小了，时间长了，即有效的平衡内存占用及查询效率。 跳表的动态插入和删除也会变得高效起来，也是logn，但是有个问题，动态插入数据后，数据个数发生变化，需要更新索引，如何更新索引是门学问，这里redis采用了随机函数办法，比如要插入数据6，那么通过随机函数生成需要动态建立索引的层数，比如4，这时从链表向索引上方数4层，每层都建立一个新的索引6即可。

二、跳表的数据结构图

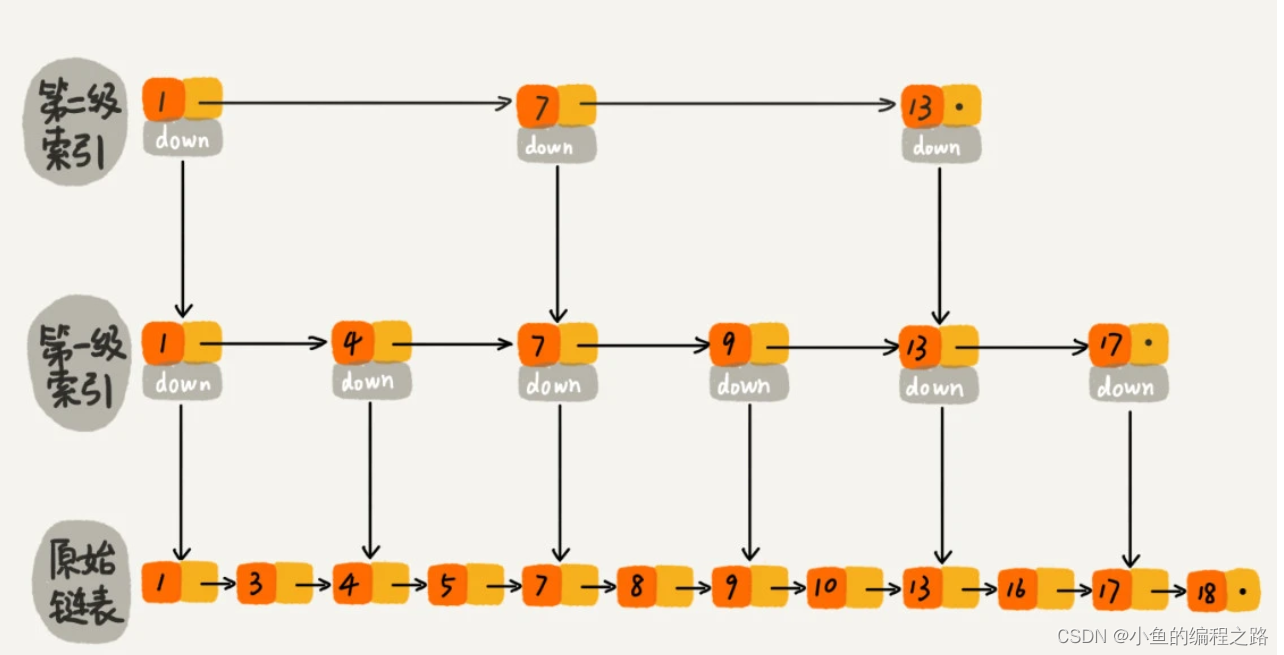
三、跳表的查找

算法的执行效率可以通过时间复杂度来度量，我们知道，在一个单链表中查询某个数据的时间复杂度是 O(n)。那在一个具有多级索引的跳表中，查询某个数据的时间复杂度是多少呢？

这个时间复杂度的分析方法比较难想到。我把问题分解一下，先来看这样一个问题，如果链表里有 n 个结点，会有多少级索引呢？

在跳表中，每两个结点会抽出一个结点作为上一级索引的结点，那第一级索引的结点个数大约就是 n/2，第二级索引的结点个数大约就是 n/4，第三级索引的结点个数大约就是 n/8，依次类推，也就是说，第 k 级索引的结点个数是第 k-1 级索引的结点个数的 1/2，那第 k级索引结点的个数就是 n/(2的k次方)。

假设索引有 h 级，最高级的索引有 2 个结点。通过上面的公式，我们可以得到 n/(2h)=2，从而求得 h=log2n-1。如果包含原始链表这一层，整个跳表的高度就是 log2n。我们在跳表中查询某个数据的时候，如果每一层都要遍历 m 个结点，那在跳表中查询一个数据的时间复杂度就是 O(m*logn)。

那m到底是多少呢，假设我们要查找的数据是 x，在第 k 级索引中，我们遍历到 y 结点之后，发现 x 大于 y，小于后面的结点 z，所以我们通过 y 的 down 指针，从第 k 级索引下降到第 k-1 级索引。在第 k-1 级索引中，y 和 z 之间只有 3 个结点（包含 y 和 z），所以，我们在 K-1 级索引中最多只需要遍历 3 个结点，依次类推，每一级索引都最多只需要遍历 3 个结点。

过上面的分析，我们得到 m=3，所以在跳表中查询任意数据的时间复杂度就是 O(logn)。这个查找的时间复杂度跟二分查找是一样的，这也体现了空间换时间的效率之高。

四、跳表是不是很浪费内存？

比起单纯的单链表，跳表需要存储多级索引，肯定要消耗更多的存储空间。那到底需要消耗多少额外的存储空间呢？我们来分析一下跳表的空间复杂度。

假设原始链表大小为 n，那第一级索引大约有 n/2 个结点，第二级索引大约有 n/4 个结点，以此类推，每上升一级就减少一半，直到剩下 2 个结点。如果我们把每层索引的结点数写出来，就是一个等比数列。

这几级索引的结点总和就是 n/2+n/4+n/8…+8+4+2=n-2。所以，跳表的空间复杂度是 O(n)。也就是说，如果将包含 n 个结点的单链表构造成跳表，我们需要额外再用接近 n 个结点的存储空间。

实际上，在软件开发中，我们不必太在意索引占用的额外空间。在讲数据结构和算法时，我们习惯性地把要处理的数据看成整数，但是在实际的软件开发中，原始链表中存储的有可能是很大的对象，而索引结点只需要存储关键值和几个指针，并不需要存储对象，所以当对象比索引结点大很多时，那索引占用的额外空间就可以忽略了。也就是说，当存储对象占用的内存很大时，指针占据的内存就可以忽略不计了。

五、跳表高效的动态插入和删除

跳表不仅支持查找操作，还支持动态的插入、删除操作，而且插入、删除操作的时间复杂度也是 O(logn)。

在单链表中，一旦定位好要插入的位置，插入结点的时间复杂度是很低的，就是 O(1)。但是，这里为了保证原始链表中数据的有序性，我们需要先找到要插入的位置，这个查找操作就会比较耗时。

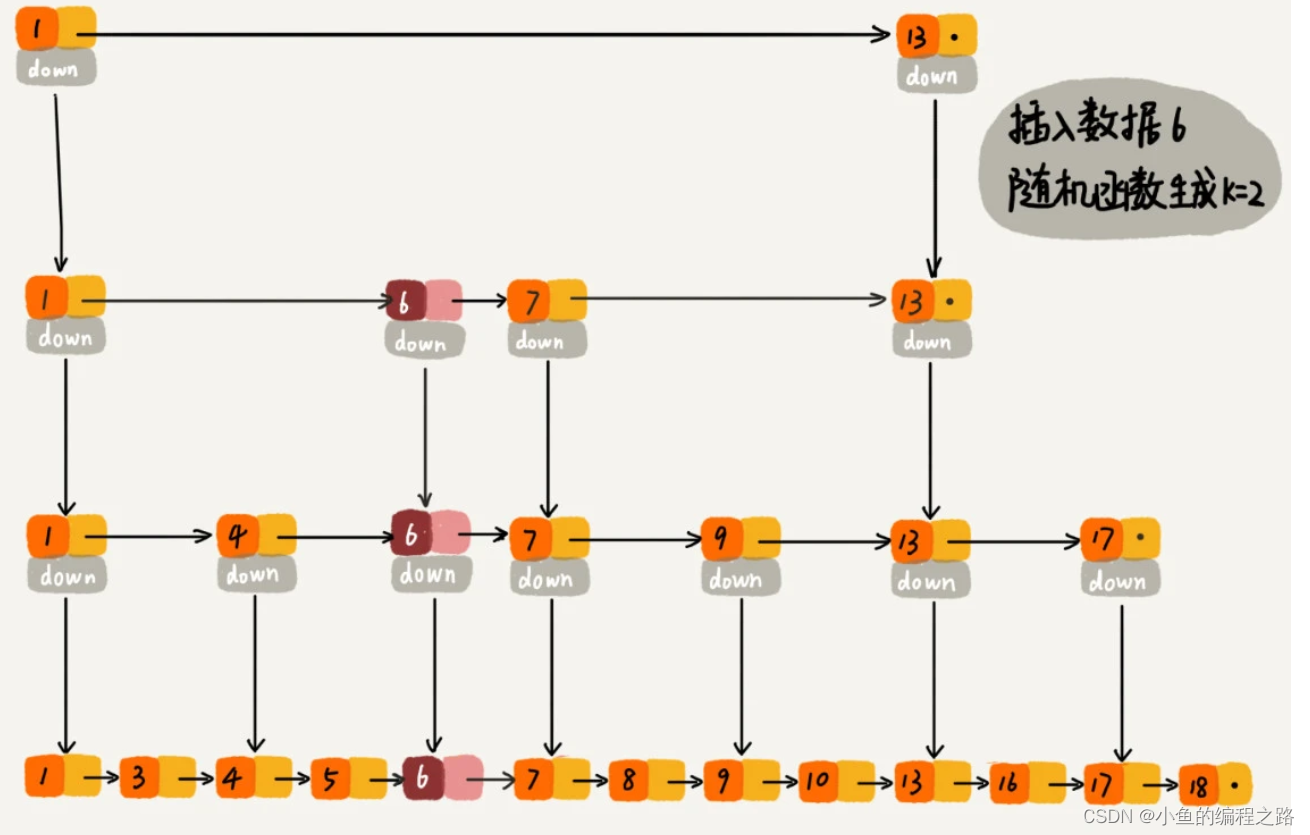
对于纯粹的单链表，需要遍历每个结点，来找到插入的位置。但是，对于跳表来说，我们讲过查找某个结点的时间复杂度是 O(logn)，所以这里查找某个数据应该插入的位置，方法也是类似的，时间复杂度也是 O(logn)。下面这张图中可以很清晰地看到插入的过程：

对于跳表的删除操作，如果这个结点在索引中也有出现，我们除了要删除原始链表中的结点，还要删除索引中的。因为单链表中的删除操作需要拿到要删除结点的前驱结点，然后通过指针操作完成删除。所以在查找要删除的结点的时候，一定要获取前驱结点。当然，如果我们用的是双向链表，就不需要考虑这个问题了。

跳表索引动态更新

当我们不停地往跳表中插入数据时，如果我们不更新索引，就有可能出现某 两个索引结点之间数据非常多的情况。极端情况下，跳表还会退化成单链表。

作为一种动态数据结构，我们需要某种手段来维护索引与原始链表大小之间的平衡，也就是说，如果链表中结点多了，索引结点就相应地增加一些，避免复杂度退化，以及查找、插入、删除操作性能下降。

** 跳表是通过随机函数来维护它的“平衡性”。**

当我们往跳表中插入数据的时候，我们可以选择同时将这个数据插入到部分索引层中。而我们通过一个随机函数，来决定将这个结点插入到哪几级索引中，比如随机函数生成了值 K，那我们就将这个结点添加到第一级到第 K 级这 K 级索引中。

六、跳表的特性

  1. 跳表的本质是一个多层的有序链表，同时结合了二分和链表的思想；
  2. 由很多层索引组成，每一层索引是通过随机函数随机产生的，每一层都是一个有序的链表，默认是升序 ；
  3. 最底层的链表包含所有元素；
  4. 如果一个元素出现在第i层的链表中，则它在第i层之下的链表也都会出现；
  5. 跳表的每个节点包含两个指针，一个指向同一链表中的下一个元素，一个指向下面一层的元素。

七、小结

跳表使用空间换时间的设计思路，通过构建多级索引来提高查询的效率，实现了基于链表的“二分查找”。跳表是一种动态数据结构，支持快速地插入、删除、查找操作，时间复杂度都是 O(logn)。

跳表的空间复杂度是 O(n)。不过，跳表的实现非常灵活，可以通过改变索引构建策略，有效平衡执行效率和内存消耗。

八、C++实现简易跳表

#include<iostream>
#include<ctime>
using namespace std;

const int MAXN_LEVEL=10;

struct SNode
{
    int key;
    SNode *forword[MAXN_LEVEL];
};

struct SkipList
{
    int nowLevel; 
    SNode *head;
};

/************************************************
*参数：myList为指向跳表头结点的指针
*功能:初始化跳表
*************************************************/
void InitSkipList(SkipList *& myList)
{
     myList=new SkipList;
     myList->nowLevel=0;
     myList->head=new SNode;
     for(int i=0;i<MAXN_LEVEL;i++)
         myList->head->forword[i]=NULL;
}

/************************************************
*参数：myList为指向跳表头结点的指针，x为待插入元素，countRet为查找次数
*功能:在跳表中插入元素x
*************************************************/
bool InsertSkipList(SkipList *myList,int val)
{
    if(NULL==myList)
        return false;
    int k=myList->nowLevel;
    SNode *q,*p=myList->head;
    SNode *upDateNode[MAXN_LEVEL];
    while(k>=0)
    {
        q=p->forword[k];
        while(NULL!=q&&q->key<val)
        {
            p=q;
            q=p->forword[k];
        }
        if(NULL!=q&&q->key==val)
             return false;
        upDateNode[k]=p;
        --k;
    }
    k=rand()%(MAXN_LEVEL-1);
    if(k>myList->nowLevel)
    {
        k=++myList->nowLevel;
        upDateNode[k]=myList->head;
    }
    p=new SNode;
    p->key=val;
    for(int i=0;i<=k;i++)
    {
        q=upDateNode[i];//q指向前面小于x的
        p->forword[i]=q->forword[i];
        q->forword[i]=p;
    }
    //for(int i=k+1;i<=myList->nowLevel;i++)
     for(int i=k+1;i<MAXN_LEVEL;i++)
            p->forword[i]=NULL;
    return true;
}

/************************************************
*参数：myList为指向跳表头结点的指针，x为待查找元素，countRet为查找次数
*功能:查找跳表中是否存在元素x
*************************************************/
SNode* FindSkipList(SkipList * myList,int val,int &countRet)
{
    if(NULL==myList)
        return NULL;

    int k=myList->nowLevel;
    SNode *q,*p=myList->head;
    while(k>=0)
    {
        q=p->forword[k];
        ++countRet;
        while(NULL!=q&&q->key<val)
        {
            ++countRet;
            p=q;
            q=p->forword[k];
        }
        if(NULL!=q&&q->key==val)
            return q;
        --k;
    }
    return NULL;
}

/************************************************
*参数：myList为指向跳表头结点的指针，x为待删除元素
*功能:删除跳表中元素x
*************************************************/
bool DeleteSkipList(SkipList * myList,int val)
{
    int tmpCountRet=0;
    SNode *ret=FindSkipList(myList,val,tmpCountRet);
    if(NULL==ret)
        return false;

    int k=myList->nowLevel;
    SNode *q,*p=myList->head;
    SNode *upDateNode[MAXN_LEVEL];

     for(int i=0;i<MAXN_LEVEL;i++)
        upDateNode[i]=NULL;
    
    while(k>=0)
    {
        q=p->forword[k];
        while(NULL!=q&&q->key<val)
        {
            p=q;
            q=p->forword[k];
        }
        if(NULL!=q&&q->key==val)
             upDateNode[k]=p;
        --k;
    }

    for(int i=0;i<=myList->nowLevel;i++)
    {
        q=upDateNode[i];//q指向前面小于x
        if(NULL!=q&&q->forword[i]==ret)
            q->forword[i]=ret->forword[i];
    }
    delete ret;
    return true;
}

int main()
{
    int val;
    SkipList *  myList;
    InitSkipList(myList);

    while(cin>>val)
    {
        if(!InsertSkipList(myList,val))
            cout<<val<<"插入失败!"<<endl;
        else cout<<val<<"插入成功!"<<endl;
        
        int countRet=0;
        if(NULL!=FindSkipList(myList,val,countRet))
            cout<<val<<"查找成功!"<<endl;
        else cout<<val<<"查找失败!"<<endl;
        cout<<"共查找了"<<countRet<<"次"<<endl;
        
        DeleteSkipList(myList,val);
        countRet=0;
        if(NULL!=FindSkipList(myList,val,countRet))
            cout<<val<<"查找成功!"<<endl;
        else cout<<val<<"查找失败!"<<endl;
        cout<<"共查找了"<<countRet<<"次"<<endl;
        

    }
    system("Pause");
}
标签： 数据结构 c++
本文转载自: https://blog.csdn.net/weixin_52967653/article/details/125941153
版权归原作者 小鱼的编程之路 所有， 如有侵权，请联系我们删除。
登录后发布评论

“详解高级数据结构之 跳表”的评论:

还没有评论
关于作者
...
overfit同步小助手
文章同步
相关阅读

java+vue计算机毕设茶叶产品质量安全可追溯系统【源码+程序+论文+开题】

Postman：Postman API测试：Postman数据驱动测试实践

解决：IntelliJ IDEA 项目中代码文件不能运行的问题(即：J 标文件的问题)

Docker：安装 MongoDB 的详细指南

Git - 两种方式撤销已提交到远端仓库的记录并删除提交记录

Kafka 原理

Flink Memory Management原理与代码实例讲解

文章导航