60题学会动态规划系列：动态规划算法第五讲

子数组系列题目

文章目录

• 1.最大子数组和
• 2.环形子数组的最大和
• 3.乘积最大数组
• 4.乘积为正数的最长子数组长度
• 5.等差数列划分
• 6.最长湍流子数组
• 7.单词拆分
• 8.环绕字符串中唯一的子字符串

---

1.最⼤⼦数组和

力扣链接：力扣

给你一个整数数组

nums

，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

**子数组 **是数组中的一个连续部分。

这道题是子数组问题中的经典问题，同时也非常简单，题目告诉子数组可以是一个元素，在这里要注意子数组和子序列的区别（子数组是连续的，子序列可以连续可以不连续，子序列包含了子数组）

1.状态表示

根据经验我们就以常用的以某一个位置为结尾来定义状态表示，如果可以推出状态转移方程，那么我们的状态表示就是没有问题的，如果推不出来状态转移方程，那么就需要重新状态表示。

dp[i]表示以i位置为结尾的连续子数组的最大和

2.状态转移方程

我们要求状态转移方程，首先要看如何求i位置的最大和，这里其实只有两种情况1.我们的i位置的数比前面的所有子数组的最大和加上我们i位置的数都要大，那么i位置的最大和就是nums[i]。如果i位置前面的所有连续子数组的最大和加上i位置的值是小于前面的所有连续子数组的最大和的，那么i位置的最大和就是前面的所有连续子数组的最大和。我们的状态表示是以i位置为结尾的连续子数组的最大和，那么i位置前面的i-1不就是前面的所有子数组的最大和吗，所以状态转移方程为：

dp[i] = max(dp[i-1]+nums[i],nums[i])

3.初始化

从状态转移方程中我们可以看到只有第一个位置会越界，所以我们初始化dp[0]即可，一个元素的最大和就是这个元素本身，所以dp[0] = nums[0]

4.填表

从左向右

5.返回值

我们dp表中存放的是从0~n-1每一个位置为结尾的连续子数组的最大和，所以返回的是表中最大的值。

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
       int n = nums.size();
       vector<int> dp(n,0);
       dp[0] = nums[0];
       int ret = dp[0];
       for (int i = 1;i<n;i++)
       {
           dp[i] = max(dp[i-1]+nums[i],nums[i]);
           ret = max(dp[i],ret);
       }
       return ret;
    }
};

2.环形子数组的最大和

力扣链接：力扣

给定一个长度为

n

的环形整数数组

nums

，返回*

nums

的非空 子数组 的最大可能和 *。

环形数组* *意味着数组的末端将会与开头相连呈环状。形式上，

nums[i]

的下一个元素是

nums[(i + 1) % n]

，

nums[i]

的前一个元素是

nums[(i - 1 + n) % n]

。

子数组 最多只能包含固定缓冲区

nums

中的每个元素一次。形式上，对于子数组

nums[i], nums[i + 1], ..., nums[j]

，不存在

i <= k1, k2 <= j

其中

k1 % n == k2 % n

。

对于环形的问题，我们的解决办法一般都是将环形问题转换成普通子数组问题，下面我们分析一下：

1.状态表示

首先我们还是根据经验将状态表示为：dp[i]表示以i位置为结尾的子数组最大和，这个时候我们发现这一个状态表示无法解决下面这种情况：

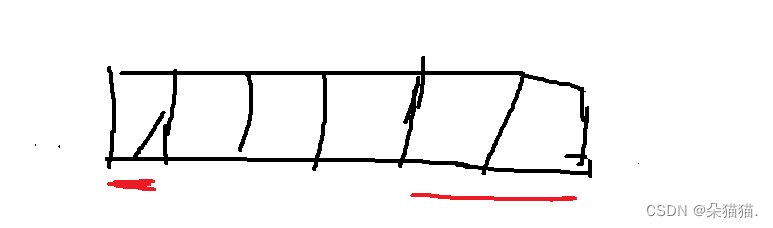
红色划线部分就是环形区域，对于在环形区域的最大和我们无法用第一个状态表示求出，那么如何将这个环形问题转化为普通问题呢？其实我们只需要求出中间这部分区域的子数组的最小和：

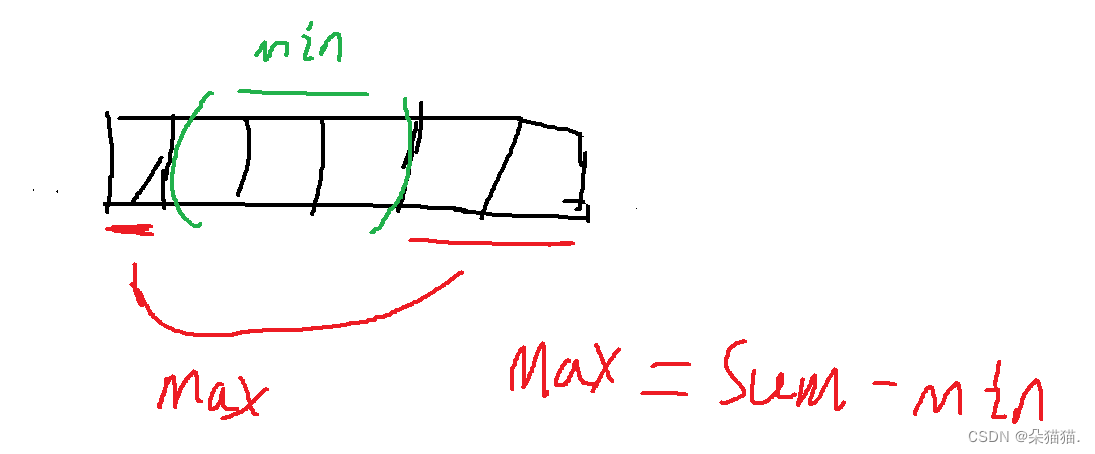
因为我们每次求出的都是一段连续的子数组，所以当我们求出从0~n-1位置以其中任何位置为结尾的子数组的最小值，那么一旦最大值是在环形区域，我们只需要让整个数组的和减去最小值那么就得到了环形区域的最大和。

f[i]表示以i位置为结尾的子数组最大和。

g[i]表示以i位置为结尾的子数组的最小和。

2.状态转移方程

f[i] = max(f[i-1] + nums[i],nums[i])

g[i] = min(g[i-1]+nums[i],nums[i])

3.初始化

通过状态转移方程我们可以看到只有第一个位置会越界，所以只初始化第一个位置。

f[0] = nums[0],g[0] = nums[0]

4.填表

从左向右，两个表一起填

5.返回值

返回f表中最大值和sum-g表中最小值的最大值：

return max(fmax,sum-gmin),但是这里还有一个小细节：

如果数组中全是负数的话，那么我们求出的子数组中的最小和就是整个数组的和，这种情况下最大值只有f表中存在，如果像上面那样就会发现sum-gmin==0,0肯定比fmax大就返回0了，实际上我们要返回的是数组中的最大值，0不是数组中的值所以不能返回，所以正确的返回是：

return sum==gmin?fmax:max(fmax,sum-gmin)

class Solution {
public:
    int maxSubarraySumCircular(vector<int>& nums) {
       int n = nums.size();
       if (n==1) return nums[0];
       vector<int> f(n,0),g(n,0);
       f[0] = nums[0];
       g[0] = nums[0];
       int fmax = INT_MIN;
       int gmin = INT_MAX;
       int sum = nums[0];
       for (int i = 1;i<n;i++)
       {
           f[i] = max(f[i-1]+nums[i],nums[i]);
           fmax = max(f[i],fmax);
           g[i] = min(g[i-1]+nums[i],nums[i]);
           gmin = min(g[i],gmin);
           sum+=nums[i];
       }
       return sum==gmin?fmax:max(fmax,sum-gmin);
    }
};

当我们运行起来发现当数组只有一个元素的时候是跑不过的，因为只有一个元素的时候不会进入for循环，直接就return了，但是这个时候fmax还是整形最小值,gmin还是整形最大值，max()中做判断的时候sum-gmin就会发生整形溢出，所以只有一个元素的时候我们直接返回这个元素即可。

3.乘积最⼤⼦数组

力扣链接：力扣

给你一个整数数组

nums

，请你找出数组中乘积最大的非空连续子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。

测试用例的答案是一个 32-位 整数。

子数组 是数组的连续子序列。

1.状态表示

我们假如以前面的经验以dp[i]表示以i位置为结尾的子数组的最大乘积的话，代码写出来与上一题并没有多少差别，但是允许的时候只能过一般测试用例，这是因为数中有负数的存在，负数与最小的负数相乘就是一个大的正数，这一点用一个状态是解决不了的，所以：

f[i]表示i位置为结尾的子数组的最大乘积

g[i]表示i位置为结尾的子数组的最小乘积

2.状态转移方程

我们以i位置划分，发现i位置有三种状态，n[i]大于0或者n[i]小于0或者n[i]等于0，对于等于0的状态，乘任何数还是0，所以可以先不用考虑，当n[i]大于0时，最大值有可能是n[i]*f[i-1]也有可能是n[i]，最小值有可能是n[i]*g[i-1]也有可能是n[i]。

所以：当n[i]>0,f[i] = max(f[i-1]*n[i],n[i]) , g[i] = min(g[i-1]*n[i],n[i])

对于n[i]<0的情况，与上面的相反：

当n[i]<0,f[i] = max(n[i]*g[i-1],n[i]) , g[i] = min(f[i-1]*n[i],n[i])

3.初始化

第一个位置会越界，所以初始化两个表第一个位置：

f[0] = g[0] = nums[0]

4.填表

两个表一起填，从左向右。

5.返回值

返回f表中的最大值

class Solution {
public:
    int maxProduct(vector<int>& nums) {
        int n = nums.size();
        if (n==1) return nums[0];
        vector<int> f(n,0),g(n,0);
        f[0] = g[0] = nums[0];
        int ret = f[0];
        for (int i = 1;i<n;i++)
        {
            if (nums[i]>0)
            {
                f[i] = max(nums[i]*f[i-1],nums[i]);
                g[i] = min(g[i-1]*nums[i],nums[i]);
            }
            else if(nums[i]<0)
            {
                f[i] = max(nums[i]*g[i-1],nums[i]);
                g[i] = min(f[i-1]*nums[i],nums[i]);
            }
            ret = max(ret,f[i]);
        }
        return ret;
    }
};

当我们初始化第1一个位置时会出现两个问题，一个数的时候无法进入for循环，所以需要提前处理一个数的情况。当nums[0]是f表中最大值时，我们发现如果让ret是整形最小值时是不能通过程序的，所以我们可以将ret初始化为f[0]。

当然我们上面的写法实际上优点繁琐，下面我们用开虚拟节点的方式简化一下代码：

class Solution {
public:
    int maxProduct(vector<int>& nums) {
        int n = nums.size();
        vector<int> f(n+1,0),g(n+1,0);
        f[0] = g[0] = 1;
        int ret = INT_MIN;
        for (int i = 1;i<=n;i++)
        {
            f[i] = max(nums[i-1],max(f[i-1]*nums[i-1],g[i-1]*nums[i-1]));
            g[i] = min(nums[i-1],min(g[i-1]*nums[i-1],f[i-1]*nums[i-1]));
            ret = max(ret,f[i]);
        }
        return ret;
    }
};

我们优化了两点：

1.通过加虚拟节点可以解决第一次的代码中只有一个元素和nums[0]就是最大值的情况

2.我们不用考虑n[i]大于0还是小于0，直接一股脑都做判断找出最大值即可。

4.乘积为正数的最长子数组长度

力扣链接：力扣

给你一个整数数组

nums

，请你求出乘积为正数的最长子数组的长度。

一个数组的子数组是由原数组中零个或者更多个连续数字组成的数组。

请你返回乘积为正数的最长子数组长度。

根据上一题的经验，要求正数我们一种状态肯定是不可以的，要考虑负负得正的情况就必须有两种状态。

1.状态表示

f[i]表示以i位置为结尾乘积为正数的最长子数组长度

g[i]表示以i位置为结尾乘积为负数的最长子数组长度

2.状态转移方程

我们可以将i位置分为3种状态，等于0，大于0，小于0.要注意的是：不管是g表还是f表如果n[i]等于0那么长度一定为0，因为0（0乘任何数都为0）既不是正数也不是负数.当n[i]大于0时，只需要找到i位置前面的乘积为正数的最长子数组然后加上本身长度1即可，即使f[i-1]=0，由于n[i]大于0自己本身也是1所以f[i] = f[i-1]+1.对于g[i]，如果n[i]大于0那么要找负数的最长长度的话前面必须是负数，所以g[i-1]+1，但是如果g[i-1]为0 的话，就说明i前面没有乘积为负数的最长子数组，而又因为自己本身是大于0的，我们的g表要的负数，所以当g[i-1]等于0时，g[i]=0.

对于n[i]小于0的情况，那么找到i前面的乘积为负数的子数组然后相乘就变成了正数，所以f[i] = g[i-1]+1,但是g[i-1]有可能为0，一旦为0说明i前面没有乘积为负数的子数组，又因为n[i]是小于0的，所以当g[i-1]等于0时，f[i]只能为0.g[i]中如果n[i]小于0，那么只要找到i前面的乘积为正数的子数组（负数乘正数还是负数）然后加上自身的长度，即使f[i-1]等于0，但是n[i]本身小于0长度为1，所以不用特殊判断f[i-1]是否为0.

3.初始化

我们采用开虚拟节点的方式，第一个元素的时候需要dp[i-1]的值，从状态转移方程来看，为了不影响后续填表，将两个虚拟位置初始化为0即可。

4.填表

从左向右两个表一起填

5.返回值

由于f表中存放的是多个子数组的结果，所以需要遍历找到f表中最大值。

class Solution {
public:
    int getMaxLen(vector<int>& nums) {
       int n = nums.size();
       vector<int> f(n+1,0),g(n+1,0);
       int ret = 0;
       for (int i = 1;i<=n;i++)
       {
           if (nums[i-1]>0)
           {
               f[i] = f[i-1]+1;
               g[i] = g[i-1]==0?0:g[i-1]+1;
           }
           else if(nums[i-1]<0)
           {
               f[i] = g[i-1]==0?0:g[i-1]+1;
               g[i] = f[i-1]+1;
           }
           ret = max(ret,f[i]);
       }
       return ret;
    }
};

5.等差数列划分

力扣链接：力扣

如果一个数列 至少有三个元素 ，并且任意两个相邻元素之差相同，则称该数列为等差数列。

• 例如，[1,3,5,7,9]、[7,7,7,7] 和 [3,-1,-5,-9] 都是等差数列。

给你一个整数数组

nums

，返回数组

nums

中所有为等差数组的 子数组 个数。

子数组 是数组中的一个连续序列。

这道题中题目给的有用信息有：必须是一个等差数组，每个等差数组至少3个元素。

1.状态表示

根据经验我们以dp[i]表示以i位置为结尾的等差数组的子数组的个数。

2.状态转移方程

当以i位置为结尾时，要想是一个等差数列，满足的条件必须是n[i]-n[i-1] = n[i-1]-n[i-2],只有满足了这个条件，说明i位置元素可以和前面的等差数列匹配，这个时候dp[i] = dp[i-1] + 1.

如果不满足刚刚等差数列的条件，那么以i位置为结尾是没有等差数列的，所以dp[i] = 0

3.初始化

通过状态转移方程我们可以看到0,1这两个位置会越界，所以我们直接初始化这两个位置，由于等差数组必须有3个元素，刚开始的两个元素无法组成等差数组，所以dp[0]和dp[1]都是0

4.填表

从左向右

5.返回值

我们题目要求的是返回所有等差数组的个数，而我们dp[i]计算的是i位置为结尾的等差数组的个数，所以我们应该将dp表中每个位置的等差数组的个数相加最后返回。

class Solution {
public:
    int numberOfArithmeticSlices(vector<int>& nums) {
        int n = nums.size();
        vector<int> dp(n,0);
        int sum = 0;
        for (int i = 2;i<n;i++)
        {
            if (nums[i]-nums[i-1]==nums[i-1]-nums[i-2])
            {
                dp[i] = dp[i-1]+1;
            }
            else 
            {
                dp[i] = 0;
            }
            sum+=dp[i];
        }
        return sum;
    }
};

注意：我们填dp表的时候一定是从第3个位置也就是下标为2的位置开始填，因为前两个元素是无法构成等差数组的。

6.最长湍流子数组

力扣链接：力扣

给定一个整数数组

arr

，返回

arr

的 最大湍流子数组的长度** **。

如果比较符号在子数组中的每个相邻元素对之间翻转，则该子数组是 湍流子数组 。

更正式地来说，当

arr

的子数组

A[i], A[i+1], ..., A[j]

满足仅满足下列条件时，我们称其为湍流子数组：

• 若 i <= k < j ： - 当 k 为奇数时， A[k] > A[k+1]，且- 当 k 为偶数时，A[k] < A[k+1]；
• **或 **若 i <= k < j ： - 当 k 为偶数时，A[k] > A[k+1] ，且- 当 k 为奇数时， A[k] < A[k+1]。

这道题我们不用看题目描述，因为说的有些繁琐了，我们直接看测试用例，通过测试用例我们发现湍流子数组实际上就是下图这样的：

上图中曲线的上升或者下降其实就是两个数的差是正还是负，只要满足正负正负或者负正负正就是湍流子数组，并且通过题目描述我们得知，相等情况并不属于湍流，但是一个元素的时候也属于湍流。

1.状态表示

如果以dp[i]表示以i位置为结尾的最长湍流子数组的话，我们发现运行后的测试用例的结果每次都会少，这是因为i位置的状态其实是有两种状态的，如果是湍流子数组，那么i-1到i位置有可能是上升状态，也有可能是下降状态，所以我们有两个状态表示：

f[i]表示以i位置为结尾并且呈上升状态的最长湍流子数组

g[i]表示以i位置为结尾并且呈下降状态的最长湍流子数组

2.状态转移方程

既然i位置有两种状态，下面我们就分析一下：

当n[i]>n[i-1]，说明到i位置是上升状态，这个时候要组成湍流子数组那么i-1前面就必须是下降状态，所以f[i] = g[i-1]+1。当n[i]>n[i-1]时，我们的g[i]存放的结尾是下降状态，这个时候条件不满足，但是我们说过一个元素也算湍流子数组，并且一个元素的时候既可以代表上升也可以代表下降状态，所以g[i] = 1.

当n[i]<n[i-1]，说明到i位置是下降状态，这个时候要组成湍流子数组那么i-1前面就必须是上升状态，所以g[i] = f[i-1]+1。当n[i]<n[i-1]时，我们的f[i]存放的结尾是上升状态，这个时候条件不满足，但是我们说过一个元素也算湍流子数组，并且一个元素的时候既可以代表上升也可以代表下降状态，所以f[i] = 1.

3.初始化

由于一个元素也属于湍流子数组，所以我们将两个表都初始化为1，这样遇到dp[i]为1的情况我们就不用考虑了。

4.填表

从左向右两个表一起填

5.返回值

返回g表和f表中的最大值

class Solution {
public:
    int maxTurbulenceSize(vector<int>& arr) {
        int n = arr.size();
        vector<int> f(n,1),g(n,1);
        int ret = f[0];
        for (int i = 1;i<n;i++)
        {
            if (arr[i]>arr[i-1])
            {
                f[i] = g[i-1]+1;
            }
            else if(arr[i]<arr[i-1])
            {
                g[i] = f[i-1]+1;
            }
            ret = max(f[i],max(g[i],ret));
        }
        return ret;
    }
};

让ret为f[0]的时候可以解决只有一个元素无法进入for循环的情况。

7.单词拆分

力扣链接：力扣

给你一个字符串

s

和一个字符串列表

wordDict

作为字典。请你判断是否可以利用字典中出现的单词拼接出

s

。

注意：不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。

这道题让我们用字典中的字符拼接字符串，下面我们就分析一下：

1.状态表示

我们就以经常用的dp[i]来表示：

dp[i]表示从0~i这个区间的字符串能否被拼接

2.状态转移方程

我们要验证以i为结尾的字符串是否可以被凭借，那么就需要找到以i为结尾的单词的首部，比如说leetcode中以d为结尾的时候我们枚举>=d的任何一个字符发现都没有在字典中找到对应的单词，那么就说明dp[i]为false，那么什么情况下是找到的呢？当我们以t为结尾，在找以t为结尾的字符串时发现首部为L的字符到t是一个完成的字符串leet，这个时候还没有结束，我们还需要判断首部前面的单词是否可以在字典中找到。

如上图，当以e结尾时，我们除了要判断以e结尾的单词是否能够找到，同时还要判断j前面的单词是否可以找到，但是我们的状态表示的是以某个位置为结尾的字符串能否被拼接，所以j前面的单词的状态就可以表示为dp[j-1](因为j是i结尾的首单词，所以j前面的状态是dp[j-1]

dp[i] = 如果dp[j-1]为真并且substr(j,i-j+1)这个单词能被找到，那么dp[i] = true

3.初始化

这里我们用虚拟节点的方式，不用虚拟节点初始化会麻烦很多，这里已经试过了。采用虚拟节点首先虚拟节点不能影响后续填表，所以dp[0] = true,可以看我们的状态转移方程，如果第一个虚拟节点为false,那么即使dp[i]实际为true，但是由于dp[j-1]为false，导致无法正确判断。

我们加了虚拟节点后，那么dp表就应该从1位置（初始化了0位置）开始填，但是字符串中的第一个字符实际下标是0，所以为了和实际的字符串下标匹配，我们在字符串前面加个空格，这样字符串的第一个字符的下标就是1了，与我们的dp表匹配。

4.填表

从左向右

5.返回值

题目要求整个字符串是否可以被拼接，所以我们应该是以最后一个字符为结尾的结果，所以返回dp[n]（因为虚拟节点所以可以访问n位置）

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
         int n = s.size();
         vector<bool> dp(n+1,false);
         dp[0] = true;
         unordered_set<string> hash;
         for (auto& s:wordDict) hash.insert(s);
         s = ' '+s;
         for (int i = 1;i<=n;i++)
         {
             for (int j = 1;j<=i;j++)
             {
                 if (dp[j-1]&&hash.count(s.substr(j,i-j+1)))
                 {
                     dp[i] = true;
                 }
             }
         }
         return dp[n];
    }
};

可以看到我们为了优化每次查找字符串是否在字典中的效率，我们将字典中的单词直接映射到了哈希表中。

8.环绕字符串中唯一的子字符串

力扣链接：力扣

定义字符串

base

为一个

"abcdefghijklmnopqrstuvwxyz"

无限环绕的字符串，所以

base

看起来是这样的：

• "...zabcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyzabcd....".

给你一个字符串

s

，请你统计并返回

s

中有多少 不同****非空子串 也在

base

中出现。

通过测试用例我们可以发现，这道题让我们求的实际上是连续的子字符串，比如实例3中，z,a,b三个单个的字符都可以在Base中找到，然后再看连续的子字符串，za是一个,ab是一个，zab也是一个，因为是环绕的z的后面就是a，所以zab也可以。

1.状态表示

dp[i]表示以i字符为结尾的子字符串的个数

2.状态转移方程

我们发现i位置如果能和前面匹配那么就会多一种方法，那么匹配的条件是什么呢？实际上就是s[i-1]+1==s[i]或者s[i-1]=='z'&&s[i]=='a'的时候符合条件，这个时候dp[i] = dp[i-1]+1

3.初始化

首先能越界的只有dp[0]，并且s[0]一定可以在base中找到，所以dp[0] = 1

因为题目给的字符串一定是小写字母组成，所以这一个字符一定属于26个字母中的任意一个，所以我们将dp表全部初始化为1，如果不满足转移方程的条件那么默认的1刚好合适。

4.填表

从左向右依次填表

5.返回值

我们要求的是s中所有在base中出现的子字符串，而我们dp[i]只是某一个位置的结果，所以我们应该加上dp表中所有的值才是正确答案。

当我们提交代码后发现很多测试用例都跑不过，这个时候我们发现我们的dp表是有重复结果的，如下图：

同样以c字符为结尾，我们保存两个结果，就比如下面这个例子更清晰：

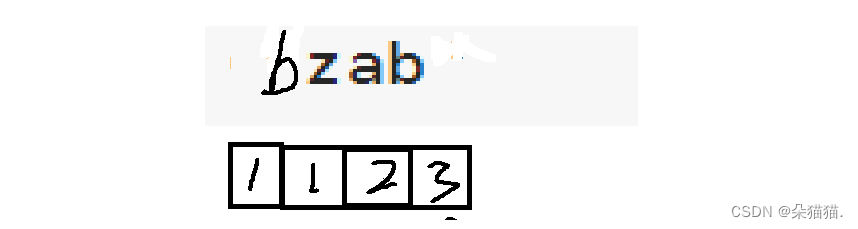比如这个字符串的结果应该是6，但是我们全部加起来是7，因为b自己本身多算了一次，所以我们需要对相同字符结尾的字符串去重，比如：ab和zab的结果我们只保留最大的那一个，因为最大的那个一定包含了之前的任何一个例子。我们去重的思想也很简单，开一个26大小的数组，每一个字符的结尾只会在数组中映射一遍，比如b 和 ab只能映射到hash[b-a]这个位置，而这个位置我们保存的是以b结尾的子字符串的最大值。

class Solution {
public:
    int findSubstringInWraproundString(string s) {
        int n = s.size();
        vector<int> dp(n,1);
        int sum = 0;
        for (int i = 1;i<n;i++)
        {
            if (s[i-1]+1==s[i] || s[i-1]=='z'&&s[i]=='a')
            {
                dp[i] = dp[i-1]+1;
            }
        }
        //去重dp表中相同的字符结尾的最小值，只保留最大值
        int hash[26] = {0};
        for (int i = 0;i<n;i++)
        {
            hash[s[i]-'a'] = max(hash[s[i]-'a'],dp[i]);
        }
        for (auto& e : hash) sum+=e;
        return sum;
    } 
};

这道题最抽象的部分在于去重，如果有不理解的可以将图画出来。