SVM Summary
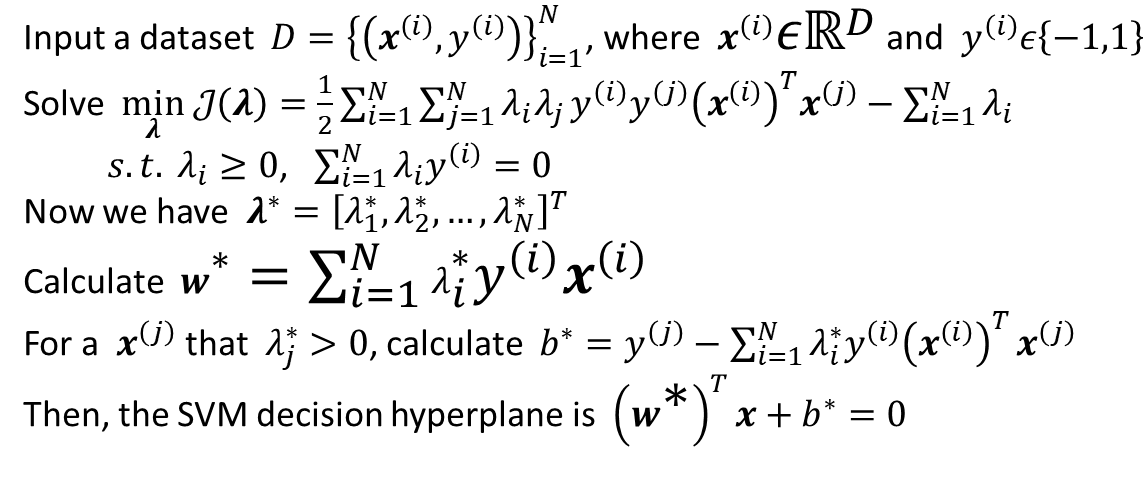
Example
Suppose the dataset contains two positive samples
x
(
1
)
=
[
1
,
1
]
T
x^{(1)}=[1,1]^T
x(1)=[1,1]T and
x
(
2
)
=
[
2
,
2
]
T
x^{(2)}=[2,2]^T
x(2)=[2,2]T, and two negative samples
x
(
3
)
=
[
0
,
0
]
T
x^{(3)}=[0,0]^T
x(3)=[0,0]T and
x
(
4
)
=
[
−
1
,
0
]
T
x^{(4)}=[-1,0]^T
x(4)=[−1,0]T. Please calculate the SVM decision hyperplane.
Calculate
min
λ
J
(
λ
)
=
1
2
∑
i
=
1
N
∑
j
=
1
N
λ
i
λ
j
y
(
i
)
y
(
j
)
(
x
(
i
)
)
T
x
(
j
)
−
∑
i
=
1
N
λ
i
\min_\lambda\ {\mathcal{J}(\lambda)} = \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N \lambda_i\lambda_jy^{(i)}y^{(j)}(x^{(i)})^Tx^{(j)} - \sum_{i=1}^N\lambda_i
λmin J(λ)=21i=1∑Nj=1∑Nλiλjy(i)y(j)(x(i))Tx(j)−i=1∑Nλi
s
.
t
.
λ
i
⩾
0
,
∑
i
=
1
N
λ
i
y
(
i
)
=
0
s.t. \ \ \ \ \ \ \ \ \lambda_i \geqslant 0,\ \ \ \ \ \ \sum_{i=1}^N\lambda_iy^{(i)}=0
s.t. λi⩾0, i=1∑Nλiy(i)=0
由
D
a
t
a
s
e
t
D
:
{
x
:
{
[
1
,
1
]
,
[
2
,
2
]
,
[
0
,
0
]
,
[
−
1
,
0
]
}
,
y
:
{
1
,
1
,
−
1
,
−
1
}
}
Dataset\ D:\{x:\{[1,1],[2,2],[0,0],[-1,0]\},y:\{1,1,-1,-1\}\}
Dataset D:{x:{[1,1],[2,2],[0,0],[−1,0]},y:{1,1,−1,−1}}可得下式:
min
λ
J
(
λ
)
=
1
2
(
2
λ
1
2
+
8
λ
2
2
+
λ
4
2
+
8
λ
1
λ
2
+
2
λ
1
λ
4
+
4
λ
2
λ
4
)
−
λ
1
−
λ
2
−
λ
3
−
λ
4
s
.
t
λ
1
⩾
0
,
λ
2
⩾
0
,
λ
3
⩾
0
,
λ
4
⩾
0
λ
1
+
λ
2
−
λ
3
−
λ
4
=
0
\min_\lambda\ {\mathcal{J}(\lambda)} = \frac{1}{2}(2\lambda_1^2+8\lambda_2^2+\lambda_4^2+8\lambda_1\lambda_2+2\lambda_1\lambda_4+4\lambda_2\lambda_4) \\- \lambda_1-\lambda_2-\lambda_3-\lambda_4\\ s.t \ \ \ \ \ \ \ \lambda_1 \geqslant 0,\lambda_2\geqslant 0,\lambda_3\geqslant 0,\lambda_4\geqslant 0\\ \lambda_1+\lambda_2-\lambda_3-\lambda_4 = 0
λmin J(λ)=21(2λ12+8λ22+λ42+8λ1λ2+2λ1λ4+4λ2λ4)−λ1−λ2−λ3−λ4s.t λ1⩾0,λ2⩾0,λ3⩾0,λ4⩾0λ1+λ2−λ3−λ4=0
since
λ
1
+
λ
2
=
λ
3
+
λ
4
→
λ
3
=
λ
1
+
λ
2
−
λ
4
\lambda_1+\lambda_2 = \lambda_3+\lambda_4 \to \lambda_3 = \lambda_1+\lambda_2 - \lambda_4
λ1+λ2=λ3+λ4→λ3=λ1+λ2−λ4:
min
λ
J
(
λ
)
=
λ
1
2
+
4
λ
2
2
+
1
2
λ
4
2
+
4
λ
1
λ
2
+
λ
1
λ
4
+
2
λ
2
λ
4
−
2
λ
1
−
2
λ
2
s
.
t
λ
1
⩾
0
,
λ
2
⩾
0
⟹
求
偏
导
{
∂
J
∂
λ
1
=
2
λ
1
+
4
λ
2
+
λ
4
−
2
=
0
∂
J
∂
λ
2
=
4
λ
1
+
8
λ
2
+
2
λ
4
−
2
=
0
∂
J
∂
λ
4
=
λ
1
+
2
λ
2
+
λ
4
=
0
\min_\lambda\ {\mathcal{J}(\lambda)} = \lambda_1^2+4\lambda_2^2+\frac{1}{2}\lambda_4^2+4\lambda_1\lambda_2+\lambda_1\lambda_4+2\lambda_2\lambda_4 - 2\lambda_1-2\lambda_2\\ s.t \ \ \ \ \ \ \ \lambda_1 \geqslant 0,\lambda_2\geqslant 0 \\ \\ \Longrightarrow ^{求偏导}\\ \left\{\begin{matrix} \frac{\partial \mathcal{J}}{\partial \lambda_1} = 2\lambda_1 +4\lambda_2+\lambda_4-2=0 \\ \frac{\partial \mathcal{J}}{\partial \lambda_2} = 4\lambda_1 +8\lambda_2+2\lambda_4-2=0 \\ \frac{\partial \mathcal{J}}{\partial \lambda_4} = \lambda_1 +2\lambda_2+\lambda_4=0 \end{matrix}\right.
λmin J(λ)=λ12+4λ22+21λ42+4λ1λ2+λ1λ4+2λ2λ4−2λ1−2λ2s.t λ1⩾0,λ2⩾0⟹求偏导⎩⎨⎧∂λ1∂J=2λ1+4λ2+λ4−2=0∂λ2∂J=4λ1+8λ2+2λ4−2=0∂λ4∂J=λ1+2λ2+λ4=0
Lagrange无解,所以极小值在边界上:
- 令 λ 1 = 0 , λ 3 = λ 1 + λ 2 − λ 4 \lambda_1 = 0, \lambda_3 = \lambda_1+\lambda_2 - \lambda_4 λ1=0,λ3=λ1+λ2−λ4带入 J ( λ ) \mathcal{J}(\lambda) J(λ)中,得: J ( λ ) = 4 λ 2 2 + 1 2 λ 4 2 + + 2 λ 2 λ 4 − 2 λ 2 ⟹ 求 偏 导 { ∂ J ∂ λ 2 = 8 λ 2 + 2 λ 4 − 2 = 0 ∂ J ∂ λ 4 = 2 λ 2 + λ 4 = 0 ⟹ { λ 2 = 1 2 λ 4 = − 1 ( ≤ 0 不 满 足 s . t . ) 再 令 : λ 2 = 0 , 则 λ 4 = 0 , J ( λ ) = 0 ; 或 λ 4 = 0 , 则 λ 2 = 1 4 , J ( λ ) = − 1 4 ; \mathcal{J}(\lambda) = 4\lambda_2^2+\frac{1}{2}\lambda_4^2++2\lambda_2\lambda_4 -2\lambda_2 \ \ \Longrightarrow ^{求偏导}\ \left{\begin{matrix} \frac{\partial \mathcal{J}}{\partial \lambda_2} = 8\lambda_2+2\lambda_4-2=0 \ \frac{\partial \mathcal{J}}{\partial \lambda_4} = 2\lambda_2+\lambda_4=0 \end{matrix}\right. \Longrightarrow \left{\begin{matrix} \lambda_2=\frac{1}{2} \ \lambda_4=-1(\le0 \ \ \ \ 不满足s.t.) \end{matrix}\right.\ 再令:\ \lambda_2 = 0,则\lambda_4=0, \mathcal{J}(\lambda) = 0;\ 或\lambda_4 = 0,则\lambda_2=\frac{1}{4}, \mathcal{J}(\lambda) = -\frac{1}{4}; J(λ)=4λ22+21λ42++2λ2λ4−2λ2⟹求偏导{∂λ2∂J=8λ2+2λ4−2=0∂λ4∂J=2λ2+λ4=0⟹{λ2=21λ4=−1(≤0 不满足s.t.)再令:λ2=0,则λ4=0,J(λ)=0;或λ4=0,则λ2=41,J(λ)=−41;
同理可得:
λ 2 = 0 \lambda_2 = 0 λ2=0 λ 1 = 0 , 则 λ 4 = 0 , J ( λ ) = 0 ; 或 λ 4 = 0 , 则 λ 1 = 1 , J ( λ ) = − 1 ; \lambda_1 = 0,则\lambda_4=0, \mathcal{J}(\lambda) = 0;\\ 或\lambda_4 = 0,则\lambda_1=1, \mathcal{J}(\lambda) =-1; λ1=0,则λ4=0,J(λ)=0;或λ4=0,则λ1=1,J(λ)=−1;λ 3 = 0 \lambda_3 = 0 λ3=0 λ 1 = 0 , 则 λ 2 = 2 13 , J ( λ ) = − 2 13 ; 或 λ 2 = 0 , 则 λ 1 = 2 5 , J ( λ ) = − 2 5 ; \lambda_1 = 0,则\lambda_2=\frac{2}{13}, \mathcal{J}(\lambda) = -\frac{2}{13};\\ 或\lambda_2 = 0,则\lambda_1=\frac{2}{5}, \mathcal{J}(\lambda) =-\frac{2}{5}; λ1=0,则λ2=132,J(λ)=−132;或λ2=0,则λ1=52,J(λ)=−52;λ 4 = 0 \lambda_4 = 0 λ4=0 λ 1 = 0 , 则 λ 2 = 1 4 , J ( λ ) = − 1 4 ; 或 λ 2 = 0 , 则 λ 1 = 1 , J ( λ ) = − 1 ; \lambda_1 = 0,则\lambda_2=\frac{1}{4}, \mathcal{J}(\lambda) = -\frac{1}{4};\\ 或\lambda_2 = 0,则\lambda_1=1, \mathcal{J}(\lambda) =-1; λ1=0,则λ2=41,J(λ)=−41;或λ2=0,则λ1=1,J(λ)=−1; 综上: λ 1 , 2 , 3 , 4 = { 1 , 0 , 1 , 0 } \lambda_{1,2,3,4} =\{1,0,1,0\} λ1,2,3,4={1,0,1,0} { W = ∑ i = 1 N λ i y ( i ) x ( i ) b = y ( j ) − ∑ i = 1 N λ i y ( i ) ( x ( i ) ) T x ( j ) ⟹ { W = [ 1 , 1 ] T b = − 1 ⟹ x ( 1 ) + x ( 2 ) − 1 = 0 \left\{\begin{matrix} W=\sum_{i=1}^{N} \lambda_{i} y^{(i)} \boldsymbol{x}^{(i)}\\ b=y^{(j)}-\sum_{i=1}^{N} \lambda_{i} y^{(i)}\left(x^{(i)}\right)^{T} x^{(j)} \end{matrix}\right. \Longrightarrow \left\{\begin{matrix} W = [1,1]^T\\ b=-1 \end{matrix}\right. \\\Longrightarrow x^{(1)}+x^{(2)} -1 =0 {W=∑i=1Nλiy(i)x(i)b=y(j)−∑i=1Nλiy(i)(x(i))Tx(j)⟹{W=[1,1]Tb=−1⟹x(1)+x(2)−1=0
本文转载自: https://blog.csdn.net/pylittlebrat/article/details/127830682
版权归原作者 ACxz 所有, 如有侵权,请联系我们删除。
版权归原作者 ACxz 所有, 如有侵权,请联系我们删除。