考试时允许使用草稿纸，请提前准备纸笔。考试过程中允许上厕所等短暂离开，但请控制离开时间

笔试得分60%一般通过，面试答对80%才能通过

合集：2023年最全前端面试题考点HTML5+CSS3+JS+Vue3+React18+八股文+手写+项目+笔试_参宿7的博客-CSDN博客

选择题总集合={前端，计算机基础（数据库，操作系统，数据结构与算法，计算机网络），行测}；

编程题总集合={常规算法（到具体情景），js手写，Dom操作}

例如：

• 美团：前端，计算机基础，行测，常规算法（前端：计算机基础=1:1）
• 小红书：前端，计算机基础，常规算法（前端：计算机基础=3：1）
• SHINE：前端，js手写
• 携程，京东：是先行测
• 百度：前端，计算机基础，常规算法，Dom操作

选择题

⭐是常考考点，其他是作为理解原理的补充，原理部分在大厂笔面试中会考到

常用设计模式

原则

• S – Single Responsibility Principle 单一职责原则- 一个程序只做好一件事- 如果功能过于复杂就拆分开，每个部分保持独立- 例如：Promise每个then中的逻辑只做好一件事
• O – OpenClosed Principle 开放/封闭原则- 对扩展开放，对修改封闭- 增加需求时，扩展新代码，而非修改已有代码- 例如：Promise如果新增需求，扩展then
• L – Liskov Substitution Principle 里氏替换原则 - 子类能覆盖父类- 父类能出现的地方子类就能出现
• I – Interface Segregation Principle 接口隔离原则 - 保持接口的单一独立- 类似单一职责原则，这里更关注接口
• D – Dependency Inversion Principle 依赖倒转原则 - 面向接口编程，依赖于抽象而不依赖于具体- 使用方只关注接口而不关注具体类的实现

//checkType('165226226326','mobile')
//result：false
let checkType=function(str, type) {
    switch (type) {
        case 'email':
            return /^[\w-]+(\.[\w-]+)*@[\w-]+(\.[\w-]+)+$/.test(str)
        case 'mobile':
            return /^1[3|4|5|7|8][0-9]{9}$/.test(str);
        case 'tel':
            return /^(0\d{2,3}-\d{7,8})(-\d{1,4})?$/.test(str);
        default:
            return true;
    }
}

想添加其他规则就得在函数里面增加 case 。违反了开放-封闭原则（对扩展开放，对修改关闭）

给 API 增加一个扩展的接口:

let checkType=(function(){
    let rules={
        email(str){
            return /^[\w-]+(\.[\w-]+)*@[\w-]+(\.[\w-]+)+$/.test(str);
        },
        mobile(str){
            return /^1[3|4|5|7|8][0-9]{9}$/.test(str);
        }
    };
    //暴露接口
    return {
        //校验
        check(str, type){
            return rules[type]?rules[type](str):false;
        },
        //添加规则
        addRule(type,fn){
            rules[type]=fn;
        }
    }
})();

//调用方式
//使用mobile校验规则
console.log(checkType.check('188170239','mobile'));
//添加金额校验规则
checkType.addRule('money',function (str) {
    return /^[0-9]+(.[0-9]{2})?$/.test(str)
});
//使用金额校验规则
console.log(checkType.check('18.36','money'));

创建型

单例模式

一个类只有一个实例，并提供一个访问它的全局访问点。

class LoginForm {
    constructor() {
        this.state = 'hide'
    }
    show() {
        if (this.state === 'show') {
            alert('已经显示')
            return
        }
        this.state = 'show'
        console.log('登录框显示成功')
    }
    hide() {
        if (this.state === 'hide') {
            alert('已经隐藏')
            return
        }
        this.state = 'hide'
        console.log('登录框隐藏成功')
    }
 }

 LoginForm.getInstance = (function () {
     let instance
     return function () {
        if (!instance) {
            instance = new LoginForm()
        }
        return instance
     }
 })()

let obj1 = LoginForm.getInstance()
obj1.show()

let obj2 = LoginForm.getInstance()
obj2.hide()

console.log(obj1 === obj2)

优点：只会实例化一次。简化了代码的调试和维护

缺点：有可能导致模块间的强耦合 从而不利于单元测试。

应用：登录框

工厂模式

工厂模式定义一个用于创建对象的接口，这个接口由子类决定实例化哪一个类。

该模式使一个类的实例化延迟到了子类。

而子类可以重写接口方法以便创建的时候指定自己的对象类型。

class Product {
    constructor(name) {
        this.name = name
    }
    init() {
        console.log('init')
    }
    fun() {
        console.log('fun')
    }
}

class Factory {//创建对象的接口
    create(name) {
        return new Product(name)
    }
}

// use
let factory = new Factory()
let p = factory.create('p1')
p.init()
p.fun()

优点：有利于消除对象间的耦合，提供更大的灵活性

缺点：添加新产品时，需要编写新的具体产品类,一定程度上增加了系统的复杂度

抽象工厂模式

结构型

代理模式

装饰器模式

行为型

责任链模式

观察者模式

const p1 = new Promise((resolve, reject) => {
    setTimeout(() => {
        resolve('result')
    },
    1000);
}) 

p1.then(res => console.log(res), err => console.log(err))

分析Promise的调用流程：

• Promise的构造方法接收一个executor()，在new Promise()时就立刻执行这个executor回调
• executor()内部的异步任务被放入宏/微任务队列，等待执行
• then()被执行，收集成功/失败回调，放入成功/失败队列
• executor()的异步任务被执行，触发resolve/reject，从成功/失败队列中取出回调依次执行

观察者模式：

收集依赖 -> 触发通知 -> 取出依赖执行

在Promise里，执行顺序是

then收集依赖 -> 异步触发resolve -> resolve执行依赖

。

class MyPromise {
  // 构造方法接收一个回调
  constructor(executor) {
    this._resolveQueue = []    // then收集的执行成功的回调队列
    this._rejectQueue = []     // then收集的执行失败的回调队列

    /*由于resolve/reject是在executor内部被调用, 
    因此需要使用箭头函数固定this指向, 否则找不到this._resolveQueue*/

    let _resolve = (val) => {
      // 从成功队列里取出回调依次执行
      while(this._resolveQueue.length) {
        const callback = this._resolveQueue.shift()
        callback(val)
      }
    }
    // 实现同resolve
    let _reject = (val) => {
      while(this._rejectQueue.length) {
        const callback = this._rejectQueue.shift()
        callback(val)
      }
    }
    // new Promise()时立即执行executor,并传入resolve和reject
    executor(_resolve, _reject)
  }

  // then方法,接收一个成功的回调和一个失败的回调，并push进对应队列
  then(resolveFn, rejectFn) {
    this._resolveQueue.push(resolveFn)
    this._rejectQueue.push(rejectFn)
  }
}

操作系统

进程

程序、进程、线程⭐

程序：（静态）以 文件形式 存于 硬盘

进程：（传统OS）资源分配 和 独立调度 的 基本单位，进程 实体 的 运行过程

线程：（引入线程的OS）独立调度 的 基本单位

进程 的状态 和 转换

1. 运行

2. 就绪：仅缺处理机

3. 阻塞/等待：等待资源（除处理机）可用 或 输入/输出完成

4. 创建：正创建；

5. 结束：正消失；

         <--****时间片/优先级****--
   

新建---创建--->就绪---调度--->运行----退出--->终止

             事件发生↖****阻塞****↙等待事件

死锁

⭐常考类型：进程Pi各需资源S Xi个，则Smin/Nmax不死锁条件：S=∑(Xi-1)+1

1. 定义：多进程 ∵资源竞争 而造成 相互等待 的僵局，无外力作用下 都无法 继续推进
2. 原因：非剥夺资源的 竞争 + 进程的 非法推进顺序（含 信号量 使用不当）
3. 充要：

等待循环+Pi的资源 必须 由 Pi+1 满足（当各类资源＝1，则循环等待＝死锁）

1. 必要条件：b->a、c->d

2. 互斥访问

3. 非剥夺资源

4. 请求****和保持

5. 循环等待

处理

预防

避免

检测

分配

严格，

宁愿闲置资源

折中，

运行时判断是否可能死锁

宽松，并发性最强

只要允许 就分配

操作

破坏必要条件之一：

一次请求all；剥夺；按资源序分配

算法通过 是否安全状态，找 可能的安全序列

定期检查 是否死锁

优点

适用突发处理，不必剥夺

不必剥夺，限制条件弱，系统性能较好

不延长进程初始化时间，

允许 对死锁 现场处理

缺点

效率低，进程初始化时间长；饥饿

剥夺次数过多；不便灵活申请资源

需知 将来需求资源；

可能 长时阻塞进程

剥夺解除死锁，造成损失

1. 预防：

破坏必要条件：

1. 互斥访问：某些场合 必须保证 互斥，∴实现 可能性小：
2. 非剥夺资源：释放已获得，造成前段工作失效；反复申请+释放，增加开销，降低吞吐

（常用于 易于保存和恢复的资源，eg：CPU的寄存器+内存资源；而非打印机etc）

1. 请求和保持：预先静态分配（一次申请完）；饥饿
2. 循环等待：资源编号，只能按****递增申请，同类资源一次申请完

（需编号稳定，限制了设备增加；可能 用资源和规定顺序不同，造成浪费资源；编程麻烦）

1. 避免：（死锁****=>不安全状态**** ）

银行家算法：Max，Need，Allocation，Available

1. 检测：

2. 死锁定理：S状态的 资源分配图 不可完全简化

3. 解除：

4. 剥夺（暂停）：挂起 某些进程，并抢夺资源（应防止 被挂起的进程 长期得不到资源）

5. 撤销（关闭）：（按 进程 优先级+撤销代价）撤销 部分甚至全部 进程，并抢夺资源

6. 回退（回放）：一/多个进程 回退到 足以避免死锁，自愿****释放资源（要求 系统 保持进程 的历史信息，设置还原点）

并发和并行

并发：逻辑上的同时发生（simultaneous）一个处理器同时处理多个任务。
并行：物理上的同时发生，是指多个处理器或者是多核的处理器同时处理多个不同的任务。

处理机调度

调度层次

多道批处理系统 大多有作业调度，其他系统则不需要

1. 低级/作业调度：外/辅存 后备--->入内存，建进程，分资源，获 竞争处理机权利
2. 中级/内存调度：暂不能运行--->外存 挂起（提高内存利用率+系统吞吐量）
3. 高级/进程调度：按某种方法/策略 分配

调度基本准则

1. CPU利用率
2. 系统吞吐量：单位时间内 CPU完成的作业量
3. 周转时间＝作业完成时间－提交时间＝t总；
4. 带权周转时间＝
5. 等待时间＝∑等待处理机时间；（判断 效率）
6. 响应时间＝首次响应时刻－提交时刻；

调度方式

1. 非剥夺/抢占式：适用 多数 批处理系统
2. 剥夺/抢占式：提高 系统吞吐率+响应率

调度算法⭐

（含作业/进程）

平均等待时间：时间片轮转 较长（上下文切换 费时）； 短作业优先 最短

FCFS

短作业优先

高响应比

RR

多级反馈队列

抢占

x

√

√

√

对内算法?

非抢占

√

√（默认）

√（默认）

x

对内算法?

适用

无

批处理OS

无

分时

通用

1. FCFS先来先服务（First Come First Serve）：利于长作业，CPU繁忙型****作业
2. SJF短作业优先：一个/若干 估计运行时间 最短 作业 入内存
3. SPF短进程优先：一个最短 进程 调度，分配处理机
4. 优先级：静优先级 取决 进程类型（系统>用户），要求资源（I/O>计算），用户要求

动态priority＝nice+k1cpuTime-k2waitTime（k1，k2>0调整所占比例）

• 高响应比 优先（主要 作业）＝FCFS+SJF；无 饥饿

t总/t实＝响应比Rp＝

1. 时间片轮转RR（主要 分时）：长短 取决 系统响应时间，就绪进程数，系统处理能力

2. 多级反馈队列＝时间片+优先级：

3. 特点：

• 级↓的就绪队列，优先级↑，时间片↑
• 新进程入内存，先1级，时间片用完则降级；第n级队列 时间片轮转
• i级队列空，才执行i+1级队列
• 若执行j级队列时，k级队列入进程（k<j），则抢占，当前进程回j队列末尾

1. 优势：

• 终端型作业用户：短作业优先（大多交互型，常短小）
• 短批处理作业用户：周转时间短
• 长批处理作业用户：经过前几个队列的部分执行，不会长时间无响应

内存管理

内存空间的扩充：从逻辑上扩充，虚拟存储/自动覆盖技术

• *源程序->可在内存中* 执行的程序：

1. 编译：编译程序 编译 源代码 成 若干个 目标模块
2. 链接：链接程序 链接 目标模块 + 所需****库函数，形成 一个 完整 的装入模块****（形成逻辑地址）
3. 装入：装入程序 将 装入模块 装入 内存（形成绝对地址）

• 相对/逻辑地址：编译后，每个目标模块 都从0号单元开始编址
• 逻辑地址空间：各个目标模块 的 相对地址 构成 的统一 从0号单元开始编址的 集合
• （内存管理的具体机制 完全透明，只有系统编程人员 才涉及，用户程序/程序员只需 知道逻辑地址）
• 物理地址空间：内存 中 物理单元的集合
• 地址重定位：逻辑地址->物理地址

连续空间分配策略算法⭐

分配策略算法

首次适应FF

最佳适应BF

最坏适应WF

邻近适用NF

空闲分区链接

地址递增

容量递增

容量递减

循环 首次适应

性能

最简单、快、好

****最多 ****外部碎片

很快没大内存块

内存末尾**** 碎片****

比较

（∵留下了 高地址的大空闲区，∴更可能满足进程）

优于顺序：FF 可能>BF >WF，FF 通常>NF

页面置换算法⭐

• ****最佳(OPT)****置换算法：替换 最长时间内/永久 不再被访问
• ∵最低缺页率，不可实现，∴只拿来评价其他算法
• *先进先出(FIFO)置换算法（队列*）：Belady异常（分配物理块数↑，页故障数↑）
• 最近最久*未使用(LRU)置换算法（堆栈*）：性能接近OPT，但需寄存器+栈；困难，开销大
• 理论可证明，堆栈类算法 不可能出现 Belady异常
• 时钟(CLOCK)/最近未使用(NRU) 置换算法：循环扫描 缓冲区
• 简单CLOCK 算法：

使用位：每一帧关联一个附加位/访问位

使用位 置1：首次装入/再被访问

候选帧 集合：看做 循环缓冲区，有一个指针与之关联

替换：按装入顺序扫描/上次扫描位置，扫描查找到0的帧，之前的1帧置0

• 改进型CLOCK算法：+ 修改位m（修改过的页，被替换前，需写回外存）

替换 第一个帧（u****＝0，m＝0）

重新扫描，替换 第一个帧（u＝0，m＝1），跳过的帧u置0

指针回到 最初位置，所有帧 u置0，重复①

数据结构

链表

1. 指针：是结点的相对地址，即数组下标，即游标
2. 分配：预先 分配 连续 的 内存空间
3. 结束标志：next=-1

a

-->

b

-->

c

^

下标

data

next

0

2

1

b

4

2

a

1

3

4

c

-1

栈

压栈 的 出入序列

（以 ****入栈 ****1 2 3 4 5 为例）

（1）出栈p首时，p前的序列A，只能逆序出栈，且插在A中每个元素后面

eg：4****； 4_3_2_1_

（2）p出栈序列的前一个元素p1，可能为p的前面的 或 后一个结点

eg：出栈 p1,3 则p1可能=1,2;4

n个不同元素进栈，出栈序列数

合法的出栈序列的数量=出栈序列的总数-非法序列的数量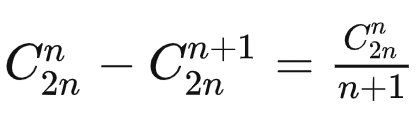

卡特兰数Catalan

栈指针

操作

初始S.top=-1，即top指向栈顶

S.top=0

共享栈，top指向栈顶

栈顶元素

S.data[S.top]

S.data[S.top-1]

S.data[S.top]

进栈

S.data[++top]=x;

S.data[top++]=x;

S.data[--top1]=x;

出栈

x=S.data[top--];

x=S.data[--top];

x=S.data[top1++];

栈空

S.top==-1;

S.top=0;

top1==MaxSize; top0=0;

栈满

S.top==MaxSize-1;

S.top==MaxSize;

top1-top0=1;

1. 缺点：数组上界 约束 入栈，对 最大空间 估计不足时，可能上溢（整个 存储空间满时）
2. 共享栈：栈顶向 共享空间 延伸，栈底 在两端，优点：更有效 利用 存储空间

表达式求值

将表达式构建成中序二叉树，然后先序求值

前，中，后缀 指 op在 两 操作数 中的位置

1. 中缀表达式：A+Bx（C-D）-E/F依赖 运算符的优先级；处理括号
2. 后缀表达式：ABCD-x+EF/- 已考虑 运算符优先级，无括号

后缀表达式

• 组成：只有 操作数 + 运算符；
• 表达：原运算式 对应 的表达式树 的后续遍历
• 计算表达式值：

1. 初始设置一个空栈，****顺序扫描 ****后缀表达式
2. 若为操作数，则压入栈
3. 若为操作符<op>，则连续*从 栈中 退出 两个操作数Y和*X*，形成 运算指令X<op>Y，计算*结果**** 重新 压入栈
4. 所有表达式 项 都扫描完， 栈顶 即为 结果

中缀 转换为 前/后缀：（手工）

1. 按运算符优先级，对所有运算单位 加（）
2. 运算符 移到 相应 的（）前/后面
3. 去掉括号

中缀 转换为 后缀：以a*b+(-c)为例

1. 根本：栈存放 暂时 不能确定 运算次序的 操作符

2. 算法思想：

3. 从左到右 扫描 中缀表达式

4. 扫到 数，加入后缀

5. 扫到 符：

6. ‘（’：入栈

7. ‘）’：栈内运算符依次 出栈，直至栈内遇到‘（’，然后 直接删除‘（’

8. 其他运算符：优先级 ＞ 栈顶的非‘（’运算符时or栈空or栈顶‘(’，直接入栈

否则，依次弹出 当前处理 符 ≤ 栈内优先级 的 运算符，

直到遇‘(’or 优先级<当前处理 符

待处理序列

栈

后缀表达式

当前扫描元素

动作

a*b+(-c)

a

a加入后缀表达式

*b+(-c)

a

*入栈

b+(-c)

a

b

b加入后缀表达式

+(-c)

ab

+<栈顶，弹出**

+(-c)

ab

+入栈

(-c)

ab*

(

(入栈

-c)

+(

ab*

栈顶为****(，-入栈****

c)

+(-

ab*

c

c加入后缀表达式

)

+(-

ab*c

)

把栈中****(之后的符号入后缀，并删(****

ab*c-

扫描完毕，运算符依次退栈，入后缀

ab*c-+

完成

1. 具体转换 过程 （在 中缀表达式后+‘****#****’表示 表达式结束，题中 不算 操作符）

操作符

#

（

*****,/****

+,-

）

isp栈内优先

0

1

5

3

6

icp栈外优先

0

6

4

2

1

步骤

扫描项

项类型

动作

栈内

输出

0

‘#’进栈，读下一符号

1

a

操作数

直接输出

a

2

操作符

isp(‘#’)<icp(‘’)，进栈*

#*

3

b

操作数

直接输出

#*

b

4

操作符

isp(‘’)>icp*(‘+’)，退栈并输出

5

isp(‘#’)<icp(‘+’)，进栈

#+

6

（

操作符

isp(‘-’)<icp(‘（’)，进栈

#+（

7

操作符

isp(‘（’)<icp(‘-’)，进栈

#+（-

8

c

操作数

直接输出

#+（-

c

9

）

操作符

isp(‘-’)>icp(‘）’)，退栈并输出

#+（

10

isp(‘（’)==icp(‘）’)，直接退栈

#+

11

操作符

isp(‘+’)>icp(‘#’)，退栈并输出

12

isp(‘#’)==icp(‘#’)，退栈，结束

队列

顺序存储

队非空时，

Q.front指向队头元素的上一个元素，Q.rear指向队尾元素

Q.front指向队头元素，Q.rear指向队尾元素的下一个位置

∵假溢出：初始Q.front==Q.rear=0; “队满”Q.front==Q.rear

∴循环队列

1. 初始Q.front=Q.rear=0;
2. 队长：****(Q.rear-Q.front+MaxSize)%MaxSize****
3. 出队/入队时，Q.front或Q.rear顺时针+1：

x=Q.data[Q.front];

Q.front=(Q.front+1)%MaxSize

链式存储

链队列

1. 优点：不存在队满 甚至 溢出

2. 适用：数据元素波动大，或者 多个队列

3. 队空：

4. 无头结点： Q.rear=NULL，Q.front=NULL

5. 带头结点：Q.front==Q.rear

（带头结点，增删操作统一）

1. 入队：...s->next=NULL...
2. 出队：...Q.front->next=p->next，if(Q.rear==p){ Q.rear=Q.front;}...

树

二叉树

N0=1+N2

满二叉树

1. 结点数：2^h-1

结点i的

1. 父结点：└i/2┘
2. 左孩子结点：2i
3. 右孩子结点：2i+1

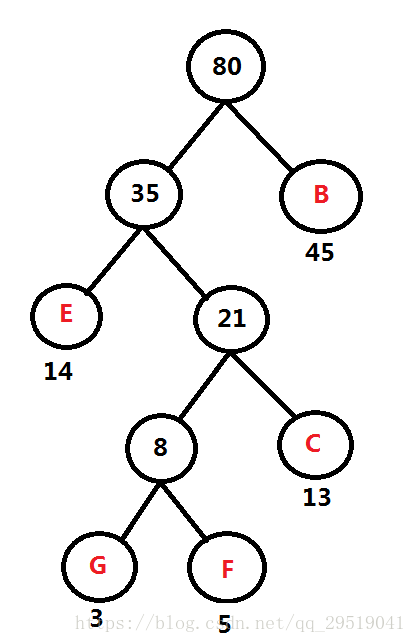
*哈夫曼树（最优二叉树）*Huffman

目的：找出存放一串字符所需的最少的二进制编码

最小的两个合成组成二叉树。在频率表中删去他俩，并加入新的根结点。重复该步骤

默认是小在左，大在右，，所以哈弗曼编码不唯一

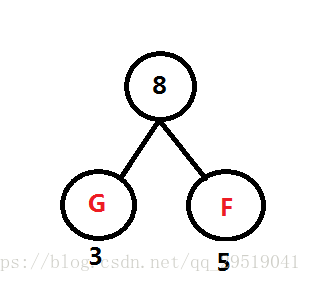
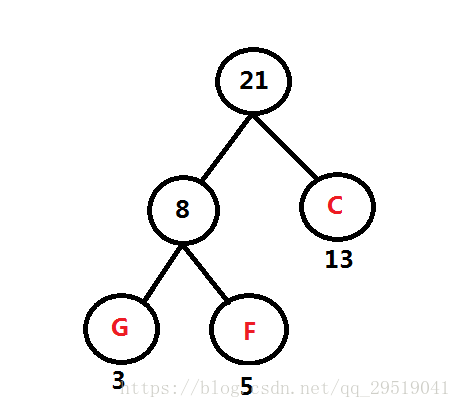
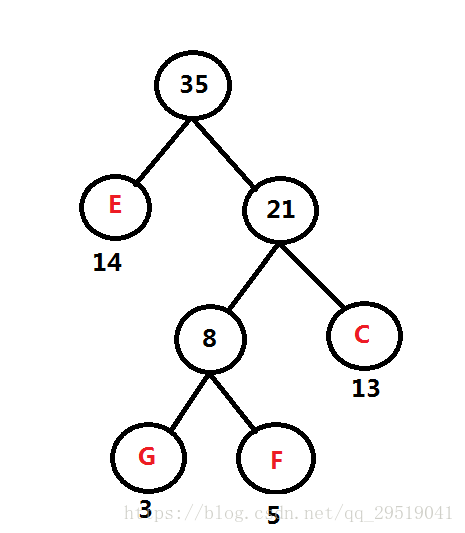
例如：频率表 B:45, C:13 D:69 E:14 F:5 G:3

度m的哈夫曼树只有度为0和m的结点∴Nm=(n-1)/(m-1)

1. 固定长度编码：待处理的字符串序列中，每个字符用同样长度的二进制位
2. 可变长度编码：频率高的字符短编码；平均编码长度 减短，压缩数据
3. 前缀编码：没有一个 编码 是 *另外 一个编码的前缀*
4. 哈夫曼是前缀，可变长度编码

二叉排序树/二叉查找树BST（Binary Search/Sort Tree）

左子树的关键字 ＜****根结点＜****右子树的关键字

判断是否为BST：中序序列递增=>B为BST，即pre < bt->data

平衡二叉树AVL

任一结点的 左子树 和 右子树 的深度之差≤1

插入：若需调整，则每次 调整对象 必为 最小 不平衡二叉树

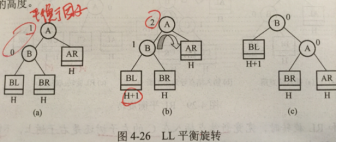
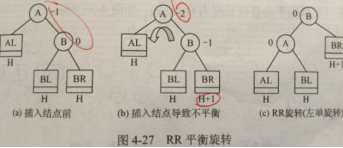
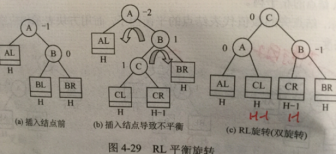
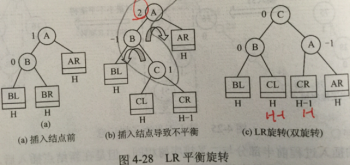
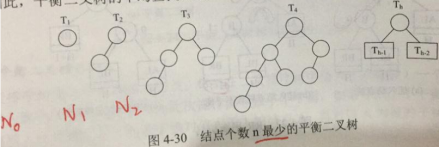
查找：Nh表示深度为h最少结点数，则N0=0，N1=1，N2=2，Nh=Nh-1+Nh-2+1

大根堆

左/右子树的关键字 ≤根结点，完全二叉树

最小生成树

1. 定义：连通，无向带权 图的生成树，权值之和最小的
2. 唯一：当任意环中边的权值相异，则最小生成树唯一

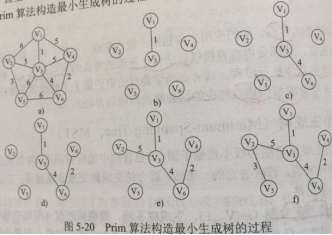
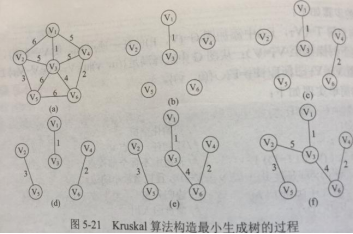
普里姆Prim算法

克鲁斯卡Kruskal算法

共同

基于贪心算法

特点

从顶点开始扩展最小生成树

按权递增次序，选择不构成环的边

T(n)

O(|V|^2)

O(|E|log2|E|)

堆存放E，每次选最小权值边O(log2|E|)****

T所有边看成等价类，每次****+边，看成求等价类∴并查集****描述T，

∴构造T需O(|E|)

适用

稠密图

稀疏图

森林

对应树

森林1次

对应二叉树

先根****遍历

先序遍历

先序遍历

后根****遍历

中序遍历

中序遍历

先序 确定的 二叉树个数

∵先序+中序 可 唯一 确定 一棵二叉树

其关系 就如 入栈序列+出栈序列 可 唯一 确定 一个 栈

∴先序 确定 二叉树个数，即先序 确定 中序个数，

NLR确定LNR，LN、NL相当于压栈，R相当于进了立即出

∴h(n)=Catalan卡特兰数=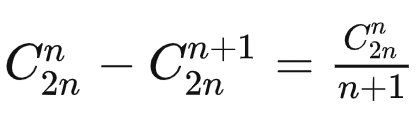

带权路径长度WPL

WPL=∑（weight路径边*数）=(16+21+30)*2+(10+12)*3=200

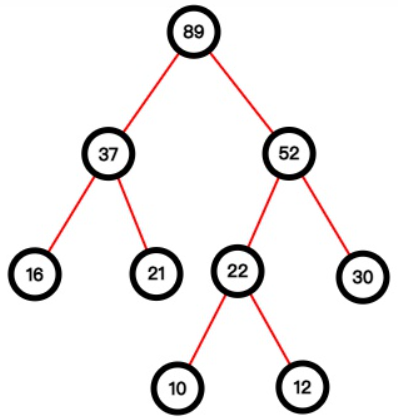
查找次数=路径上的结点数，路径长度=路径上的边数

图

完全图

1. 无向：任意两个顶点间，只有一条边，n(n-1)/2条边
2. 有向：任意两个顶点间，只有****方向相反的两条弧，****n(n-1)****条弧

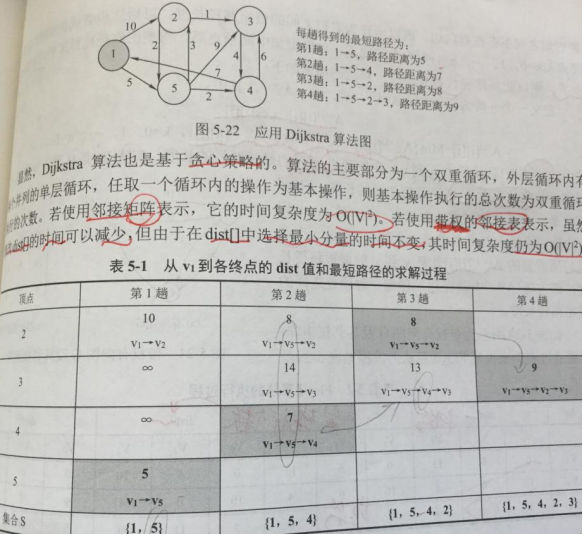
最短路径

Dijkstra算法

Floyd算法

问题

单源最短路径（单起源到各个顶点的最短距离，从源点的临近点开始）

各个顶点之间的最短路径

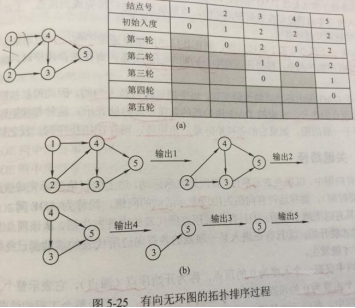
拓扑排序

1. DAG：有向无环图Directed Acycline Graph

2. 拓扑排序：DAG中，每个顶点只出现一次，对每个****<u,v>，序列中，u在v前****

3. 唯一：图为线性有序序列时，唯一；若存在顶点 有多个后继则不唯一

4. 邻接矩阵：

5. 算法：

6. 输出并*删除 一个 没有前驱 的结点*

7. 删除 以该结点 为弧头 的边

8. 重复（1）（2），直到 DAG为空 或者 不存在 无前驱的 结点（环）

关键路径

1. 关键路径：最长路径，工程所需时间

2. 关键活动：最长路径上的边

3. ve(k)：事件k最早发生时间ve(k)=0（源点），ve(k)=Max{ve(j)+Weight(j,k)}

4. vl(k)：事件k最迟发生时间vl(k)=ve(k)（汇点），vl(k)=Min{vl(j)-Weight(j,k)}

5. e(i)：活动ai最早开始时间<vk,vj>，e(i)=vl(k)

6. l(i)：活动ai最迟开始时间<vk,vj>，l(i)=vl(j)-Weight(k,j)

7. d(i)：l(i)-e(i)，为0的即关键活动

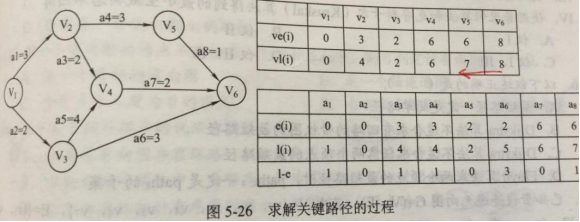
1. 适度缩短 关键活动，可以缩短工期，过度时，关键活动可能变成非关键活动
2. 多关键路径时，缩短 所有 关键路径 才 缩短工期，除非有“桥”---所有关键路径的共有活动

模式匹配

主串S，长n，模式串T，长m。T在S中首次出现的位置

BF模式匹配

最坏T(n)=O(m*************n)

KMP模式匹配

1. next[j]：T的第j个字符失配于S中的第i个字符，需要用T的第next[j]个字符与S中的第i个字符 比较

abcdeabf（f失配，第*next[j]=3个字符c比较）T起点开始*，和失配点结束的最大公共前缀

1. next[1]=0：i++;
2. next[2]**=1，next[j]：i不变;**

模式匹配过程：

1. S中第i个char，T中第j个char
2. j指向 失配点/ j****=****m（全部匹配成功） 为 一趟

虽KMP的T(n)=O(m****+********n)****，

但实际中BF的****T(n)接近O(m+n)****，

∴至今采用

只有T中有很多部分匹配，KMP才明显快

内部排序算法

T(n)和S(n)

1. 任何 基于 比较 的算法，都可用 二叉树 描述判定过程，∴T(n)至少=O(nlog2n)

操作

内部排序

思想

稳定

平均

S(n)

T(n)

平均

最坏

最好

插

入

直接

查找；elem插入到有序，顺序找位

√

1

n****2

n2顺序

n逆序

折半

查找；直接插入的优化，折半找位

x

1

n2与初始序列无关

希尔

分治；分组直接插入排序d个组L[i,i+d,...,i+kd]

x

1

n1.3

n2

依赖f(d)

交换

冒泡

擂台；无序中两两比较，不等则交换，至最值

√

1

n****2

n2逆序

n顺序

快速

分治；取pivot，调整至L[1...k-1]＜L(k)≤L[k+1...n]

x

log2n

nlog2n

n2最不平衡

nlog2n最平衡

选择

简单

擂台；第i趟L[i...n]，初始min=i，swap(L(min),L(i))

x

1

n2

n2逆序

n2顺序

堆

擂台；完全二叉树，根>子结点（大根堆）

x

1

nlog2n

nlog2n逆序

nlog2n顺序

2-路归并

分治；分组排序，两两合并 相邻 有序序列

√

n

nlog2n

nlog2n逆序

nlog2n顺序

基数

多key；从优先级min的开始入队分配，收集

√

r

d(n+r)与初始序列无关

1. 顺序/链式存储 均可：（与 下标 无关）直接插入，冒泡，快速，简单选择，2-路归并

2. 顺序存储：（数组）折半，希尔，堆，基数

3. 比较次数与初始状态无关：简单选择，基数

4. *T(n)与初始序列*无关：折半，堆，多路归并，基数

5. 过程特征：（每一趟确定一个elem最终位置）

6. 第k趟确定第k小/大值：冒泡，堆，简单选择

7. 第k趟确定第i小/大值：快速

应用

1. 考虑因素：

2. n待排序数目

3. elem本身信息量大小

4. key的结构

5. 稳定性要求

6. 语言工具条件

7. 存储结构

8. 辅助空间大小

9. 情况：

10. n≤50 ? 100：n****2

11. 链式存储/n≤50：直接插入

12. 顺序存储：折半插入

13. elem本身信息量大：简单选择（移动少）

14. 1000≥n＞50?100：希尔

15. n＞1000：nlog2n

16. key随机分布：快速排序

17. key位数少且可分解：基数

18. *T(n)与初始序列*无关：

• 辅助空间小：堆
• 稳定：归并

1. key基本有序：（比较：直接插入 < ****冒泡**** ，****移动****：****直接插入****>冒泡）

2. 基本逆序：直接插入

3. 基本顺序：冒泡

4. elem本身信息量大：链式存储；避免耗费 大量移动记录

5. 总体信息量大：归并排序；内存一次放不下，需要外部介质

平均查找长度ASL

顺序 / 线性查找

ASL

无序线性表

有序表

succ

(n+1)/2

fail

n+1

折半 / 二分查找

判定树：描述 折半查找过程

ASLsucc≈log2(n+1)-1

分块 / 索引顺序查找

1. 优点：动态结构，快速查找

2. 基本思想：

3. 块间：第i块max key<第i+1块all key

4. 块内：无序

5. 索引表：含 各块的 max key和各块 第一个元素 地址

6. ASLSucc=LI+LS

7. LI：ASL索引查找

8. LS：ASL块内查找

9. 分b块，每块s个记录：(b+1)/2 + (s+1)/2 =

（索引表，顺序表，均顺序查找）当s=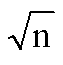时ASLmin=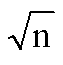+1

1. 若对索引表 折半查找：┌log2(b+1)┐ +(s+1)/2

散列(Hash)表

1. 散列表：根据 关键字 直接访问 的 数据结构
2. 对比：散列表中key和 存储地址 有直接映射关系，而线性表，树表等无确定映射关系
3. 散列函数：Hash(key)=Addr（数组下标，索引，内存地址）
4. 冲突：不同关键字 映射到同一地址
5. 同义词：映射到同一地址的不同关键字
6. *T(n)：无冲突时*，O(1)

散列函数 构造

要求

1. 定义域：全部 关键字
2. 值域：依赖于**** 散列表大小****/地址范围
3. 地址：计算出来的地址 应 等概率，均匀 分布 整个地址空间
4. 计算：简单，以在短时间计算出

方法

Hash(key)

适用

不适/特点

直接****定址

a*key+b

key分布连续

key分布不连续，空位多，则空间浪费

除留****取余

key MOD p

质数p左接近表长m；简单，常用

平方取中

key****2的中间几位

每一位取值都不够均匀

/均＜Addr所需位数

Addr与key的每一位都有关系，

使Addr分布均匀

数字分析

数码分布均匀的几位

已知Key的集合

（r进制，r个数码）

某些位分布不均匀，

只有某几种数码经常出现

折叠

分割成位数相同的几部分，

取这几部分的叠加和

key位数多，且每一位

数字上分布大致均匀

key分成 位数相同的几部分

(最后一部分，可以短些)

处理冲突

1. 定义：同义词 找下一个“空”Hash地址
2. 方法：

*Hi表示冲突后的第i次探测的散列地址，m散列表表长，di增量序列，i∈[1，m-1]

1. 开放地址：Hi=(Hash(key)+di)%m空闲地址 还对 同义词表项开放
2. 线性探测：di=1...di++..di=m-1顺序查看下一单元，直到找到空闲单元/查遍全表

（检测到表尾地址m-1时，下一地址为表首地址0）

可能 大量元素 在相邻 散列地址 堆积，大大降低了查找效率

1. 平方/二次探测：di=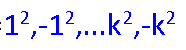（k≤m/2，m为4k+3的质数）；较好，可避免堆积；

不能 检测所有单元，但至少能检测 一半单元

1. 再/双散列：di=Hash2(key)；最多m-1次 探测 遍历全表，回到H0位置

2. 伪随机序列：di=伪随机序列

3. 拉链/链式地址：同义词****链 由 散列地址 唯一标识；适用于 经常增删

ps：

∵查找时，碰到空指针 就认为查找失败

∴开放地址 不能物理删除元素，否则会 截断 其他具有相同 散列地址 的 查找地址；

∴只能做删除标记 ∴ 多次删除后，散列表看起来很满，其实许多位置没用

∴要定期维护散列表，把删除标记的 元素 物理删除

性能分析

1. 决定因素：散列函数；处理冲突的方法；装满因子α=n/m=记录数/表长
2. ASL：与α有关

递归

1. 代码简单，容易理解
2. 缺点：通常 包含很多重复计算，效率不高
3. 精髓：将 原始问题 转换为 属性相似 的 小规模 问题
4. 递归工作栈：容量与 递归调用最大深度一致

递归和递推的区别

• 递归：

1. 设置递归边界
2. 判断已经计算过，直接返回结果
3. 返回关系式

• 递推：

1. 初始化边界
2. 根据初始化边界 开始 递推
3. 循环递推

十进制转换为二进制

余数入栈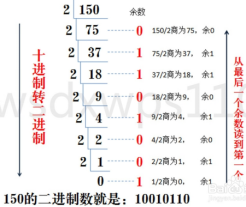

迷宫求解

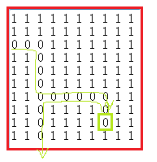
1. 已走过的0改2，且入栈，
2. 坐标周围无0时，出栈直到遇到周围有0

算法（编程题）

场景题千千万，但都是由经典算法变换而来。

优化一般靠牺牲空间换时间

经验

一般过了3道编程，过了1.5就差不多，2就稳了。但是不绝对，有的一道题也会让你面试，有的a了2，也不一定有面试机会
有没有面试机会更多看的是卷的程度，名额多少，简历（例如学历高低）

• 运用示例，摸清规律，弄懂整个逻辑后，再动手
• 10min没有完整思路的先跳过，有时候局限了，回过头可能想得出来
• 随手保存
• 不要追求AC率，后面有空再返回完善，
• 注意题目中说明输入的上限，如下

read_line()//将读取至多1024个字符，一定注意看题目字符上限
gets(n)//将读取至多n个字符，当还未达到n个时如果遇到回车或结束符

常用输出

let a=[1,2,3];

console.log(a.toString());     //1,2,3  arr->str
console.log(a.join(' '));     // 1 2 3  arr->str
console.log(...a);            // 1 2 3  展开运算符...

考核方式

ACM模式

自己构造输入格式，控制返回格式，OJ不会给任何代码，不同的语言有不同的输入输出规范。

JavaScript(V8)

ACMcoder OJ

readline()获取单行字符串

key：

read_line()//将读取至多1024个字符，一定注意看题目字符上限
gets(n)//将读取至多n个字符，当还未达到n个时如果遇到回车或结束符

printsth(sth, ...)//多个参数时，空格分隔；最后不加回车。
console.log(sth, ...)、print(sth, ...)//多个参数时，空格分隔；最后加回车

line.split(' ').map(Number);//str->arr
arr.push([]);//arr[]->arr[][]

//单行输入
while(line=readline()){
    //字符数组
    var lines = line.split(' ');
    //.map(Number)可以直接将字符数组变为数字数组
    var lines = line.split(' ').map(Number);  
    
    var a = parseInt(lines[0]);//效果等同下面
    var b = +lines[1];         //+能将str转换为num
    print(a+b);
}

//矩阵的输入
while (line = readline()) {
    let nums = line.split(' ');//读取第一行
    var row = +nums[0];//第一行的第一个数为行数
    var col = +nums[1];//第一行的第二个数为列数
    var map = [];//用于存放矩阵
    for (let i = 0; i < row; i++) {
        map.push([]);
        let mapline = readline().split(' ');
        for (let j = 0; j < col; j++) {
            map[i][j] = +mapline[j];
        }
    }
}

JavaScript(Node)

华为只可以采用Javascript(Node)

牛客JavaScript Node练习

模板1
var readline = require('readline')
// 创建读取行接口对象
const rl = readline.createInterface({
  input: process.stdin,
  output: process.stdout
})
单行
//监听换行，接受数据
rl.on('line', function(line) {
  //line为输入的单行字符串，split函数--通过空格将该行数据转换为数组。
  var arr= line.split(' ')
  //数组arr的每一项都是字符串格式，如果我们需要整型，则需要parseInt将其转换为数字
  console.log(parseInt(arr[0]) + parseInt(arr[1]));
})

多行
const inputArr = [];//存放输入的数据
rl.on('line', function(line){
  //line是输入的每一行，为字符串格式
    inputArr.push(line.split(' '));//将输入流保存到inputArr中（注意为字符串数组）
}).on('close', function(){
    console.log(fun(inputArr))//调用函数并输出
})

//解决函数
function fun() {
    xxxxxxxx
    return xx
}
模板2
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;

void async function () {
    // Write your code here
    while(line = await readline()){
        let tokens = line.split(' ');
        let a = parseInt(tokens[0]);
        let b = parseInt(tokens[1]);
        console.log(a + b);
    }
}()

核心代码模式

只需要实现函数核心功能并返回结果，无须处理输入输出

例如力扣上是核心代码模式，就是把要处理的数据都已经放入容器里，可以直接写逻辑

链表

判断链表是否有环

key：遍历链表，判断相邻结点是否相等，若结点为空，则false，若相等，则true

function ListNode(x){
   this.val = x;
   this.next = null;
 }

/**
 * 
 * @param head ListNode类 
 * @return bool布尔型
 */
function hasCycle( head ) {
    // write code here
    if(!head || !head.next){return false}
    let fast = head.next
    let slow = head
    while(slow !== fast){
        if(!fast || !fast.next){
            return false
        }
        fast = fast.next.next
        slow = slow.next
    }
    return true
}
module.exports = {
    hasCycle : hasCycle
};

二叉树

(反)序列化二叉树

序列化二叉树，key：

• let arr = Array.isArray(s) ? s : s.split("");
  

• let a = arr.shift();
  

• let node = null;
  

• if (typeof a === "number")
  

function TreeNode(x) {
    this.val = x;
    this.left = null;
    this.right = null;
}
//反序列化二叉树：tree->str 把一棵二叉树按照某种遍历方式的结果以某种格式保存为字符串
function Serialize(pRoot, arr = []) {
    if (!pRoot) {
        arr.push("#");
        return arr;
    } else {
        arr.push(pRoot.val);//注意是val。而不是root
        Serialize(pRoot.left, arr);
        Serialize(pRoot.right, arr);
    }
    return arr;
}
//序列化二叉树：str->tree 根据字符串结果str，重构二叉树
function Deserialize(s) {
    //转换为数组
    let arr = Array.isArray(s) ? s : s.split("");
    //取出val
    let a = arr.shift();
    //构建二叉树结点
    let node = null;
    if (typeof a === "number") {
        //还有可能等于#
        node = new TreeNode(a);
        node.left = Deserialize(arr);
        node.right = Deserialize(arr);
    }
    return node;
}
module.exports = {
    Serialize: Serialize,
    Deserialize: Deserialize,
};

前序遍历（迭代）

入栈：中右左

出栈：中左右

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var preorderTraversal = function(root) {
    let stack=[]
    let res = []
    let cur = null;
    if(!root) return res;
    root&&stack.push(root)
    while(stack.length){
        cur = stack.pop()
        res.push(cur.val)
        cur.right&&stack.push(cur.right)
        cur.left&&stack.push(cur.left)
    }
    return res
};

中序遍历（迭代）

指针的遍历来帮助访问节点，栈则用来处理节点上的元素。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var inorderTraversal = function(root) {
    let stack = []
    let res = []
    let cur = root
    while(cur||stack.length){
        if(cur){
            stack.push(cur)
            cur = cur.left
        } else {
            cur = stack.pop()
            res.push(cur.val)
            cur = cur.right
        }
    }
    return res
};

后序遍历（迭代）

和前序遍历不同：

入栈：中左右

出栈：中右左

rever出栈：左右中

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var postorderTraversal = function(root) {
    let stack = []
    let res = []
    let cur = root
    if(!root) return res
    stack.push(root)
    while(stack.length){
        cur = stack.pop()
        res.push(cur.val)
        cur.left&&stack.push(cur.left)
        cur.right&&stack.push(cur.right)
    }
    return res.reverse()

};

层序遍历

树的层序遍历，相似 图的广度优先搜索

1. 初始设置一个空队，根结点入队
2. 队首结点出队，其左右孩子 依次 入队
3. 若队空，说明 所有结点 已处理完，结束遍历；否则（2)

/*
 * function TreeNode(x) {
 *   this.val = x;
 *   this.left = null;
 *   this.right = null;
 * }
 */

/**
 *
 * @param root TreeNode类
 * @return int整型二维数组
 */
function levelOrder(root) {
    // write code here
    if (root == null) {
        return [];
    }

    const arr = [];
    const queue = [];

    queue.push(root);

    while (queue.length) {
        const preSize = queue.length;
        const floor = [];//当前层
        for (let i = 0; i < preSize; ++i) {
            const v = queue.shift();
            floor.push(v.val);
            v.left&&queue.push(v.left);
            v.right&&queue.push(v.right);
        }
        arr.push(floor);
    }
    return arr;//[[1],[2,3]]
}
module.exports = {
    levelOrder: levelOrder,
};

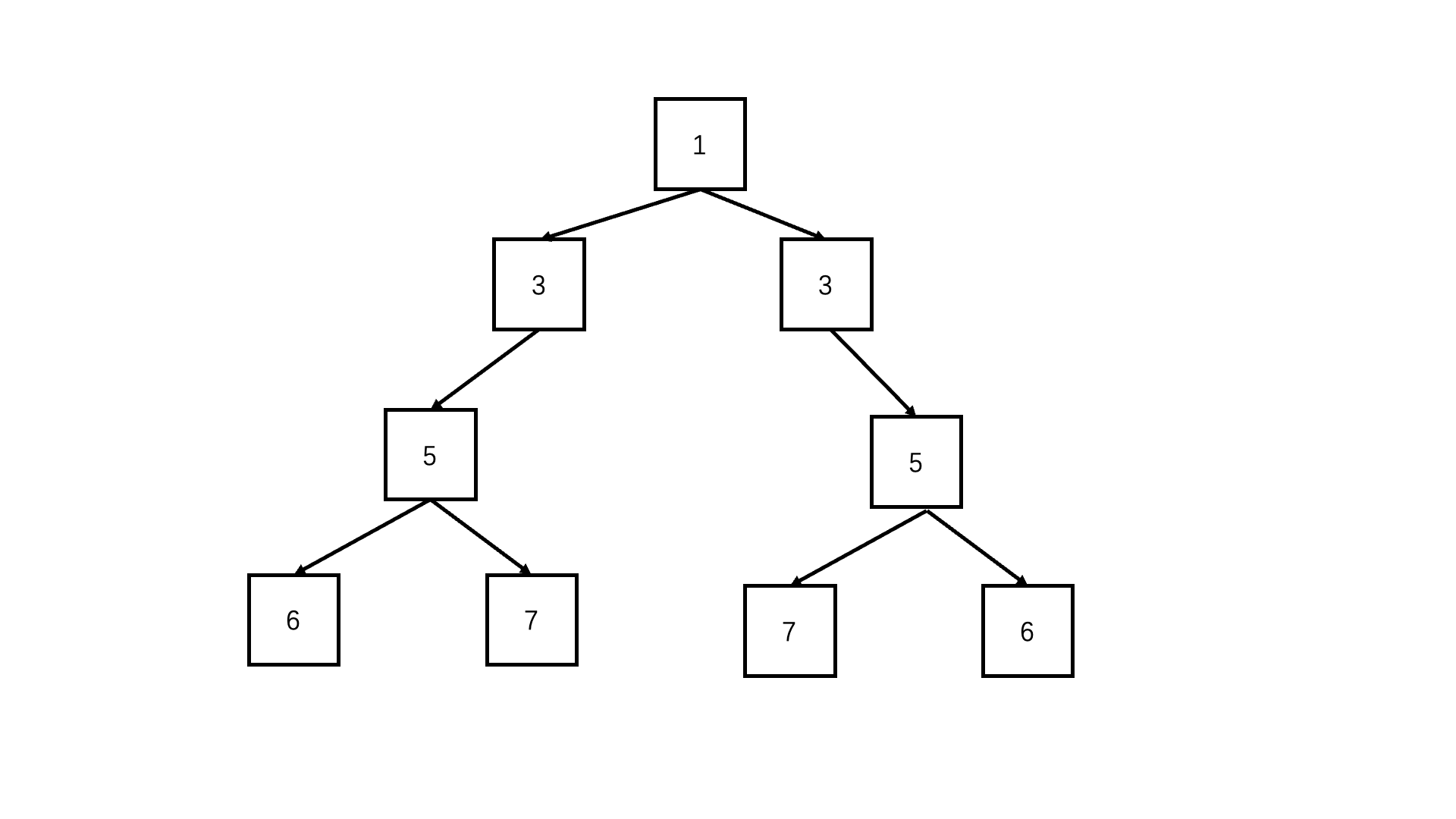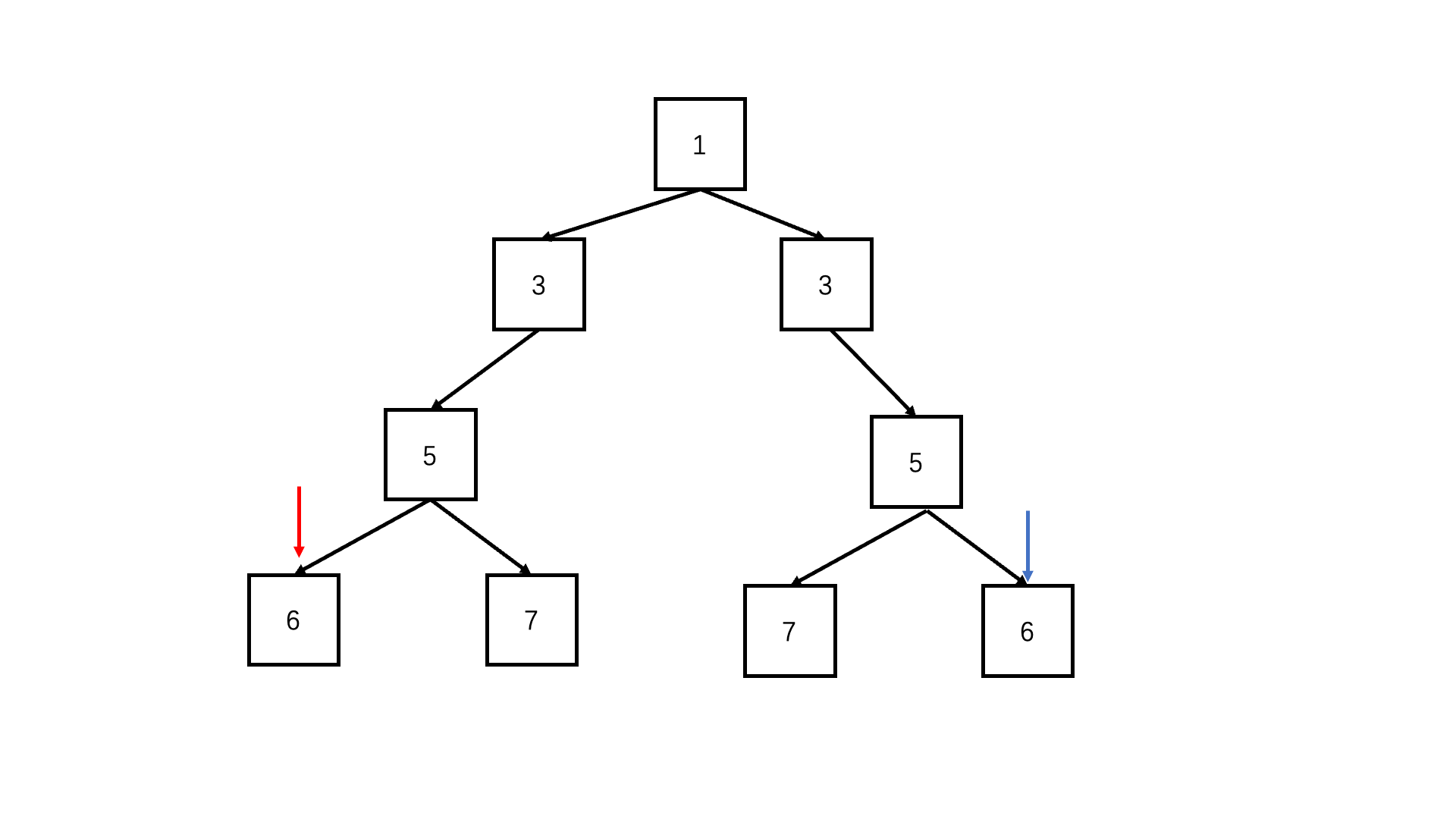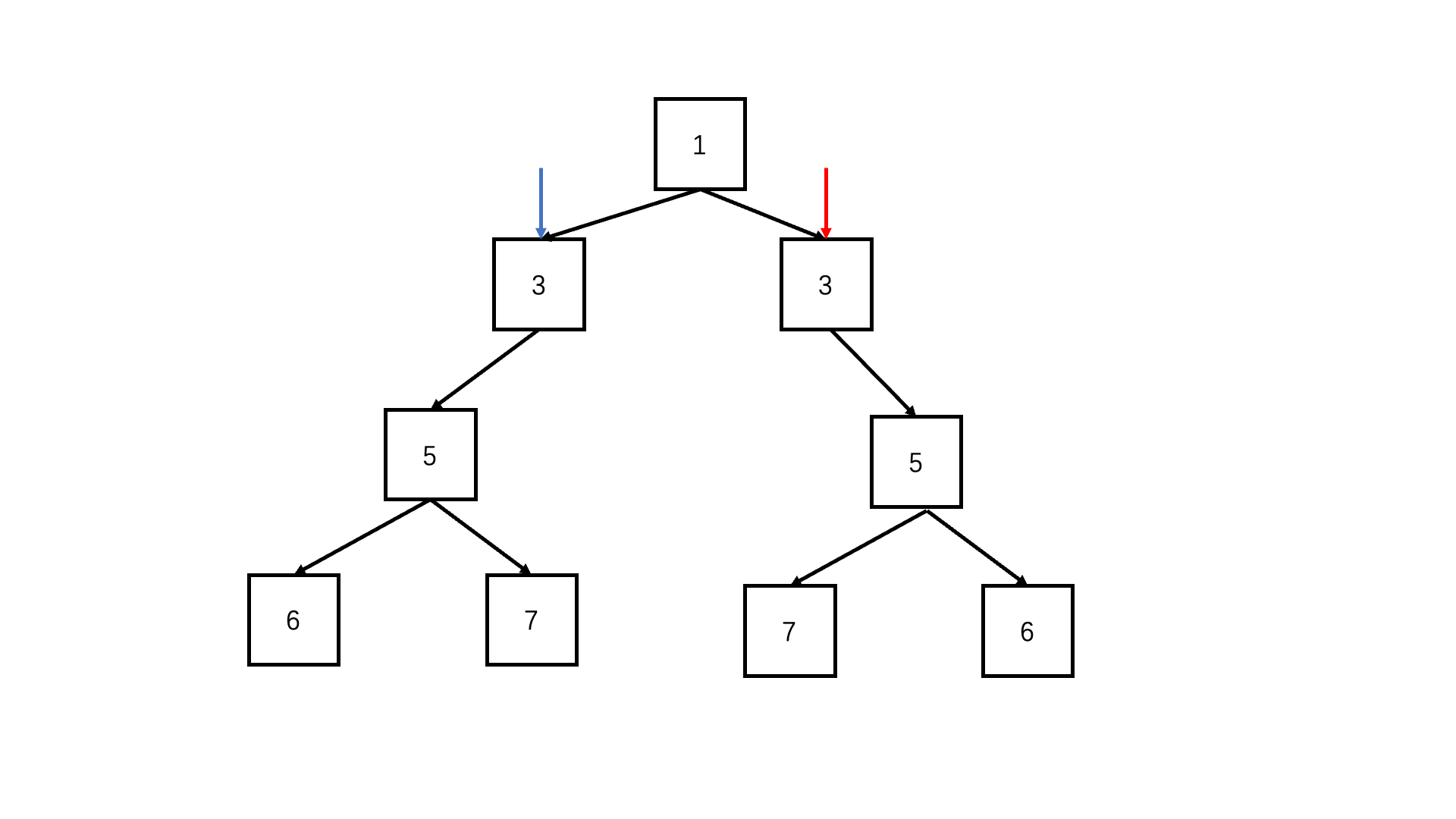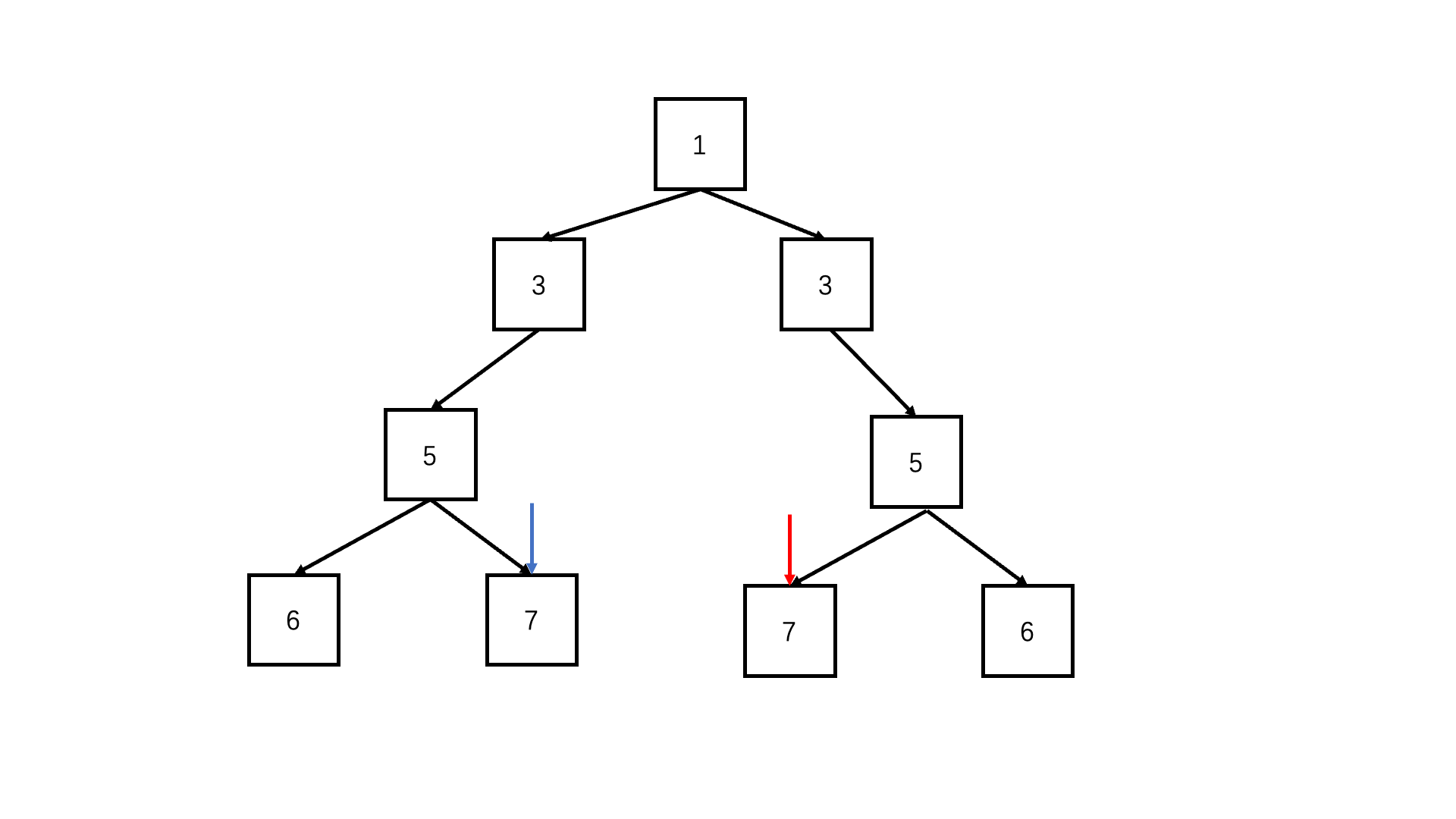
判断对称二叉树

/* function TreeNode(x) {
    this.val = x;
    this.left = null;
    this.right = null;
} */
let flag = true;
function deep(left, right) {
    if (!left && !right) return true; //可以两个都为空
    if (!right||!left|| left.val !== right.val) {//只有一个为空或者节点值不同，必定不对称
        return false;
    }
    return deep(left.left, right.right) && deep(left.right, right.left); //每层对应的节点进入递归比较
}
function isSymmetrical(pRoot) {
    return deep(pRoot, pRoot);
}
module.exports = {
    isSymmetrical: isSymmetrical,
};

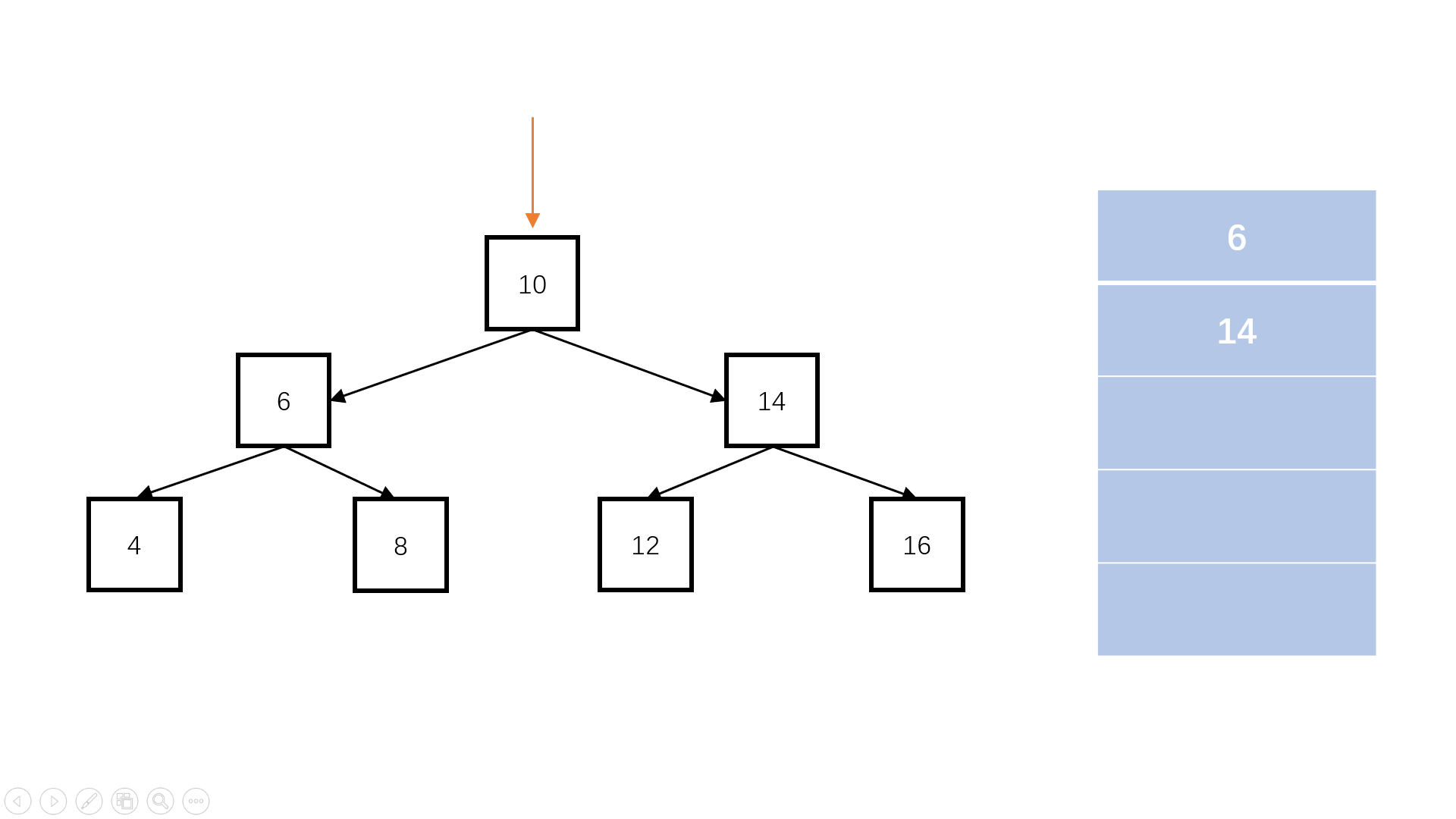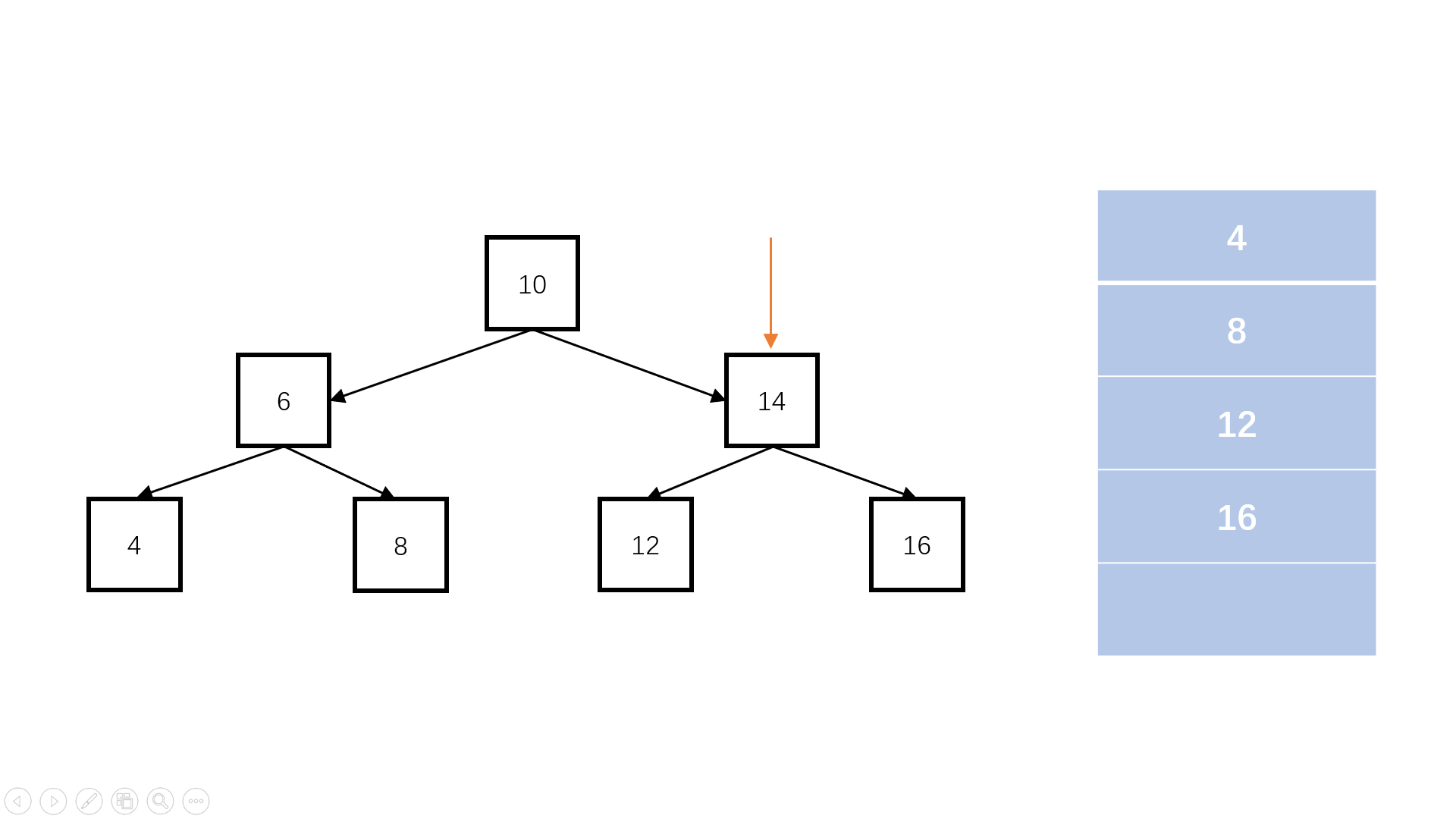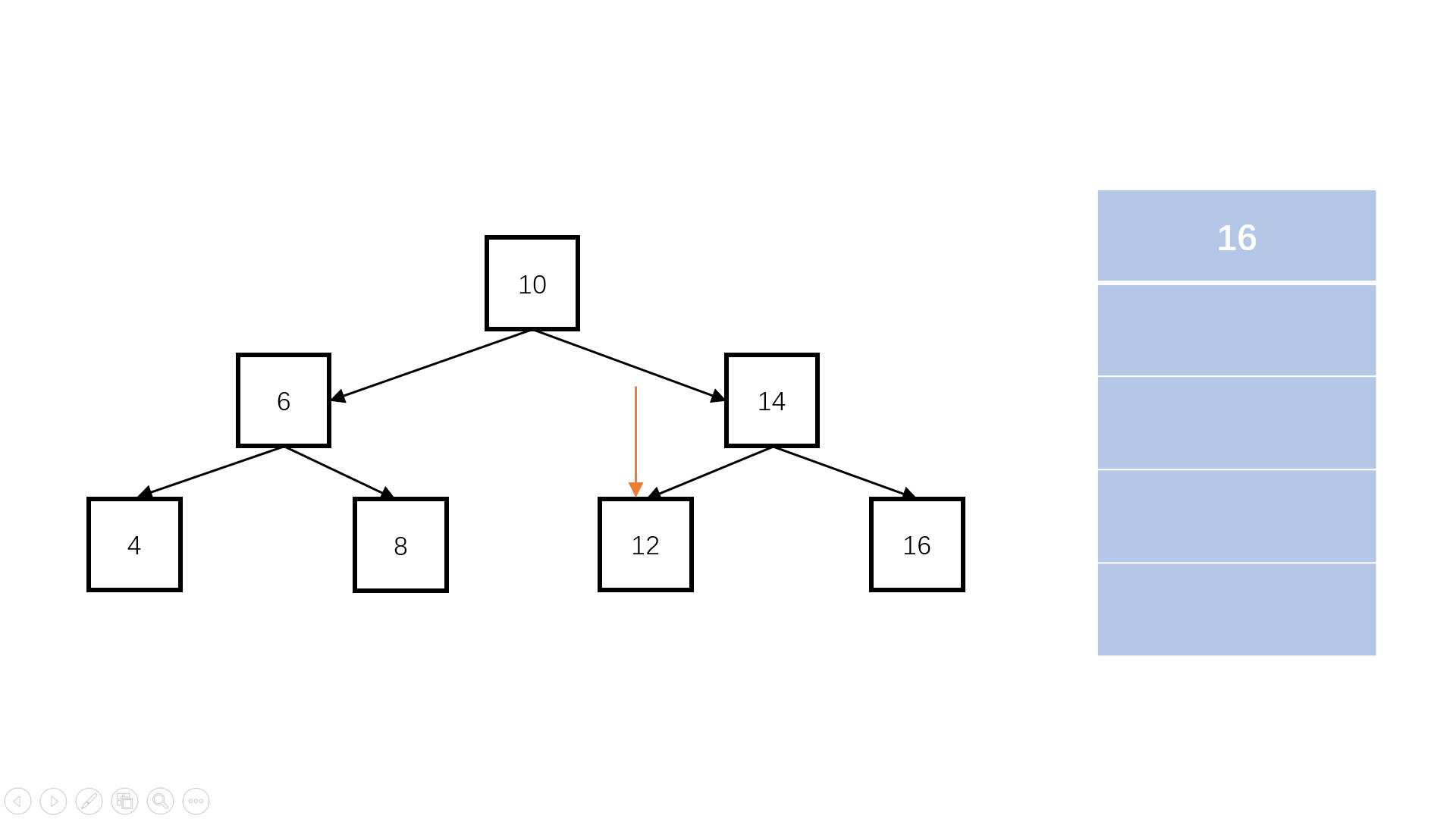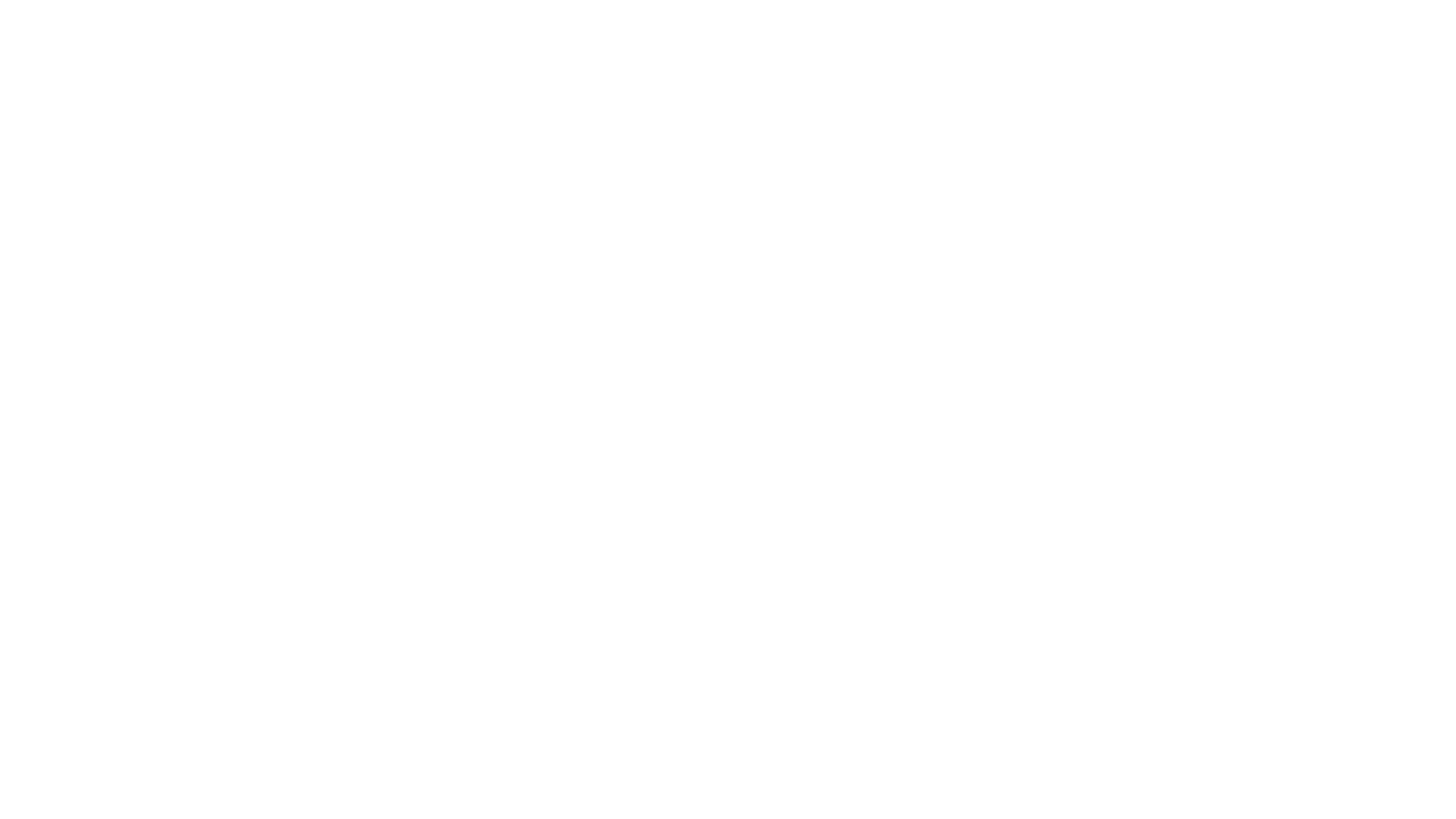
判断完全二叉树

完全二叉树：叶子节点只能出现在最下层和次下层，且最下层的叶子节点集中在树的左部。

/*
 * function TreeNode(x) {
 *   this.val = x;
 *   this.left = null;
 *   this.right = null;
 * }
 */
/**
 * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 *
 *
 * @param root TreeNode类
 * @return bool布尔型
 */
function isCompleteTree(root) {
    // write code here
    if (root == null) return true;

    const queue = [];
    queue.push(root);

    let flag = false; //是否遇到空节点
    while (queue.length) {
        const node = queue.shift();
        if (node == null) {
            //如果遇到某个节点为空，进行标记，代表到了完全二叉树的最下层
            flag = true;
            continue;
        }

        if (flag == true) {
            //若是后续还有访问，则说明提前出现了叶子节点，不符合完全二叉树的性质。
            return false;
        }

        queue.push(node.left);
        queue.push(node.right);
    }
    return true;
}
module.exports = {
    isCompleteTree: isCompleteTree,
};

判断平衡二叉树

平衡二叉树是左子树的高度与右子树的高度差的绝对值小于等于1，同样左子树是平衡二叉树，右子树为平衡二叉树。

/* function TreeNode(x) {
    this.val = x;
    this.left = null;
    this.right = null;
} */
function IsBalanced_Solution(pRoot)
{
    if(!pRoot) return true;
    // write code here
    return (Math.abs(getMaxDepth(pRoot.left) - getMaxDepth(pRoot.right)) <=1) && IsBalanced_Solution(pRoot.left) && IsBalanced_Solution(pRoot.right)
}

function getMaxDepth(root) {
    if(!root) return 0;
    return Math.max(getMaxDepth(root.left)+1,getMaxDepth(root.right)+1)
}
module.exports = {
    IsBalanced_Solution : IsBalanced_Solution
};

二叉树的镜像

先序遍历

/*
 * function TreeNode(x) {
 *   this.val = x;
 *   this.left = null;
 *   this.right = null;
 * }
 */
/**
 * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 *
 * 
 * @param pRoot TreeNode类 
 * @return TreeNode类
 */
function Mirror( pRoot ) {
    
    function traversal(root){
        if(root===null) return ;
        //交换左右孩子
        let temp = root.left;
        root.left = root.right;
        root.right = temp;

        traversal(root.left);
        traversal(root.right);
        return root;
    }
    
    return traversal(pRoot);
    // write code here
}
module.exports = {
    Mirror : Mirror
};

最近公共祖先

如果从两个节点往上找，每个节点都往上走，一直走到根节点，那么根节点到这两个节点的连线肯定有相交的地方，

如果从上往下走，那么最后一次相交的节点就是他们的最近公共祖先节点。

/*
 * function TreeNode(x) {
 *   this.val = x;
 *   this.left = null;
 *   this.right = null;
 * }
 */

/**
 *
 * @param root TreeNode类
 * @param o1 int整型
 * @param o2 int整型
 * @return int整型
 */
function dfs(root, o1, o2) {
    if (root == null || root.val == o1 || root.val == o2) {
        return root;
    }
    //递归遍历左子树
    let left = dfs(root.left, o1, o2);
    //递归遍历右子树
    let right = dfs(root.right, o1, o2);
    //如果left、right都不为空，那么代表o1、o2在root的两侧，所以root为他们的公共祖先
    if (left && right) return root;
    //如果left、right有一个为空，那么就返回不为空的那一个
    return left != null ? left : right;
}

数组和树

扁平结构(一维数组)转树

key：

1. pid：parent id
2. obj[item.id] = { ...item, children: [] }
3. pid === 0
4. !obj[pid]
5. obj[pid].children.push(treeitem)

   //pid：parent id 
   let arr = [
        { id: 1, name: '部门1', pid: 0 },
        { id: 2, name: '部门2', pid: 1 },
        { id: 3, name: '部门3', pid: 1 },
        { id: 4, name: '部门4', pid: 3 },
        { id: 5, name: '部门5', pid: 4 },
    ]

    // // 上面的数据转换为 下面的 tree 数据
    // [
    //     {
    //         "id": 1,
    //         "name": "部门1",
    //         "pid": 0,
    //         "children": [
    //             {
    //                 "id": 2,
    //                 "name": "部门2",
    //                 "pid": 1,
    //                 "children": []
    //             },
    //             {
    //                 "id": 3,
    //                 "name": "部门3",
    //                 "pid": 1,
    //                 "children": [
    //                     {
    //                         id: 4,
    //                         name: '部门4',
    //                         pid: 3,
    //                         "children": [
    //                             {
    //                                 id: 5,
    //                                 name: '部门5',
    //                                 pid: 4,
    //                                 "children": []
    //                             },
    //                         ]
    //                     },
    //                 ]
    //             }
    //         ]
    //     }
    // ]

    function tree(items) {
        // 1、声明一个数组和一个对象 用来存储数据
        let arr = []
        let obj = {}
        // 2、给每条item添加children ，并连带一起放在obj对象里
        for (let item of items) {
            obj[item.id] = { ...item, children: [] }
        }
        // 3、for of 逻辑处理
        for (let item of items) {
            // 4、把数据里面的id 取出来赋值 方便下一步的操作
            let id = item.id
            let pid = item.pid
            // 5、根据 id  将 obj 里面的每一项数据取出来
            let treeitem = obj[id]
            // 6、如果是第一项的话 吧treeitem 放到 arr 数组当中
            if (pid === 0) {
                // 把数据放到 arr 数组里面
                arr.push(treeitem)
            } else {
                // 如果没有 pid 找不到 就开一个 obj { }
                if (!obj[pid]) {
                    obj = {
                        children: []
                    }
                }

                // 否则给它的 obj 根基 pid（自己定义的下标） 进行查找 它里面的children属性 然后push
                obj[pid].children.push(treeitem)
            }
        }
        // 返回处理好的数据
        return arr
    }
    console.log(tree(arr))

数组扁平化

要求将数组参数中的多维数组扩展为一维数组并返回该数组。
数组参数中仅包含数组类型和数字类型

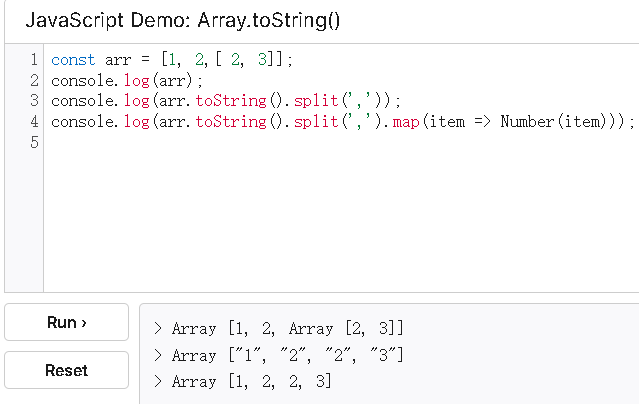
function flatten(arr){
    // toString() + split() 实现   
    return arr.toString().split(',').map(item => Number(item));

    //join() + split() 实现
    return arr.join(',').split(',').map(item => Number(item));

    //reduce 实现
    return arr.reduce((target, item) => {
        return target.concat(Array.isArray(item) ? flatten(item) : item);
    }, [])

    // 递归实现
    let res = [];
    arr.forEach(item => {
        if (Array.isArray(item)) {
            res = res.concat(flatten(item))
      } else {
             res.push(item);
         }
     });
     return res;

    // 扩展运算符实现
       while(arr.some(item => Array.isArray(item))){
         arr = [].concat(...arr);
     }
     return arr;

    // flat()实现（这里不支持使用）
    return arr.flat(Infinity);
}

排序

快速排序

快速排序的基本思想是通过分治来使一部分均比另一部分小（大）再使两部分重复该步骤而实现有序的排列。核心步骤有：

1. 选择一个基准值（pivot）
2. 以基准值将数组分割为两部分
3. 递归分割之后的数组直到数组为空或只有一个元素为止

key：

1. pivot = array.splice(pivotIndex, 1)[0]
2. _quickSort(left).concat([pivot], _quickSort(right))

const _quickSort = array => {
    if(array.length <= 1) return array
    var pivotIndex = Math.floor(array.length / 2)
    var pivot = array.splice(pivotIndex, 1)[0]
    var left = []
    var right = []
    for (var i=0 ; i<array.length ; i++){
        if (array[i] < pivot) {
            left.push(array[i])
        } else {
            right.push(array[i])
        }
    }
    return _quickSort(left).concat([pivot], _quickSort(right))
}

*归并排序

思想：两个/两个以上有序表 合并成 新 有序表

• 2路-归并排序：两两归并
• key：

1. left=arr.slice(0,mid)
2. mergeLeft=mergeSort(left)
3. res.push(leftArr.shift())
4. res=res.concat(leftArr)

 function   mergesort(arr){
            if(arr.length<2)return  arr
            let  len=arr.length
            let  mid=parseInt(len/2)
            let l1=arr.slice(0,mid)
            let  r1=arr.slice(mid,len)
            let  mergeleft=mergesort(l1)
            let mergeright=mergesort(r1)
            return merge(mergeleft,mergeright)
            function merge(left,right){
                let res=[]
                while(left.length!=0 &&right.length!=0){
                    if(left[0]<=right[0]){
                        res.push(left.shift())
                    }else{
                        res.push((right.shift()))
                    }
                }
                if(left.length){
                    res=res.concat(left)
                }
                if(right.length){
                    res=res.concat(right)
                }
                return  res
            }
         
    }

*堆排序

1.首先将待排序的数组构造成一个大根堆，此时，整个数组的最大值就是堆结构的顶端

2.将顶端的数与末尾的数交换，此时，末尾的数为最大值，剩余待排序数组个数为n-1

3.将剩余的n-1个数再构造成大根堆，再将顶端数与n-1位置的数交换，如此反复执行，便能得到有序数组

注意:升序用大根堆，降序就用小根堆(默认为升序)

key：

headAdjust：

1. for (var i = 2 * start + 1; i <= end; i = i * 2 + 1)
2. if (i < end && arr[i] < arr[i-1])

buildHeap：//从最后一棵子树开始,从后往前调整

1. //最大元素保存于尾部，并且不参与后面的调整
2. //进行调整，将最大元素调整至堆顶
3. headAdjust(arr, 0, i);

//每次调整,从上往下调整
//调整为大根堆
function headAdjust(arr, start, end){    
  //将当前节点值进行保存
  var tmp = arr[start];
  //遍历孩子结点
  for (var  i = 2 * start + 1; i <= end; i = i * 2 + 1)
    {
        if (i < end && arr[i] < arr[i-1])//有右孩子并且左孩子小于右孩子
        {
            i--;//i一定是左右孩子的最大值
        }
        if (arr[i] > tmp)
        {
            arr[start] = arr[i];
            start = i;
        }
        else
        {
            break;
        }
    }
    arr[start] = tmp ;
  }
}
//构建堆
function buildHeap(arr){
//从最后一棵子树开始,从后往前调整

  for(var i=  Math.floor(arr.length/2) ; i>=0; i--){
    headAdjust(arr, i, arr.length);
  }
}
function heapSort(arr){
  //构建堆
  buildHeap(arr);
  for(var i=arr.length-1; i>0; i--){
    //最大元素保存于尾部，并且不参与后面的调整
    var swap = arr[i];
    arr[i] = arr[0];
    arr[0] = swap;
    //进行调整，将最大元素调整至堆顶
    headAdjust(arr, 0, i);
  }
}

回溯

如果不能成功，那么返回的时候我们就还要把这个位置还原。这就是回溯算法，也是试探算法。

全排列

通过回溯剪枝。修剪掉有当前元素的path，最后保留与原字符串长度相等的所有元素。

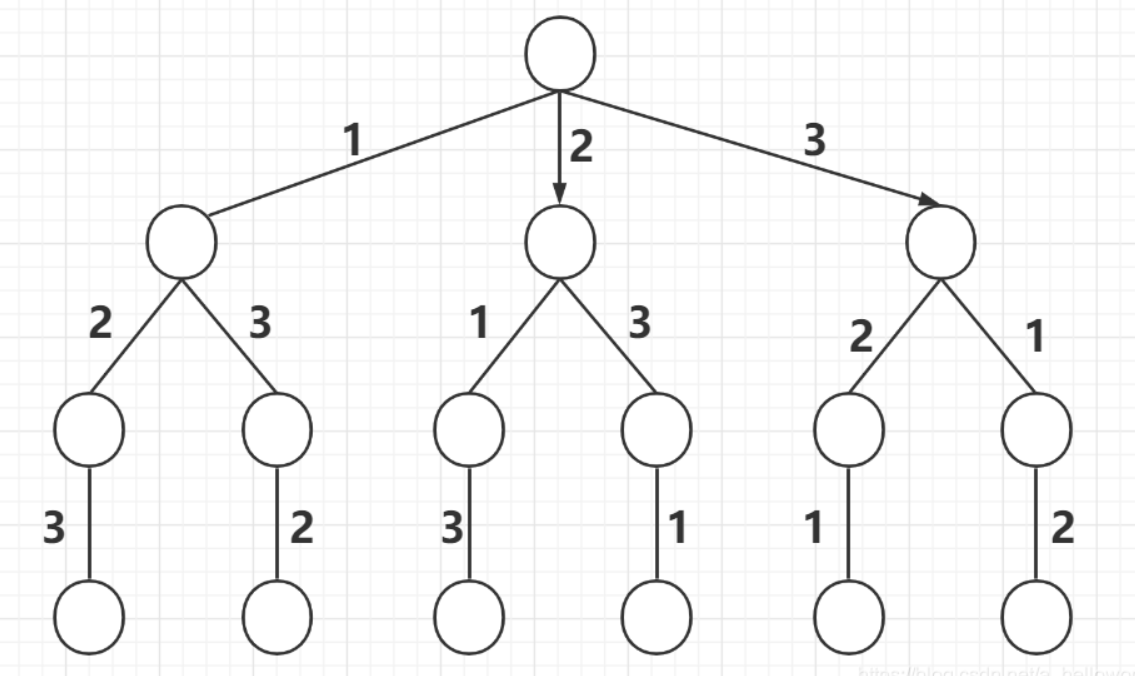
key：

1. path.length == string.length
2. path.includes(item)

const _permute = string => {
    const res = [];
    const backtrace = path => {
        if(path.length == string.length){
            res.push(path);
            return;
        }
        for(const item of string) {
            if(path.includes(item)) continue;
            backtrace(path + item);
        }
    };
    backtrace('');
    return res;
}

N皇后

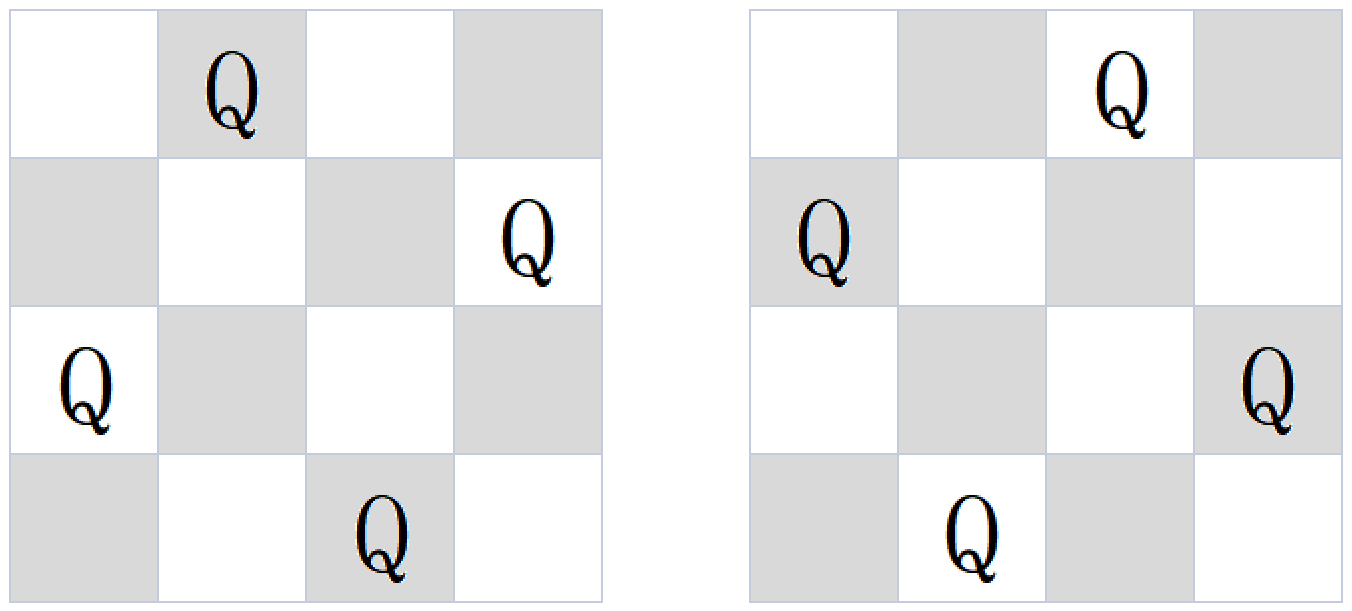
N 皇后问题是指在 n * n 的棋盘上要摆 n 个皇后，
要求：任何两个皇后不同行，不同列也不在同一条斜线上，
求给一个整数 n ，返回 n 皇后的摆法数。

要求：空间复杂度 O(1) ，时间复杂度O(n!)

1. 要确定皇后的位置，其实就是确定列的位置，因为行已经固定了
2. 进一步讲，也就是如何摆放 数组arr [0,1,2,3,...,n-1]
3. 如果没有【不在同一条斜线上】要求，这题其实只是单纯的全排列问题
4. 在全排列的基础上，根据N皇后的问题，去除一些结果

• arr n个皇后的列位置
• res n皇后排列结果
• ruler 记录对应的列位置是否已经占用（也是是否有皇后），如果有，那么设为1，没有设为0
• setPos 哈希集合，标记正斜线（从左上到右下）位置，如果在相同正斜线上，坐标(x,y)满足 y-x 都相同
• setCon 哈希集合，标记反正斜线（从y右上到左下）位置，如果在相同反斜线上，坐标(x,y)满足 x+y 都相同
• 是否在同一斜线上，其实就是这两个点的所形成的斜线的斜率是否为±1。点P(a,b) ，点Q(c,d)（1）斜率为1 (d-b)/(c-a) = 1，横纵坐标之差相等（2）斜率为-1 (d-b)/(c-a) = -1 ，等式两边恒等变形 a+b = c + d ，横纵坐标之和相等

/**
 *
 * @param n int整型 the n
 * @return int整型
 */
function Nqueen(n) {
    let res = []; //二维数组，存放每行Q的列坐标
    let isQ = new Array(n).fill(0); //记录该列是否有Q
    let setPos = new Set(); //标记正对角线
    let setCon = new Set(); // 标记反对角线
    //给当前row找一个col
    const backTrace = (row, path) => {
        if (path.length === n) {
            res.push(path);
            return;
        }
        for (let col = 0; col < n; col++) {
            if (
                isQ[col] == 0 &&
                !setPos.has(row - col) &&
                !setCon.has(row + col)
            ) {
                path.push(col);
                isQ[col] = 1;
                setPos.add(row - col);
                setCon.add(row + col);
                backTrace(row + 1, path);
                path.pop();
                isQ[col] = 0;
                setPos.delete(row - col);
                setCon.delete(row + col);
            }
        }
    };
    backTrace(0, []);
    return res.length;
}
module.exports = {
    Nqueen: Nqueen,
};

动态规划(Dynamic Programming，DP)

用来解决一类最优化问题的算法思想。考虑最简单的情况，以及下一级情况和它的关系
简单来说，动态规划将一个复杂的问题分解成若干个子问题，通过综合子问题的最优解来得到原问题的最优解。需要注意的是，动态规划会将每个求解过的子问题的解记录下来，这样
一般可以使用递归或者递推的写法来实现动态规划，其中递归写法在此处又称作记忆化搜索。

斐波那契(Fibonacci）数列（递归）

function F(n){
if(n= 0||n== 1) return 1;
else return F(n-1)+F(n-2);
}

dp[n]=-1表示F(n)当前还没有被计算过

function F(n) {
if(n == 0lIn-1) return 1;//递归边界
if(dp[n] != -1) return dp[n]; //已经计算过，直接返回结果，不再重复计算else {
else dp[n] = F(n-1) + F(n-2); 1/计算F(n)，并保存至dp[n]
return dp [n];//返回F(n)的结果
}

数塔（递推）

第i层有i个数字。现在要从第一层走到第n层，最后将路径上所有数字相加后得到的和最大是多少?

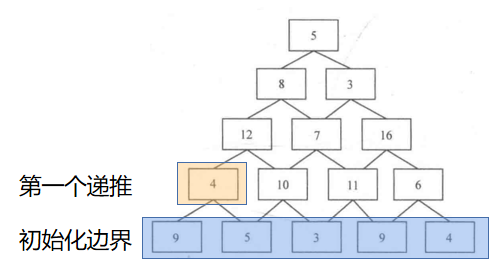
dp[i][j]表示从第i行第j个数字出发到达最底层的所有路径中能得到的最大和

dp[i][i]=max(dp[i-1][j],dp[i-1][j+1])+f[i][j]

最长公共子序列(LCS)

Longest Common Subsequence：子序列可以不连续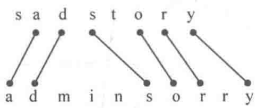
“sadstory”与“adminsorry”最长公共子序列为“adsory”

dp[i][j]表示字符串A的i号位和字符串B的j号位之前的LCS 长度下标从1开始)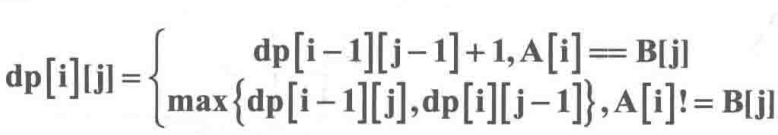

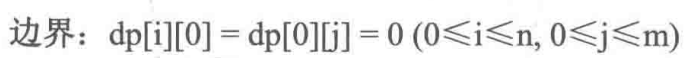
最长回文子串

dp[i][j]表示S[i]至S[j]所表示的子串是否是回文子串，是则为1，不是为0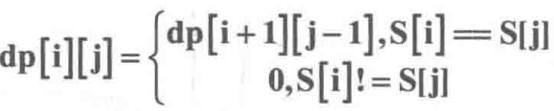

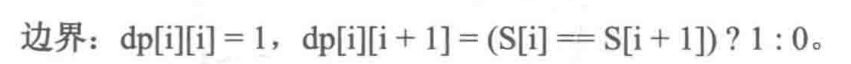
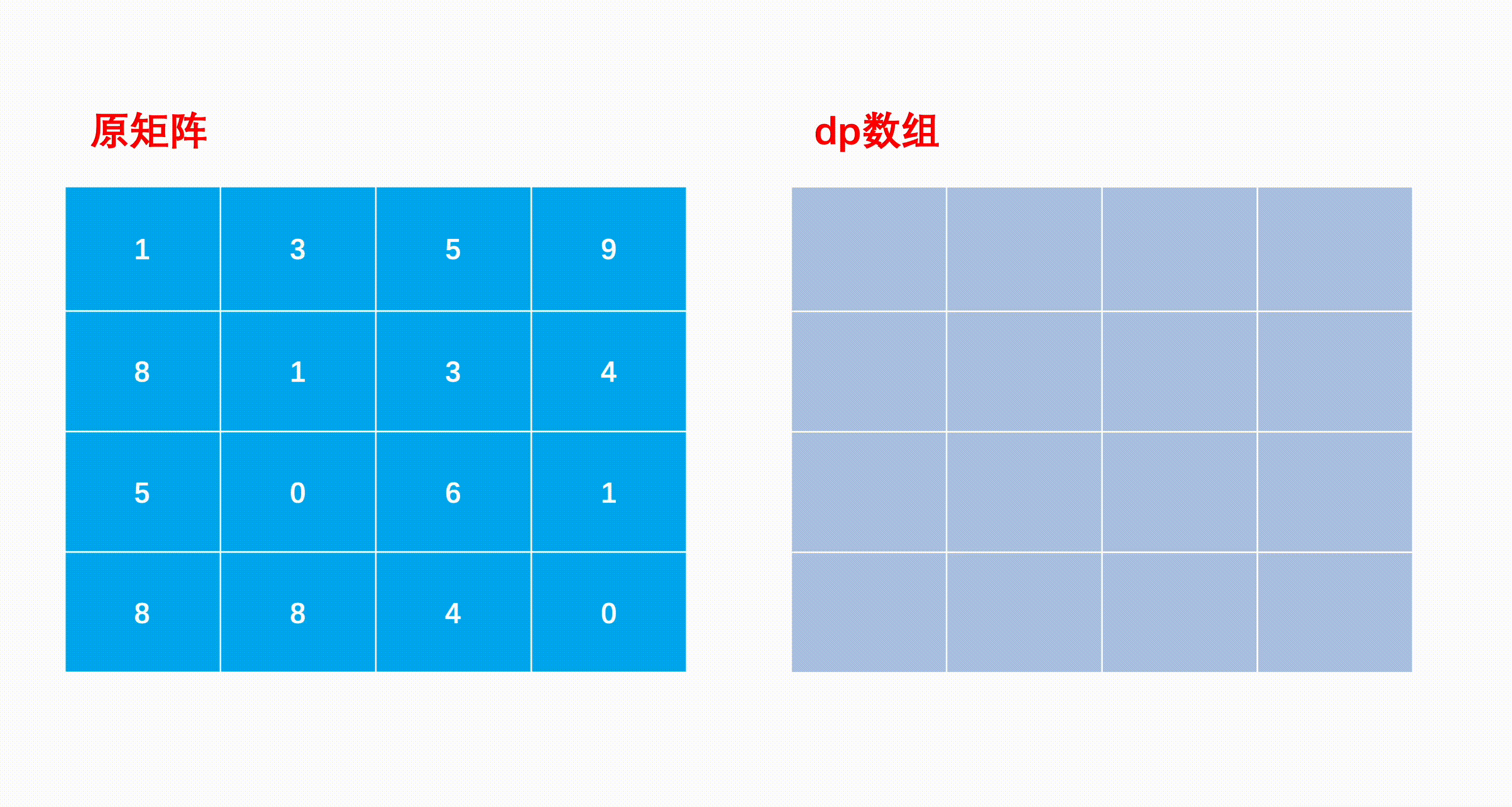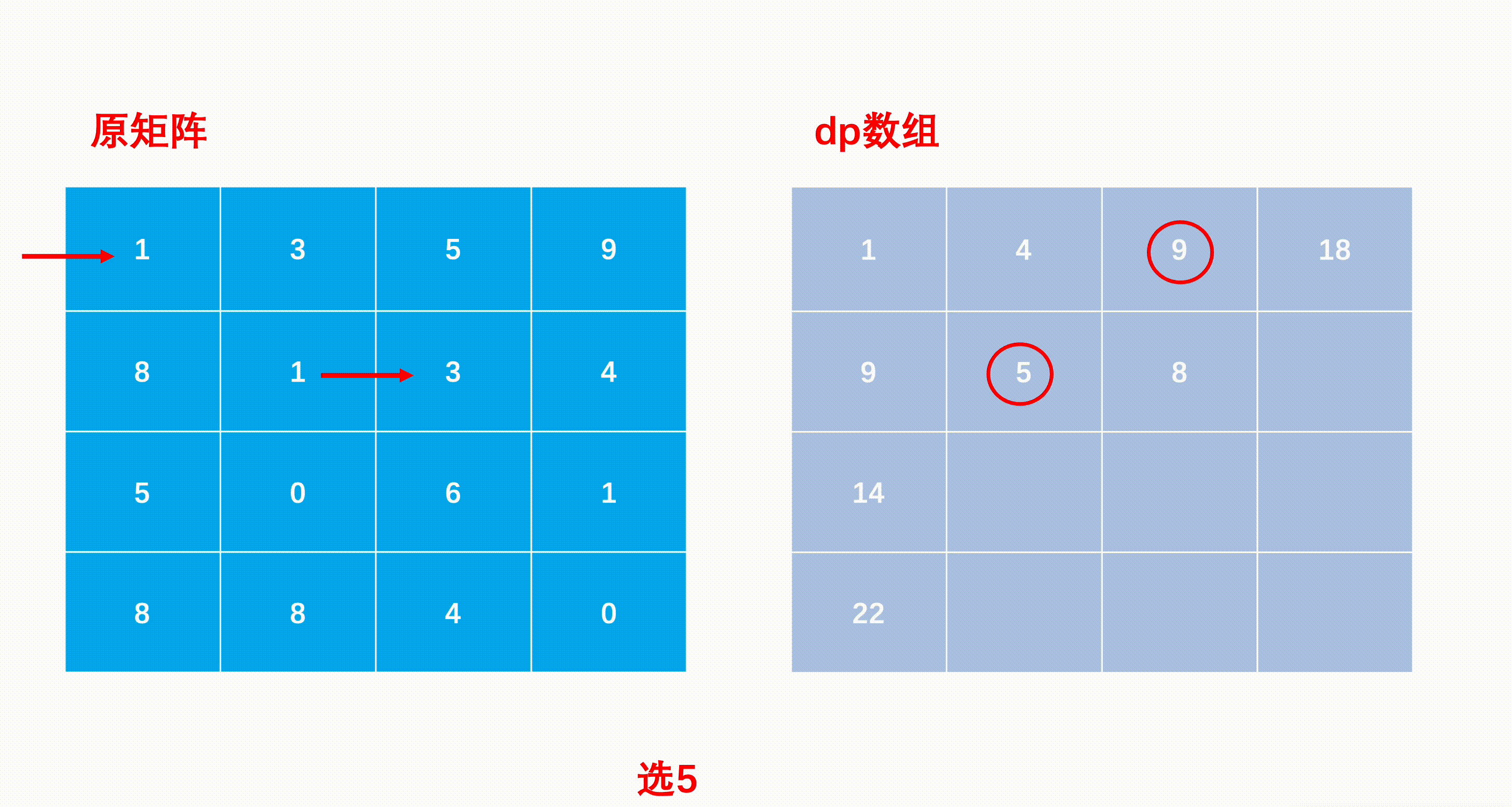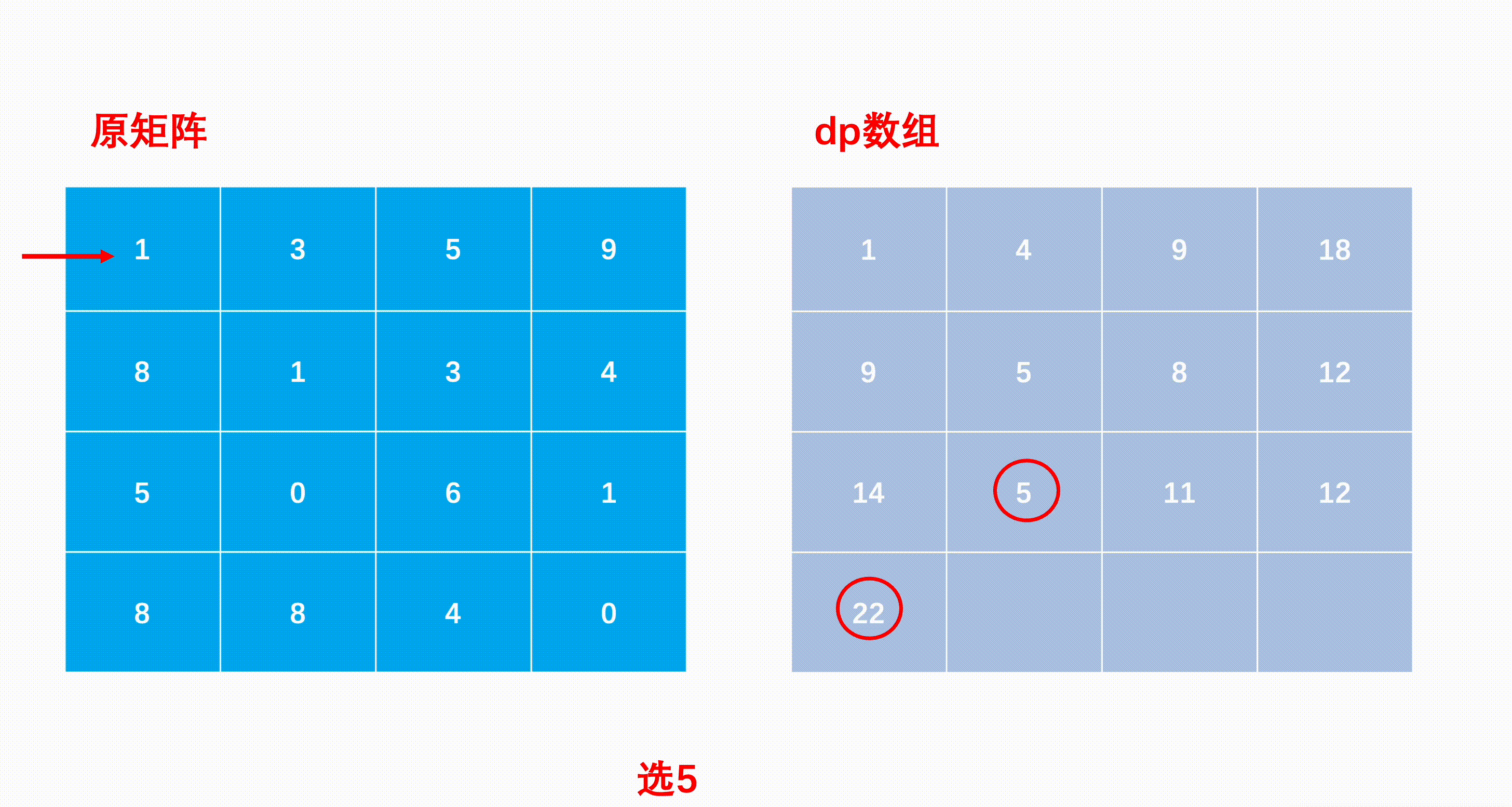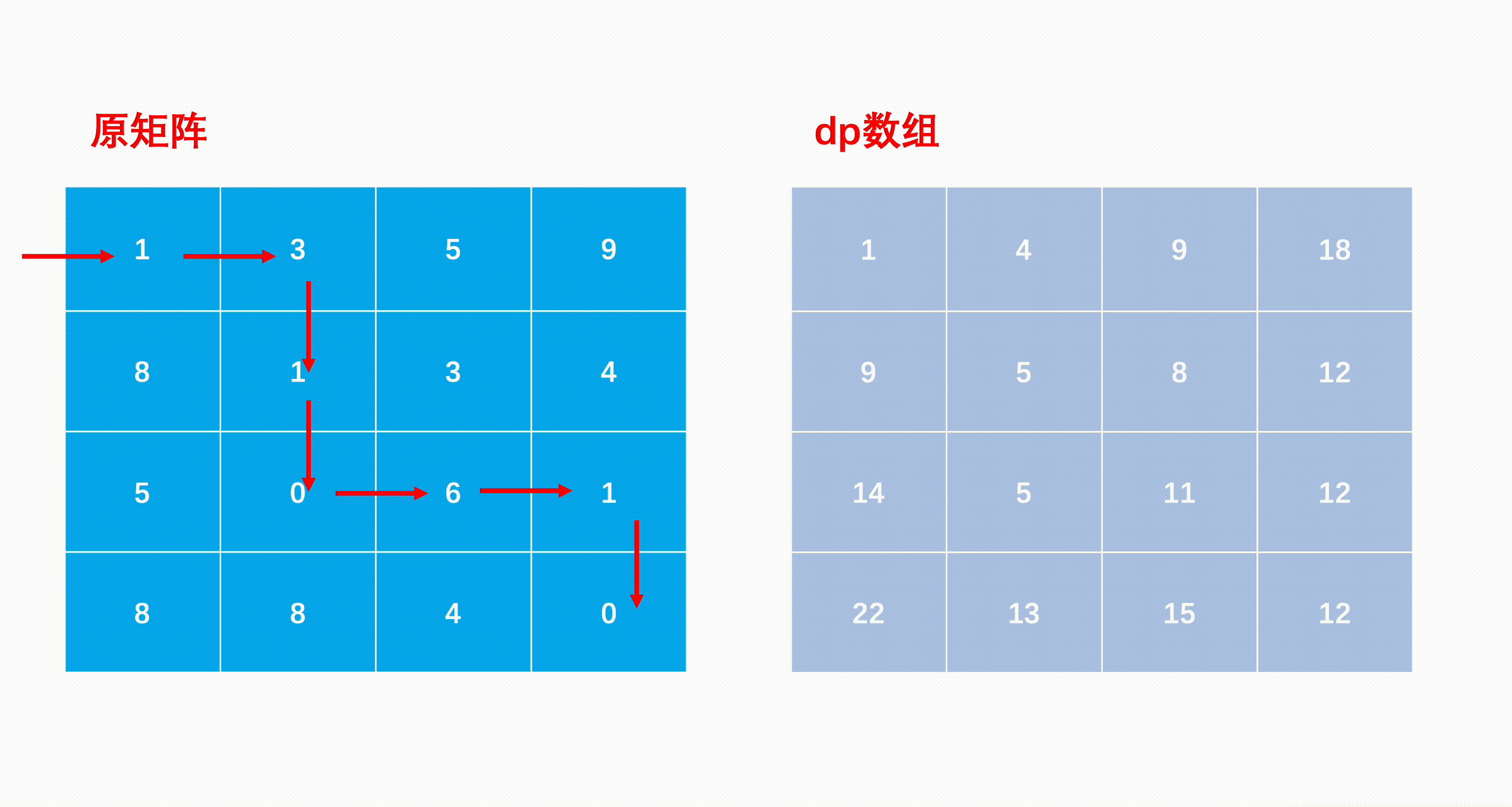
最小路径和

mxn矩阵 a，从左上角开始每次只能向右或者向下走，最后到达右下角的位置，路径上所有的数字累加起来就是路径和，输出所有的路径中最小的路径和。

dp[i][j]代表i到j的最短路径

求解子问题时的状态转移方程：从「上一状态」到「下一状态」的递推式。

dp[i, j] = min(dp[i - 1][j], dp[i][j - 1]) + matrix[i][j]

JavaScript中没有二维数组的概念，但是可以设置数组元素的值等于数组

key：

1. dp[0][i] = dp[0][i - 1] + matrix[0][i];
2. dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + matrix[i][j];

function minPathSum(matrix) {
    var row = matrix.length,
        col = matrix[0].length;
    var dp = new Array(row).fill(null).map(() => new Array(col).fill(0));
    dp[0][0] = matrix[0][0]; // 初始化左上角元素
    // 初始化第一行
    for (var i = 1; i < col; i++) dp[0][i] = dp[0][i - 1] + matrix[0][i];
    // 初始化第一列
    for (var j = 1; j < row; j++) dp[j][0] = dp[j - 1][0] + matrix[j][0];
    // 动态规划
    for (var i = 1; i < row; i++) {
        for (var j = 1; j < col; j++) {
            dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + matrix[i][j];
        }
    }
    return dp[row - 1][col - 1]; // 右下角元素结果即为答案
}

背包

01背包

有n件物品,每件物品的重量为w[i],价值为c[j]。现有一个容量为V的背包，问如何选取物品放入背包，使得背包内物品的总价值最大。其中每种物品都只有1件。
dp[i][v]表示前i件物品(1≤i≤n, 0≤v≤V)恰好装入容量为v的背包中所能获得的最大价值。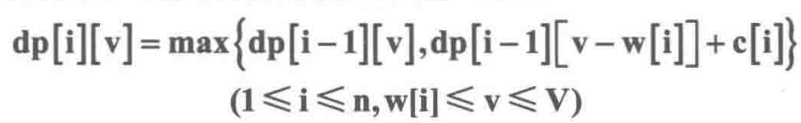

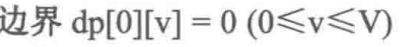
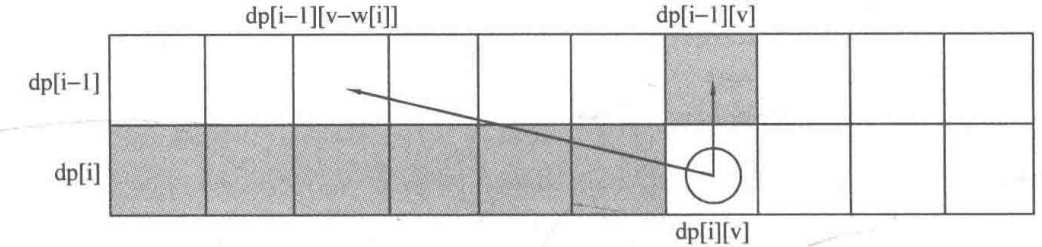
这样修改对应到图中可以这样理解:v的枚举顺序变为从右往左，dp[i][v]右边的部分为刚计算过的需要保存给下一行使用的数据，而dp[i][v]左上角的阴影部分为当前需要使用的部分。将这两者结合一下，即把 dp[i][v]左上角和右边的部分放在一个数组里，每计算出一个dp[i][v]，就相当于把 dp[i - 1][v]抹消，因为在后面的运算中 dp[i- 1][v]再也用不到了。我们把这种技巧称为滚动数组。

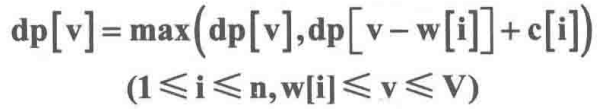
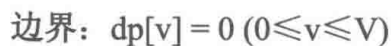
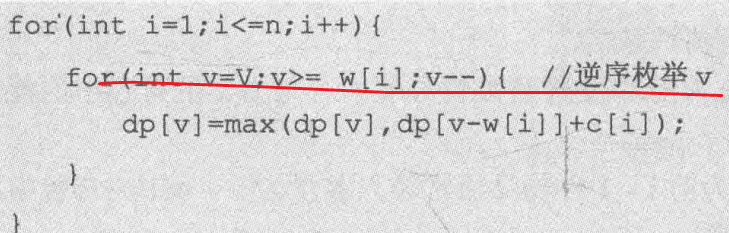
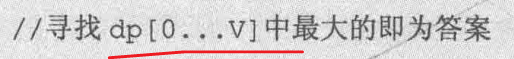
特别说明:

如果是用二维数组存放，v的枚举是顺序还是逆序都无所谓;

如果使用一维数组存放,则v的枚举必须是逆序!

完全背包

与01背包问题不同的是其中每种物品都有无数件。

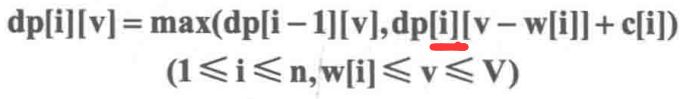
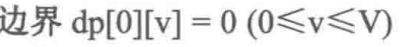
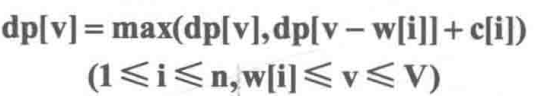
写成一维形式之后和01背包完全相同，唯一的区别在于这里v的枚举顺序是正向枚举，而01背包的一维形式中v必须是逆向枚举。

散列/哈希Hash

空间换时间,即当读入的数为x时，就令hashTable[x]=true(说明: hashTable数组需要初始化为false，表示初始状态下所有数都未出现过)。

数字千位分割

  const format = (n) => {
        let num = n.toString() // 拿到传进来的 number 数字 进行 toString
        let len = num.length // 在拿到字符串的长度
        // 当传进来的结果小于 3 也就是 千位还把结果返回出去 小于3 不足以分割
        if (len < 3) {
            return num
        } else {
            let render = len % 3 //传入 number 的长度 是否能被 3 整除
            console.log(render)

            if (render > 0) { // 说明不是3的整数倍
                return num.slice(0, render) + ',' + num.slice(render, len).match(/\d{3}/g).join(',')
            } else {
                return num.slice(0, len).match(/\d{3}/g).join(',')
            }
        }
    }

    let str = format(298000)
    console.log(str)

常用方法

异或运算^

按位异或，相同为0，不同为1

运算法则：

1.交换律（随便换像乘一样）：a ^ b ^ c === a ^ c ^ b

2.任何数于0异或为任何数 0 ^ n === n

3.相同的数异或为0: n ^ n === 0

Math

//e=2.718281828459045
Math.E;

//绝对值
Math.abs()

//基数（base）的指数（exponent）次幂，即 base^exponent。
Math.pow(base, exponent)

//max,min不支持传递数组
Math.max(value0, value1, /* … ,*/ valueN)
Math.max.apply(null,array)
apply会将一个数组装换为一个参数接一个参数
null是因为没有对象去调用这个方法,只需要用这个方法运算

//取整
Math.floor()  向下取一个整数（floor地板）
Math.ceil(x)  向上取一个整数（ceil天花板）

Math.round() 返回一个四舍五入的值

Math.trunc() 直接去除小数点后面的值

Number

0B，0O为ES6新增

• 二进制：有前缀0b（或**0B）的数值，出现0,1以外的数字会报错**（b：binary）
• 八进制：有前缀0o（或**0O**）的数值，或者是以0后面再跟一个数字（0-7）。如果超出了前面所述的数值范围，则会忽略第一个数字0，视为十进制数（o：octonary）
• 注意：八进制字面量在严格模式下是无效的，会导致支持该模式的JavaScript引擎抛出错误
• 十六进制：有前缀0x，后跟任何十六进制数字（09及AF），字母大小写都可以，超出范围会报错

特殊值：

• Number.MIN_VALUE：5e-324
• Number.MAX_VALUE：1.7976931348623157e+308
• Infinity ，代表无穷大，如果数字超过最大值，js会返回Infinity，这称为正向溢出(overflow)；
• -Infinity ，代表无穷小，小于任何数值，如果等于或超过最小负值-1023（即非常接近0），js会直接把这个数转为0，这称为负向溢出(underflow)
• NaN ，Not a number，代表一个非数值
• isNaN()：用来判断一个变量是否为非数字的类型，如果是数字返回false;如果不是数字返回true。
• isFinite()：数值是不是有穷的

var result = Number.MAX_VALUE + Number.MAX_VALUE;

console.log(isFinite(result)); //false

• typeof NaN // 'number' ---NaN不是独立的数据类型，而是一个特殊数值，它的数据类型依然属于Number``````
• NaN === NaN // false　　 ---NaN不等于任何值，包括它本身
• (1 / +0) === (1 / -0) // false　　---除以正零得到+Infinity，除以负零得到-Infinity，这两者是不相等的

科学计数法：

对于那些极大极小的数值，可以用e表示法（即科学计数法）表示的浮点数值表示。

等于e前面的数值乘以10的指数次幂

numObj.toFixed(digits)//用定点表示法来格式化一个数值

function financial(x) {
  return Number.parseFloat(x).toFixed(2);
}

console.log(financial(123.456));
// Expected output: "123.46"

console.log(financial(0.004));
// Expected output: "0.00"

console.log(financial('1.23e+5'));
// Expected output: "123000.00"

取余是数学中的概念，

取模是计算机中的概念，

两者都是求两数相除的余数

1.当两数符号相同时，结果相同，比如：7%4 与 7 Mod 4 结果都是3

2.当两数符号不同时，结果不同，比如 (-7)%4=-3和(-7)Mod4=1

取余运算，求商采用fix 函数，向0方向舍入，取 -1。因此 (-7) % 4 商 -1 余数为 -3
取模运算，求商采用 floor 函数，向无穷小方向舍入，取 -2。因此 (-7) Mod 4 商 -2 余数为 1

key：((n % m) + m) % m;

Number.prototype.mod = function(n) {
    return ((this % n) + n) % n;
}
// 或 
function mod(n, m) {
  return ((n % m) + m) % m;
}

Map

保存键值对，任何值（对象或者基本类型）都可以作为一个键或一个值。

Map的键可以是任意值，包括函数、对象或任意基本类型。
object的键必须是一个String或是Symbol 。

const contacts = new Map()
contacts.set('Jessie', {phone: "213-555-1234", address: "123 N 1st Ave"})
contacts.has('Jessie') // true
contacts.get('Hilary') // undefined
contacts.delete('Jessie') // true
console.log(contacts.size) // 1

function logMapElements(value, key, map) {
  console.log(`m[${key}] = ${value}`);
}

new Map([['foo', 3], ['bar', {}], ['baz', undefined]])
  .forEach(logMapElements);

// Expected output: "m[foo] = 3"
// Expected output: "m[bar] = [object Object]"
// Expected output: "m[baz] = undefined"

Set

值的集合，且值唯一

let setPos = new Set(); 
setPos.add(value);//Boolean
setPos.has(value);
setPos.delete(value);

function logSetElements(value1, value2, set) {
  console.log(`s[${value1}] = ${value2}`);
}

new Set(['foo', 'bar', undefined]).forEach(logSetElements);

// Expected output: "s[foo] = foo"
// Expected output: "s[bar] = bar"
// Expected output: "s[undefined] = undefined"

set判断值相等的机制

//Set用===判断是否相等
const set= new Set();
const obj1={ x: 10, y: 20 },obj2={ x: 10, y: 20 }
set.add(obj1).add(obj2);

console.log(obj1===obj2);//false
console.log(set.size);// 2

set.add(obj1);
console.log(obj1===obj1);//true
console.log(set.size);//3

数组去重 （⭐手写）

// Use to remove duplicate elements from the array
const numbers = [2,3,4,4,2,3,3,4,4,5,5,6,6,7,5,32,3,4,5]
console.log([...new Set(numbers)])
// [2, 3, 4, 5, 6, 7, 32]

Array

//创建字符串
//join() 方法将一个数组（或一个类数组对象）的所有元素连接成一个字符串并返回这个字符串，用逗号
或指定的分隔符字符串分隔。如果数组只有一个元素，那么将返回该元素而不使用分隔符。
Array.join()
Array.join(separator)

//################创建数组：
//伪数组转成数组
Array.from(arrayLike, mapFn)
console.log(Array.from('foo'));
// Expected output: Array ["f", "o", "o"]

console.log(Array.from([1, 2, 3], x => x + x));
// Expected output: Array [2, 4, 6]

console.log( Array.from({length:3},(item, index)=> index) );// 列的位置
// Expected output:Array [0, 1, 2]

//################原数组会改变：

arr.reverse()//返回翻转后的数组

// 无函数
arr.sort()//默认排序顺序是在将元素转换为字符串，然后比较它们的 UTF-16
// 比较函数
arr.sort(compareFn)
function compareFn(a, b) {
  if (在某些排序规则中，a 小于 b) {
    return -1;
  }
  if (在这一排序规则下，a 大于 b) {
    return 1;
  }
  // a 一定等于 b
  return 0;
}
//升序
function compareNumbers(a, b) {
  return a - b;
}

//固定值填充
arr.fill(value)
arr.fill(value, start)
arr.fill(value, start, end)

//去除
array.shift() //从数组中删除第一个元素，并返回该元素的值。

array.pop() //从数组中删除最后一个元素，并返回该元素的值。此方法会更改数组的长度。
array.push() //将一个或多个元素添加到数组的末尾，并返回该数组的新长度

//unshift() 方法将一个或多个元素添加到数组的开头，并返回该数组的新长度
array.unshift(element0, element1, /* … ,*/ elementN)

//粘接，通过删除或替换现有元素或者原地添加新的元素来修改数组，并以数组形式返回被修改的内容。
array.splice(start)
array.splice(start, deleteCount)
array.splice(start, deleteCount, item1)
array.splice(start, deleteCount, item1, item2...itemN)

//################原数组不会改变：

//切片，浅拷贝（包括 begin，不包括end）。
array.slice()
array.slice(start)
array.slice(start, end)

//展平，按照一个可指定的深度递归遍历数组，并将所有元素与遍历到的子数组中的元素合并为一个新数组返回。
array.flat()//不写参数默认一维
array.flat(depth)

//过滤器，函数体 为 条件语句
// 箭头函数
filter((element) => { /* … */ } )
filter((element, index) => { /* … */ } )
filter((element, index, array) => { /* … */ } )
array.filter(str => str .length > 6) 

//遍历数组处理
// 箭头函数
map((element) => { /* … */ })
map((element, index) => { /* … */ })
map((element, index, array) => { /* … */ })
array.map(el => Math.pow(el,2))
//map和filter同参

//接收一个函数作为累加器，数组中的每个值（从左到右）开始缩减，最终计算为一个值。
// 箭头函数
reduce((previousValue, currentValue) => { /* … */ } )
reduce((previousValue, currentValue, currentIndex) => { /* … */ } )
reduce((previousValue, currentValue, currentIndex, array) => { /* … */ } )
reduce((previousValue, currentValue) => { /* … */ } , initialValue)
reduce((previousValue, currentValue, currentIndex) => { /* … */ } , initialValue)
array.reduce((previousValue, currentValue, currentIndex, array) => { /* … */ }, initialValue)

//一个“reducer”函数，包含四个参数：
//previousValue：上一次调用 callbackFn 时的返回值。
//在第一次调用时，若指定了初始值 initialValue，其值则为 initialValue，
//否则为数组索引为 0 的元素 array[0]。

//currentValue：数组中正在处理的元素。
//在第一次调用时，若指定了初始值 initialValue，其值则为数组索引为 0 的元素 array[0]，
//否则为 array[1]。

//currentIndex：数组中正在处理的元素的索引。
//若指定了初始值 initialValue，则起始索引号为 0，否则从索引 1 起始。

//array：用于遍历的数组。

//initialValue 可选
//作为第一次调用 callback 函数时参数 previousValue 的值。
//若指定了初始值 initialValue，则 currentValue 则将使用数组第一个元素；
//否则 previousValue 将使用数组第一个元素，而 currentValue 将使用数组第二个元素。
const array1 = [1, 2, 3, 4];

// 0 + 1 + 2 + 3 + 4
const initialValue = 0;
const sumWithInitial = array1.reduce(
  (accumulator, currentValue) => accumulator + currentValue,
  initialValue
);

console.log(sumWithInitial);
// Expected output: 10

String

str.charAt(index)//获取第n位字符  
str.charCodeAt(n)//获取第n位UTF-16字符编码 （Unicode）A是65，a是97
String.fromCharCode(num1[, ...[, numN]])//根据UTF编码创建字符串

String.fromCharCode('a'.charCodeAt(0))='a'

str.trim()//返回去掉首尾的空白字符后的新字符串

str.split(separator)//返回一个以指定分隔符出现位置分隔而成的一个数组，数组元素不包含分隔符

const str = 'The quick brown fox jumps over the lazy dog.';

const words = str.split(' ');
console.log(words[3]);
// Expected output: "fox"

str.toLowerCase( )//字符串转小写；
str.toUpperCase( )//字符串转大写；

str.concat(str2, [, ...strN])

str.substring(indexStart[, indexEnd])  //提取从 indexStart 到 indexEnd（不包括）之间的字符。
str.substr(start[, length]) //没有严格被废弃 (as in "removed from the Web standards"), 但它被认作是遗留的函数并且可以的话应该避免使用。它并非 JavaScript 核心语言的一部分，未来将可能会被移除掉。

str.indexOf(searchString[, position]) //在大于或等于position索引处的第一次出现。
str.match(regexp)//找到一个或多个正则表达式的匹配。
const paragraph = 'The quick brown fox jumps over the lazy dog. It barked.';
let regex = /[A-Z]/g;
let found = paragraph.match(regex);
console.log(found);
// Expected output: Array ["T", "I"]
regex = /[A-Z]/;
found = paragraph.match(regex);
console.log(found);
// Expected output: Array ["T"]

//match类似 indexOf() 和 lastIndexOf()，但是它返回指定的值，而不是字符串的位置。
var str = '123123000'
str.match(/\w{3}/g).join(',') // 123,123,000

str.search(regexp)//如果匹配成功，则 search() 返回正则表达式在字符串中首次匹配项的索引;否则，返回 -1
const paragraph = '? The quick';

// Any character that is not a word character or whitespace
const regex = /[^\w\s]/g;

console.log(paragraph.search(regex));
// Expected output: 0

str.repeat(count)//返回副本
str.replace(regexp|substr, newSubStr|function)//返回一个由替换值（replacement）替换部分或所有的模式（pattern）匹配项后的新字符串。
const p = 'lazy dog.Dog lazy';//如果pattern是字符串，则仅替换第一个匹配项。
console.log(p.replace('dog', 'monkey'));
// "lazy monkey.Dog lazy"

let regex = /dog/i;//如果非全局匹配，则仅替换第一个匹配项
console.log(p.replace(regex, 'ferret'));
//"lazy ferret.Dog lazy"

regex = /d|Dog/g;
console.log(p.replace(regex, 'ferret'));
//"lazy ferretog.ferret lazy"

//当使用一个 regex 时，您必须设置全局（“g”）标志， 否则，它将引发 TypeError：“必须使用全局 RegExp 调用 replaceAll”。
const p = 'lazy dog.dog lazy';//如果pattern是字符串，则仅替换第一个匹配项。
console.log(p.replaceAll('dog', 'monkey'));
// "lazy monkey.monkey lazy"

let regex = /dog/g;//如果非全局匹配，则仅替换第一个匹配项
console.log(p.replaceAll(regex, 'ferret'));
//"lazy ferret.ferret lazy"

正则表达式Regular Expression(RegExp)

RegExp 对象是一个预定义了属性和方法的正则表达式对象

字面量和字符串

//以下三种表达式都会创建相同的正则表达式：

/ab+c/i; //字面量形式      /正则表达式主体/修饰符(可选)
new RegExp('ab+c', 'i'); // 首个参数为字符串模式的构造函数
new RegExp(/ab+c/, 'i'); // 首个参数为常规字面量的构造函数

//防止在字符串中被解译成一个转义字符
var re = new RegExp("\\w+");//需要常规的字符转义规则（在前面加反斜杠 \）
var re = /\w+/;

当表达式被赋值时，字面量形式提供正则表达式的编译（compilation）状态，

当正则表达式保持为常量时使用字面量。

例如在循环中使用字面量构造一个正则表达式时，正则表达式不会在每一次迭代中都被重新编译（recompiled）。

正则表达式对象的构造函数，如

new RegExp('ab+c')

提供了正则表达式运行时编译（runtime compilation）。

如果你知道正则表达式模式为变量，如用户输入，这些情况都可以使用构造函数。

regexp.test和regexp.exec

regexp.test(str)返回Bool

regexp.exec(str)返回匹配的子串 或者 null

常用修饰符

• i ignoreCase 执行对大小写不敏感的匹配。
• g global 执行全局匹配（查找所有匹配而非在找到第一个匹配后停止）。
• y sticky 粘性匹配 从源字符串的RegExp.prototype.lastIndex位置开始匹配，

lastIndex

只有 "

g

" 或"

y

" 标志时，lastIndex才会起作用。

y

：下一次匹配一定在

lastIndex

位置开始；

g

：下一次匹配可能在

lastIndex

位置开始，也可能在这个位置的后面开始。

lastIndex

str.length，则匹配失败，

匹配失败，则

lastIndex

被设置为 0。

let str = '#foo#'
let regex = /foo/y

regex.lastIndex = 1
regex.test(str)      // true
regex.lastIndex = 5
regex.test(str)      // false (lastIndex is taken into account with sticky flag)
regex.lastIndex      // 0 (reset after match failure)

分组

‘(

正则表达式

)’

每一个分组都是一个子表达式

回溯引用

（backreference）指的是模式的后面部分引用前面已经匹配到的子字符串。

回溯引用的语法像**

\1

,

\2

**,....,其中

\1

表示引用的第一个子表达式，

\2

表示引用的第二个子表达式，以此类推。而**

\0

则表示整个表达式**。

匹配两个连续相同的单词:\b(\w+)\s\1
Hello what what is the first thing, and I am am scq000.

回溯引用在替换字符串中十分常用，语法上有些许区别，用

$1

,

$2

...来引用要被替换的字符

var str = 'abc abc 123';
str.replace(/(ab)c/g,'$1g');
// 得到结果 'abg abg 123'

匹配

选择匹配：(子模式)|(子模式)

多重选择模式：在多个子模式之间加入选择操作符。

为了避免歧义：(子模式)。

var r = /(abc)|(efg)|(123)|(456)/;

惰性匹配：最小化匹配

重复类量词都具有贪婪性，在条件允许的前提下，会匹配尽可能多的字符。

• ?、{n} 和 {n,m} 重复类具有弱贪婪性，表现为贪婪的有限性。
• *、+ 和 {n,} 重复类具有强贪婪性，表现为贪婪的无限性。

越左的重复类量词优先级越高，会在保证右侧重复类量词最低匹配次数基础上，使最左侧的重复类量词尽可能占有所有字符。

var s = "<html><head><title></title></head><body></body></html>";
var r = /(<.*>)(<.*>)/
var a = s.match(r);

console.log(a[0])//整个表达式匹配'<html><head><title></title></head><body></body></html>'
console.log(a[1]);//左侧表达式匹配"<html><head><title></title></head><body></body></html>"
console.log(a[2]);//右侧表达式匹配“</html>”

定义：在满足条件的前提下，尽可能少的匹配字符。

方法：在重复类量词后面添加问号**?**限制词。

贪婪匹配体现了最大化匹配原则，惰性匹配则体现最小化匹配原则。

var s = "<html><p><title></title></head><body></body></html>";
var r = /<.*?>/
var a = s.match(r);  //返回单个元素数组["<html>"]而不是最短的<p>

针对 6 种重复类惰性匹配的简单描述如下：

• {n,m}?：尽量匹配 n 次，但是为了满足限定条件也可能最多重复 m 次。
• {n}?：尽量匹配 n 次。
• {n,}?：尽量匹配 n 次，但是为了满足限定条件也可能匹配任意次。
• ??：尽量匹配，但是为了满足限定条件也可能最多匹配 1 次，相当于 {0,1}?。
• **+?**：尽量匹配 1 次，但是为了满足限定条件也可能匹配任意次，相当于 {1,}?。
• *? ：尽量不匹配，但是为了满足限定条件也可能匹配任意次，相当于 {0,}?。

前/后向查找：匹配括号中的内容（不包含括号）

包括括号：[\S+?]

不包括括号：(?<=[)\S+?(?=])

后向查找：**(?<=exp)是以exp开头的字符串, 但不包含本身**.

负后向查找：**(?<!exp) ，被指定的子表达式不能被匹配到**。

前向查找：**(?=exp)就匹配为exp结尾的字符串, 但不包含本身**.

负前向查找:：**(?!exp),被指定的子表达式不能被匹配到**。

\S 匹配任何非空白字符。等价于[^\f\n\r\t\v]。

如果不支持后向查找：将字符串进行翻转，然后再使用前向查找，作完处理后再翻转回来

技巧

反义字符

可以匹配很多无法直接描述的字符，达到以少应多的目的。

var r = /[^0123456789]/g;

边界量词

边界就是确定匹配模式的位置，如字符串的头部或尾部，具体说明如表所示。

JavaScript 正则表达式支持的边界量词
量词说明^匹配开头，在多行检测中，会匹配一行的开头$匹配结尾，在多行检测中，会匹配一行的结尾

1. var s = "how are you"

1. 匹配最后一个单词

var r = /\w+$/;
var a = s.match(r); //返回数组["you"]

1. 匹配第一个单词

var r = /^\w+/;
var a = s.match(r); //返回数组["how"]

1. 匹配每一个单词

var r = /\w+/g;
var a = s.match(r); //返回数组["how","are","you"]

应用

str.split()

使用正则来划分带有多种行结束符和换行符的文本

//对于不同的平台（Unix，Windows 等等），其默认的行结束符是不一样的。而下面的划分方式适用于所有平台。
let text = 'Some text\nAnd some more\r\nAnd yet\rThis is the end'
let lines = text.split(/\r\n|\r|\n/)
console.log(lines) // logs [ 'Some text', 'And some more', 'And yet', 'This is the end' ]

str.match()

在字符范围内可以混用各种字符模式。

var s = "abcdez";  //字符串直接量
var r = /[abce-z]/g;  //字符a、b、c，以及从e~z之间的任意字符
var a = s.match(r);  //返回数组["a","b","c","e","z"]

str.match(regexp)//找到一个或多个正则表达式的匹配。
const paragraph = 'The quick brown fox jumps over the lazy dog. It barked.';
let regex = /[A-Z]/g;
let found = paragraph.match(regex);
console.log(found);
// Expected output: Array ["T", "I"]
regex = /[A-Z]/;
found = paragraph.match(regex);
console.log(found);
// Expected output: Array ["T"]

//match类似 indexOf() 和 lastIndexOf()，但是它返回指定的值，而不是字符串的位置。
var str = '123123000'
str.match(/\w{3}/g).join(',') // 123,123,000

str.replace()

使用正则改变数据结构

let re = /(\w+)\s(\w+)/;//匹配姓名 first last 输出新的格式 last, first。
let str = "John Smith";
let newstr = str.replace(re, "$2, $1");//$1 和 $2 指明括号里先前的匹配
console.log(newstr);//"Smith, John".

str.replace(regexp|substr, newSubStr|function)//返回一个由替换值（replacement）替换部分或所有的模式（pattern）匹配项后的新字符串。
const p = 'lazy dog.Dog lazy';//如果pattern是字符串，则仅替换第一个匹配项。
console.log(p.replace('dog', 'monkey'));
// "lazy monkey.Dog lazy"

let regex = /dog/i;//如果非全局匹配，则仅替换第一个匹配项
console.log(p.replace(regex, 'ferret'));
//"lazy ferret.Dog lazy"

regex = /d|Dog/g;
console.log(p.replace(regex, 'ferret'));
//"lazy ferretog.ferret lazy"

//当使用一个 regex 时，您必须设置全局（“g”）标志， 否则，它将引发 TypeError：“必须使用全局 RegExp 调用 replaceAll”。
const p = 'lazy dog.dog lazy';//如果pattern是字符串，则仅替换第一个匹配项。
console.log(p.replaceAll('dog', 'monkey'));
// "lazy monkey.monkey lazy"

let regex = /dog/g;//如果非全局匹配，则仅替换第一个匹配项
console.log(p.replaceAll(regex, 'ferret'));
//"lazy ferret.ferret lazy"

设计对提交的表单字符串进行敏感词过滤。先设计一个敏感词列表，然后使用竖线把它们连接在一起，定义选择匹配模式，最后使用字符串的 replace() 方法把所有敏感字符替换为可以显示的编码格式。

var s = '<meta charset="utf-8">';  //待过滤的表单提交信息
var r = /\'|\"|\<|\>/gi;  //过滤敏感字符的正则表达式
function f() {  //替换函数
    把敏感字符替换为对应的网页显示的编码格式
    return "&#" + arguments[0].charCodeAt(0) + ";";
}
var a =s.replace(r,f);  //执行过滤替换 
document.write(a);  //在网页中显示正常的字符信息
console.log(a);

str.serach()

str.search(regexp)//如果匹配成功，则 search() 返回正则表达式在字符串中首次匹配项的索引;否则，返回 -1
const paragraph = '? The quick';

// Any character that is not a word character or whitespace
const regex = /[^\w\s]/g;

console.log(paragraph.search(regex));
// Expected output: 0

合法的URL

URL结构一般包括协议、主机名、主机端口、路径、请求信息、哈希

1. 首先必须是以http(s)开头并且可以不包含协议头部信息
2. 主机名可以使用"-"符号，所以两种情况都要判断，包含"-"或不包含"-"
3. 顶级域名很多，直接判断"."之后是否为字母即可
4. 最后判断端口、路径和哈希，这些参数可有可无

 域名中只能包含以下字符
  1. 26个英文字母
  2. "0，1，2，3，4，5，6，7，8，9"十个数字
  3. "-"(英文中的连词号，但不能是第一个字符)

https://www.bilibili.com/video/BV1F54y1N74E/?spm_id_from=333.337.search-card.all.click&vd_source=6fd32175adc98c97cd87300d3aed81ea
//开始:                     ^
//协议:                     http(s)?:\/\/
//域名:                     [A-z0-9]+-[A-z0-9]+|[A-z0-9]+
//顶级域名 如com cn,2-6位:   [a-zA-Z]{2,6}
//端口 数字:                (\d+)?
//路径 任意字符 如 /login:   (\/.+)?
//哈希 ? 和 # ，如?age=1:    (\?.+)?(#.+)?
//结束:                      $
//     https://           www.bilibili                com    /video/BV1F54y1N74E  ?spm..            
/^(http(s)?:\/\/)?(([a-zA-Z0-9]+-[a-zA-Z0-9]+|[a-zA-Z0-9]+)\.)+([a-zA-Z]{2,6})(:\d+)?(\/.+)?(\?.+)?(#.+)?$/.test(url)

常用字符

\标记下一个字符是特殊字符或文字。例如，"n”和字符"n”匹配。"\n"则和换行字符匹配。

^匹配输入的开头.
$匹配输入的末尾

·匹配除换行字符外的任何单个字符
匹配前一个字符零或多次。例如，"zo”与"z”或"zoo”匹配。
+匹配前一个字符一次或多次。例如，"zo+"与"zoo”匹配，但和"z”不匹配。
?匹配前一个字符零或一次。例如，"a?ve?”和"never"中的“"ve”匹配。
x|y 匹配x或y
{n}匹配n次。n是非负整数
{n,} n是一个非负整数。至少匹配n次。例如，"o{2,)"和"Bob”中的"o”不匹配，但和"foooood"中的所有o匹配。"o{1}”与"o+”等效。"o{0,}”和"o*”等效。
{n,m}m和n是非负整数。至少匹配n次而至多匹配 m次。例如，"o{1,3]"和"fooooood”中的前三个o匹配。"o{0,1}”和“o?”等效。
[xyz]匹配括号内的任一字符。例如，"[abc]"和"plain”中的"a”匹配。

[^xyz]匹配非括号内的任何字符。例如，"[^abc]"和“plain”中的"p”匹配。
[a-z]字符范围。和指定范围内的任一字符匹配。例如，"[a-z]”匹配"a"到"z"范围内的任一小写的字母表字符。

[^m-z]否定字符范围。匹配不在指定范围内的任何字符。例如，"[m-z]”匹配不在"m"到"z"范围内的任何字符。

助记：digital

\d匹配数字字符。等价于[0-9]。
\D匹配非数字字符。等价于[^0-9]。

助记：space

\s匹配任何空白，包括空格、制表、换页等。与"[ \fn\rlt\v]”等效。
\S匹配任何非空白字符。与"[^ \fn\rlt\v]”等效。

\w匹配包括下划线在内的任何字字符。与"**[A-Za-z0-9_]**”等效。

\W匹配任何非字字符。与"[^A-Za-z0-9_]”等效。

元字符表

元字符描述.查找单个字符，除了换行和行结束符\w查找单词字符\W查找非单词字符\d查找数字\D查找非数字字符\s查找空白字符\S查找非空白字符\b匹配单词边界\B匹配非单词边界\0查找 NUL字符\n查找换行符\f查找换页符\r查找回车符\t查找制表符\v查找垂直制表符\xxx查找以八进制数 xxxx 规定的字符\xdd查找以十六进制数 dd 规定的字符\uxxxx查找以十六进制 xxxx规定的 Unicode 字符

[A-z]和[a-zA-Z]

[A-z]

将在范围匹配的ASCII字符从

A

到

z

，

[a-zA-Z]

将在范围中的范围匹配的ASCII字符从

A

到

Z

和从

a

到

z

。

查看ASCII字符的this table，则会看到

A-z

包含

[

,

\

,

]

,

^

,

_，

## 规范

## *命名规范

建议养成每句后加;的好习惯

1. Pascal Case 大驼峰式命名法：首字母大写。eg：StudentInfo、UserInfo、ProductInfo
2. Camel Case 小驼峰式命名法：首字母小写。eg：studentInfo、userInfo、productInfo

### 常量

命名方法：名词全部大写
 命名规范：使用大写字母和下划线来组合命名，下划线用来分割单词

const MAX_COUNT = 10;

### 变量，函数

命名方法: 小驼峰式命名法
 命名规范：前缀为形容词（变量） ，前缀为动词（函数）

let maxCount = 10;

/**

*

• @param n int整型 the n
• @return int整型

*/
function setConut(n){
this.count=n;
return n
}

### 类

类 & 构造函数

命名方法：大驼峰式命名法，首字母大写。

命名规范：前缀为名称。


- 公共属性和方法：跟变量和函数的命名一样。
- 私有属性和方法：前缀为_(下划线)，后面跟公共属性和方法一样的命名方式。

class Person {
private _name: string;
constructor() { }
// 公共方法
getName() {
return this._name;
}
// 公共方法
setName(name) {
this._name = name;
}
}
const person = new Person();
person.setName('mervyn');
person.getName(); // ->mervyn

## *注释

### HTML

<!-- 注释 -->

### CSS

p{
color: #ff7000; /字体颜色设置/
height：30px; /段落高度设置/
}

```

/注释/

JS

//注释

/注释/

leetcode刷题攻略

基础笔试套路