正态分布是高斯概率分布。高斯概率分布是反映中心极限定理原理的函数,该定理指出当随机样本足够大时,总体样本将趋向于期望值并且远离期望值的值将不太频繁地出现。高斯积分是高斯函数在整条实数线上的定积分。这三个主题,高斯函数、高斯积分和高斯概率分布是这样交织在一起的,所以我认为最好尝试一次性解决这三个主题(但是我错了,这是本篇文章的不同主题)。本篇文章我们首先将研究高斯函数的一般定义是什么,然后将看一下高斯积分,其结果对于确定正态分布的归一化常数是非常必要的。最后我们将使用收集的信息理解,推导出正态分布方程。
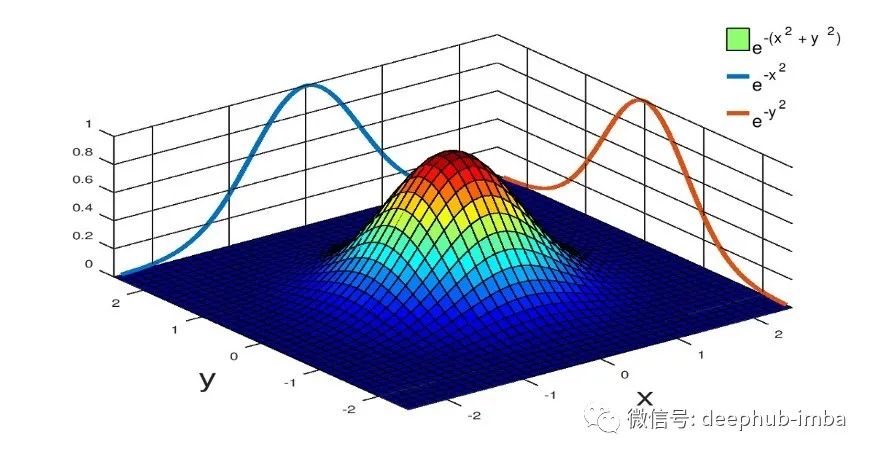
首先,让我们了解高斯函数实际上是什么。高斯函数是将指数函数 exp(x) 与凹二次函数(例如 -(ax^2+bx+c) 或 -(ax^2+bx) 或只是-ax^2组成的函数。结果是一系列呈现“钟形曲线”的形状的函数。

两个高斯函数的图。第一个高斯(绿色)的λ=1和a=1。第二个(橙色)λ=2和a=1.5。两个函数都不是标准化的。也就是说,曲线下的面积不等于1。
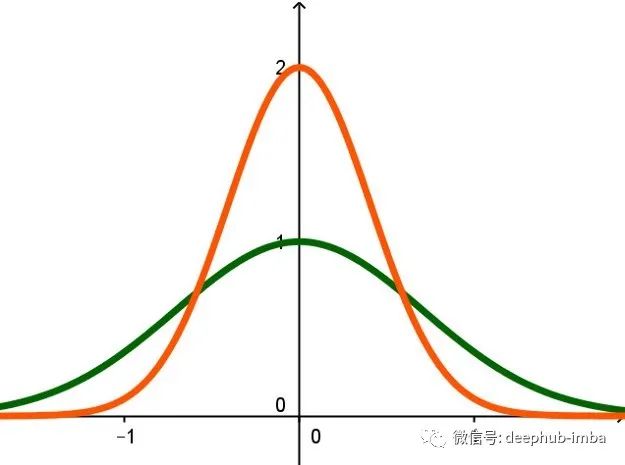
大多数人都熟悉这类曲线是因为它们在概率和统计中被广泛使用,尤其是作为正态分布随机变量的概率密度函数。在这些情况下,函数具有的系数和参数既可以缩放“钟形”的振幅,改变其标准差(宽度),又可以平移平均值,所有这一切都是在曲线下的面积进行归一化(缩放钟形,使曲线下的面积总是等于1)的同时进行的。结果是一个高斯函数包含了一大堆的参数来影响这些结果。
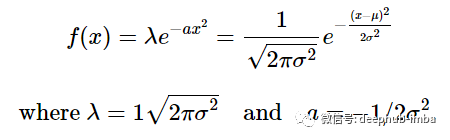
如果将其认为是均值 = μ 且标准差 = σ 的正态分布方程。将其与高斯 λ exp(-ax^2) 的一般形式进行比较,我们可以看到:
- (x - μ)^2表示的是均值μ如何在x轴上左右平移图像,这就是均值要做的。如果μ=0,那么图的中心为0。
- σ^2,是一个测量随机变量的方差,也就是说数据是如何分散的,当我们使用a=1/(2σ^2)缩小或扩大图形时,我们希望同时缩放图形使用λ=1/√2πσ^2。这样图下的面积才能保持为1。
前导系数 λ 有时表示为 1/Z,其中 Z=√2πσ^2,正是这样的一个结果将我们带到了本文的主要观点之一:√2πσ^2有时被称为一个自变量的正态分布的归一化常数,而1/√2πσ2则被称为归一化常数。在这两种情况下,公式中都有 π,它是从哪里来的?它通常与圆、径向对称和/或极坐标相关联。单个变量的函数如何以 π 作为其在前导系数中的归一化参数之一呢?
可以参考我们以前的文章,里面有非常详细的描述
高斯积分
不定积分 ∫ exp(x^2) dx 不可能用初等函数求解。有没有任何积分方法可以用来求解不定积分?

可以计算定积分,如上所述,首先对高斯函数求平方从而在 x 和 y 中产生一个具有径向对称二维图的两个变量函数。这样能够将直角坐标系转换为极坐标,在此基础上就可以使用更熟悉的积分方法(例如置换)进行积分。然后,简单地取结果的平方根(因为我们在开始时对积分进行平方) 就得到了我们的答案,顺便说一句,结果是是√π。
对高斯积分求平方

方法的第一步是对积分求平方——也就是说,我们将一维转换为二维,这样就可以使用多变量微积分的技术来求解积分

可以重写为:

这两个积分用x和y表示是等价的;所以它等同于x的单个积分的平方。因为变量x和y是独立的,所以可以把它们移进或移出第二个积分符号,可以这样写:
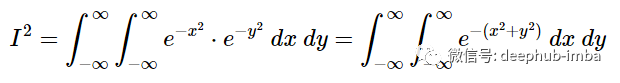
如果你不熟悉如何解二重积分也不用担心。只需先使用内部变量进行积分得到单个积分。然后用左边的变量和外面的变量积分。但现在还不需要这么做。这里需要注意的是当我们对积分进行平方时,得到了一个二维的图形化的径向对称的高斯函数。用x和y来表示积分e的指数是- (x^2+y^2)给了我们下一步应该做什么的线索。
转换为极坐标
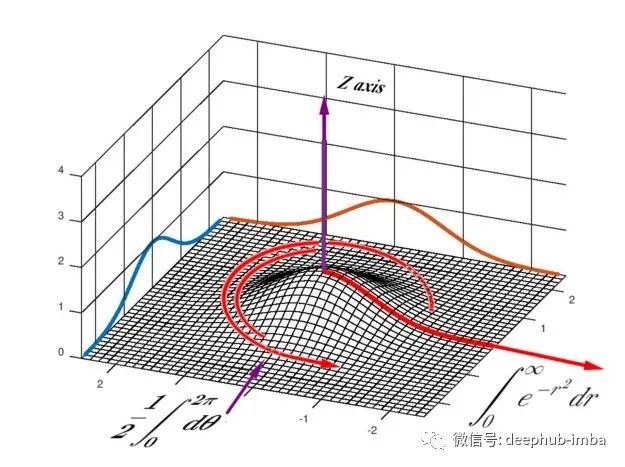
这里棘手的部分是,我们必须将直角坐标下的二重积分转换成极坐标下的二重积分。
为了在极坐标中对整个无限区域进行积分,我们首先对 exp(−r²) 相对于从 x=0 开始并延伸到无穷大的半径 r 进行积分。结果是一个无限薄的楔形,看起来像我们原始一维高斯曲线的一半。然后我们围绕旋转轴 Z 轴旋转楔形,并累积无限数量的这些极薄的楔形。也就是说——我们在 π 从 0 到 2π 时积分。
我们现在的二重积分看起来像这样:

我们可以用 r^2 替换指数中的 −(x^2+y^2),这要感谢毕达哥拉斯。但是我们仍然需要将我们的微分从矩形转换为极坐标。
微分的转换简单的表示如下:

在任何情况下,我们的二重积分现在看起来像这样:

添加适当的积分边界:
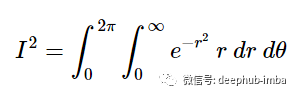
如果我们设u=r^2,那么du=2r,我们可以写成(对于内积分)

然后求出外积分:
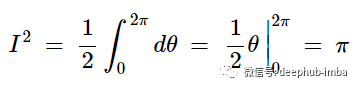
所以:

我们在下一节求解标准化常数时,这个结果很重要。
正态分布函数的推导
现在我们有了推导正态分布函数的所有前提。下面将分两步来做:首先确定我们需要的概率密度函数。这意味着以λ为单位重新转换-a-产生的函数,无论为λ选择什么值,曲线下的面积总是1。然后用随机变量的方差σ^2来转换λ。对整个实数线上的方差进行积分 从而得到我们在前导系数 √2πσ^2 中需要归一化常数的项,也是我们在分母中需要的项指数 2σ^2。我们将使用分部积分来求解方差积分。
概率密度函数的推导
我们将从广义高斯函数f(x)=λ exp(−ax^2)开始,正态分布下的面积必须等于1所以我们首先设置广义高斯函数的值,对整个实数线积分等于1

这里将 -a- 替换为 a^2 稍微修改了高斯分布。为什么要这样做?因为它可以使用 换元积分 U-substitution 来解决这个积分。为什么我们可以这样做?因为 -a- 是一个任意常数,所以a^2 也只是一个任意常数,可以使用 U-substitution 求解。让 u=ax 和 du=a dx 这意味着 dx=du/a, 由于 λ 和 1/a 是常数,我们可以将它们移到积分符号之外,得到:
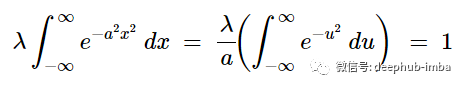
我们从上面关于高斯积分的讨论中知道,右边积分的值等于√π。这样就可以改成:
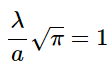
求解 -a- 可以这样写:
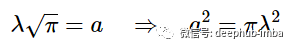
根据已经发现的λ 和 -a- 之间的关系,修改后的高斯下的面积总是等于 1 也是必须的,所以我们可以进一步修改,用 πλ^2 代替 a^2 并写:

无论 λ 的值如何,该曲线下的面积始终为 1。这是我们的概率密度函数。
确定归一化常数
在获得归一化概率分布函数之前还需要做一件事:必须将 λ 重写为随机变量方差 σ^2 的函数。这将涉及对整个实数线的方差表达式进行积分所以需要采用按分部积分来完成此操作。
如果给定一个概率密度函数 f(x) 和一个均值 μ,则方差定义为从均值平方(x - μ)^2的偏差乘以整个实数线的概率密度函数f(x)的积分:

假设μ=0,因为已经有了概率密度函数h(x),所以可以写成
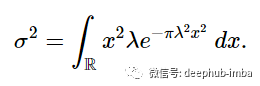
用分部积分法求解这个积分有:
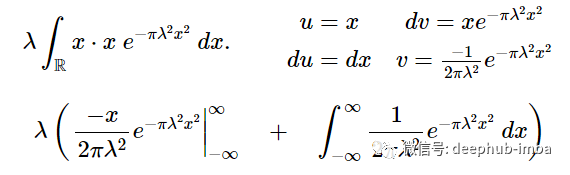
第一项归零是因为指数中的x^2项比前一项分子中的- x项趋近于∞的速度快得多所以我们得到
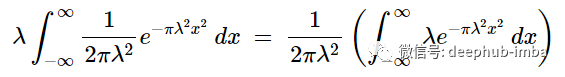
右边的被积函数是概率密度函数,已经知道当对整个实数线进行积分时它的值是1 :
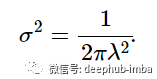
求解 λ 得到:
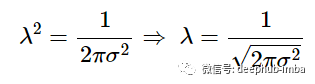
将 λ 的 1/√2πσ^2 代入我们的修改后的公式(即我们的概率密度函数),我们得到:
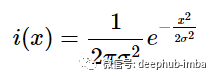
剩下要做的就是将平均值 μ 放入指数的分子中,以便可以根据 μ 的值沿 x 轴平移图形:
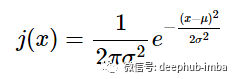
这样就完成了方程推导
作者 :Manin Bocss