数据结构 六 理解二叉搜索树的实现

数据结构就是定义出某种结构：像数组结构、链表结构、树形结构等，实现数据结构就是我们主动去管理增删查改的实现函数

二叉搜索树的概念

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树

非空左子树上所有节点的值都小于根节点的值，右子树上所有节点的值都大于根节点的值

二叉搜索树的定义

template<class K>//搜索二叉树
struct BSTreeNode
{
  BSTreeNode<K>* _left;//左孩子指针
  BSTreeNode<K>* _right;//右孩子指针
  K _key;//节点数据值
  //构造函数
  BSTreeNode(const K& key):_left(nullptr),_right(nullptr),_key(key)
  {}
};

先来了解一下文件BinnarySearchTree.h中的接口

template<class K>
class BSTree
{
    typedef BSTreeNode<K> Node;    //重命名上面的定义 
public
    //递归查找
    bool FindR(const K& key)
    {
        return _FindR(_root, key);
    }
    //递归插入
    bool InsertR(const K& key)
    {
        return _InsertR(_root, key);
    }
    //递归删除
    bool EraseR(const K& key)
    {
        return _EraseR(_root, key);
    }
    //中序遍历 类内调用拿root
    void InOrder()
    {
        _InOrder(_root);
        cout << endl;
    }

    //构造函数
    BSTree() = default;
    //拷贝构造
    BSTree(const BSTree<K>& t)；
    //赋值函数
    BSTree<K>& operator=(BSTree<K> t)；
    //析构函数
    ~BSTree()；
private:
    //类部子函数不继承的话通常私有
    bool _EraseR(Node*& root,const K& key)；//递归删除
    bool _InsertR(Node*& root,const K& key)；//递归插入
    bool _FindR(Node* root,const K& key)；//递归查找
    void _InOrder(Node* root)；//中序遍历函数
    void DestroyTree(Node* root)//置空函数
    Node* CopyTree(Node* root)//树的拷贝
private:
    Node* _root = nullptr;
};

下面我们来详细学习函数接口的具体实现

递归插入函数的定义

//递归插入函数
bool _InsertR(Node*& root,const K& key)//递归插入
{
  if (root == nullptr)//为空就申请节点插入数据
  {
    root = new Node(key);//注意上面传指针引用 可以直接连接 
    return true;
  }
  if (key > root->_key)//插入的值大于根 往右走
  {
    return _InsertR(root->_right, key);
  }
  else if (key < root->_key)//插入的值小于根 往右走
  {
    return _InsertR(root->_left, key);
  }
  else
  {
    return false;//相等说明数据已经有了
  }
}

递归删除函数的定义

bool _EraseR(Node*& root,const K& key)//递归删除
{
  //先找到要删除的节点
  if (root == nullptr)//为空返回false
  {
    return false;
  }
  if (key > root->_key)//要删除的大于根
  {
    return  _EraseR(root->_right, key);//递归右树找
  }
  else if (key < root->_key)//要删除的小于根
  {
    return  _EraseR(root->_left, key);//递归左树找
  }
  
  //走到这里说明已经找到要删除的数据
  else
  {
    //1.删除一个孩子 左为空或右为空 托孤   
  
    Node* del = root;//先保存要删除的节点
    if (root->_left == nullptr)//左为空 让父亲指向右
    {
      root = root->_right;//引用
    }
    else if (root->_right == nullptr)右为空 让父亲指向左
    {
      root = root->_left;
    }
    
    //2.删除2个孩子左右都不为空 替换法
    else
    {
      Node* minRight = root->_right;//
      while (minRight->_left)
      {
        minRight = minRight->_left;
      }
      swap(root->_key, minRight->_key);//交换数据
      //此时要删除的已经换下来 再去右树递归删除
      return _EraseR(root->_right, key);//指定树    
    }
    delete del;
    return true;
  }
}

中序遍历函数的定义

//中序遍历
void _InOrder(Node* root) 左子树 根 右子树
{
  if (root == nullptr)
      return;
  _InOrder(root->_left);//先走左边
  cout << root->_key << " "; 打印数据
  _InOrder(root->_right);//后走右边
}

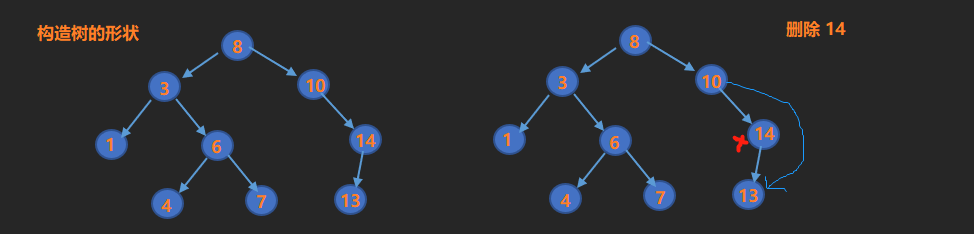
我们先用以上接口实现图中二叉树的插入和删除测试案例TestBSTree

//递归插入测试
void TestBSTree1()
{
  //
  BSTree<int> t;
  int a[] = { 8,3,1,10,6,4,7,14,13, };
  for (auto e : a)
  {
    t.InsertR(e);//依次插入 默认去重 
  }
  t.InOrder();//遍历打印 1 3 4 6 7 8 10 13 14
}

//递归删除测试
void TestBSTree2()
{
  //
  BSTree<int> t;
  int a[] = { 8,3,1,10,6,4,7,14,13, };
  for (auto e : a)
  {
    t.InsertR(e);//依次插入 默认去重 
  }
  t.InOrder();//打印1 3 4 6 7 8 10 13 14

  t.EraseR(14);//删除14
  t.InOrder();//打印1 3 4 6 7 8 10 13
}
int main()
{
  TestBSTree1();//递归插入
  TestBSTree2();//递归删除
  return 0;
}

递归查找函数的定义

从根开始比较查找，比根大则往右边查找，比根小则往左边查找

bool _FindR(Node* root,const K& key)//递归查找
{

  if (root == nullptr)
    return false;
  if (key > root->_key)//
  {
    return _FindR(root->_right, key);
  }
  else if(key < root->_key)
  {
    return _FindR(root->_left, key);
  }
  else
  {
    return true;//相等就找到了
  }
}

置空函数定义

置空函数一般会放在我们进行插入或删除的函数最后，释放我们在堆上申请的空间，将其还给操作系统，另外也会相应的进行检查越界等问题

void DestroyTree(Node* root)//置空函数
{
  if (root == nullptr)
    return;
  DestroyTree(root->_left);
  DestroyTree(root->_right);
  delete root;
}

析构函数定义

~BSTree()//析构函数
{
  DestroyTree(_root);//调用置空函数
  _root = nullptr;
}

赋值函数定义

BSTree<K>& operator=(BSTree<K> t)//赋值函数
{
  swap(_root, t._root);
  return *this;
}

树的拷贝函数定义

Node* CopyTree(Node* root)//拷贝树
{
  if (root == nullptr)
    return nullptr;
  Node* copynode = new Node(root->_key);
  copynode->_left = CopyTree(root->_left);//递归创建左树
  copynode->_right = CopyTree(root->_right);//递归创建右树
  return copynode;
}

拷贝构造函数定义

BSTree(const BSTree<K>& t)//拷贝构造
{
  _root = CopyTree(t._root);//调用下方树的拷贝函数
  cout << "调用拷贝构造" << endl;
}

我们再用上面这几个接口实现第3个测试案例TestBSTree3

//赋值函数测试
void TestBSTree3()
{
  //
  BSTree<int> t;
  int a[] = { 8,3,1,10,6,4,7,14,13, };
  for (auto e : a)
  {
    t.InsertR(e);//依次插入 默认去重 
  }
  t.InOrder();//遍历打印 1 3 4 6 7 8 10 13 14
  BSTree<int> t1;
  t1 = t;//赋值函数 调用拷贝构造
  t.InOrder();//遍历打印1 3 4 6 7 8 10 13 14
}

int main()
{
  TestBSTree3();//赋值函数测试
  return 0;
}

最后这里放一下整个二叉搜索树递归版本代码的实现，方便大家观察理解

#pragma once
template<class K>//搜索二叉树
struct BSTreeNode
{
  BSTreeNode<K>* _left;
  BSTreeNode<K>* _right;
  K _key;
  //构造函数
  BSTreeNode(const K& key):_left(nullptr),_right(nullptr),_key(key)
  {}
};

template<class K>
class BSTree
{
  typedef BSTreeNode<K> Node;

public:

    //默认构造
    BSTree() = default;
    //拷贝构造
    BSTree(const BSTree<K>& t)
    {
        _root = CopyTree(t._root);
        cout << "调用拷贝构造" << endl;
    }
    //赋值函数
    BSTree<K>& operator=(BSTree<K> t)
    {
        swap(_root, t._root);
        return *this;
    }
    //析构函数
    ~BSTree()
    {
        DestroyTree(_root);
        _root = nullptr;
    }
    //递归查找
    bool FindR(const K& key)
    {
        return _FindR(_root, key);
    }
    //递归插入
    bool InsertR(const K& key)
    {
        return _InsertR(_root, key);
    }
    //递归删除
    bool EraseR(const K& key)
    {
        return _EraseR(_root, key);
    }
    //中序遍历 类内调用拿root
    void InOrder()
    {
        _InOrder(_root);
        cout << endl;
    }
private://类部子函数不继承的话通常私有
    //递归删除
    bool _EraseR(Node*& root,const K& key)
    {
        if (root == nullptr)
        {
            return false;
        }
        if (key > root->_key)//
        {
            return  _EraseR(root->_right, key);
        }
        else if (key < root->_key)
        {
            return  _EraseR(root->_left, key);
        }
        else
        {
            Node* del = root;//保存要删除的节点
            //相等说明可以删除了 三种情况
            if (root->_left == nullptr)
            {
                root = root->_right;//引用
            }
            else if (root->_right == nullptr)
            {
                root = root->_left;
            }
            else//左右都不为空 替换法
            {
                Node* minRight = root->_right;
                while (minRight->_left)
                {
                    minRight = minRight->_left;
                }
                swap(root->_key, minRight->_key);//交换数据
                //此时要删除的已经换下来 再去右树递归删除
                return _EraseR(root->_right, key);//指定树
                
            }
            delete del;
            return true;
        }
    }

    bool _InsertR(Node*& root,const K& key)//递归插入
    {
        if (root == nullptr)//为空就申请节点插入数据
        {
            root = new Node(key);//注意上面传指针引用 可以直接连接 
            return true;
        }
        if (key > root->_key)//插入的值大于根 往右走
        {
            return _InsertR(root->_right, key);
        }
        else if (key < root->_key)//插入的值小于根 往右走
        {
            return _InsertR(root->_left, key);
        }
        else
        {
            return false;//相等说明数据已经有了
        }
    }

    bool _FindR(Node* root,const K& key)//递归查找
    {
        //
        if (root == nullptr)
            return false;
        if (key > root->_key)//
        {
            return _FindR(root->_right, key);
        }
        else if(key < root->_key)
        {
            return _FindR(root->_left, key);
        }
        else
        {
            return true;//相等就找到了
        }
    }
    void _InOrder(Node* root)//中序遍历
    {
        if (root == nullptr)
            return;

        _InOrder(root->_left);
        cout << root->_key << " ";
        _InOrder(root->_right);
    }

    void DestroyTree(Node* root)//置空函数
    {
        if (root == nullptr)
            return;
        DestroyTree(root->_left);
        DestroyTree(root->_right);
        delete root;
    }
    Node* CopyTree(Node* root)//拷贝树
    {
        if (root == nullptr)
            return nullptr;
        Node* copynode = new Node(root->_key);
        copynode->_left = CopyTree(root->_left);//递归创建左树
        copynode->_right = CopyTree(root->_right);//递归创建右树
        return copynode;
    }
private:
    Node* _root = nullptr;
};

//递归插入测试
void TestBSTree1()
{
    BSTree<int> t;
    int a[] = { 8,3,1,10,6,4,7,14,13, };
    for (auto e : a)
    {
        t.InsertR(e);//依次插入 默认去重 
    }
    t.InOrder();//遍历  
}

//递归删除测试
void TestBSTree2()
{
    BSTree<int> t;
    int a[] = { 8,3,1,10,6,4,7,14,13, };
    for (auto e : a)
    {
        t.InsertR(e);//依次插入 默认去重 
    }
    t.InOrder();//打印 1 3 4 6 7 8 10 13 14

    t.EraseR(8);//删除8
    t.EraseR(3);//删除3
    t.InOrder();//打印 1 4 6 7 10 13 14
}

//赋值函数测试
void TestBSTree3()
{
    BSTree<int> t;
    int a[] = { 8,3,1,10,6,4,7,14,13, };
    for (auto e : a)
    {
        t.InsertR(e);//依次插入 默认去重 
    }
    t.InOrder();//遍历打印 1 3 4 6 7 8 10 13 14
    BSTree<int> t1;
    t1 = t;//赋值函数 调用拷贝构造
    t.InOrder();//遍历打印1 3 4 6 7 8 10 13 14
}

int main()
{
    TestBSTree1();//插入函数测试
    TestBSTree2();//删除函数测试
    TestBSTree3();//赋值函数测试
    return 0;
}

在Java和C++的学习当中，前期学习数据结构当中的顺序表、链表、二叉树等便于我们后面更好的学习容器，后面会继续分享红黑树和排序的实现

希望这篇文章大家有所收获，我们下篇见