本篇文章将实现AlphaZero的核心搜索算法:蒙特卡洛树搜索
蒙特卡洛树搜索(MCTS)
你可能熟悉术语蒙特卡洛[1],这是一类算法,反复进行随机抽样以获得某个结果。
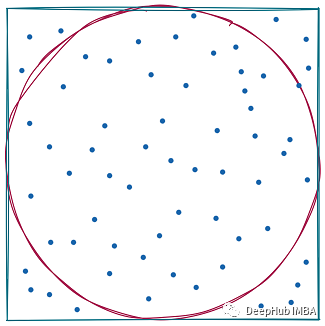
例如上图,在单位正方形中选择随机点,计算圆内有多少个点,可以用来估计pi/4的值
本文中我们将详细介绍MCTS的所有步骤。但首先我们从更广泛的理解层面来说,在游戏的MCTS中,我们从给定的棋盘状态开始重复模拟玩法,一般情况下的MCTS我们会一直执行这些模拟直到游戏结束。但AlphaZero的[2]MCTS实现与传统的MCTS不同,因为在AlphaZero中我们也有一个神经网络,它正在接受训练,为给定的板子状态提供策略和值。
AlphaZero中搜索算法的输入是一个棋盘的状态(比如σ)和我们想要运行MCTS的迭代次数(也称为播放次数)。在这个游戏的例子中,搜索算法的输出是从σ中抽样一个执行动作的策略。
该树将迭代构建。树的每个节点都包含一个棋盘状态和关于在该状态下可能采取的有效操作的信息。
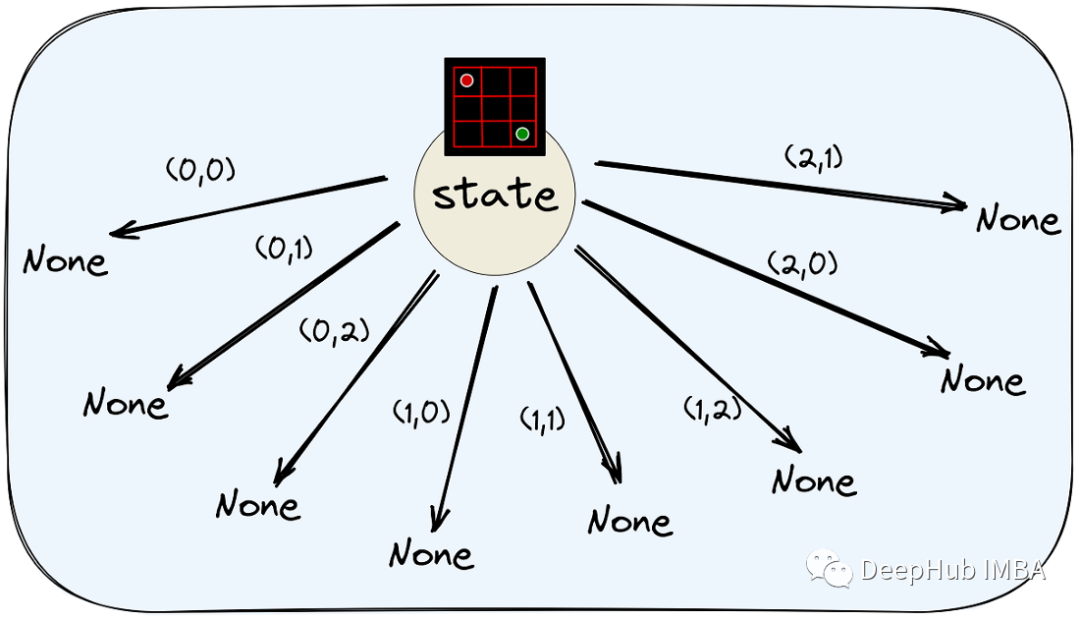
节点由一个状态板和键-值对组成,其中键是一个动作元组,对应的值是在父节点的状态上应用该动作元组后获得的节点。子节点是惰性初始化的(即仅在需要时初始化)
一开始,树只有根节点。它将包含输入状态σ和在σ下可以采取的有效动作。
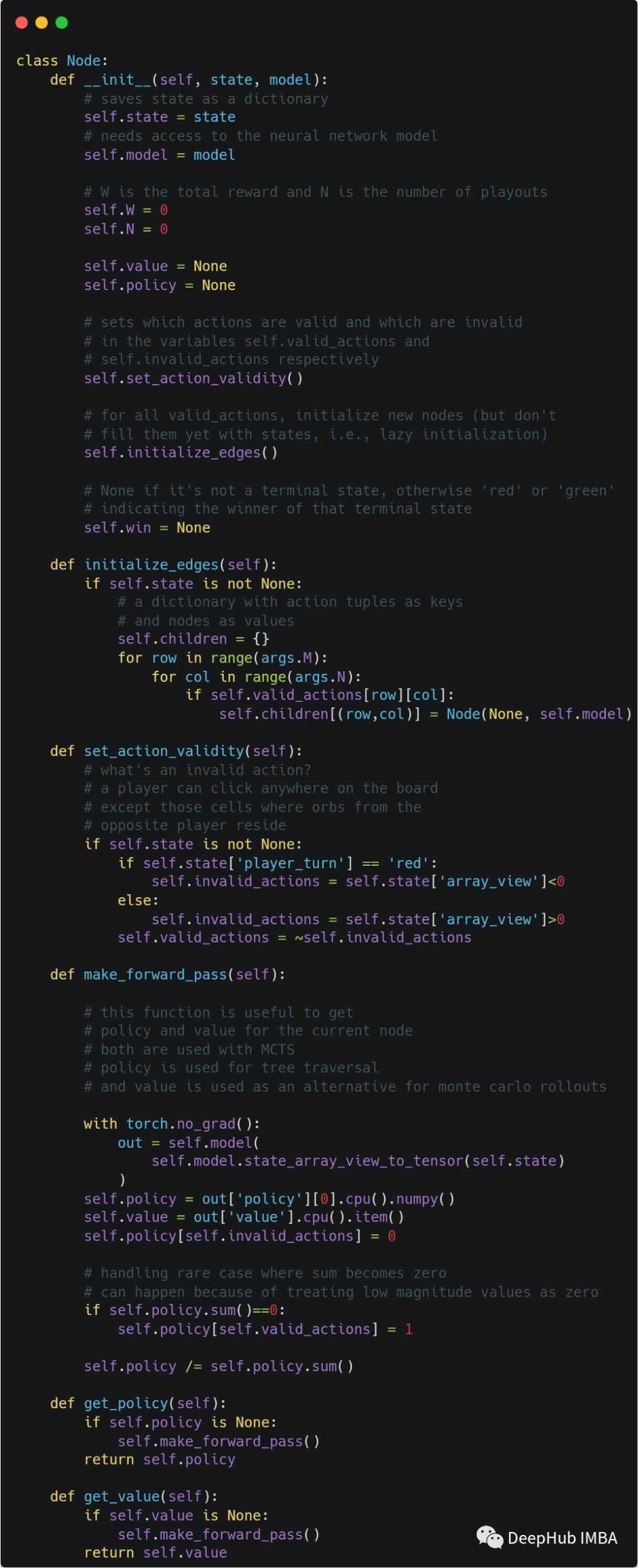
下面是Node类的代码。
MCTS的每一次模拟分为4个步骤:选择(selection)、展开expansion)、求值(evaluation)和回溯(backup),下面我们详细进行说明
选择
MCTS算法的第一步是选择。从根节点开始选择最佳边,直到到达树的末端(表示游戏结束的终端节点/尚未探索的节点,例如上图中标记为None的节点)。
但“最佳边”是什么意思呢?应该如何遍历树?如何做到树遍历的方式是在探索和使用之间取得平衡呢?(这里的探索也是神经网络主导的)
首先解释下这里的探索(exploration)和使用(exploitation)的含义:
想象一下:你从来没有吃过豆腐脑,你也不知道甜的还是咸的好吃(比如对于北方人来说可能都没听有甜的豆腐脑)。所以只能自己尝试,假设吃了一个甜的感觉很好。但当你听到还有咸的的时候,因为还没有尝试过,肯定想尝试下,这样找到一个新的口味,这个就是探索。但是如果假设你一天只能吃一种口味的,而你更新换甜味的,想吃甜的,这就是使用。
简单总结下:选择的行动的目标都是能够获得积极奖励的,但是如果行动已经了解,这就是使用;行动是找到一些能给你带来更好奖励的行动(以前没有的),这就是探索。但是因为一次只能进行一个动作,所以就需要在两者之间取得良好的平衡。
AlphaZero使用PUCT(应用于树的预测器置信上限)规则来实现这种平衡。该规则是根据经验设计的,也是受到Rosin’s work in a bandits-with-predictors setting[3]的工作的推动。DeepMind最近的一篇论文[4]讨论了PUCT的一些替代方案。我们将在后面关于未来方向的部分中讨论这些替代方案。我们先试着理解PUCT规则。
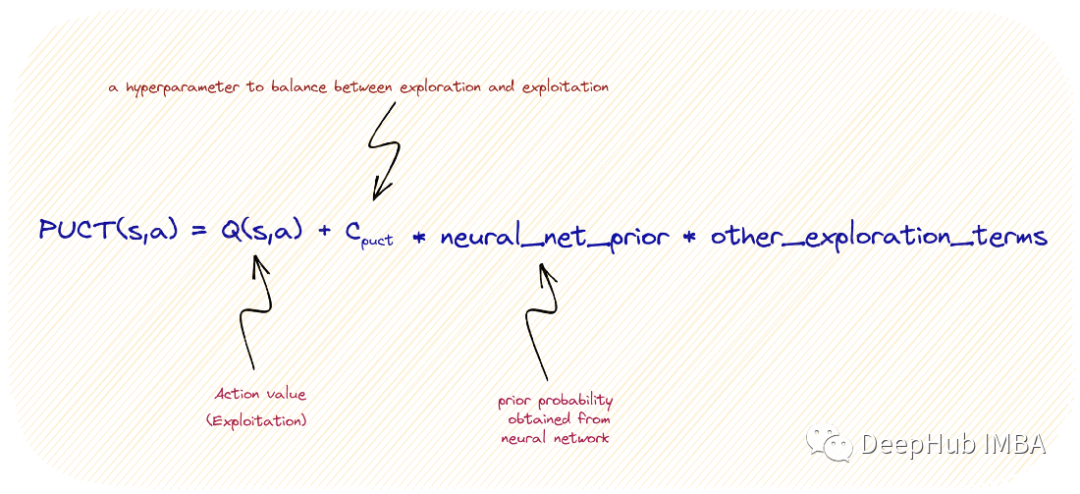
动作值Q(s, a)表示在状态s下通过动作a获得的平均奖励。一开始,Q(s, a)是零。这个action-value代表我们在任何给定时间对奖励函数的了解,因此它与使用有关。
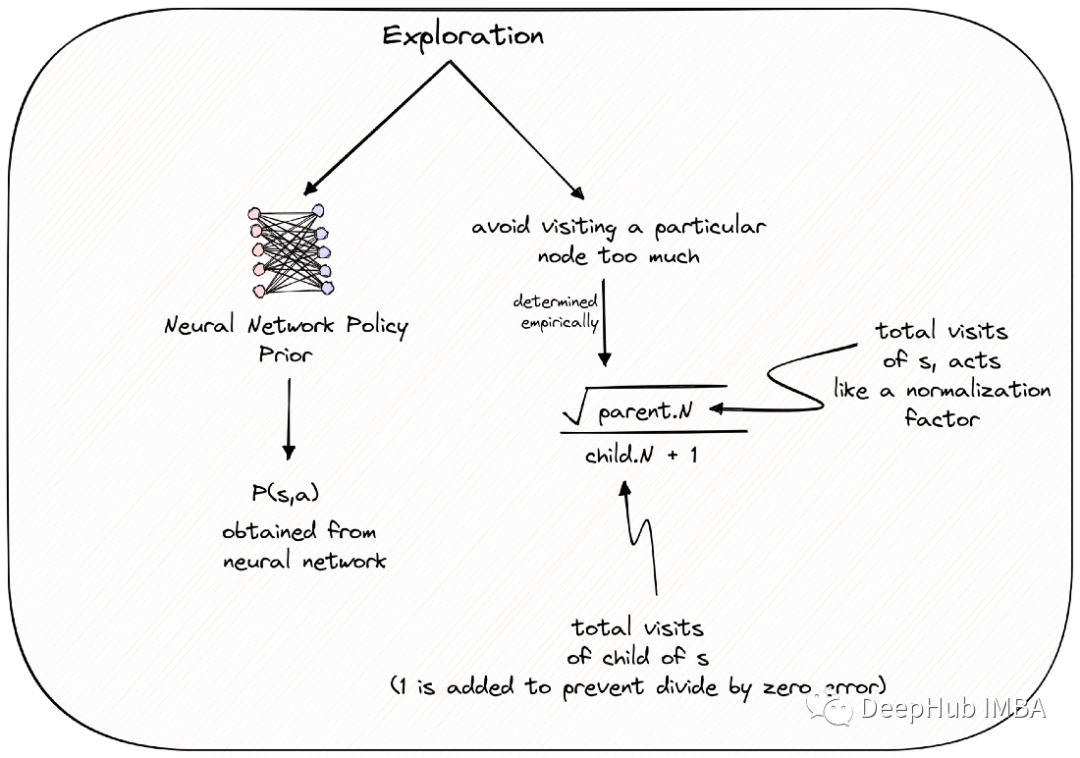
假设我们训练过的神经网络以0.3的概率表示我们应该执行某个动作a。那么将0.3的概率包含在PUCT规则的探索部分。状态s属于父节点,通过在“s”上执行动作“a”获得的状态属于子节点。但是这样会导致经常访问MCTS中的某个节点,为了避免这种情况并鼓励探索其他节点,子节点的访问计数包含在分母中,并使用父节点的总访问数进行规范化。
为什么要取父节点访问次数的平方根?PUCT规则是根据经验设计的,这是作者所尝试的所有选择中最有效的,也就是说是一个可以配置的超参数。我们也可以直接将其视为一种对子节点进行归一化的方式:分母中的 N+1 项。
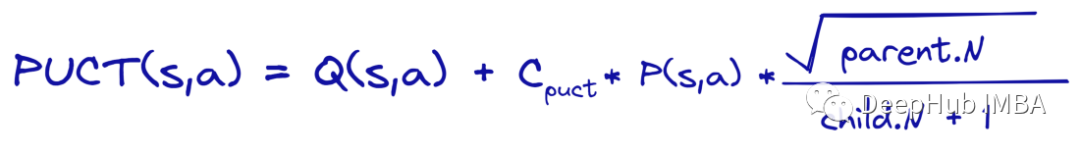
在上图中可以看到超参数c_puct。这个常数平衡探索采和使用条件。这个超参数的典型值是2。
现在已经对如何获得PUCT(s, a)有了一定的了解,让我们继续MCTS中的选择步骤。
选择步骤如下面的块所示,即从根节点开始,重复查找具有最大PUCT值的子节点,直到到达状态仍然为None(尚未展开/初始化)的节点。
consider_node = root// terminal nodes also have a None statewhile consider_node.state is not None:
best_node = find_child_with_maximum_puct_value(consider_node)
consider_node = best_nodeconsider_node has to be expanded
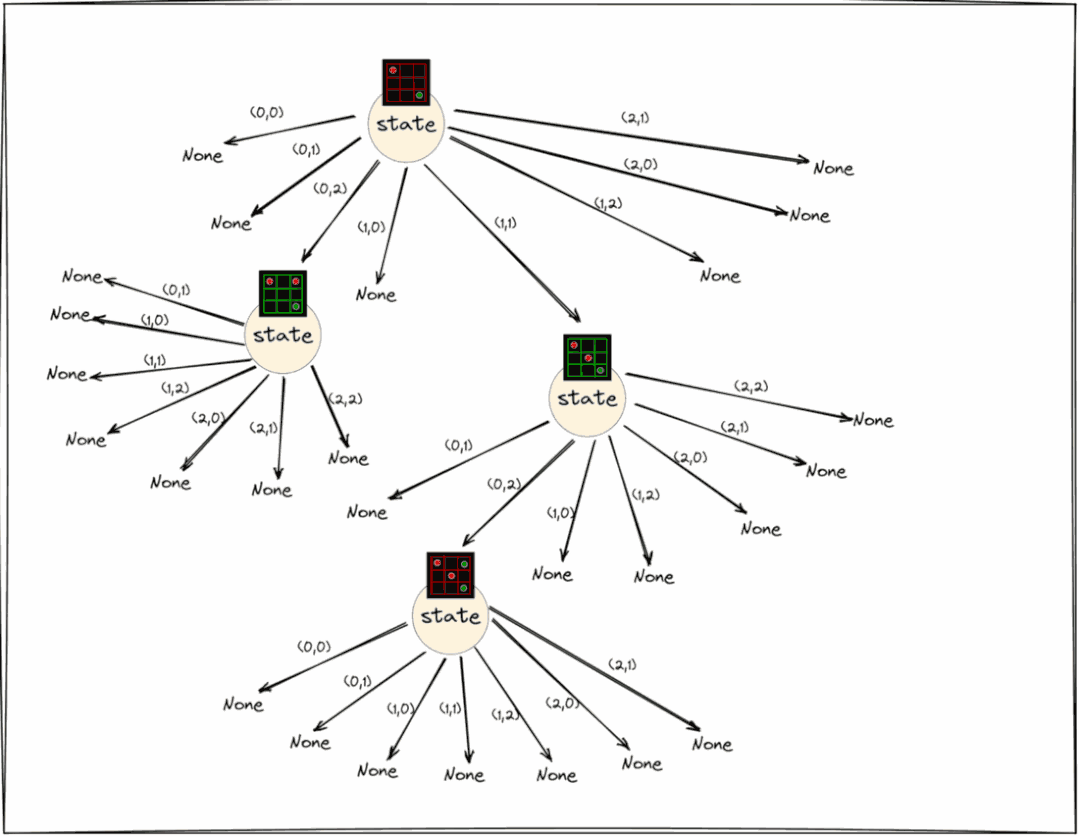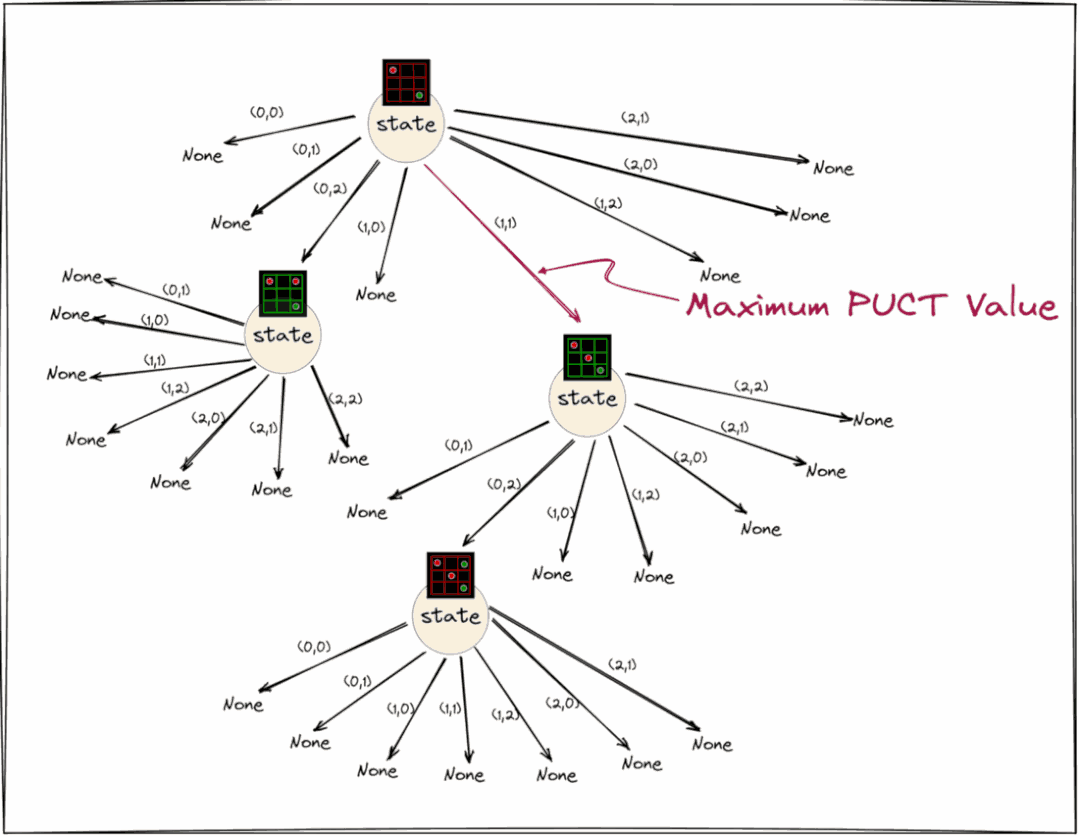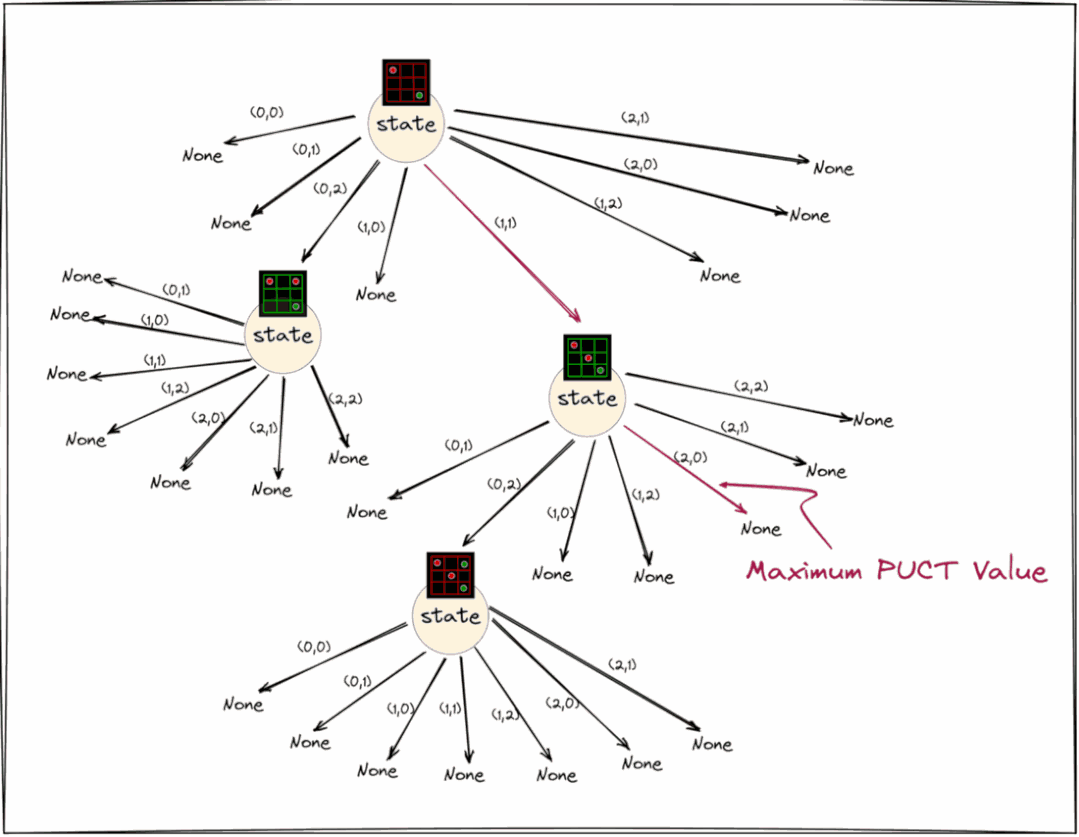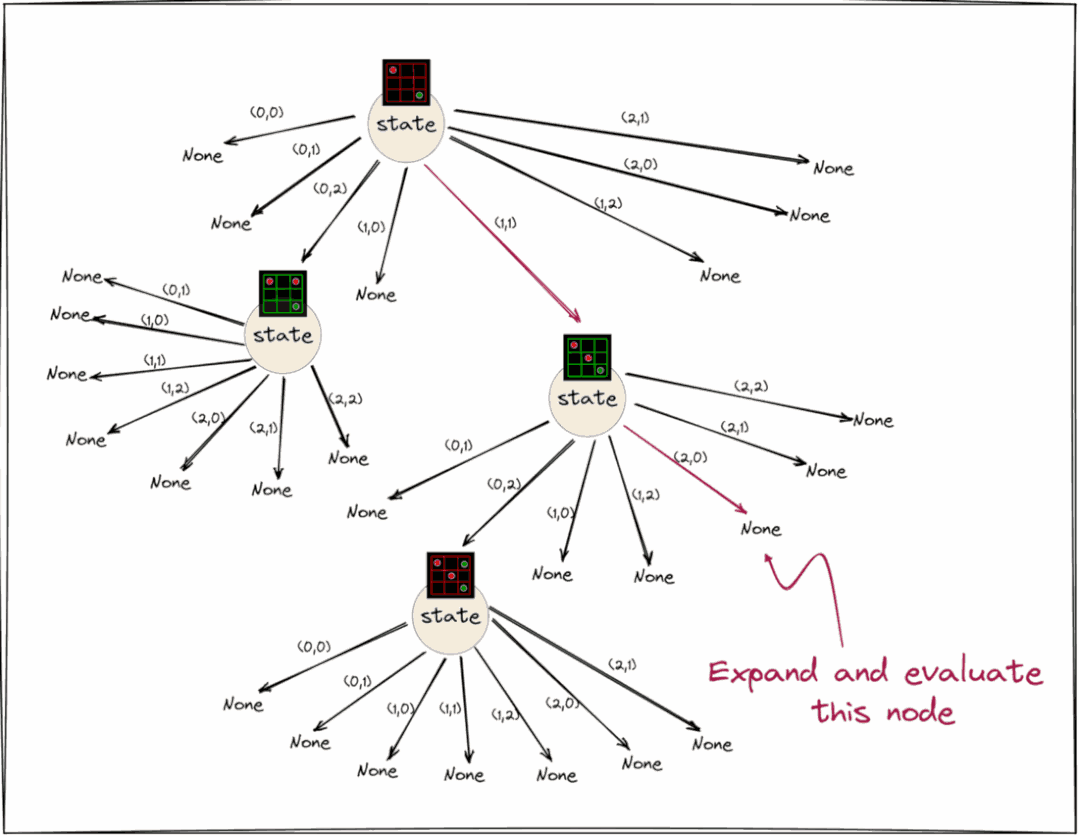
上面动图显示了重复查找pput值最大的子节点,直到到达状态仍然为None的节点
展开和求值
在选择了特定的动作后,下一步就就是展开并对该节点进行求值(因为其状态仍为 None)。这里的展开表示通过初始化选定节点的状态来扩展树。这种新的状态是从游戏规则中获得的。如果它是一个终端节点,我们将状态保留为 None 并在节点中设置一个标志,将其标记为带有获胜者信息的终端节点。
所选节点的所有新边也被初始化。例如上面动图中显示的树在展开所选节点后将如下图所示。
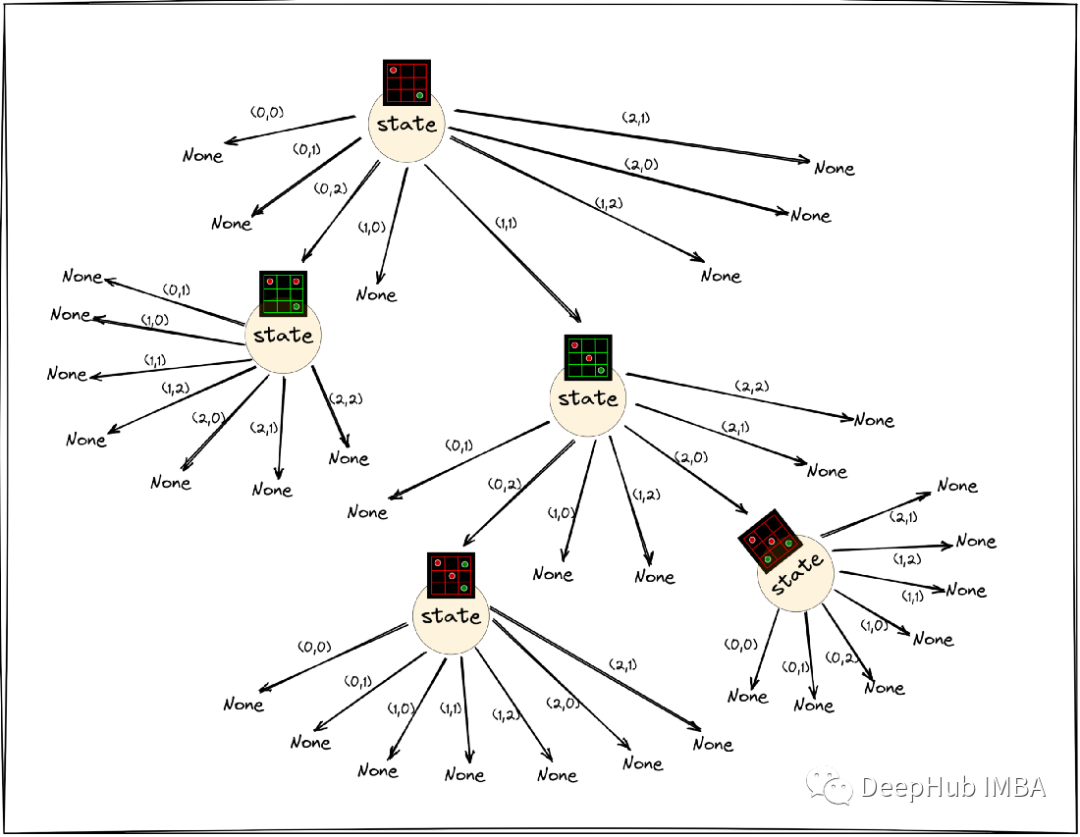
接下来就是展开节点的计算,评估指玩家在该节点的期望奖励。传统的 MCTS 使用 rollout 策略从扩展节点执行 rollout,以找出游戏结束时的值, 这个策略可以是均匀随机的。而AlphaZero的MCTS与传统的MCTS不同,在AlphaZero的MCTS中,使用神经网络的值输出来确定展开节点的值。
比如当评估一个国际象棋的位置时,我们会在脑海中计算一些走法,然后在计算结束时只使用的直觉来判断结果会有多好。在计算结束时不会像传统的 MCTS 那样进行操作,也不会在游戏结束之前使用随机动作模拟那个操作,我们只选择几个我们认为比较好的位置进行操作。
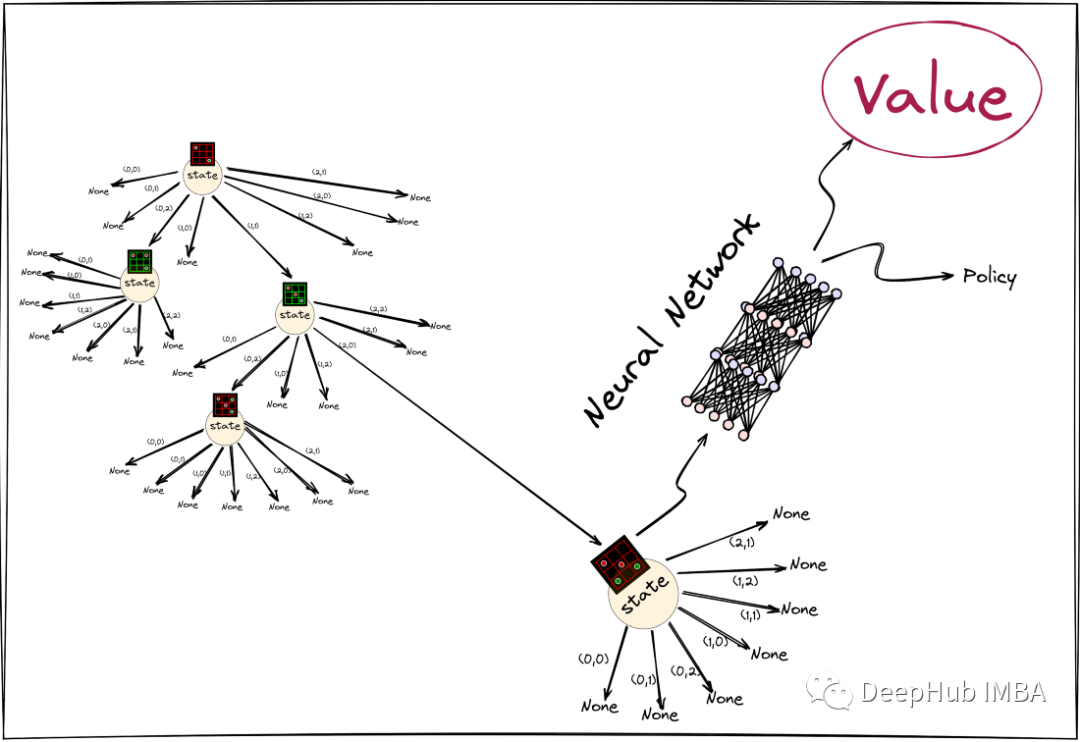
下面是代码的实现。
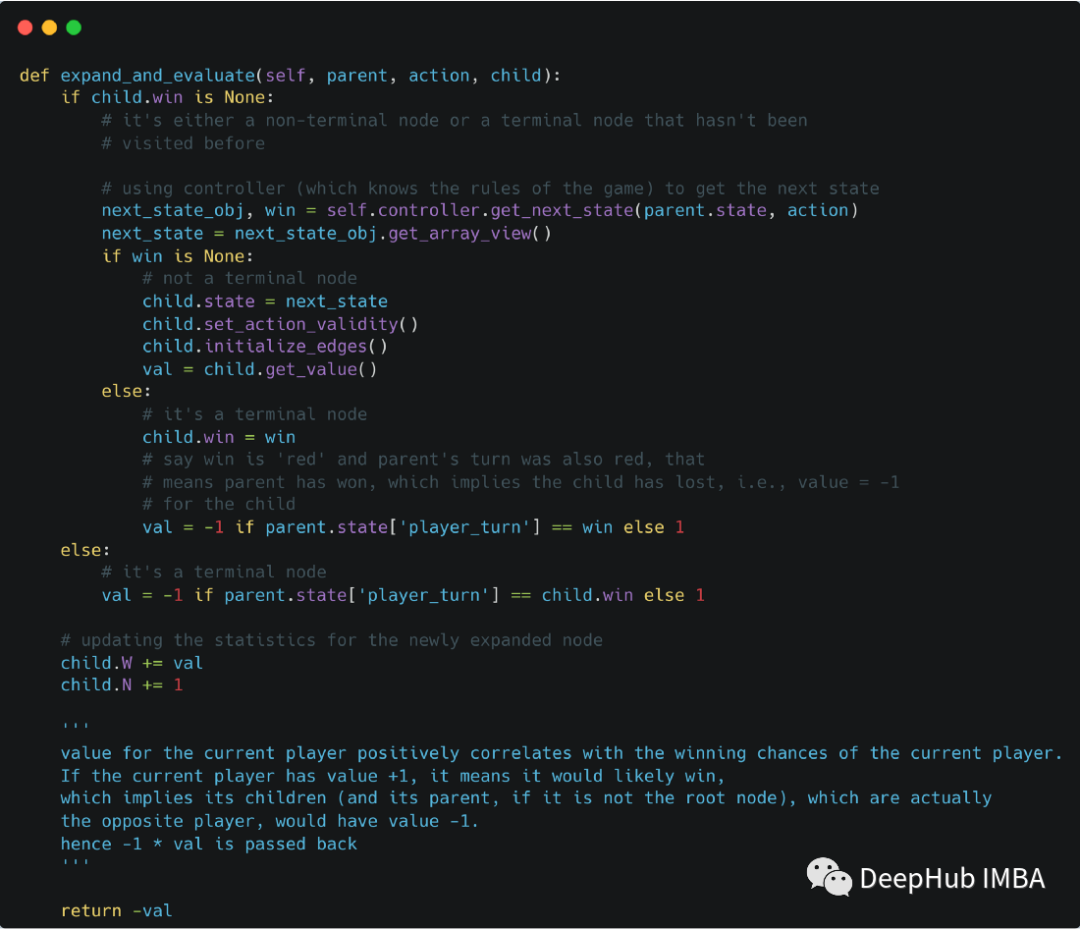
回溯
在对展开的节点进行评估之后,还需要更新从根节点到展开节点的所有节点的Q值(由总奖励值和总访问次数实现)。这被称为MCTS的回溯(Backup)步骤。
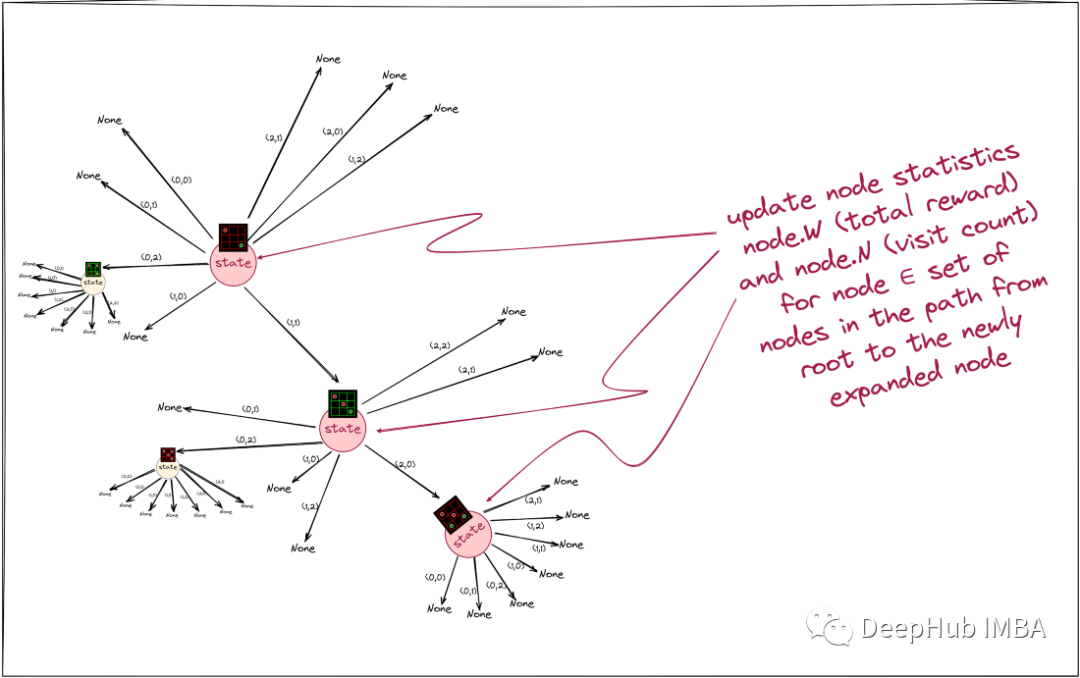
这一点的实现比较简单方法是使用递归地实现选择函数,
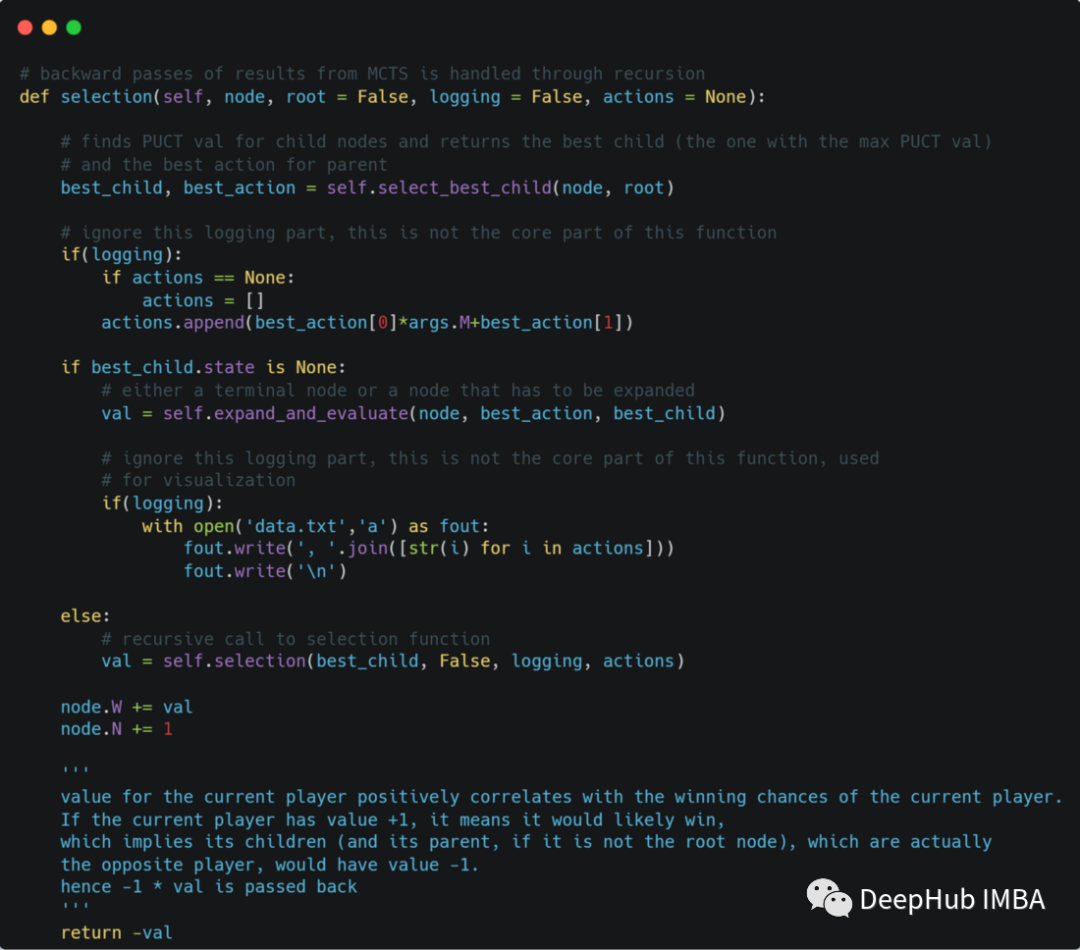
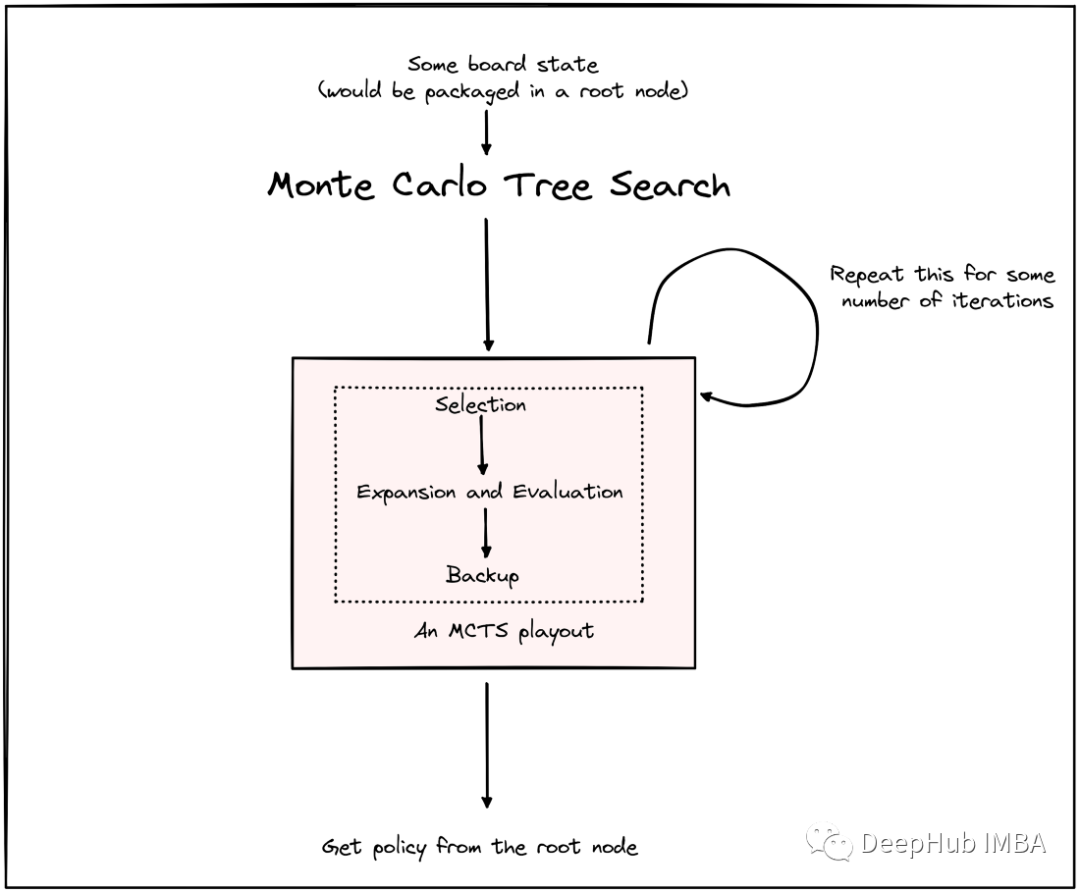
开始游戏
上面的四个步骤在一定次数的迭代中运行。如果它们运行了1000次迭代,那么总共将扩展最多1000个新节点(我们之所以说最大值,是因为某些终端节点可能被访问多次)。
在这些迭代结束后,观察根节点和它的子节点可能看起来像这样。
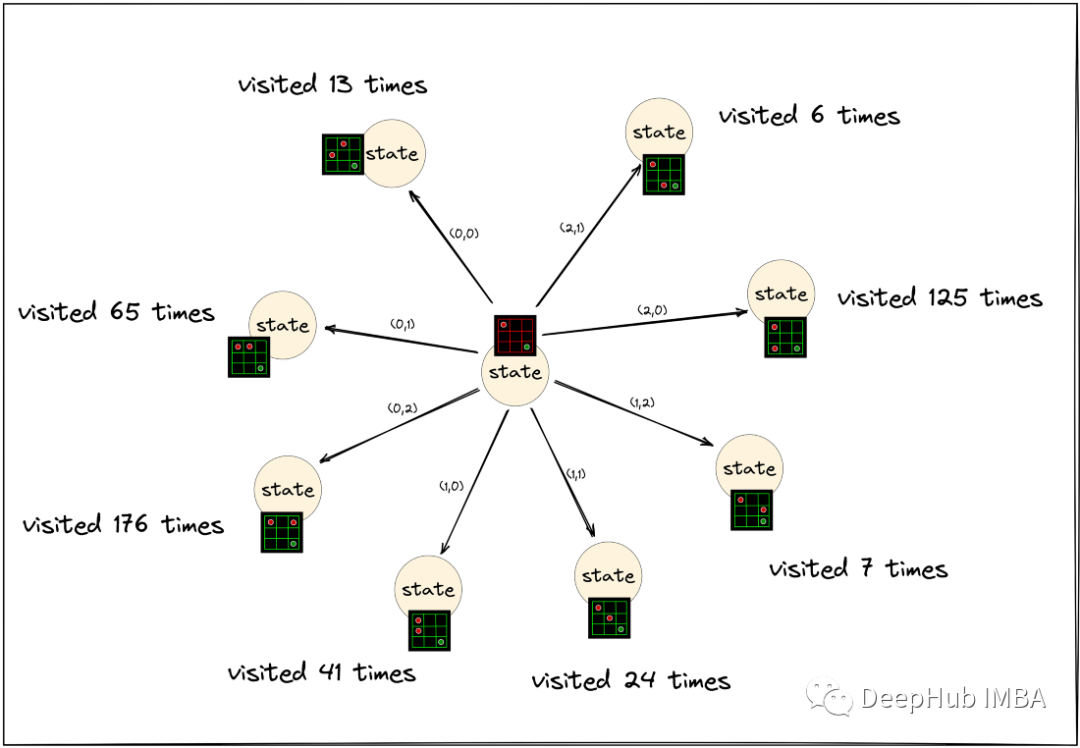
这些访问计数在根节点输出策略。AlphaZero 使用的想法是,如果一个节点被更多地访问,那么我们应该分配一个更高的概率来执行给该节点的根节点的动作。

某个动作的输出策略概率值与N^(1/τ)成正比,其中N是通过该动作获得的根节点子节点的访问次数,τ是某个温度(temperature )值。
从上图中我们可以看到,从AlphaZero中搜索获得的每个动作的输出策略与被提升为1/τ的结果子节点的访问计数成正比,其中τ是某个温度值。τ的高值将导致更统一的策略。可以在代码中设置为1。
然后从这个输出策略中抽样一些动作,为给定的状态进行一些操作。使用访问计数来构造输出策略是合理的,因为使用PUCT值来指导蒙特卡罗树搜索。这些PUCT价值观平衡了探索和使用。向根节点返回更多值的节点将被更频繁地访问,而一些节点将通过探索被随机访问。
这样整个AlphaZero的最基本的概念就介绍完了
References
[1] https://en.wikipedia.org/wiki/Monte_Carlo_method
[2] Silver, D., Hubert, T., Schrittwieser, J., Antonoglou, I., Lai, M., Guez, A., Lanctot, M., Sifre, L., Kumaran, D., Graepel, T., Lillicrap, T., Simonyan, K., & Hassabis, D. (2018). A general reinforcement learning algorithm that Masters Chess, Shogi, and go through self-play. Science, 362(6419), 1140–1144. https://doi.org/10.1126/science.aar6404
[3] Rosin, C. D. (2011). Multi-armed bandits with episode context. Annals of Mathematics and Artificial Intelligence, 61(3), 203–230. https://doi.org/10.1007/s10472-011-9258-6
[4] Danihelka, I., Guez, A., Schrittwieser, J., & Silver, D. Policy Improvement by planning with Gumbel. Deepmind. Retrieved February 23, 2022, from https://deepmind.com/research/publications/2022/Policy-improvement-by-planning-with-Gumbel
作者:Bentou