算法设计： 五、回溯法（1. 0-1 背包问题）—— C++实现 - 算法分析

回朔法

回朔法有通用解题法之称，可以系统地搜索一个问题的所有解或者任一解，
他是一个即带有系统性又带有跳跃性的搜索算法。

回朔法算法解题的一般思路：

1. 针对所给问题，定义问题的解空间；
2. 确定易于搜索的解空间结构；
3. 以深度优先的方式搜索解空间。

利用回朔法求解 0-1 背包问题。

我们有 n 种物品，物品 j 的重量为 wj，价格为 pj。我们假定所有物品的重
量和价格都是非负的。背包所能承受的最大重量为 c。如果限定每种物品只能选
择 0 个或 1 个。
有六件物品，体积和价值见下表，背包容量为 25
i(物品)123456w(体积)117912310v(价值)10579212

求解思想：

（1）定义问题解空间；
（2）确定易于搜索的解空间结构，该问题的解空间结构为子集树；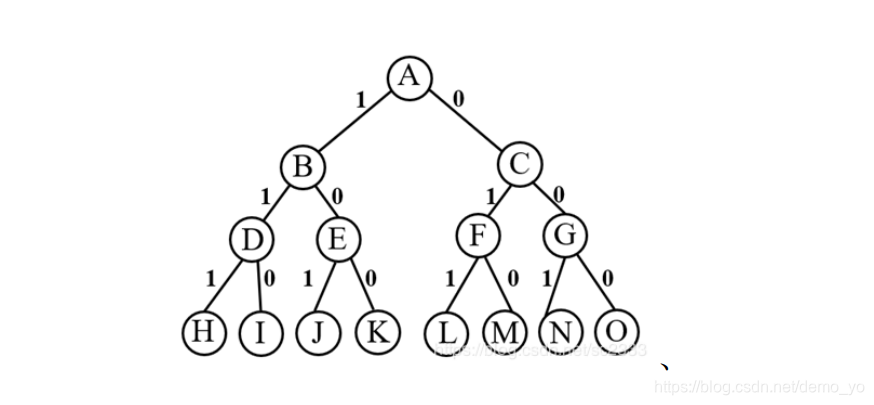

（3）采用深度优先方式搜索解空间，同时要及时剪枝，避免无效搜索。该问
题的限界函数为：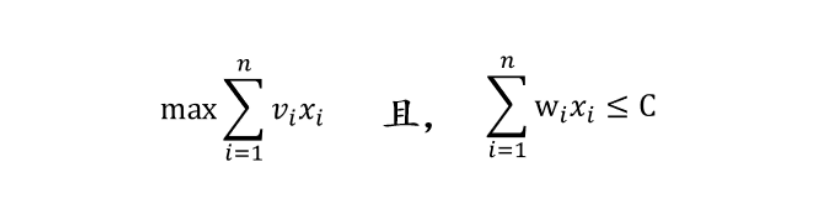

数据结构和变量：

typedefstruct{float        w;/* 物体重量 */float        p;/* 物体价值 */float        v;/* 物体的价值重量比 */} OBJECT;

OBJECT    ob[n];float        M;/* 背包载重量 */int        x[n];/* 可能的解向量 */int        y[n];/* 当前搜索的解向量 */float        p_est;/* 当前搜索方向装入背包物体的估计最大价值 */float        p_total;/* 装入背包的物体的最大价值的上界 */float        w_cur;/* 当前装入背包的物体的总重量 */float        p_cur;/* 当前装入背包的物体的总价值 */

0/1背包问题的回溯算法：

1.floatknapsack_back(OBJECT ob[],float M,int n,BOOL x[])2.{3.int i,k;4.float w_cur,p_total,p_cur,w_est,p_est;5.     BOOL *y =new BOOL[n];6.for(i=0;i<=n;i++){/* 计算物体的价值重量比 */7.         ob[i].v = ob[i].p / ob[i].w;8.         y[i]= FALSE;/* 当前的解向量初始化 */9.}10.merge_sort(ob,n);/* 物体按价值重量比的非增顺序排序*/11.     w_cur = p_cur = p_total =0;/* 当前背包中物体的价值重量初始化*/12.     k =0;/* 已搜索到的可能解的总价值初始化*/13.while(k>=0){14.         w_est = w_cur;   p_est = p_cur;15.for(i=k;i<n;i++){/* 沿当前分支可能取得的最大价值 */16.             w_est = w_est + ob[i].w;17.if(w_est<M){18.                 p_est = p_est + ob[i].p;19.else{20.                 p_est = p_est +((M – w_est + ob[i].w)/ ob[i].w)* ob[i].p;21.break;22.}23.}24.if(p_est>p_total){/* 估计值大于上界 */25.for(i=k;i<n;i++){26.if(w_cur+ob[i].w<=M){/* 可装入第i个物体 */27.                     w_cur = w_cur + ob[i].w;28.                     p_cur = p_cur + ob[i].p;29.                     y[i]= TRUE;30.}31.else{32.                     y[i]= FALSE;break;/* 不能装入第i个物体 */33.}34.}35.if(i>=n){/* n个物体已全部装入 */36.if(p_cur>p_total){37.                     p_total = p_cur;   k = n;/* 刷新当前上限 */38.for(i=0;i<n;i++)/* 保存可能的解 */39.                         x[i]= y[i];40.}41.}42.else k = i +1;/* 继续装入其余物体 */43.}44.else{/* 估计价值小于当前上限*/45.while((i>=0)&&(y[i]==0)/* 沿着右分支结点方向回溯*/46.                 i = i – 1;/* 直到左分支结点 */47.if(i<0)break;/* 已到达根结点,算法结束 */48.else{49.                 w_cur = w_cur – ob[i].w;/* 修改当前值 */50.                 p_cur = p_cur – ob[i].p;51.                 y[i]= FALSE;   k = i +1;/* 搜索右分支子树 */52.}53.}54.}55.delete y;56.return p_total;57.}

算法分析

算法在最坏情况下所花费的时间： O(n·2n)
合并排序，需花费 O(n·log n) 时间；
在最坏情况下，状态空间树有 2n+1-1个结点，有 O(2n) 儿子结点，
每个右儿子结点都需估计继续搜索可能取得的目标函数的最大价值，每次估计时间需花费 O(n) 时间，因此，右儿子结点需花费 O(n·2n) 时间

工作空间为：O(n)