《LeetCode》—— 买卖股票的最佳时机

本期，我将给大家讲解的是有关动态规划类的题——买卖股票的最佳时机。这个系列总共有四道题。接下来，让我们一起去看看！！！

（一）买卖股票的最佳时机

LeetCode题目链接：买卖股票的最佳时机

题目如下：

题目分析：

第一题，我们先来看最简单的（题目的难度也是逐级提升的）。

• 思路一：

首先，我们有的小伙伴一读题，最先想到的可能就是暴力去求解这道题目，但是很遗憾当我们提交代码的时候显示的是代码超时了。因此，很显然暴力解法显然不是出题者要考察我们的地方。

• 思路二：

那么暴力求解不行，还有没有其他思路呢？我们通过分析题目，主要意思就是找到最多一次买卖股票可以获得的最大利润的问题的解决方案。我们可以利用贪心的思路来分析，主要原理是跟踪到目前为止看到的最低价格和以当前价格卖出可以获得的最大利润，通过迭代价格并相应地更新这些值，我们可以找到可以获得的最大利润。

• 思路三：

那么除了上述的贪心去求解还有没有其他思路呢？其实还有一种我们今天主要讲的动态规划算法。

解题思路：

在这里，我只给出动态规划的具体实现过程。

• step1：确定【arry】数组以及下标的含义

**首先，我们初始化一个二维数组 arry，其中大小是价格向量的大小（size为给出的数组

prices 的大小

），arry 中每行的第一个元素表示买入或者卖出的天数，第二个元素表示当天的状态。**

arry[i][0]：

• 表示第i天持有股票所得最多现金 。因为刚开始时没钱买，所以开始现金是0，因此第i天买入股票现金就是 -prices[i]， 这是一个负数；
• arry[0][0]表示第0天持有股票，此时的持有股票就一定是买入股票了，因为不可能有前一天推出来，所以arry[0][0] -= prices[0];

arry[i][1]：

• 表示第i天不持有股票所得最多现金，即也许是一直都还没有没有买入，或者要卖出；
• arry[0][1]表示第0天不持有股票，不持有股票那么现金就是0，所以arry[0][1] = 0;

• step2：确定递推公式

如果第i天持有股票即arry[i][0]， 那么递归公式可以像如下这样：

• 如果在当前前的前一天即（ i-1） 天就持有股票的话，那么当前所持有的现金就是昨天持有股票的所得现金 即：arry[i - 1][0]
• 如果是在当前这一天买入股票即（i），那么此时所持有的就是买入今天的股票后所得现金即：-prices[i]（为负数）

💨 arry[i][0] = max(arry[i - 1][0], -prices[i])

如果第i天不持有股票即arry[i][1]， 那么递归公式可以像如下这样：

• 如果在第（i-1）天未持有股票，那么就保持现状，所得现金就是昨天不持有股票的所得现金 即：arry[i - 1][1]
• 如果在第（ i ）天卖出股票，所得现金就是按照今天股票价格卖出后所得现金即：prices[i] + arry[i - 1][0]

💨 arry[i][1] = max(arry[i - 1][1], prices[i] + arry[i - 1][0])

• step3：确定遍历顺序

从递推公式可以看出arry[i]都是由arry[i - 1]推导出来的，因此是从前向后遍历

• step4：图解展示

代码展示：

• 暴力解法：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
    int n = (int)prices.size()；
    int res = 0;
        for (int i = 0; i < n; ++i){
            for (int j = i + 1; j < n; ++j) {
                res = max(res, prices[j] - prices[i]);
            }
        }
        return res;
   }
};

性能分析：

• 时间复杂度：O(n^2)

• 空间复杂度：O(1)

• 贪心算法：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int num = INT_MAX;
        int res = 0;
        for (int i = 0; i < prices.size(); i++) {
            num = min(num, prices[i]); 
            res = max(res, prices[i] - num); 
        }
        return res;
    }
};

性能分析：

• 时间复杂度：O(n)

• 空间复杂度：O(1)

• 动态规划：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int size = prices.size();
        if (size == 0) 
            return 0;
        vector<vector<int>> arry(size, vector<int>(2));
        arry[0][0] -= prices[0];
        arry[0][1] = 0;
        for (int i = 1; i < size; i++) {
            arry[i][0] = max(arry[i - 1][0], -prices[i]);
            arry[i][1] = max(arry[i - 1][1], prices[i] + arry[i - 1][0]);
        }
        return arry[size - 1][1];

    }
};

性能分析：

• 时间复杂度：O(n)
• 空间复杂度：O(n)

（二）买卖股票的最佳时机 II

LeetCode题目链接：买卖股票的最佳时机 II

题目如下：

题目分析：

大家通过分析这道题，我们可以发现这道题跟上道题目的差别就在于本题股票可以进行多次的买卖操作（注意只有一只股票，所以再次购买前要出售掉之前的股票）。

• 思路一：

**小伙伴们看到这道题目想的就是 -- **选一个低的买入，再选个高的卖，再选一个低的买入.....循环反复。

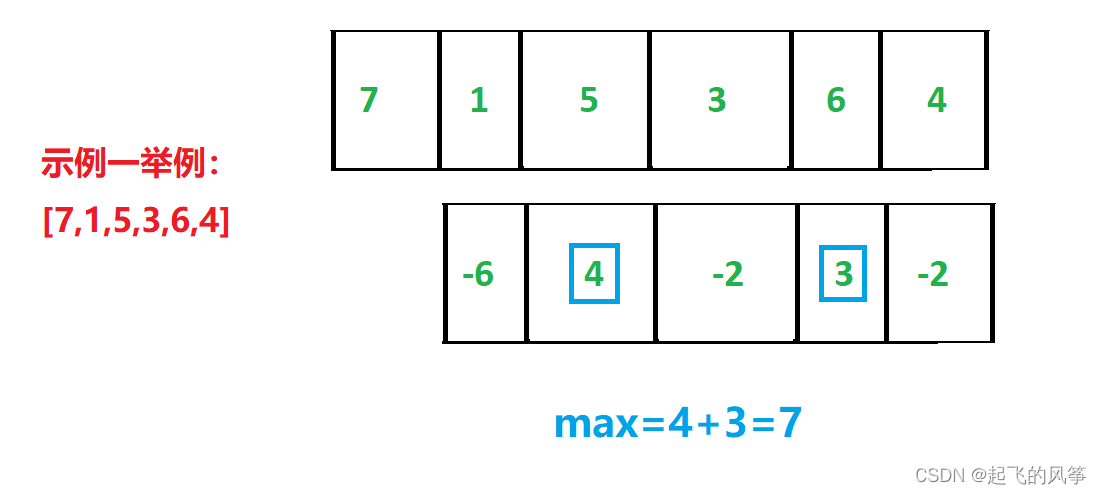
其实，我们对这种思路进行分解 -- 只收集正利润，即最终的最大利润就是各天的正利润之和。

对于每次迭代，我们可以计算出价格向量中当前元素与前一个元素之间的差值，并取该差值和0中较大的值，这样做确保仅将正差异添加到 res 变量中，仅使用单个循环来迭代价格向量并计算最大利润

• 思路二：

还是利用动态规划的思想对其进行操作。

解题思路：

因为本题跟上一题是类似的，不同的在关于递推公式，接下来，我就只讲递推公式的演化，其余的跟上题相同。

如果第i天持有股票即arry[i][0]， 那么递归公式可以像如下这样：

这题因为是可以进行多次的买卖的，因此递归公式主要的变化就发生在对于 arry[i][0] 的处理，所以当第（i）天买入股票的时候，所持有的现金可能是在这之前已经经过买卖交易所得到的。

因此，对于第（i）天持有股票即 arry[i][0]：如果是第（i）天买入股票，所得现金就是昨天不持有股票的所得现金 减去 当天的股票价格 即：arry[i - 1][1] - prices[i]。

💨 arry[i][0] = max(arry[i - 1][0], arry[i - 1][1] - prices[i])

如果第i天持有股票即arry[i][1]， 递归公式跟上题相同

💨 arry[i][1] = max(arry[i - 1][1], prices[i] + arry[i - 1][0])

代码展示：

• 贪心算法：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
         int res=0;
         for(int i=1; i<prices.size(); ++i)
         {
             res+=max(prices[i]-prices[i-1],0);
         }
         return res;
    }
};

性能分析：

• 时间复杂度：O(n)

• 空间复杂度：O(1)

• 动态规划：

class Solution {
    public:
        int maxProfit(vector<int>& prices) {
        int size = prices.size();
        vector<vector<int>> arry(size, vector<int>(2, 0));
        arry[0][0] -= prices[0];
        arry[0][1] = 0;
        for (int i = 1; i < size; i++) {
            arry[i][0] = max(arry[i - 1][0], arry[i - 1][1] - prices[i]); 
            arry[i][1] = max(arry[i - 1][1], arry[i - 1][0] + prices[i]);
        }
        return arry[size - 1][1];
    }
};

性能分析：

• 时间复杂度：O(n)
• 空间复杂度：O(n)

（三）买卖股票的最佳时机 III

LeetCode题目链接：买卖股票的最佳时机 III

题目如下：

题目分析：

这道题跟上述两道题的不同之处在于对买卖的次数限制为 至多买卖两次，这意味着可以买卖一次，可以买卖两次，也可以不买卖。

解题思路：

• step1：确定【arry】数组以及下标的含义

在这道题目，我们就需要设置 5个状态位来表示了，因为题目已经明确给出了之多买卖两次，因此在加上操作的情况，总共就有5种。

• 0、表示没有任何操作
• 1、第一次买入股票
• 2、第一次卖出股票
• 3、第二次买入股票
• 4、第二次卖出股票

💨 arry[i][j] 中 i 表示第i天，j为 [0 - 4] 五个状态，arry[i][j] 表示第i天状态j所剩最大现金。

arry[0][0]：

开始时没有任何操作，因此应该为0，即：arry[0][0] = 0;

arry[0][1]：

在第0天准备进行第一次购买操作，所以此时应为：arry[0][1] = -prices[0];

arry[0][2]：

大家可以理解当天买入，当天卖出，所以 arry[0][2] = 0;

arry[0][3]：

第0天第二次买入操作，初始值应该是多少呢？应该不少同学疑惑，第一次还没买入呢，怎么初始化第二次买入呢？

第二次买入依赖于第一次卖出的状态，其实相当于第0天第一次买入了，第一次卖出了，然后再买入一次（第二次买入），那么现在手头上没有现金，只要买入，现金就做相应的减少。

所以第二次买入操作，初始化为：arry[0][3] = -prices[0];

arry[0][4]：

第二次卖出股票，应为arry[0][4] = 0;

• step2：确定递推公式

如果第i天第一次买进股票即arry[i][1]， 那么递归公式可以像如下这样：

• 如果第i天第一次买入股票了，那么** arry[i][1] = arry[i-1][0] - prices[i]**
• 如果第i天没有进行任何操作，则保持前一天买入的状态，即：arry[i][1] = arry[i - 1][1]

💨 arry[i][1] = max(arry[i-1][0] - prices[i], arry[i - 1][1])

如果第i天第一次卖出股票即arry[i][2]， 那么递归公式可以像如下这样：

• 如果第i天第一次卖出股票了，那么** arry[i][2] = arry[i - 1][1] + prices[i]**
• 如果第i天没有操作，则保持前一天卖出股票的状态，即：arry[i][2] = arry[i - 1][2]

💨 arry[i][2] = max(arry[i - 1][1] + prices[i], arry[i - 1][2])

如果第i天第二次买进股票即arry[i][3]， 那么递归公式可以像如下这样：

• 如果第i天第二次买入股票了，那么** arry[i][3] = arry[i-1][2] - prices[i]**
• 如果第i天没有进行任何操作，则保持前一天买入的状态，即：arry[i][3] = arry[i - 1][3]

**💨 arry[i][3] = max(arry[i - 1][2] - prices[i], arry[i - 1][3])
**

如果第i天第二次卖出股票即arry[i][4]， 那么递归公式可以像如下这样：

• 如果第i天第二次卖出股票了，那么** arry[i][4] = arry[i - 1][3] + prices[i]**
• 如果第i天没有操作，则保持前一次卖出股票的状态，即：arry[i][4] = arry[i - 1][4]

💨arry[i][4] = max(arry[i - 1][3] + prices[i], arry[i - 1][4])

• step3：遍历顺序

从递归公式可以看出，一定是从前向后遍历，因为arry[i]，依靠arry[i - 1]的数值。

• step4：图解展示

代码展示：

以下给出的是优化后的版本（大家可以根据理解写出原始版本）

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if(prices.size() == 0) return 0;

        vector<int> arry(5,0);
        arry[1] = -prices[0];
        arry[3] = -prices[0];

        for(int i=1; i<prices.size(); ++i){
            arry[1] = max(arry[1], arry[0] - prices[i]);
            arry[2] = max(arry[2], arry[1] + prices[i]);
            arry[3] = max(arry[3], arry[2] - prices[i]);
            arry[4] = max(arry[4], arry[3] + prices[i]);     
            
        }
        return arry[4];
      
    }
};

性能分析：

• 时间复杂度：O(n)
• 空间复杂度：O(1)

（四）买卖股票的最佳时机 IV

LeetCode题目链接：买卖股票的最佳时机 IV

题目如下：

题目分析：

这道题总体说来就是上一题的进阶版本，对于买卖的次数又进行了限制，这里要求至多有k次交易。

解题思路：

整体思路还是跟上题一样，只是本题对于次数是k次

• step1：确定【arry】数组以及下标的含义

此时状态就不仅仅有4种了（除去没有任何操作），而是2k种，如果加上不做任何操作的状态，那此处的状态就有 2k+1 次。

• step2：确定递推公式

同上（大家自己推倒看看能否推倒出来）

• step3：遍历顺序

同上

• step4：图解展示

大家可以对比上一题的图自己画图试试

代码展示：

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        if (prices.size() == 0) return 0;
        vector<vector<int>> arry(prices.size(), vector<int>(2 * k + 1, 0));
        for (int j = 1; j < 2 * k; j += 2) {
            arry[0][j] = -prices[0];
        }
        for (int i = 1;i < prices.size(); i++) {
            for (int j = 0; j < 2 * k - 1; j += 2) {
                arry[i][j + 1] = max(arry[i - 1][j + 1], arry[i - 1][j] - prices[i]);
                arry[i][j + 2] = max(arry[i - 1][j + 2], arry[i - 1][j + 1] + prices[i]);
            }
        }
        return arry[prices.size() - 1][2 * k];
    }
};

到此，关于购买股票的几个题便讲解完毕了。希望对大家有所帮助，感谢各位的观看！！！