细谈RSA加密算法

细谈RSA加密算法

   RSA加密算法是计算机科学中最广泛使用的公钥加密算法之一。RSA加密算法是基于数学上的不可解性问题，使用了一对密钥：公钥和私钥。公钥可以给任何人公开，私钥只能由特定的用户持有。本文将深入探讨RSA加密算法，讲解其加密、解密过程、加解密例子及实际应用。

一、RSA加密算法的历史和发展

   RSA加密算法是由罗纳德·李维斯特（Ronald Linn Rivest）、阿迪·萨莫尔（Adi Shamir）和伦纳德·阿德尔曼（Leonard Adleman）于1977年共同发明的。RSA三人分别是美国麻省理工学院（MIT）的教授。

   随着计算机技术的发展，RSA加密算法得到了广泛的应用。它不仅被用于电子邮件、网上银行等互联网应用中，还被用于服务器间的数据传输加密。

二、RSA加密算法的原理

   RSA加密算法是利用大素数因数分解的困难性来保证信息传输的安全。现代计算机的算力很强，可以轻松地找出两个很大质数的乘积，但是如果这个乘积非常大，那么就非常难以将其分解为质因数。

   例如，200位的十进制数，其因数分解需要3亿年的时间，这个时间是超出人类耐心的极限。因此，只要我们使用一个足够长的素数，就可以保证其不被分解。

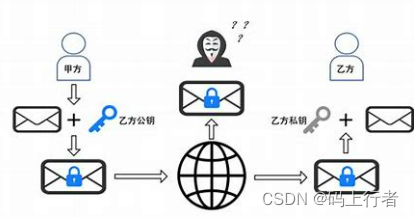
   RSA加密算法涉及到两个关键因素：公钥和私钥。公钥是可以公开的，而私钥只有其持有者才能访问。

1.密钥生成

RSA加密算法密钥生成的过程如下：

（1）选择两个大素数p、q，且p不等于q；

（2）计算n=pq；

（3）计算φ(n)=(p-1)(q-1)；

（4）选择一个整数e，1<e<φ(n)，且e与φ(n)互质；

（5）计算d，满足ed ≡ 1 (mod φ(n))，换言之，d是关于φ(n)的乘法逆元。即ed % φ(n) = 1，其中%表示求余运算。

公钥为(n,e)，私钥为(n,d)。

2.加密过程

RSA加密过程如下：

（1）明文数据转化为数字m（可以是字符串、图片或其他数据）；

（2）将m进行加密，得到c ≡ m^e (mod n)。

3.解密过程

RSA解密过程如下：

（1）公钥接收的密文是c；

（2）利用私钥d进行解密，得到m ≡ c^d (mod n)。

三、一个例子

“码上行者”的RSA加密过程如下：

1. 明文数据转化为数字m

将明文“码上行者”转化为ASCII码，得到的数字串为：

233 168 187 228 186 150 229 191 151

2. 生成密钥对

选择两个较大的素数p=9973和q=9967。

计算n=p*q=99407391

计算φ(n)=(p-1)(q-1)=99406432

选择一个整数e，1<e<φ(n)，且e与φ(n)互质。令e=1351。

计算d，满足ed ≡ 1 (mod φ(n))，即d=59484359。因此，公钥为(n=99407391,e=1351)，私钥为(n=99407391,d=59484359)。

3. 将数字m进行加密

对于文本信息“码上行者”，将其对应的数字串作为明文数字m，用公钥(n,e)来进行加密，即计算c ≡ m^e (mod n)。按照RSA加密算法的原理，有：

• c1 ≡ 233^1351 (mod 99407391)
• c2 ≡ 168^1351 (mod 99407391)
• c3 ≡ 187^1351 (mod 99407391)
• c4 ≡ 228^1351 (mod 99407391)
• c5 ≡ 186^1351 (mod 99407391)
• c6 ≡ 150^1351 (mod 99407391)
• c7 ≡ 229^1351 (mod 99407391)
• c8 ≡ 191^1351 (mod 99407391)
• c9 ≡ 151^1351 (mod 99407391)

将每个ci转换为十六进制，得到密文串为：

• 6aeb3c0f3a3e81d3827fcd9073560115f4d7169b464b5d0950236d0826cdbb5d
• 6706c0d85f51fc633c79476ffc461a9d40b787619eff1edbd4f592205da3ba67
• 881fa38d4e9ea79907c4c4f6e867e856dd20a4b05d14fb08486946f8453d51a5
• 339ea871e6db2ac1fc0a573b93eccb0ab5a0f44533b75ad6ae73f865143107e9
• 65c69d0e2b6a59fd3191fb378bc8fb2faf4365c4958b262836e295dcccd9c7f6
• 5fe6d493ffdfb21fb965e17bcf9250bc84b82a81cb8ebd4d57ea298b94fef4cd
• 99da7208d04e7c74ea7da8a7d69c33c3e8896d5c93904a2be9e1d1002f6b1a3f
• d25fcbfaa4b499faad37b3c1cfbb461ba4e90f3c4b68559403df9a4d40abc5f1
• 722a47572b4d3c1560e22c95f82ebc2011fcf026b3bd372f30a9f0d3725d92c6

4. 将密文c发送给接收方

将密文串发送给接收方，接收方使用私钥(n,d)进行解密，即计算 m ≡ c^d (mod n)。

按照RSA解密算法的原理，有：

• 233 ≡ c1^59484359 (mod 99407391)

• 168 ≡ c2^59484359 (mod 99407391)

• 187 ≡ c3^59484359 (mod 99407391)

• 228 ≡ c4^59484359 (mod 99407391)

• 186 ≡ c5^59484359 (mod 99407391)

• 150 ≡ c6^59484359 (mod 99407391)

• 229 ≡ c7^59484359 (mod 99407391)

• 191 ≡ c8^59484359 (mod 99407391)

• 151 ≡ c9^59484359 (mod 99407391)

   将解密后得到的数字转换成对应的ASCII码，得到原始明文信息为：“码上行者”。
  
   综上所述，针对明文“码上行者”，我们使用RSA加密过程进行了加密，得到了密文，再使用RSA解密过程进行解密，成功还原出原始明文。RSA加密算法使用随机生成的密钥对进行加密和解密，可以保护通信过程中的信息安全和机密性。
  

四、RSA加密算法的实际应用

   RSA加密算法广泛应用于对敏感信息的加密，例如信用卡号、社保卡号等保密信息的传输。

   RSA加密算法被广泛应用的另外一个领域是数字签名。数字签名是一种数字加密技术，用于验证电子文档的完整性和真实性。

   数字签名可以用于证明文档的作者身份和文档的原始性。数字签名也能够保证文档完整性，即任何修改文档的行为都会使数字签名失效。

   在互联网领域，RSA加密算法也被用于保护通过网络传输的数据。例如在SSL/TLS安全通信协议中，服务器和客户端之间的通信会使用RSA算法来进行加密和解密，从而确保数据的安全传输。此外，RSA加密算法也被用于数字支付、VPN等领域。

   在实际应用中，和许多加密算法一样，RSA算法也存在一些安全上的问题。其中最主要的问题是密钥生成和管理。密钥生成时需要选择足够的大质数，以确保公钥和私钥的强度。而在密钥的管理过程中，也必须严格保护密钥的机密性和完整性，防止密钥被泄露或篡改。

   另外，由于RSA加密算法运算量较大，因此在实际应用中，通常会采用混合加密的方式。例如，对称加密算法在传输过程中采用RSA算法加密的会话密钥，以保证加密安全性，同时保证了效率。这样，既保证了安全性，又能够保持高效。

五、结论

   总体来说，RSA加密算法是一种非常重要的加密算法，被广泛应用于网络安全中。通过其密钥生成、加密和解密的过程，可以实现数据加密和保密传输。虽然RSA加密算法存在一些安全上的问题，但是在实际应用中，通过采用合适的密钥生成和管理，以及混合加密的方式，可以保证加密安全性的同时，也能保持高效。

   未来，对于RSA算法的应用，以及对其安全性的研究，将会成为一个重要的研究方向。随着计算机技术的不断发展，RSA算法中的某些弊端可能被攻克，或者将由其他更安全的加密算法所取代，这都需要不断投入人力和资源进行研究和发展。