TensorFlow Probability是一个构建在TensorFlow之上的Python库。它将我们的概率模型与现代硬件(例如GPU)上的深度学习结合起来。
极大似然估计
最大似然估计是深度学习模型中常用的训练过程。目标是在给定一些数据的情况下,估计概率分布的参数。简单来说,我们想要最大化我们在某个假设的统计模型下观察到的数据的概率,即概率分布。
这里我们还引入了一些符号。连续随机变量的概率密度函数大致表示样本取某一特定值的概率。我们将表示这个函数𝑃(𝑥|𝜃),其中𝑥是样本的值,𝜃是描述概率分布的参数:
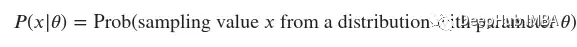
tfd.Normal(0, 1).prob(0)
<tf.Tensor: shape=(), dtype=float32, numpy=0.3989423>
当从同一个分布中独立抽取多个样本时(我们通常假设),样本值𝑥1,…,𝑥𝑛的概率密度函数是每个个体𝑥𝑖的概率密度函数的乘积:
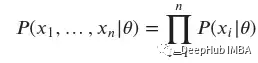
可以很容易地用一个例子来计算上面的问题。假设我们有一个标准的高斯分布和一些样本:𝑥1=−0.5,𝑥2=0和𝑥3=1.5。正如我们上面定义的那样,我只需要计算每个样本的概率密度函数,并将输出相乘。
X = [-0.5, 0, 1.5]
np.prod(tfd.Normal(0, 1).prob(X))
0.01819123
现在,我想直观地告诉大家概率密度函数和似然函数之间的区别。它们本质上是在计算类似的东西,但角度相反。
从概率密度函数开始,我们知道它们是样本𝑥1,…,𝑥𝑛的函数。参数𝜃被认为是固定的。因此当参数𝜃已知时,我们使用概率密度函数,找出相同样本𝑥1,…,𝑥𝑛的概率。简单地说,当我们知道产生某个过程的分布并且我们想从它中推断可能的抽样值时,我们使用这个函数。
对于似然函数,我们所知道的是样本,即观测数据𝑥1,…,𝑥𝑛。这意味着我们的自变量现在是𝜃,因为我们不知道是哪个分布产生了我们观察到的这个过程。所以当我们知道某个过程的样本时,使用这个函数,即我们收集了数据,但我们不知道最初是什么分布生成了该过程。也就是说既然我们知道这些数据,我们就可以对它们来自的分布进行推断。
对于似然函数,惯例是使用字母𝐿,而对于概率密度函数,我们引入了上面的符号。我们可以这样写:
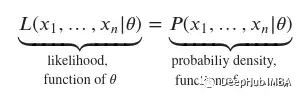
我们准备定义参数为𝜇和𝜎的高斯分布的似然函数:
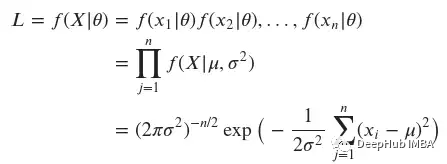
作为对似然函数有更多直观了解,我们可以生成足够多的样本来直观地了解它的形状。我们对从概率分布中生成样本不感兴趣,我们感兴趣的是生成参数𝜃,使观测数据的概率最大化,即𝑃(𝑥1,…,𝑥𝑛|𝜃)。
我们使用与上面相同的样本𝑥1=−0.5,𝑥2=0和𝑥3=1.5。
X
[-0.5, 0, 1.5]
为了能够构建2D可视化,我们可以创建一个潜在参数的网格,在一段时间间隔内均匀采样,𝜇从[-2,2]采样,𝜎从[0,3]采样。由于我们对每个参数采样了100个值,得到了𝑛^2个可能的组合。对于每个参数的组合,我们需要计算每个样本的概率并将它们相乘。
μ = np.linspace(-2, 2, 100)
σ = np.linspace(0, 3, 100)
l_x = []
for mu in μ:
for sigma in σ:
l_x.append(np.prod(tfd.Normal(mu, sigma).prob(X)))
l_x = np.asarray(l_x).reshape((100, 100)).T
现在准备绘制似然函数。注意这是观察到的样本的函数,这些是固定的,参数是我们的自变量。
plt.contourf(μ, σ, l_x)
plt.xlabel('μ')
plt.ylabel('σ')
plt.colorbar()
plt.title('Likelihood');
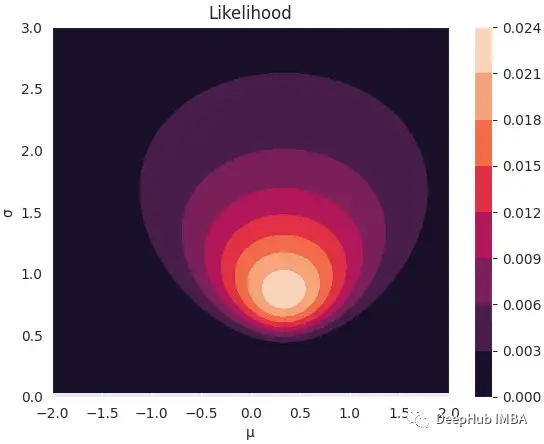
我们感兴趣的是最大化数据的概率。这意味着想要找到似然函数的最大值,这可以借助微积分来实现。函数的一阶导数对参数的零点应该足以帮助我们找到原函数的最大值。
但是,将许多小概率相乘在数值上是不稳定的。为了克服这个问题,可以使用同一函数的对数变换。自然对数是一个单调递增的函数,这意味着如果x轴上的值增加,y轴上的值也会增加。这很重要,因为它确保概率对数的最大值出现在与原始概率函数相同的点。它为我们做了另一件非常方便的事情,它将乘积转化为和。
让我们执行变换:
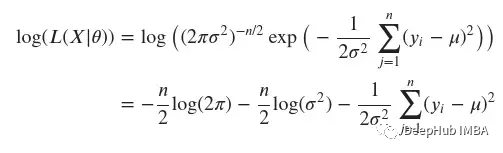
现在可以着手解决优化问题了。最大化我们数据的概率可以写成:
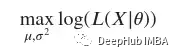
上面的表达式可以被求导以找到最大值。展开参数有log(𝐿(𝑋|𝜇,𝜎))。由于它是两个变量𝜇和𝜎的函数,使用偏导数来找到最大似然估计。
专注于𝜇´("撇"表示它是一个估计值,即我们的输出),我们可以使用以下方法计算它:
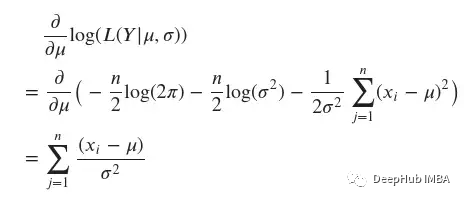
为了找到最大值,我们需要找到临界值,因此需要将上面的表达式设为零。
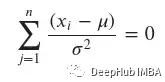
得到
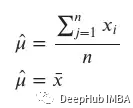
这是数据的平均值,可以为我们的样本𝑥1=−0.5,𝑥2=0和𝑥3=1.5计算μ和σ的最大值,并将它们与真实值进行比较。
idx_μ_max = np.argmax(l_x, axis=1)[-1]
print(f'μ True Value: {np.array(X).mean()}')
print(f'μ Calculated Value: {μ[idx_μ_max]}')
print(f'σ True Value: {np.array(X).std()}')
print(f'σ Calculated Value: {σ[np.nanargmax(l_x[:,idx_μ_max], axis=0)]}')
μ True Value: 0.3333333333333333
μ Calculated Value: 0.3434343434343434
σ True Value: 0.8498365855987975
σ Calculated Value: 0.8484848484848485
最大似然估计在TensorFlow Probability中的实现
我们先创建一个正态分布随机变量并从中取样。通过绘制随机变量的直方图,可以看到分布的形状。
x_train = np.random.normal(loc=1, scale=5, size=1000).astype('float32')[:, np.newaxis]
plt.hist(x_train, bins=50);
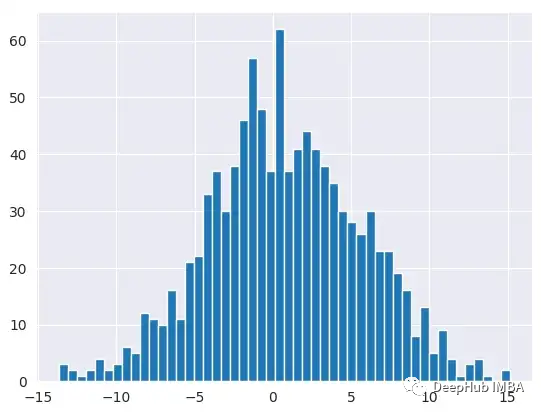
然后计算随机变量的均值,这是我们想用最大似然估计学习的值。
x_train.mean()
0.85486585
将TensorFlow Variable对象定义为分布的参数。这向TensorFlow说明,我们想在学习过程中学习这些参数。
normal = tfd.Normal(loc=tf.Variable(0., name='loc'), scale=5)
normal.trainable_variables
(<tf.Variable 'loc:0' shape=() dtype=float32, numpy=0.0>,)
下一步是定义损失函数。我们已经看到了我们想要达到的目标最大化似然函数的对数变换。但是在深度学习中,通常需要最小化损失函数,所以直接将似然函数的符号改为负。
def nll(x_train):
return -tf.reduce_sum(normal.log_prob(x_train))
最后建立训练程序,使用自定义训练循环,可以自己定义过程细节(即使用自定义损失函数)。
使用tf.GradientTape(),它是访问TensorFlow的自动微分特性的API。然后指定要训练的变量,最小化损失函数并应用梯度。
@tf.function
def get_loss_and_grads(x_train):
with tf.GradientTape() as tape:
tape.watch(normal.trainable_variables)
loss = nll(x_train)
grads = tape.gradient(loss, normal.trainable_variables)
return loss, grads
optimizer = tf.keras.optimizers.SGD(learning_rate=0.001)
现在训练程序已经准备完毕了。
@tf.function
def get_loss_and_grads(x_train):
with tf.GradientTape() as tape:
tape.watch(normal.trainable_variables)
loss = nll(x_train)
grads = tape.gradient(loss, normal.trainable_variables)
return loss, grads
optimizer = tf.keras.optimizers.SGD(learning_rate=0.001)
Step 000: Loss: 13768.004 Loc: 0.855
Step 001: Loss: 13768.004 Loc: 0.855
Step 002: Loss: 13768.004 Loc: 0.855
...
Step 1997: Loss: 13768.004 Loc: 0.855
Step 1998: Loss: 13768.004 Loc: 0.855
Step 1999: Loss: 13768.004 Loc: 0.855
我们通过最大化在第一时间生成的抽样数据的概率,计算了参数𝜇的最大似然估计。它是有效的,因为能够得到一个非常接近原始值的𝜇值。
print(f'True Value: {x_train.mean()}')
print(f'Estimated Value: {normal.trainable_variables[0].numpy()}')
True Value: 0.8548658490180969
Estimated Value: 0.8548658490180969
总结
本文介绍了最大似然估计的过程,和TensorFlow Probability的实现。通过一个简单的例子,我们对似然函数的形状有了一些直观的认识。最后通过定义一个TensorFlow变量、一个负对数似然函数并应用梯度,实现了一个使用TensorFlow Probability的自定义训练过程。
作者:Luís Roque