补一下第一次作业
第1关:数据输入与输出
第一题 在屏幕上输出字符串:hi, "how are you" ,I'm fine and you
第二题 从键盘输入两个整数,计算两个数相除的商与余数 假设输入12,5 输出为 2 2
第三题 在屏幕上 输入一个三位数输出该数的个位、十位和百位数字 假设输入125 输出为 5 2 1
第四题 已知a=1.234567,请按指定格式输出a的值1.按保留小数点后3位,2.指数形式,尾数部分保留小数点2位 ,输出格式:采用一行输出,中间用,隔开
第五题 请问一个硬盘的存储容量为500GB, 请问该硬盘最多可存放多少个字节的数据量 第六题 计算并判断(1.013)*(0.992)是否大于1.01,输出判断结果。可知“三天打鱼,两天晒网,终将一无所获”。
学习一下运算符号,‘+’、‘-’、‘*’、‘/’、‘//’取整、‘%’取模、‘**’幂、 '%.4f'%a 保留四位小数
#第一题:在屏幕上输出字符串:hi, "how are you" ,I'm fine and you
#-------begin-------------#
print ('hi, "how are you" ,I\'m fine and you')
#-------ends--------------#
#第二题:从键盘输入两个整数,计算两个数相除的商与余数
x,y = eval(input())
#-------begin-----------
print(x/y,x%y)
#第三题:在屏幕上输入一个三位数输出该数的个位、十位和百位数字
x = eval(input())
#-------begin-----------
a=x%10
b=(x//10)%10
c=x//100
print(a,b,c)
#-------ends------------
#第四题:已知a=1.234567,b=0.000321 .按保留小数点后3位输出a,2.按指数形式输出 b
a,b = 1.234567, 0.00321
#-------begin-----------
print("a="'%.3f'% a+","+"b=""{:.2e}".format(b))
#-------ends------------
#第五题:请问一个硬盘的存储容量为500GB, 请问该硬盘最多可存放多少个字节的数据量
#-------begin-----------
print(500*1024*1024*1024)
#-------ends------------
#第六题:计算并判断!,是否大于1.01,输出判断结果True,False。
#-------begin-----------
result = ((1.01**3)*((0.99)**2)) >= 1.01
print (result)
#-------ends------------
第2关:表达式的计算问题
第一题 分别计算并输出
π4+π5
、
e6
的值,以及二者的差。
第二题 分别计算
4π
与
4arctan(51)−arctan(2391)
的值,并观察其差异。
第三题 分别计算并输出
sinh(0.25)
与
2(e0.25−e−0.25)
的值,查看并比较二者的大小。
第四题 已知 h,v0,g,θ = 1.9, 14, 9.8, 40 #θ初始化为角度 计算并输出表达式的值 ,其中θ为弧度值。
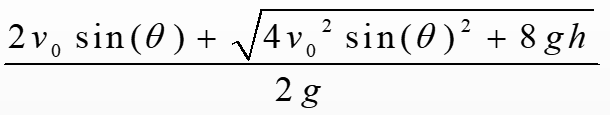
第五题 已知x为弧度数,从键盘输入 计算公式
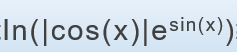
并输出结果 提示说明:也可以用exp(sin(x))函数求解
使用import math. 时引用函数要加上math. ;使用from math import *后后面引用函数时不加math.
注意弧度制与角度制的互换
#参考答案
from math import *
def print_(x):
if type(x) == float:
print("%.4f" % x)
else:
print(x)
# ********** Begin ********** #
#请在每一题的print语句内完成题目所需的表达式
#第一题
a = pow(pi,4)+pow(pi,5)
b = pow(e,6)
print_(a)
print_(b)
print_(a-b)
#第二题
print_(pi/4)
print_(4*atan(1/5)-atan(1/239))
#第三题
print_(sinh(0.25))
print_((exp(0.25)-exp(-0.25))/2)
#第四题
h,v0,g,θ = 1.9, 14, 9.8, 40 #变量赋值
θ=radians(θ)
print_((2*v0*sin(θ)+sqrt(4*(v0**2)*(sin(θ)**2)+8*g*h))/(2*g))
#第五题
θ = eval(input()) #输入角度值
θ = radians(θ)
print_(log(fabs(cos(θ))*exp(sin(θ)),e))
# ********** End ********** #
第3关:简单计算问题的求解
第一题:无输入求多边形的面积 计算一个由正方形和等腰三角形组成的多边形的面积,其中正方形边长 4 厘米,等腰三角形底边为正方形的一条边,其到对角顶点的高为 2.6 厘米。
第二题:根据公式
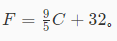
将摄氏温度转换为华氏温度,摄氏温度从键盘输入 例如输入:100 212.00 ####编程要求
第三题:钟形高斯函数如下所示,请在指定位置编写程序,计算不同参数下的结果。
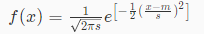
例如输入:0,2,1 #m,s,x分别赋值为0,2,1 输出:0.25
第四题:编写一个计算并打印地球上两点的大圆弧距离的Python程序。该程序接收用户的4个输入x1,y1,x2,y2 (分别表示地球上两个点的维度和经度,单位是度)。大圆弧距离计算公式为(单位是英里): 其中R=69.1105英里,1英里=1.609公里。请在指定位置编写程序,所给坐标之间的大圆弧距离,单位是公里。(注意,sin、cos函数输入是弧度值,而程序中给的是角度值,需要转换。arccos结果是弧度值,需要转化成角度值)。 仔细阅读右侧编辑区内给出的代码框架及注释,按照提示编写程序代码。 例如输入:48.87,-2.33,37.8,-122.4 输出:8716.97
还是那句话注意弧度角度互换
from math import *
def print_(x):
if type(x) == float:
print("%.2f" % x)
else:
print(x)
#第一题:无输入求多边形的面积
square_length = 4 # 声明整型变量square_length用于表示正方形边长,并赋值 4
triangle_h = 2.6 # 声明浮点型变量triangle_h用于表示三角形底边上的高,并赋值 2.6
# 请在下面的Begin-End之间按照注释中给出的提示编写正确的代码
########## Begin ##########
# 第1步:计算正方形面积,赋值给变量area_square
area_square = square_length*square_length
# 第2步:计算等腰三角形面积,赋值给变量area_triangle
area_triangle = square_length*triangle_h/2
# 第3步:计算多边形面积,即正方形面积和等腰三角形面积,赋值给变量area_total
area_total = area_square+area_triangle
# 第4步:打印输出多边形面积,即使用print_()函数输出变量area_total的值
print_(area_total)
########## End ##########
print('***********************')
#第二题:从键盘输入摄氏温度,将摄氏温度转换为华氏温度并输出
########## Begin ##########
#第1步:给C赋值
C = eval(input())
#第2步:计算F的值
F = (9/5*C+32)
########## End ##########
print_(F) #输出结果
print('***********************')
#第三题:钟形高斯函数的计算
########## Begin ##########
#第1步:给m,s,x赋值
m,s,x = eval(input())
#第2步:计算fx的值
fx = ((1/(sqrt(2*pi*s)))*exp(-1/2*pow((x-m)/s,2)))
########## End ##########
print_(fx) #输出结果
print('***********************')
#第四题:编写一个计算并打印地球上两点的大圆弧距离的Python程序
########## Begin ##########
#第1步:给x1,y1,x2,y2赋值
x1,y1,x2,y2 = eval(input())
#第2步:角度到弧度的转换
x1 = radians(x1)
y1 = radians(y1)
x2 = radians(x2)
y2 = radians(y2)
#第3步:计算dist的值
R=69.1105
d=acos(sin(x1)*sin(x2)+cos(x1)*cos(x2)*cos(y1-y2))
d= degrees(d)
dist=R*d*1.609
########## End ##########
print_(dist) #输出结果
print('***********************')
第4关:顺序程序设计
第一题:计算距离 一小球以 5 米/秒 的水平速度平抛,重力加速度取 9.8 米每秒的平方,在忽略空气阻力的情况下,求经过时间 t 秒后,小球所在位置与抛出点之间的距离 (假设小球距地面足够高)。 例如输入2 输出:22.00
第二题:求三角形面积 一个三角形的三边长分别是 a,b,c,那么它的面积为 sqrt(p(p−a)(p−b)(p−c)),其中 p= 1/2(a+b+c)。输入这三个数字,计算三角形的面积,四舍五入精确到 2 位小数。保证能构成三角形,0≤a,b,c≤1000,0≤a,b,c≤1000,每个边长输入时不超过2位小数。 例如输入:3,4,5 输出:6.00
第三题:逆序数输出 输入一个不小于 100 且小于 1000,同时包括小数点后一位的一个浮点数。 例如输入:123.4
输出:4.321
第四题: 对角线求点的个数 对于一个 n 个顶点的凸多边形,它的任何三条对角线都不会交于一点。请求出图形中对角线交点的个数。 例如:6 边形:结果为15个点 输入:6 输出:15
import math
def print_(x):
if type(x) == float:
print("%.2f" % x)
else:
print(x)
#**第一题**:计算距离
G = 9.8 # 声明浮点型变量 G,用于表示重力加速度
v0 = 5 # 声明整型变量 v0, 用于表示水平初速度
#请在下面的Begin-End之间按照注释中给出的提示编写正确的代码
########### Begin ###########
# 第一步:通过input函数获取输入值,将其转换为浮点型并赋值给t
t = eval(input())
t = float(t)
# 第二步:计算水平距离,并赋值给s
s = v0*t
# 第三步:计算垂直距离,并赋值给h
h = 1/2*G*math.pow(t,2)
# 第四步:计算小球与原点的距离,并赋值给d
d = math.sqrt((s**2)+(h**2))
# 第五步:按照保留小数点后2位格式输出小球与原点的距离d
print_(d)
########### End ###########
print('***********************')
#**第二题**:求三角形面积,结果保留小数点后2位
########### Begin ###########
#提供输入值
a,b,c = eval(input())
p = (a+b+c)/2
S = math.sqrt(p*(p-a)*(p-b)*(p-c))
print_(S)
########### End ###########
print('***********************')
#**第三题**:逆序数输出
########### Begin ###########
str_1 = input()
str_2 = str_1[-1]+str_1[-2]+str_1[-3]+str_1[-4]+str_1[-5]
float_1 = float(str_2)
print (float_1)
########### End ###########
print('***********************')
#**第四题**: 对角线求点的个数,以整数输出结果
########### Begin ###########
n = eval(input())
print (int(n*(n-1)*(n-2)*(n-3)/24))
########### End ###########
print('***********************')
版权归原作者 howell(Python) 所有, 如有侵权,请联系我们删除。