属性加密（ABE）基础知识

属性加密

最近在看ABE相关论文，因为本人（数学功底一般）不太能理解其中原理。所以特意记录ABE的基础知识，以便日后能快速重温。

ABE常见分类

属性基加密的思想是让密文和密钥与属性集合和访问结构产生关联，当且仅当属性集合满足访问结构的时候，方能解密成功。那么根据这其中两两的对应关系，又可以将属性基加密分为两类，即密钥策略属性基加密（KP-ABE）和密文策略属性基加密（CP-ABE）。

• KP-ABE：用户的密钥中蕴含访问结构（访问策略），密文中对应着一系列属性集合，当且仅当密文的属性集合满足用户密钥的访问结构时，用户才能解密成功。
• CP-ABE: 用户的密钥对应着一系列属性的集合，密文中蕴含着访问结构（策略），当且仅当用户的属性集合满足密文的访问结构时，用户才能解密成功。

下图为采用ABE的数据服务机构与其他实体的基本关系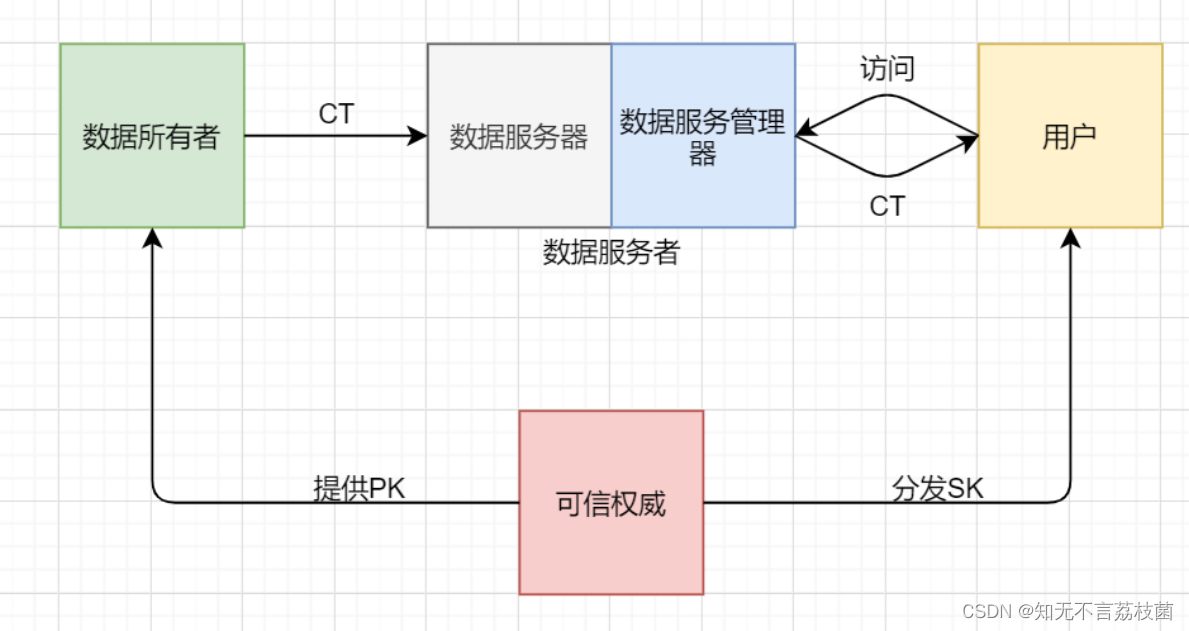

其实ABE中的CP-ABE十分适合构建云环境中数据安全共享方案。CP-ABE中数据拥有者（加密明文得到密文的人）可以根据自己的需求，定义合适的访问结构，让他所期待的一群用户能够解密。

而ABE采用主密钥+属性密钥的形式，是为了方便加密的外包以及撤销；而撤销是为了是为了设置有效期，实现更完善的访问控制。

双线性映射

双线性映射是基于Diffie-Hellman难题构建属性基加密算法的数学基础，此处的模糊身份基加密也用到了该数学基础。

令G1,G2为两个阶为p的乘法循环群，g为G1的生成元，一个从G1到G2的映射e:G1×G1→G2是双线性的，当其满足以下三点：
双线性：∀g,h∈G1和a,b∈Zp有e(ga,hb)=e(g,h)ab；
非退化性：e(g,h)≠1；
可计算性：∀g,h∈G1，存在有效的算法计算e(g,h)∈G2。

相关概念：

合数阶群双线性映射

素数阶群双线性映射

补充
若G1≠G2，称该映射为 非对称双线性映射
若G1=G2，称该映射为 对称双线性映射

单调访问结构

例如：假设有用户{1,2,3,4},只有 (1,2) 合作，或者 (3,4) 合作可以恢复秘密，(1,3,4) 当然也可以恢复秘密，但是 (1,3,4) 不是 ((1,2),(3,4)) 的超集。

• 可以理解为在包含所需要的属性的基础上，包含的属性更多，也依然符合这一访问结构。（即为授权集合）

与门访问结构（And-Gate）

访问控制树（Access Tree）

访问树是一种用于隐藏源数据密钥的结构。只有符合访问树的条件，才能解出其中的秘密值。访问树是由根节点、非叶节点、叶节点构成的。访问树的节点很独特，举一个简单的例子。假设访问树T有一节点x，子节点数就记为num_x,阈值记为k_x。当x不是叶子节点，那么x在树中就表示为阈值关系（由num_x和k_x决定）。当x是叶节点时，则会代表一个属性att（显然num_x为0，k为1）。

• 阈值关系：num_x = x_k即“AND”；x_k<num_x即“num_x个子节点需要满足x_k个的门限关系”，注意x_k=1时即为“OR”。

构造访问树

假设现有一份共享数据，只有当访问者满足以下要求时才能访问：
1.网络实验室或云实验室的老师
2.计算机学院研二的硕士且属于网络或云实验室

首先根据上述条件构建访问树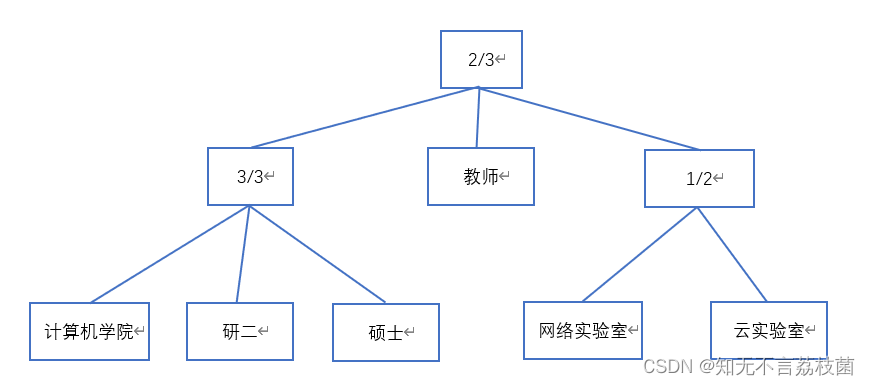

访问树构造好了，我们怎么隐藏秘密呢？

秘密值生成

秘密值的生成，一般是由随机生成的。以上图为例，从根节点开始，孩子节点有3个，随机生成一个多项式，其最高次数为k_x-1，故根节点的最高次数为1，然后将常数项设置为秘密数（秘密数为需要秘密保存的数）；如此根节点随机的多项式为f(x)=5+3x，秘密数为5。此外，将根节点的孩子节点从左至右依次标记为1,2,3,…，将节点标记值代入f(x)函数中，所得值（即生成新的秘密值）传给该标记的孩子节点秘密保存；故“3/3”节点（左边第一个节点）标记为1，传给“3/3”节点的秘密值f(1)=5+31=8，中间“教师”节点（中间节点）标记为2，传给“教师”节点的秘密值f(2)=5+32=11，“1/2”节点（右边节点）标记为3，传给“1/2”节点的秘密值为f(3)=5+3*3=14。

“3/3”节点和“1/2”节点在接收到父节点传来的值后，按照上述方式生成随机多项式，将常数项设置为父节点传来的值，此外也按照上述方式生成新的秘密值并将它传给子节点，数据如图所示（对于非叶子节点，都按照此方式进行）。对于叶子节点，在接受到父节点的秘密值后，用此叶子节点的属性对秘密值进行加密处理。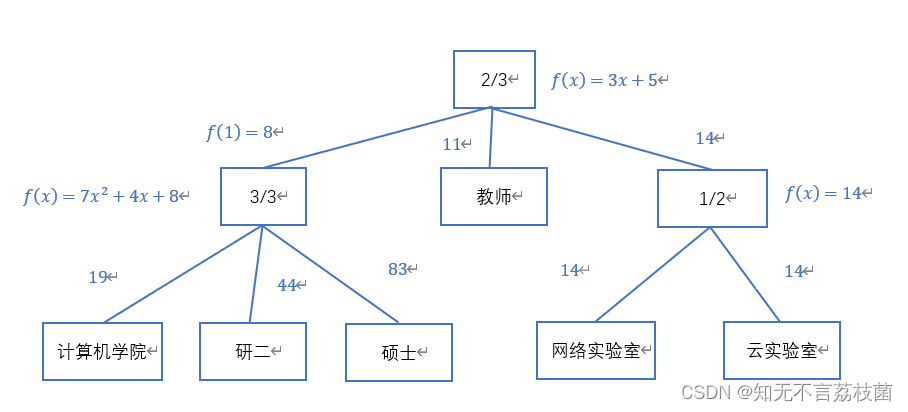

解密访问树

当数据访问者满足访问树，则可以通过获取属性中存放的秘密值。然后就可以用拉格朗日公式（后面有讲解，略过）解出父节点生成多项式的常数项。自下而上，最终可以解出根节点中的常数项，即访问树中隐藏的秘密值。

线性秘密共享（LSSS）

• 本质还是矩阵运算。

离散对数难题

令α∈Zp，G为一个乘法循环群，群的阶数为p，群的一个生成元为g，离散对数难题说的是：给定g,ga∈G，对于任何多项式时间的攻击者，其计算出指数a的概率是可忽略的，即由g,ga∈G计算出a是困难的。

拉格朗日插值法

辅助理解：视频

安全模型（安全游戏/挑战）

按照攻击者能力划分：选择明文攻击、选择密文攻击、适应性/非适应性选择密文攻击

按照安全目标划分：单向安全性、不可区分安全性、非延展安全性
模糊身份基加密中是选择身份模型（selective-ID），而属性基加密中是选择集合模型（selective-set）。而且上述模型有两个地方需要注意：

在CP-ABE模型没有Init阶段（在模糊身份基加密的模型中有init阶段），称之为选择明文攻击下不可区分安全（IND-CPA）。如果在Init阶段攻击者声明想要挑战的访问结构，则称之为选择安全模型。很显然，选择安全模型描述的安全性弱一些。

若是在Phase 1阶段还适应性地查询密文，则称之为适应性选择密文攻击安全模型1（CCA1），若是继续在Phase 2阶段还适应性地查询密文，则称之为适应性选择密文攻击安全模型2（CCA2)。很显然，就安全性而言，IND-CPA、CCA1、CCA2依次增强。

安全性证明

• 安全性证明定义：密码算法中安全性证明就是判定在一个普通的攻击模型中，密码算法和所依赖的可信密码学算法问题之间的规约关系，如果算法的攻破（即攻击者赢）意味着某一在密码学中可信问题的解决，则说明该算法是安全的，即安全性得到证明。

密码学中构建方案，通常将方案的安全性规约到某个数学困难问题，用反证法的思想，当难题是困难的，那么攻破方案就是困难的。FIBE方案是在选择身份模型下将方案规约到MBDH问题。（除此之外还有DL、BDH、DBDH等安全假设）。

Waters论文中详细介绍了三种具体方案的构造，但是前两种被学者们“开发”的多，因此在这里着重介绍前两种。第一种基于Decisional q-PBDHE困难假设，第二种基于BDHE假设。无论是哪一种构造，方案的安全模型是和CP-ABE里边的安全模型是一样的。这些实现都将线性秘密共享（LSSS） 作为访问结构，进而依赖特定的难题，完成安全性的规约证明。

可证明安全理论

1. 无条件安全性：这种评价方法考虑的是假定攻击者拥有无限的计算资源，但仍然无法破译该密码系统
2. 计算安全性：这种方法是指使用目前最好的方法攻破它所需要的计算远远超出攻击者的计算资源水平，则可以定义这个密码体制是安全的。
3. 可证明安全性 这种方法是将密码系统的安全性归结为某个经过深入研究的数学难题（如大整数素因子分解、计算离散对数等），数学难题被证明求解困难。这种评估方法存在的问题是它只说明了这个密码方法的安全性与某个困难问题相关，没有完全证明问题本身的安全性，并给出它们的等价性证明。

对于实际应用中的密码系统而言，由于至少存在一种破译方法，即强力攻击法，因此都不能满足无条件安全性，只提供计算安全性。密码系统要达到实际安全性，就要满足以下准则：

• 破译该密码系统的实际计算量（包括计算时间或费用）十分巨大，以致于在实际上是无法实现的。
• 破译该密码系统所需要的计算时间超过被加密信息有用的生命周期。例如，战争中发起战斗攻击的作战命令只需要在战斗打响前需要保密；重要新闻消息在公开报道前需要保密的时间往往也只有几个小时。
• 破译该密码系统的费用超过被加密信息本身的价值。 如果一个密码系统能够满足以上准则之一，就可以认为是满足实际安全性的。

参考文章

属性集加密基础知识
可证明安全理论总结