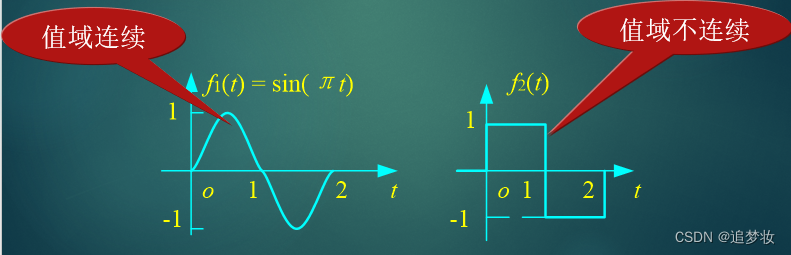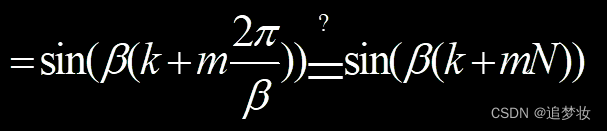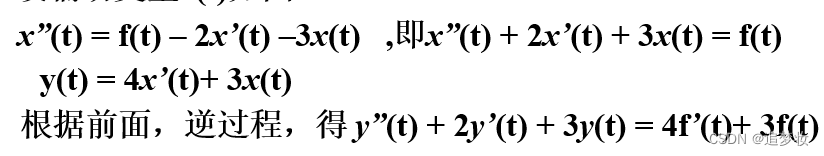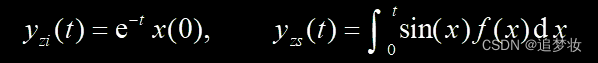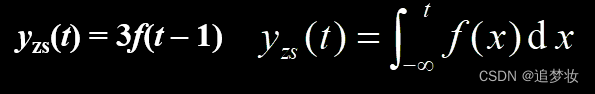本文章内容来源于书本、课件与自己的理解。
1.1 绪论
1.1.1 信号
信号理论包括:信号分析、信号传输、信号处理和信号综合。
定义:信号是信息的一种物理体现。它一般是随时间或位置变化的物理量(函数)。
信号是系统处理的对象和产物。
信号是信息的一种表示方式,通过信号传递信息。
描述信号的常用方法(信号可以用函数、图形来表示。):(1)表示为时间的函数(2)信号的图形表示——波形
“信号”与“函数”两词常相互通用。
信号按物理属性分:电信号和非电信号。它们可以相互转换。
电信号容易产生,便于控制,易于处理。本课程讨论电信号,简称“信号”。
电信号的基本形式:随时间变化的电压或电流。
1.1.2 系统
系统理论包括系统分析和系统综合。
信号的产生、传输和处理需要一定的物理装置,这样的物理装置常称为系统。
定义:一般而言,系统(system)是指若干相互关联相互作用的事物按照一定规律组合而成的具有特定功能的整体。
不同系统有着不同的属性和规律。
1.1.3 信号与系统的关系
信号是系统处理的对象和产物。
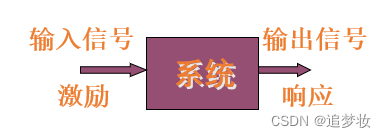
一般只关心“输入”与“输出”的关系(即输入信号与输出信号的关系,与系统无关)
信号分析主要讨论信号的表示、信号的性质等,侧重于信号的解析表示、性质、特征等;系统分析主要研究对于给定的系统(它也是信号的变换器或处理器),在输入信号(激励)的作用下产生的输出信号(相应),着眼于系统的特性、功能等。信号分析和系统分析是信号传输、信号处理、信号综合及系统综合的共同理论基础。
系统是信号产生、传输和处理(加工、分析)的物理装置。
信号处理
定义:对信号进行某种加工或变换。
目的:消除信号中的多余内容;滤除混杂的噪声和干扰;将信号变换成容易分析与识别的形式,便于估计和选择它的特征参量。
1.2 信号
1.2.1 信号的描述(见本章的“1.1信号”)
1.2.2 信号的分类
信号的分类方法很多,可以从不同的角度对信号进行分类。
按实际用途划分:电视信号,雷达信号,控制信号,通信信号,广播信号,……
按所具有的时间特性划分:
1.2.2.1 确定信号和随机信号
确定性信号
可用确定的时间函数表示的信号。对于指定的某一时刻t,有确定的函数值f(t)。
随机信号
取值具有不确定性的信号。
“不确定性”或“不可预知性”统称为随机性。
在实践中经常遇到的信号一般都是随机信号,如:电子系统中的起伏热噪声、雷电干扰信号。
虽然随机,但是依旧会有统计规律。
1.2.2.2 连续信号和离散信号(重点)
连续时间信号
在连续的时间范围内(-∞< t <∞)有定义的信号称为连续时间信号,简称连续信号。
这里的“连续”指函数的定义域—时间是连续的,但可含间断点,至于值域可连续也可不连续。 用t表示连续时间变量。
注意区分连续信号与连续函数
两幅图都表示连续信号,因为在一定时间t内都是连续的;
左边的是连续函数,右边的不是连续函数,他们的区别是值域是否连续。
离散时间信号
仅在一些离散的瞬间才有定义(即其他瞬间没有定义)的信号称为离散时间信号,简称离散信号。
这里的“离散”是指定义域——时间是离散的,它只在某些规定的离散瞬间给出函数值,其余时间无定义。f(t)仅在一些离散时刻t(k)(k = 0,±1,±2,…)才有定义,其余时间无定义。
离散点间隔T(k)= t(k+1)-t(k)可以相等也可不等(即离散的瞬间可均匀,也可不均匀)。通常取等间隔T,离散信号可表示为f(kT),简写为f(k),这种等间隔的离散信号也常称为序列。其中k称为序号,是整数。
描述离散信号可以用公式列举、写为集合(通常将对应某序号m的序列值称为第m个样点的“样值”)。
1.2.2.3 周期信号和非周期信号
周期信号
定义在**(-∞,∞)区间,每隔一定时间T (或整数N),按相同规律重复变化的信号。
连续周期信号f(t)满足 f(t) = f(t + mT),m = 0,±1,±2,…
离散周期信号f(k)满足 f(k) = f(k + mN),m = 0,±1,±2,…
满足上述关系的最小T(或整数N)称为该信号的周期。
两个周期信号x(t),y(t)的周期分别为T1和T2,若其周期之比T=T1/T2为有理数,则其和信号x(t)+y(t)仍然是周期信号,其周期T为T1和T2的最小公倍数。
其中,T=T1和T2的最小公倍数=T1与T2分子的最小公倍数÷T1与T2分母的最大公约数**
非周期信号
不具有周期性的信号称为非周期信号。
当计算出来的周期T为无理数时,该信号为无周期信号。
连续周期信号举例
例 判断下列信号是否为周期信号,若是,确定其周期。
(1)f1(t) = sin2t + cos3t
(2)f2(t) = cos2t + sinπt
分析 两个周期信号x(t),y(t)的周期分别为T1和T2,若其周期之比T1/T2为有理数,则其和信号x(t)+y(t)仍然是周期信号,其周期T为T1和T2的最小公倍数;若其周期之比T1/T2为无理数,则其和信号x(t)+y(t)是非周期信号。解答
(1)sin2t 是周期信号,其角频率和周期分别为 ω1= 2 rad/s , T1= 2π/ ω1= πs
cos3t是周期信号,其角频率和周期分别为 ω2= 3 rad/s , T2= 2π/ ω2= (2π/3) s
由于T1/T2= 3/2为有理数,故f1(t)为周期信号,其周期为T1和T2的最小公倍数2π。
(2) cos2t 和sinπt的周期分别为T1= πs, T2= 2 s,由于T1/T2为无理数,故f2(t)为非周期信号。
离散周期信号举例1(考点)
例 判断正弦序列f(k) = sin(βk)是否为周期信号,若是,确定其周期。
解 f (k) = sin(βk) = sin(βk + 2mπ) , m = 0,±1,±2,…式中β称为数字角频率,单位:rad。
因为离散周期信号f(k)满足 f(k) = f(k + mN),m = 0,±1,±2,…由上式可见:
仅当2π/ β为整数时,正弦序列才具有周期N = 2π/ β。
当2π/ β为有理数时,正弦序列仍为具有周期性,但其周期为N= M(2π/ β),M取使N为整数的最小整数。
当2π/ β为无理数时,正弦序列为非周期序列。
离散周期信号举例2
例 判断下列序列是否为周期信号,若是,确定其周期。
(1)f1(k) = sin(3πk/4) + cos(0.5πk)
(2)f2(k) = sin(2k)
解 (1)sin(3πk/4) 和cos(0.5πk)的数字角频率分别为 β1 = 3π/4 rad, β2 = 0.5π rad
由于2π/ β1 = 8/3, 2π/ β2 = 4为有理数,故它们的周期分别为N1 = 8 , N2 = 4,故f1(k) 为周期序列,其周期为N1和N2的最小公倍数8。
(2)sin(2k) 的数字角频率为 β1 = 2 rad;由于2π/ β1 = π为无理数,故f2(k) = sin(2k)为非周期序列 。原理与上面的“连续周期信号举例”类似,但是注意对于离散信号来说,想要序列是周期信号,每个三角函数的周期都不能为无理数,即2π/ β不能为无理数。
总结
①连续正弦信号一定是周期信号,而正弦序列不一定是周期序列(因为周期可能是含有π的无理数)。
②两连续周期信号之和不一定是周期信号(连续周期信号的周期中可能含有π这样的无理数,这样的话两个之和就不是周期信号了),而两周期序列之和一定是周期序列。
1.2.2.4 实信号与复信号
实信号
时间t(或k)的实函数(或序列),其在各时刻的函数(或序列)值为实数,例如单边指数函数、正弦函数等,称为实信号。
复信号
函数(或序列)值为复数的信号称为复信号,最常用的是复指数信号。
1.2.2.5 能量信号与功率信号
信号(电压或电流)在单位电阻上的能量或者功率,亦称为归一化能量或功率。
将信号f (t)施加于1Ω电阻上,它所消耗的瞬时功率为| f (t) |^2
在区间(–∞ , ∞)的能量和平均功率定义为:
信号的能量E
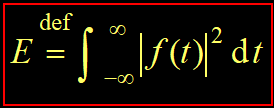
信号的功率P

若信号f (t)的能量有界,即 E <∞ ,则称其为能量有限信号,简称能量信号。此时 P = 0
若信号f (t)的功率有界,即 P <∞ ,则称其为功率有限信号,简称功率信号。此时** E = ∞**
离散信号的功率和能量
满足以下条件的离散信号,称为能量信号
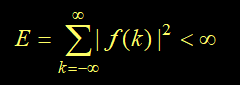
满足以下条件的离散信号,称为功率信号
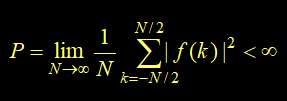
一般规律
一般周期信号为功率信号。
时限信号(仅在有限时间区间不为零的非周期信号)为能量信号。
还有一些非周期信号,也是非能量信号(同时不满足)。
如ε(t)是功率信号;而tε(t)、 e^t为非功率非能量信号;
1.2.2.6 一维信号与多维信号
一维信号
只由一个自变量描述的信号,如语音信号。
多维信号
由多个自变量描述的信号,如图像信号。
1.2.2.7 因果信号与反因果信号
因果信号:满足在t<0时,f(t)=0
反因果信号:满足在t>0时,f(t)=0
非因果信号:满足在t<0时,f(t)≠0
1.2.3 几种典型确定性信号
1.2.3.1 指数信号
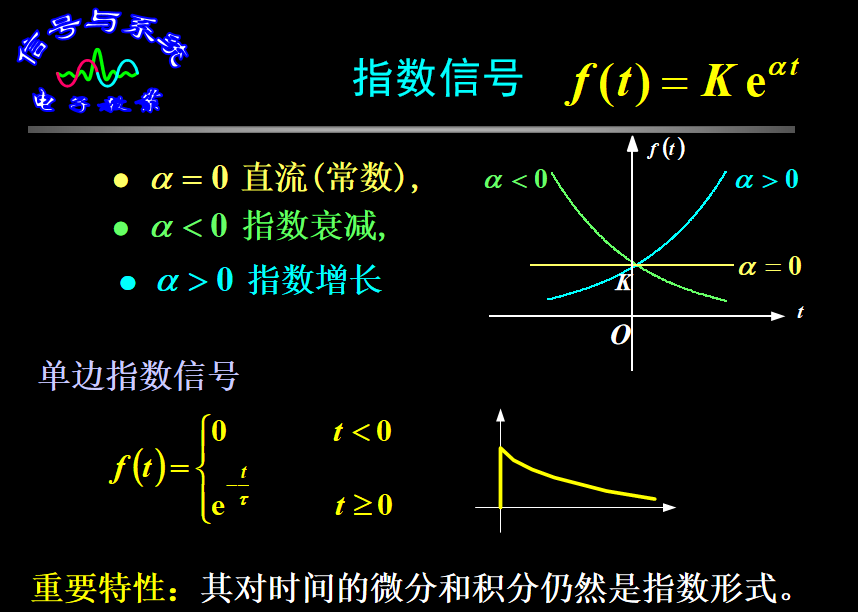
1.2.3.2 正弦信号

1.2.3.3 复指数信号(表达具有普遍意义)

1.2.3.4 抽样信号(Sampling Signal)
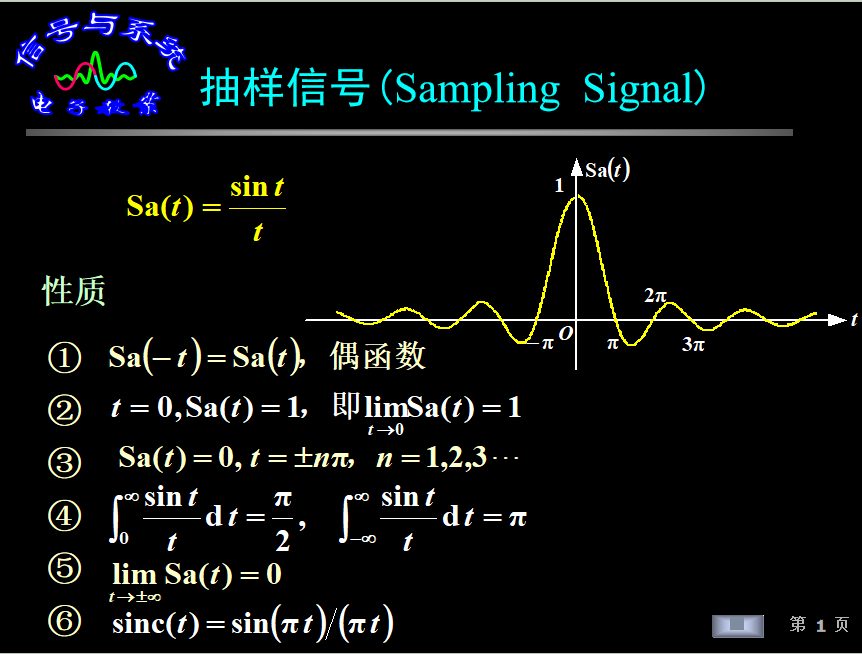
1.3 信号的基本运算
1.3.1 两信号相加或相乘
两信号之和(瞬间和)是指同一瞬间两信号之值对应相加所构成的“和信号”
两信号之积(瞬间积)是指同一瞬间两信号之值对应相乘所构成的“积信号”
连续信号相加、乘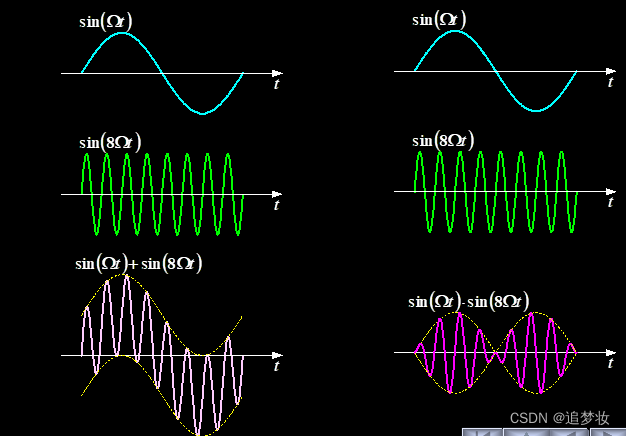
离散序列相加、乘
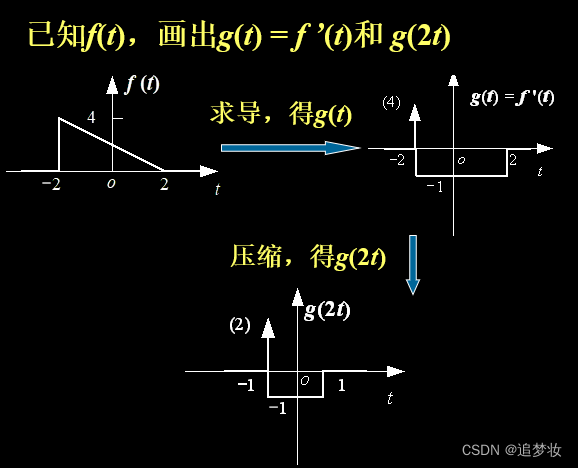
1.3.2 信号的时间变换
1.3.2.1 反转
将 f (t) → f (– t) , f (k) → f (– k) 称为对信号f (·)的反转或反折。
从图形上看是将f (·)以纵坐标为轴反转180°。
没有可实现此功能的实际器件。数字信号处理中可以实现此概念,例如堆栈中的“后进先出”。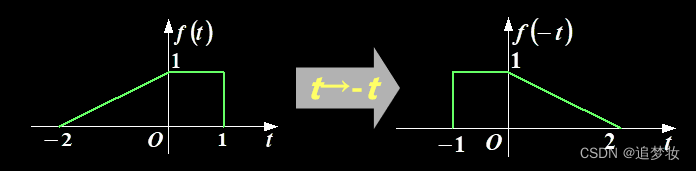
1.3.2.2 平移
将 f (t) → f (t – t0) , f (k) → f (t – k0)称为对信号f (·)的平移或移位。
若t0 (或k0) >0,则将f (·)右移;否则左移。
雷达接收到的目标回波信号就是平移信号。
同时,需要注意因果信号的平移,可能存在两种情况:
(1)因果信号的右移
(2)双边信号右移的因果部分
例如,f(t)=tε(t),则对于(1)来说,结果为f(t-t0)=(t-t0)ε(t-t0),这个也是最常用的因果信号的平移;对于(2)来说,结果为(t-t0)ε(t)。
1.3.2.3 展缩(尺度变换)
将 f (t) → f (a t) , 称为对信号f (t)的尺度变换。若a >1 ,则波形沿横坐标压缩;若0< a < 1 ,则扩展(书上为展宽),即横坐标变化为原来的1/a、
对于离散信号,由于 f (a k) 仅在为a k 为整数时才有意义, 进行尺度变换时可能会使部分信号丢失。因此一般不作波形的尺度变换。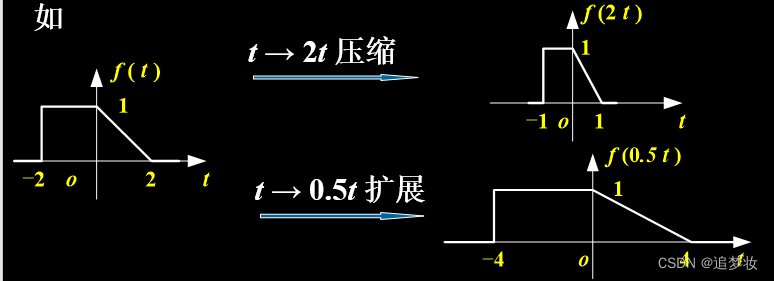
1.3.2.4 综合例题
平移与反转相结合举例
**例 **已知f (t)如图所示
,画出 f (2 – t)。
解答
法一:①先平移f (t) → f (t +2) ②再反转 f (t +2) → f (– t +2)
法二:①先反转 f (t) → f (– t) ②再平移 f (– t) → f (– t +2)注意:平移的顺序与方向,一般情况下可以根据某个点来确定
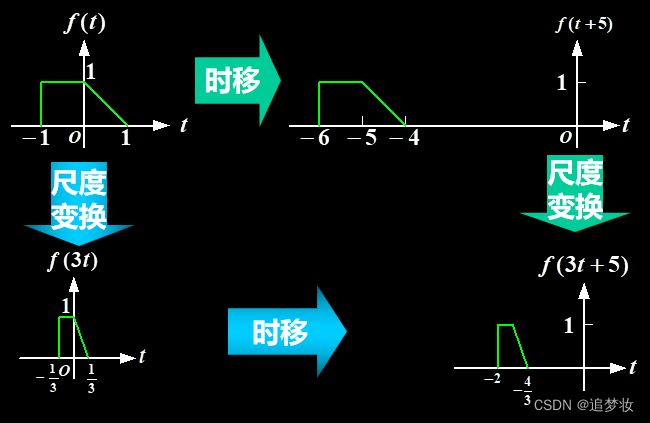
平移与尺度变换相结合举例
例 已知f (t)如图所示
,画出 f (3t + 5)。
解答
法一(常用):①先平移f (t) → f (t +5) ②再尺度变换 f (t +5) → f (3t +5)
法二:①先尺度变换 f (t) → f (3t) ②再平移 f (3t) →f[3(t+5/3)] = f (3t +5)注意:平移的顺序、方向与大小,尺度变换的顺序,一般情况下可以根据某个点来确定
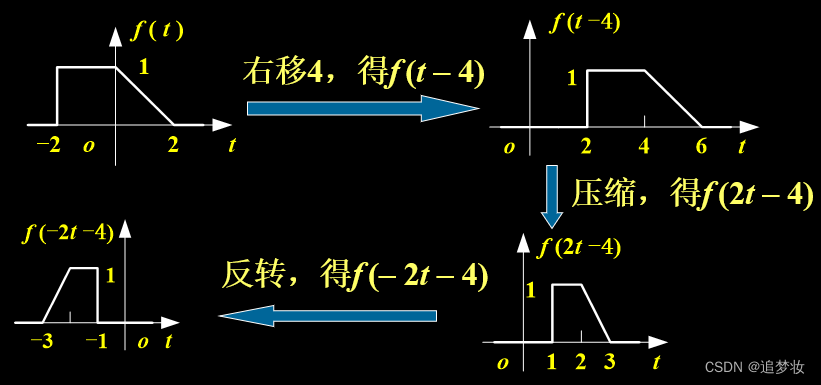
平移、反转、尺度变换相结合,正逆运算举例
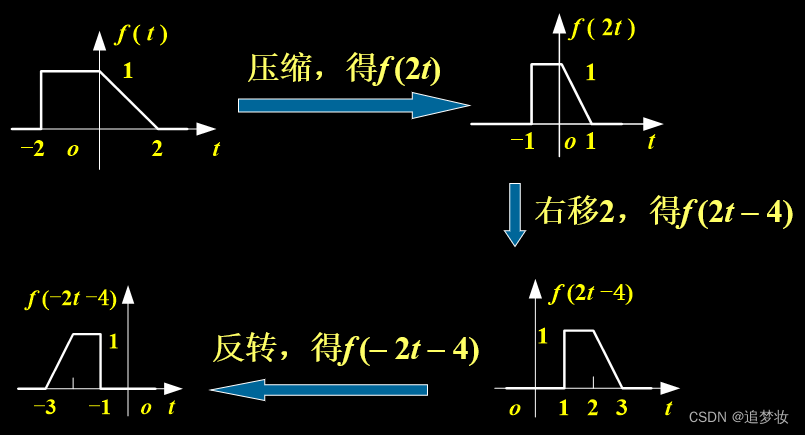
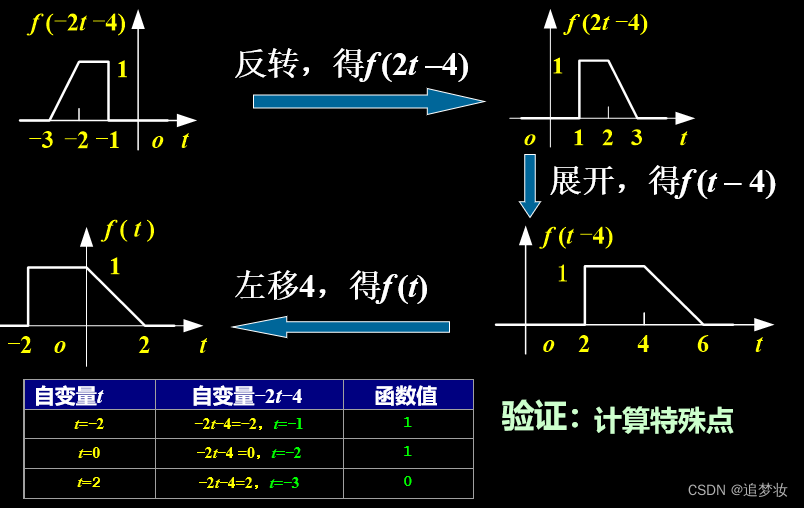
例 已知f (t)如图所示
,画出 f (- 2t - 4)。
解答
法一(常用):先平移,再压缩,最后反转
法二:先压缩,再平移,最后反转
补充 若已知f (– 4 – 2t) ,画出 f (t) 。
1.3.2.5 总结
混合运算时,三种运算的次序可任意。但一定要注意一切变换都是相对t 而言。
通常,对正向运算,先平移,后反转和展缩不易出错;对逆运算,反之。
1.3.3 信号的微分和积分

1.4 阶跃函数和冲激函数
函数本身有不连续点(跳变点)或其导数与积分有不连续点的一类函数统称为奇异信号或奇异函数。(因为“信号”与“函数”可以相互转化)
阶跃函数和冲激函数是两个典型的奇异函数。
1.4.1 单位阶跃函数
1.4.1.1 定义
下面采用求函数序列极限的方法定义阶跃函数。(将那个函数序列的n不断扩大,即曲线的斜率越来越大,最后成为阶跃函数)

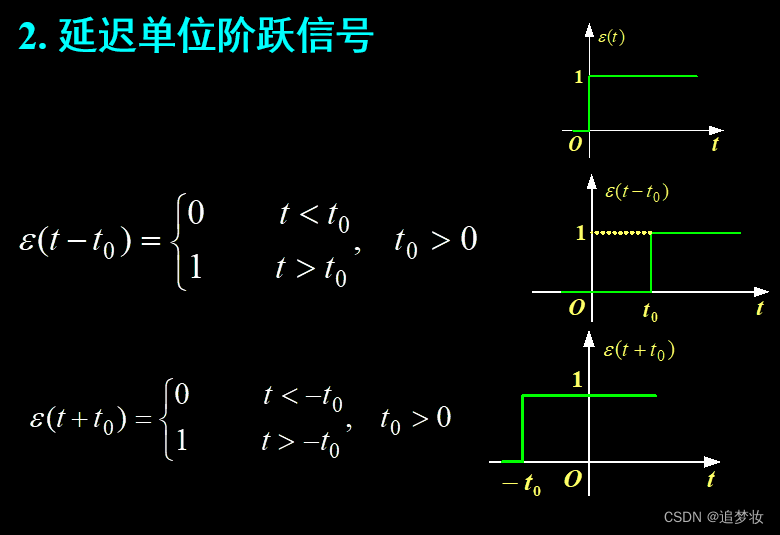
1.4.1.2 延迟单位阶跃信号
1.4.1.3 阶跃函数的性质
(1)可以方便地表示某些信号
(2)用阶跃函数表示信号的作用区间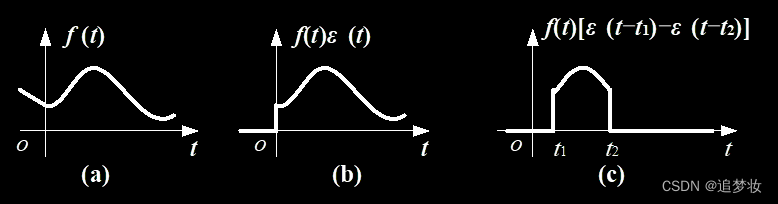
(3)积分
1.4.2 单位冲激函数
单位冲激函数是个奇异函数,它是对强度极大,作用时间极短一种物理量的理想化模型。
1.4.2.1 狄拉克(Dirac)定义
定义:(1)函数值只在t = 0时不为零;(2)积分面积为1;(3)t =0时,δ(t)→∞,为无界函数。
公式: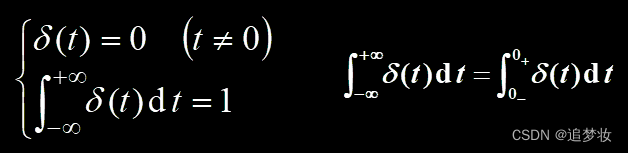
图示:
1.4.2.2 函数序列定义δ(t)

1.4.2.3 冲激函数与阶跃函数关系
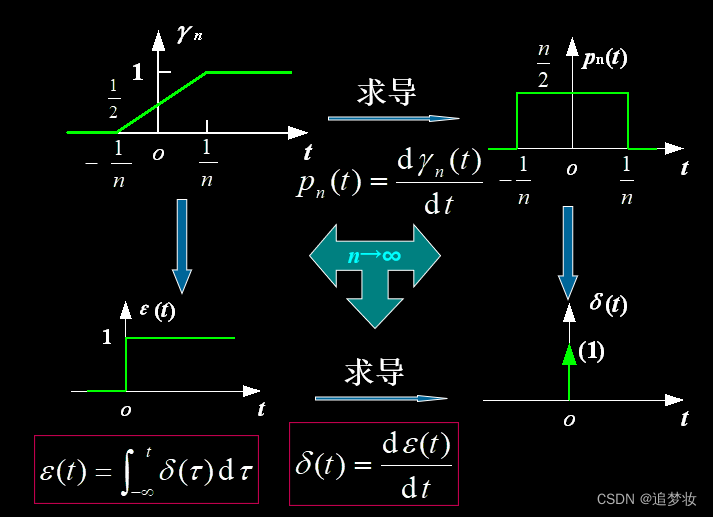
引入冲激函数之后,间断点的导数也存在
1.4.2.4 冲激函数的性质
1.取样性(筛选性)
定义:(注意:**没有使用积分时不能消去δ(t)**,否则存在问题)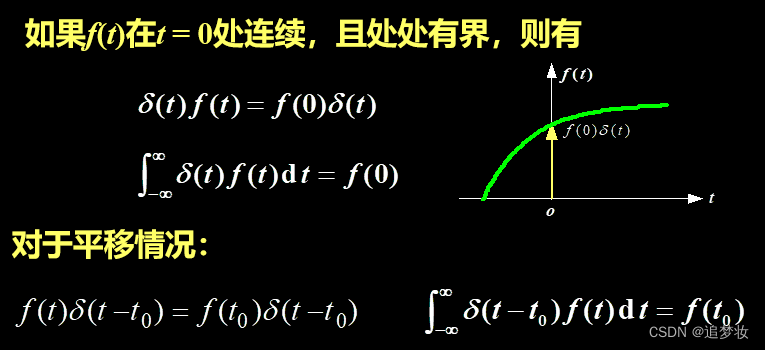
证明

举例
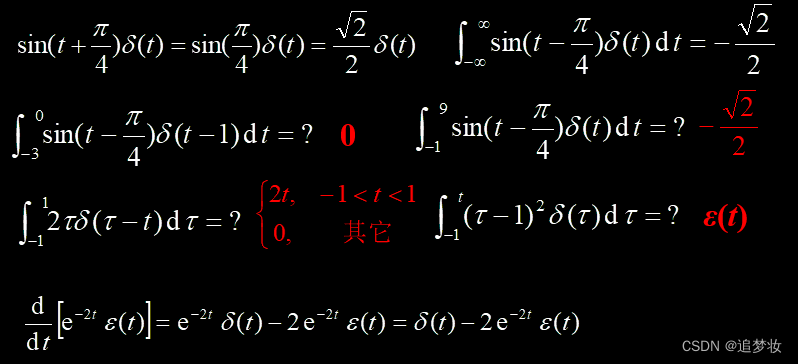
2.冲激偶
图示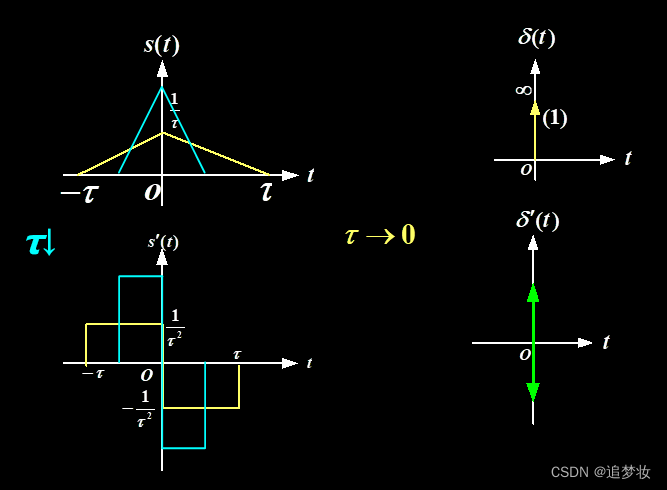
冲激偶的性质
冲激偶取样性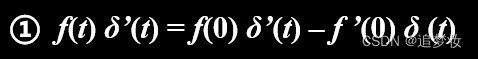
证明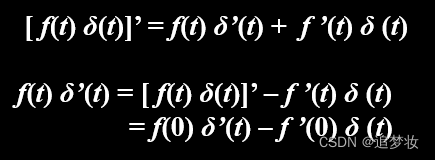
冲激偶积分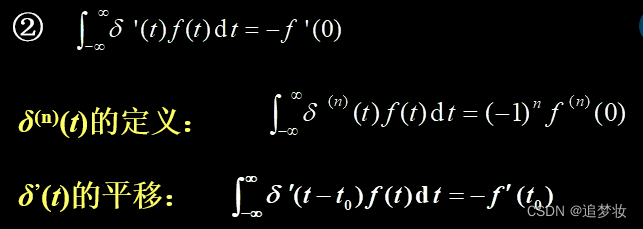
证明(利用分部积分运算)
冲激偶积分与例题
3.尺度变换
性质

冲激信号尺度变换的证明

冲激信号尺度变换举例
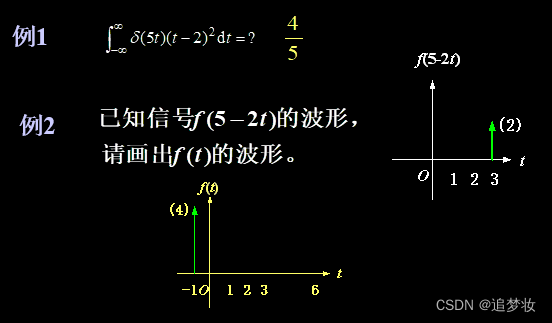
举例
4.复合函数形式的冲激函数
性质
实际中有时会遇到形如δ[f(t)]的冲激函数,其中f(t)是普通函数。并且f(t) = 0有n个互不相等的实根 ti ( i=1,2,…,n) 
举例
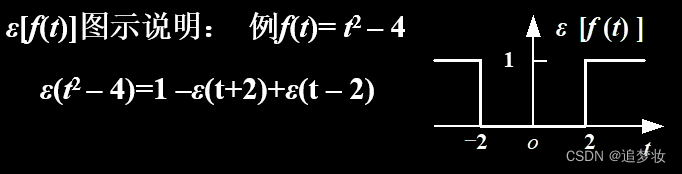

注意:如果f(t)=0有重根,δ[f(t)]无意义。
冲激函数的性质总结

1.4.3 序列δ(k)和ε(k)
这两个序列是普通序列。
1.4.3.1 单位(样值)序列δ(k)

1.4.3.2 单位阶跃序列ε(k)

1.5 系统的描述
1.5.1 前言
要分析一个系统,首先要建立描述该系统基本特性的数学模型,然后用数学方法(或计算机仿真)求出它的解答,并对所得结果赋予实际含义。
按数学模型的不同,系统可分为:即时系统与动态系统;连续系统与离散系统;线性系统与非线性系统;时变系统与时不变(非时变)系统等。
1.5.2 系统的数学模型:系统物理特性的数学抽象。
1.5.2.1 连续系统解析描述:微分方程
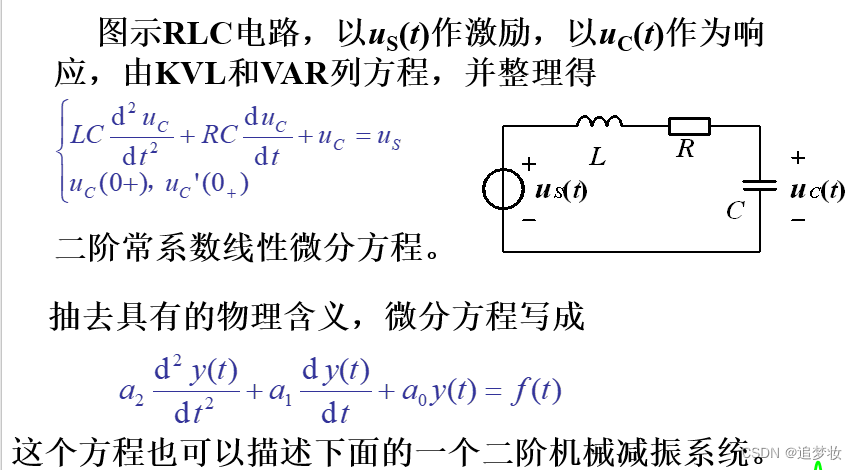
1.5.2.2 离散系统解析描述:差分方程

描述LTI系统的是线性常系数差分方程
**例 **下列差分方程描述的系统,是否线性?是否时不变?并写出方程的阶数。
(1)y(k) + (k – 1)y(k – 1) = f(k)
(2) y(k) + y(k+1) y(k – 1) = f2(k)
(3) y(k) + 2 y(k – 1) = f(1 – k)+1
分析判断方法:方程中均为输出、输入序列的一次关系项,则是线性的。输入输出序列前的系数为常数,且无反转、展缩变换,则为时不变的。
解(1)线性、时变,一阶
(2)非线性、时不变,二阶
(3)非线性、时变,一阶
1.5.3 系统的框图表示:形象地表示其功能。
1.5.3.1 前言
上述方程从数学角度来说代表了某些运算关系:相乘、微分(差分)、相加运算。
将这些基本运算用一些基本单元符号表示出来并相互联接表征上述方程的运算关系,这样画出的图称为模拟框图,简称框图。
框图为计算关系图,电路图为连接图
一个方框(或其他形状)可以表示一个具有某种功能的部件,也可表示一个子系统。
每个方框内部的具体结构并非考察重点,而只注重其输入、输出之间的关系。
1.5.3.2 连续系统的基本单元
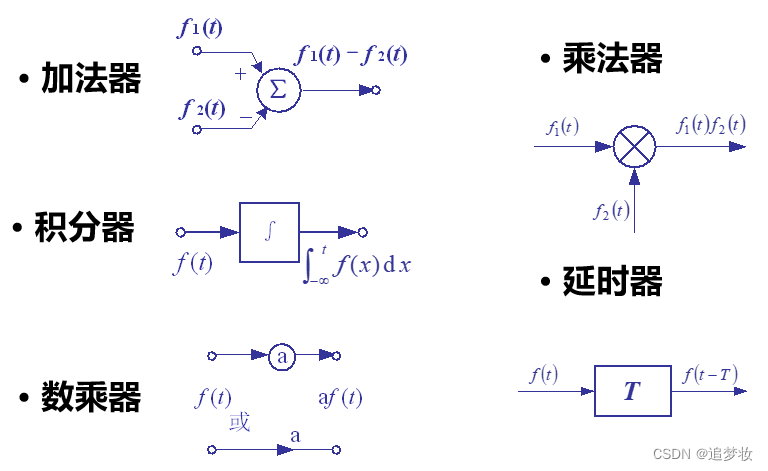
没有微分器,它用积分器表示,因为积分器的抗干扰能力强
1.5.3.3 离散系统的基本单元(加法器、迟延单元、数乘器)
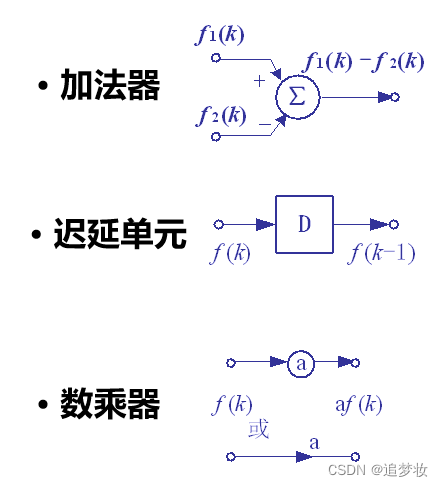
1.5.3.4 系统模拟
实际系统→方程→模拟框图→实验室实现(模拟系统)→指导实际系统设计
方程←→框图用变换域方法和梅森公式简单,后面讨论。
由微分方程画框图例1
例1:已知y”(t) + ay’(t)+ by(t) = f(t),画框图。
解:将方程写为 y”(t) = f(t) –ay’(t) –by(t)
由微分方程画框图例2
例 请画出如下微分方程所代表的系统的系统框图。
解
解法一:
解法二(常用方法):该方程含f(t)的导数,可引入辅助函数画出框图。设辅助函数x(t)满足 x”(t) + 3x’(t)+ 2x(t) = f(t) ,可推导出 y(t) = x’(t) + x(t),它满足原方程。
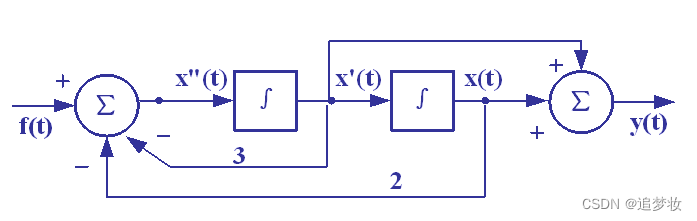
**例3由框图写微分方程
例 **已知框图,写出系统的微分方程。
解 设辅助变量x(t)如图,
例4由框图写差分方程
例 已知框图,写出系统的差分方程。
解 设辅助变量x(k)如图
x(k)= f(k) – 2x(k-1) – 3x(k-2) 即 x(k) +2x(k-1) +3x(k-2) = f(k)
y(k) = 4x(k-1) + 5x(k-2)
消去x(k) ,得 y(k) +2y(k-1) +3y(k-2) = 4f(k-1) + 5f(k-2)
如果已知描述系统的框图,列写其微分方程或差分方程的一般步骤是:
选中间变量x(·)。对于联系系统,设其最右端积分器的输出为x(t);对于离散系统,设其最左端延迟单元的输入为x(k)。
写出各加法器输出信号的方程。
**消去中间变量x(·)**。
1.6 系统的特性和分析方法
1.6.1 系统的定义
系统:具有特定功能的总体,可以看作信号的变换器、处理器。
电系统是电子元器件的集合体。
电路侧重于局部,系统侧重于整体。
电路、系统两词通用。
1.6.2 系统的分类及性质
可以从多种角度来观察、分析研究系统的特征,提出对系统进行分类的方法。常用的分类有:
1.6.2.1 连续系统与离散系统
连续(时间)系统:系统的激励和响应均为连续信号。
离散(时间)系统:系统的激励和响应均为离散信号。
混合系统:系统的激励和响应一个是连续信号,一个为离散信号。如A/D,D/A变换器。
1.6.2.2 动态系统与即时系统
动态系统
动态系统也称为记忆系统。
若系统在任一时刻的响应不仅与该时刻的激励有关,而且与它过去的历史状况有关,则称为动态系统或记忆系统。
含有记忆元件(电容、电感等)的系统是动态系统。
即时系统
如果系统在任意时刻的响应(输出信号)仅取决于该时刻的激励(输入信号),而与它过去的状态无关,就称其为即时系统(或无记忆系统)
全部由无记忆元件(例如电阻)组成的系统是即时系统
即时系统可用代数方程描述
1.6.2.3 单输入单输出系统与多输入多输出系统
单输入单输出系统:系统的输入、输出信号都只有一个。
多输入多输出系统:系统的输入、输出信号有多个。
1.6.2.4 线性系统与非线性系统
线性系统:指满足线性性质的系统。
线性性质:齐次性和可加性
一个既具有分解特性,又具有零状态线性和零输入线性的系统称为线性系统,否则称为非线性系统。
判别方法:①各阶导数是一次方;②没有相乘项;③没有常数项
动态系统是线性系统的条件
动态系统不仅与激励{ f (·) }有关,而且与系统的初始状态{x(0)}有关。 初始状态也称“内部激励”。
y (·) = T [{ f (·) }, {x(0)}], yzs(·) = T [{ f (·) }, {0}], yzi(·) = T [ {0},{x(0)}]
①可分解性: y (·) =yzs(·) + yzi(·)
②零状态线性: T[{af1(t) +bf2(t) }, {0}] = aT[{ f1 (·) }, {0}] +bT[{ f2 (·) }, {0}]
③零输入线性: T[{0},{ax1(0) +bx2(0)} ]= aT[{0},{x1(0)}] +bT[{0},{x2(0)}]
判断线性系统举例
例 判断下列系统是否为线性系统?
(1) y (t) = 3 x(0) + 2 f (t) + x(0) f (t) + 1
(2) y (t) = 2 x(0) + | f (t)|
(3) y (t) = x^2 (0) + 2 f (t)
解(1) yzs(t) = 2 f (t) +1, yzi(t) = 3 x(0) + 1
显然, y (t) ≠ yzs(t) + yzi(t) 不满足可分解性,故为非线性
(2) yzs(t) = | f (t)|, yzi(t) = 2 x(0)
y (t) = yzs(t) + yzi(t) 满足可分解性;
由于 T[{a f (t) }, {0}] = | af (t)| ≠ a yzs(t) 不满足零状态线性。故为非线性系统。
(3) yzi(t) = x^2 (0),T[ {0},{a x(0) }] =[a x(0)]^2 ≠a yzi(t)不满足零输入线性。故为非线性系统。
判断线性系统举例
例 判断下列系统
是否为线性系统?
解
y (t) = yzs(t) + yzi(t) , 满足可分解性;
T[{a f1(t)+ b f2(t) }, {0}]= aT[{f1(t)}, {0}] +bT[{ f2(t) }, {0}],满足零状态线性;
T[{0},{ax1(0) + bx2(0)} ]= e^(-t) [ax1(0) +bx2(0)] = ae^(-t)x1(0)+ be^(-t)x2(0) = aT[{0},{x1(0)}] +bT[{0},{x2(0)}], 满足零输入线性;
所以,该系统为线性系统。
**微分方程描述系统的线性判断
例 **判断下述微分方程所对应的系统是否为线性系统?
分析根据线性系统的定义,证明此系统是否具有齐次性和可加性。可以证明:
系统不满足均匀性 系统不满足均匀性 所以此系统为非线性系统。
证明齐次性
规范性
1.6.2.5 时不变系统与时变系统
时不变系统:指满足时不变性质的系统。
时不变性(或移位不变性)
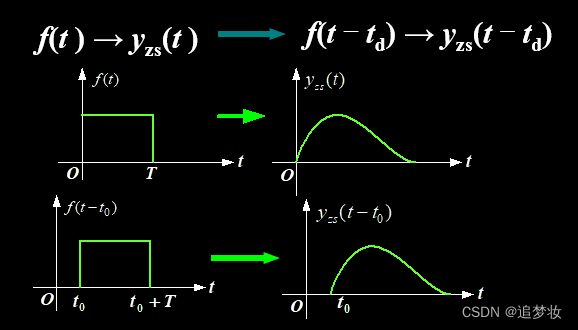
判断时不变系统举例
例 判断下列系统是否为时不变系统?
(1) yzs(k) = f (k) f (k –1)
(2) yzs (t) = t f (t)
(3) y zs(t) = f (– t)
解(1) 令g (k) = f(k –kd)
T[{0}, g (k)] = g(k) g (k –1) = f (k –kd) f (k–kd –1 )
而 yzs (k –kd) = f (k –kd) f (k–kd –1)
显然 T[{0},f(k –kd)] = yzs (k –kd) 故该系统是时不变的。
(2) 令g (t) = f(t –td) , T[{0}, g (t)] = t g (t) = t f (t –td)
而 yzs (t –td)= (t –td) f (t –td)
显然T[{0},f(t –td)] ≠ yzs (t –td) 故该系统为时变系统。
(3) 令g (t) = f(t –td) ,
T[{0},g (t) ] = g (– t) = f(– t –td)
而 yzs (t –td) = f [–( t – td)],显然
T[{0},f(t –td)] ≠ yzs (t –td)
故该系统为时变系统。
LTI连续系统的微分特性和积分特性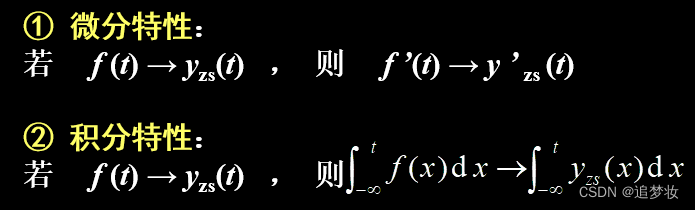
LTI系统微分特性证明
直观判断方法:若f (·)前出现变系数,或有反转、展缩变换,则系统为时变系统。
1.2.6.6 因果系统与非因果系统
因果系统:指零状态响应不会出现在激励之前的系统。即对因果系统, 当t < t0 ,f(t) = 0时,有t < t0 ,yzs(t) = 0。
对于任意时刻满足,不以0为分界。
判断方法:输出不超前于输入。
因果系统判断举例
如下列系统均为因果系统:而下列系统为非因果系统:
(1) yzs(t) = 2f(t + 1),因为,令t=1时,有yzs(1) = 2f(2)
(2) yzs(t) = f(2t),因为,若f(t) = 0, t < t0 ,有yzs(t) = f(2t)=0, t < 0.5 t0 。
实际的物理可实现系统均为因果系统
非因果系统的概念与特性也有实际的意义,如信号的压缩、扩展,语音信号处理等。
若信号的自变量不是时间,如位移、距离、亮度等为变量的物理系统中研究因果性显得不很重要。
因果信号
t = 0接入系统的信号称为因果信号。可表示为:
1.6.2.7 稳定系统与不稳定系统
一个系统,若对有界的激励f(.)所产生的零状态响应yzs(.)也是有界时,则称该系统为有界输入有界输出稳定,简称稳定。即 若│f(.)│<∞,其│yzs(.)│<∞ 则称系统是稳定的。
判断例题

1.2.7 综合举例
例 某LTI因果连续系统,起始状态为x(0–)。
已知,当x(0–) =1,输入因果信号f1(t)时,全响应 y1(t) = e ^(–t) + cos(πt),t>0;
当x(0-) =2,输入信号f2(t)=3f1(t)时,全响应 y2(t) = –2e^(–t) +3 cos(πt),t>0;
求输入f3(t) =f1'(t)+2f1(t-1)时,系统的零状态响应y3f(t) 。解 设当x(0–) =1,输入因果信号f1(t)时,系统的零输入响应和零状态响应分别为y1zi(t)、y1zs(t)。当x(0-) =2,输入信号f2(t)=3f1(t)时,系统的零输入响应和零状态响应分别为y2zi(t)、y2zs(t)。
由题中条件,有
y1(t) =y1zi(t) + y1zs(t) = e^(–t) + cos(πt),t>0 (1)
y2(t) = y2zi(t) + y2zs(t) = –2e^(–t) +3 cos(πt),t>0 (2)
根据线性系统的齐次性,y2zi(t) = 2y1zi(t),
y2zs(t) =3y1zs(t),代入式(2)得
y2(t) = 2y1zi(t) +3 y1zs(t) = –2e^(–t) +3 cos(πt),t>0 (3)
式(3)– 2×式(1),得
y1zs(t) = –4e^(-t) + cos(πt),t>0
由于y1zs(t) 是因果系统对因果输入信号f1(t)的零状态响应,故当t<0,y1zs(t)=0;因此y1zs(t)可改写成
y1zs(t) = [–4e^(-t) + cos(πt)]ε(t) (4)
——————分割线
这次很多内容都是数字转过来的,现在觉得或许图片更加形象地对此进行描述,以后注意。
同时,我也正在进行了微总结~~~
版权归原作者 追梦妆 所有, 如有侵权,请联系我们删除。