高擎机电12自由度双足机器人pai的算法开源|传统控制篇

介绍

为了方便开发者使用我们的平台，本次开源的算法在12自由度的pai上面进行了仿真验证。

本次开源的算法是基于桥介数物（BridgeDP）的hunter_bipedal_control做的一些改进，包括对踝关节两自由度的锁定，使其同步成为一个自由度，以及适配高擎自己开发的SDK接口，用于真机调试。

开源的代码放在了github上，项目名为livelybot_dynamic_control：

https://github.com/HighTorque-Robotics/livelybot_dynamic_control.git

README.md有详细的配置过程。

仿真环境

本框架使用gazebo进行仿真，同时支持rivz查看机器人的状态以及规划轨迹，gazebo的环境安装可以直接使用鱼香ROS的一键安装，安装ubuntu20.04对应的noetic版本的ros环境，该环境包含gazebo。搭建仿真环境的过程为，使用solidworks的urdf插件将图纸导出为urdf。

一个注意事项，solidworks的urdf插件直接导出的转动惯量矩阵是错误的，你需要自行修改urdf中的转动惯量矩阵。具体的做法是，使用solidworks的“评估-质量属性”功能，在选项中设置单位制，设置当前link所对应坐标系的坐标值，设置为负张量计数法（要求solidworks版本至少为2021SP5），并使用“由重心决定，并且对齐输出的坐标系。（使用负张量记数法。）”的惯性矩阵。

导出的urdf不能直接给gazebo使用，需要添加gazebo_ros_control插件，以及一些传感器和执行器插件等，具体如下：

<gazebo> //以及gazebo_ros_control插件
    <plugin name="gazebo_ros_control" filename="libhunter_bipedal_hw_sim.so">
      <robotNamespace>/</robotNamespace>
      <robotParam>legged_robot_description</robotParam>
      <robotSimType>legged_gazebo/LeggedHWSim</robotSimType>
    </plugin>
</gazebo>

<gazebo>  //imu插件
    <plugin filename="libgazebo_ros_p3d.so" name="p3d_base_controller">
      <alwaysOn>true</alwaysOn>
      <updateRate>500.0</updateRate>
      <bodyName>base_link</bodyName>
      <topicName>ground_truth/state</topicName>
      <gaussianNoise>0</gaussianNoise>
      <frameName>world</frameName>
      <xyzOffsets>0 0 0</xyzOffsets>
      <rpyOffsets>0 0 0</rpyOffsets>
    </plugin>
  </gazebo>

  <transmission name="leg_r1_tran">   //执行器标签
    <type>transmission_interface/SimpleTransmission</type>
    <joint name="leg_r1_joint">
      <hardwareInterface>hardware_interface/EffortJointInterface</hardwareInterface>
    </joint>
    <actuator name="leg_r1_motor">
      <hardwareInterface>hardware_interface/EffortJointInterface</hardwareInterface>
      <mechanicalReduction>1</mechanicalReduction>
            <maxVelocity>1.484</maxVelocity><!-- 85rpm -->
      <maxEffort>36.0</maxEffort><!-- 36Nm -->
    </actuator>
  </transmission>

添加这些信息以后才可以被gazebo使用。gazebo下pai位置控制的效果如下图：

控制算法框架介绍

这套开源算法的框架是分为ocs2提供的非线性模型预测控制（NMPC）和廖洽源legged_control实现的全身控制（Whole body control）。

NMPC

OCS2全名是Optimal Control for Switched Systems，是一个专门为机器人MPC控制设计的最优控制的仓库，包括使用pinocchio动力学库自动构建机器人的全身动力学模型，从urdf自动构建优化问题，并快速实现最优控制算法。OCS2提供了OCS2 dummy功能包，该功能包可以单独对OCS2的计算结果进行调试。遗憾的是，它的官方文档非常少，大部分都是介绍性的文档。如果需要了解其详细使用方法，需要配合着Robotic Systems Lab: Legged Robotics at ETH Zürich的相关论文，论文库链接rsl.ethz.ch，以及阅读其例程中的源代码。本算法主要参考了其四足机器人的demo，参见OCS2_legged_robot和OCS2_legged_robot_ros。运行方法参考官方文档。

足端轨迹规划

在原本的OCS2中，足端轨迹只规划了Z轴方向的，没有规划X，Y轴方向的轨迹，在本开源算法中添加了X,Y轴方向的轨迹，摆动曲线为三次样条曲线。

在每个周期中，NMPC部分通过OCS2提供的接口来解决以下优化问题：

其中 $\mathbf{h}_{com} \in \mathbb{R}^6$ 是归一化的质心动量， $\mathbf{q}=[\mathbf{q}_b^T, \mathbf{q}_j^T]^T$ 是广义坐标的位置，其中 $\mathbf{q}_b^T$ 是浮动基的6自由度位置， $\mathbf{q}_j^T$ 是每个实体关节的位置，由于我们对urdf中的脚踝关节进行了操作，有效实体关节的数量是10个，机器人的状态 $\mathbf{x} = [\mathbf{\theta}^T,\mathbf{p}^T,\mathbf{\omega}^T,\mathbf{v}^T,\mathbf{q}_j^T]$ 一共是22个维度,前12为是浮动基的姿态位置和其对应的微分，后10维是关节的位置。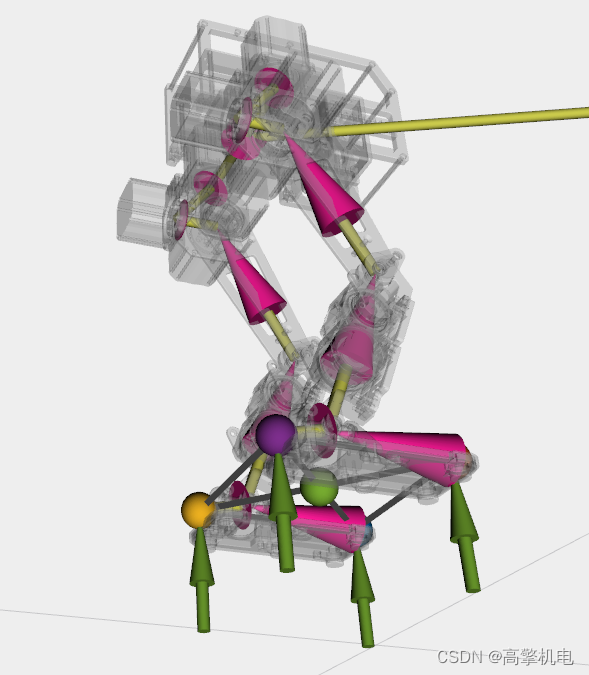控制输入的形式 $\mathbf{u} = [\mathbf{f}^T,\mathbf{\dot{q}}_j^T]$ ，也是22维，其中 $\mathbf{f} \in \mathbb{R}^{12}$ 是包含四个接触点的接触力。在这个框架中我们定义了四个3自由度的接触点，分别对应左右脚的脚尖和脚后跟，如下图所示：

优化问题成本函数是追踪所有状态和输入误差的二次误差，系统动力学模型使用质心动力学模型，并包含以下约束：

摩擦锥约束；
站立脚无运动；
摆动脚不受地面反力；
摆动脚的z轴位置满足步态生成的曲线；
脚的滚转轴（roll）无运动。

为了解决这个最优控制问题，采用多重打靶法（Multi-Shooting）将最优控制问题转化为非线性规划（NLP）问题，并使用序列二次规划（SQP）来解决NLP问题。QP子问题使用最强非线性优化库HPIPM来解决。

值得注意的是，受益于OCS2强大的From URDF to OCP的功能，你不需要自己实现优化代价、质心动力学方程（即system flow map）的公式，只需要调用相应的接口自动生成即可。不过，其它的约束函数需要你自己来实现。OCS2需要你定义约束函数的值以及对状态和输入的导数值，从而实现约束函数的线性化。对于足端约束，OCS2实现了EndEffectorKinematics类从而计算足端的运动学和运动学导数。相关代码参见legged_interface文件夹。

Weighted WBC

WBC仅考虑当前时刻的状态，不能用于预测控制，其接受来自MPC优化出的足底反力，作为WBC的优化约束，同时也从状态估计器中获取姿态信息，以及质心轨迹和足端轨迹当前时刻规划出的位置和速度。WBC最终也可以描述成一个二次规划（QP）问题。根据qpOASES，WBC优化的形式可以写成:

其中 $\mathbf{x}$ 是优化变量，在该模型下的维度是46，定义如下：

$\mathbf{x} = [\mathbf{\ddot{q}}^T, \mathbf{f}_c^T, \mathbf{\tau}^T]^T$

其中 $\mathbf{\ddot{q}}$ 是关节空间加速度，包含浮动基， $\mathbf{f}_c$ 是WBC优化出的接触力, $\mathbf{\tau}$ 是实体关节力矩。

WBC的构建过程：

$\mathbf{M}\mathbf{\ddot{q}} + \mathbf{C} + \mathbf{g} = \mathbf{J}_c^T\mathbf{f}_c + \mathbf{S}_j\mathbf{\tau}$

$\mathbf{\ddot{T}}_{task} = \mathbf{\dot{J}}\mathbf{\dot{q}} + \mathbf{J}\mathbf{\ddot{q}}$

整理上式有：

$\begin{bmatrix} \mathbf{M} & \mathbf{J}_c^T & \mathbf{S}_{\tau} \\ \mathbf{J} & \mathbf{0} & \mathbf{0} \ \end{bmatrix} \begin{bmatrix} \mathbf{\ddot{q}}\\ \mathbf{f}_c \\ \mathbf{\tau}\end{bmatrix} = \begin{bmatrix} -\mathbf{C}-\mathbf{g}\\ \mathbf{\ddot{T}_{task} -\mathbf{\dot{J}}\mathbf{\dot{q}} } \end{bmatrix}$

可以将上式看作是 $\mathbf{AX = B}$

cost function:

$mini cost = 1/2(\mathbf{AX-B})^T\mathbf{Q}(\mathbf{AX-B}) + \mathbf{X}^T\mathbf{R}\mathbf{X}$

约束包括摩擦锥约束和关节力矩约束，以及MPC求解出的力约束。

控制器集成

控制根据用户命令，计算MPC状态变量的参考轨迹，从仿真环境（或机器人硬件）中获取传感器的值，调用状态观测器，计算出MPC中的状态变量的观测值，调用MPC控制算法，计算出状态和输入的目标轨迹，将目标轨迹传输给WBC进行优化，得到目标关节力矩和目标关节加速度。再从MPC中获取关节位置和关节速度的当前目标（从目标轨迹获取），传入ros_control的setCommand接口，然后将控制指令发送给电机。关节的位置和速度可以有WBC优化出的加速度积分得到，具体参见LeggedController.cpp这个文件。

标签：机器人

本文转载自: https://blog.csdn.net/hightorque/article/details/138350833
版权归原作者 高擎机电 所有，如有侵权，请联系我们删除。

高擎机电12自由度双足机器人pai的算法开源|传统控制篇

发表评论

“高擎机电12自由度双足机器人pai的算法开源|传统控制篇”的评论:

关于作者

overfit同步小助手

相关阅读

文章导航