基于方差阈值的特征选择介绍
今天,数据集拥有成百上千个特征是很常见的。从表面上看,这似乎是件好事——每个样本的特征越多,信息就越多。但通常情况下,有些特征并没有提供太多价值,而且引入了不必要的复杂性。
机器学习最大的挑战是通过使用尽可能少的特征来创建具有强大预测能力的模型。但是考虑到今天庞大的数据集,很容易忽略哪些特征是重要的,哪些是不重要的。
这就是为什么在ML领域中有一个完整的技能需要学习——特征选择。特征选择是在尽可能多地保留信息的同时,选择最重要特征子集的过程。
举个例子,假设我们有一个身体测量数据集,如体重、身高、BMI等。基本的特征选择技术应该能够通过发现BMI可以用体重和身高来进行表示。
在本文中,我们将探索一种称为方差阈值的特征选择( Variance Thresholding)技术。这种技术是一种快速和轻量级的方法来消除具有非常低方差的特征,即没有太多有用信息的特征。
关于方差的说明
方差:顾名思义,在一个单一的度量中显示分布的可变性。它显示了分布是如何分散的,并显示了平均距离的平方:
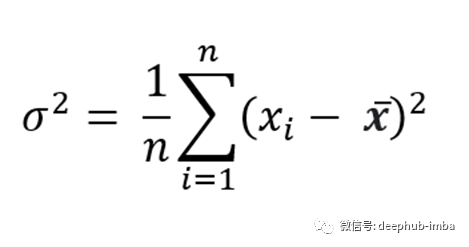
显然,具有较大值的分布会产生较大的方差,因为每个差异都进行了平方。但是我们在ML中关心的主要事情是分布实际上包含有用的信息。例如,考虑以下分布:
dist_1 = [2, 2, 2, 2, 2, 2, 2, 2]
>>> np.std(dist_1)
0.0
用Numpy计算方差表明,该分布的方差为0,换句话说,这个数据完全没有意义。使用零方差的特性只会增加模型的复杂性,而不会增加它的预测能力。考虑另一个:
dist_2 = [5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 6]
>>> np.std(dist_2)
0.28747978728803447
类似的,这个几乎是由一个常数组成的。围绕单个常量而存在少数例外的分布也是无用的。换句话说,任何方差接近0的特性或分布都应该删除。
如何使用Scikit-learn的方差阈值估计
手动计算方差和阈值可能需要很多工作。但是Scikit-learn提供了方差阈值估计器,它可以为我们做所有的工作。只要设置一个临界值,所有低于该临界值的特征都将被删除。
为了演示VarianceThreshold,我们将使用Ansur数据集(https://www.kaggle.com/seshadrikolluri/ansur-ii)。这个数据集以各种可以想象的方式记录人体的测量数据。男性和女性数据集包含近6000(4000名男性,2000名女性)美国陆军人员的108个特征或测量。我们将重点关注男性数据集:
ansur_male = pd.read_csv('data/ansur_male.csv',
encoding='latin').drop('subjectid', axis=1)
>>> ansur_male.head()

首先,我们去掉方差为零的特征。我们将从sklearn.feature_selection中导入VarianceThreshold:
from sklearn.feature_selection import VarianceThreshold
vt = VarianceThreshold()
我们像任何其他Scikit-learn估计器一样初始化它。阈值的默认值总是0。而且,估计器显然只对数字数据有效,如果数据中存在分类特征,估计器就会抛出错误。所以我们需要把数字特性子集放到另一个dataframe中:
ansur_male_num = ansur_male.select_dtypes(include='number')
>>> ansur_male_num.shape
(4082, 98)
我们有98个数字特征。现在让我们将估计量与数据进行拟合,得到结果:
transformed = vt.fit_transform(ansur_male_num)
>>> transformed
array([[ 266, 1467, 337, ..., 41, 71, 180],
[ 233, 1395, 326, ..., 35, 68, 160],
[ 287, 1430, 341, ..., 42, 68, 205],
...,
[ 264, 1394, 313, ..., 23, 67, 186],
[ 203, 1417, 327, ..., 22, 69, 165],
[ 327, 1523, 358, ..., 38, 73, 218]], dtype=int64)
直接调用fit_transform将以numpy数组的形式返回dataframe,并删除特性。但有时,我们不希望得到那种格式的结果,因为列名将被删除。考虑选择:
_ = vt.fit(ansur_male_num)
mask = vt.get_support()
首先,我们将估计器与数据相匹配,并调用它的get_support()方法。对于未删除的列,它返回一个为真值的布尔类型的掩码。然后我们可以使用这个掩码来像这样划分数据:
ansur_male_num = ansur_male_num.loc[:, mask]
让我们看下dataframe的形状,看看是否有任何常量列:
>>> ansur_male_num.shape
(4082, 98)
我们仍然有相同数量的特征,让我们删除方差接近0的特征:
vt = VarianceThreshold(threshold=1)
# Fit
_ = vt.fit(ansur_male_num)
# Get the boolean mask
mask = vt.get_support()
ansur_reduced = ansur_male_num.loc[:, mask]
>>> ansur_reduced.shape
(4082, 97)
阈值为1时,只有1个特征被删除了。
比较方差与特征归一化
通常,比较一个特性与另一个特性的差异是不公平的。原因是随着分布中的值变大,方差呈指数增长。换句话说,差异将不会在相同的尺度上。考虑一下这个例子:
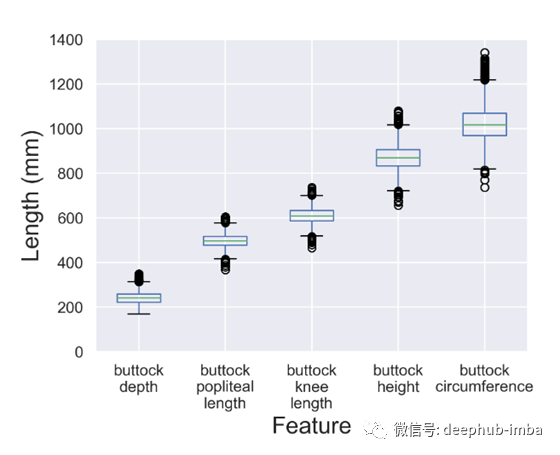
以上特征均具有不同的中位数,四分位数和范围完全不同的分布。我们无法将这些功能相互比较。
我们可以使用的一种方法是通过将所有特征除以均值来对其进行归一化:
normalized_df = ansur_male_num / ansur_male_num.mean()
>>> normalized_df.head()

此方法可确保所有方差都在同一范围内:
>>> normalized_df.var()
abdominalextensiondepthsitting 0.021486
acromialheight 0.001930
acromionradialelength 0.002720
anklecircumference 0.004080
axillaheight 0.002005
...
SubjectNumericRace 85.577697
DODRace 0.390651
Age 0.085336
Heightin 0.001771
Weightlbs 0.025364
Length: 98, dtype: float64
现在,我们可以使用阈值下限较低的估算器,例如0.005或0.003:
vt = VarianceThreshold(threshold=.003)
# Fit
_ = vt.fit(normalized_df)
# Get the mask
mask = vt.get_support()
# Subset the DataFrame
ansur_final = ansur_male_num.loc[:, mask]
>>> ansur_final.shape
(4082, 48)
如您所见,我们从数据集中删除50个特征。下一步就是测试一下是删除的这些特征对训练模型产生的影响。
我们将通过训练两个RandomForestRegressor来预测一个人的体重(以磅为单位)来检查这一点:第一个在最终的特征选择后的数据集中训练,第二个在全部的仅具有数字特征的数据集中。
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
# Build feature, target arrays
X, y = ansur_final.iloc[:, :-1], ansur_final.iloc[:, -1]
# Train/test split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.3, random_state=1121218)
# Init, fit, score
forest = RandomForestRegressor(random_state=1121218)
_ = forest.fit(X_train, y_train)
# Training Score
>>> print(f"Training Score: {forest.score(X_train, y_train)}")
Training Score: 0.988528867222243
>>> print(f"Test Score: {forest.score(X_test, y_test)}")
Test Score: 0.9511616691995844
训练和测试分数都表明,在没有过度拟合的情况下,确实具有很高的性能。现在,让我们在完整的仅数字数据集上训练相同的模型:
# Build feature, target arrays
X, y = ansur_male_num.iloc[:, :-1], ansur_male_num.iloc[:, -1]
# Train/test split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.3, random_state=1121218)
# Init, fit, score
forest = RandomForestRegressor(random_state=1121218)
_ = forest.fit(X_train, y_train)
# Training Score
>>> print(f"Training Score: {forest.score(X_train, y_train)}")
Training Score: 0.9886396641558658
>>> print(f"Test Score: {forest.score(X_test, y_test)}")
Test Score: 0.9495977505935259
即使删除了50个特征,我们仍然能够构建强大的模型。
总结
尽管方差阈值处理是一种简单的方法,但是在执行特征选择时还是非常有用的。但是需要强调下,此技术未考虑要素之间的关系或特征与目标之间的关系。
作者:Bex T.
deephub翻译组