图解人工智能的数学基础（线性代数）

🌞欢迎来到人工智能的世界
🌈博客主页：卿云阁

💌欢迎关注🎉点赞👍收藏⭐️留言📝

🌟本文由卿云阁原创！

📆首发时间：🌹2024年6月9日🌹

✉️希望可以和大家一起完成进阶之路！

🙏作者水平很有限，如果发现错误，请留言轰炸哦！万分感谢！

🙏本书是自己写的哦，因为编辑太麻烦啦，很多地方就粘贴了图片，如果需要电子版的可以私信哈。

---

引言

   向量的定义为具有大小和方向的量。这里我们主要关注神经网络中用到的内容，弄清向量的性质。

研究对象：向量

   向量是有方向的线段，线段的长度代表向量的大小，箭头代表向量的方向。

几何视角和坐标表示

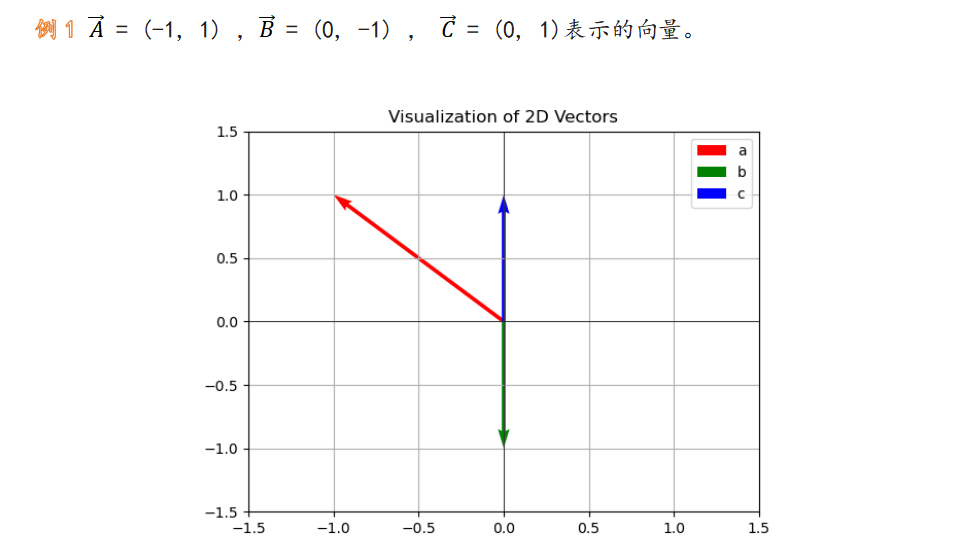
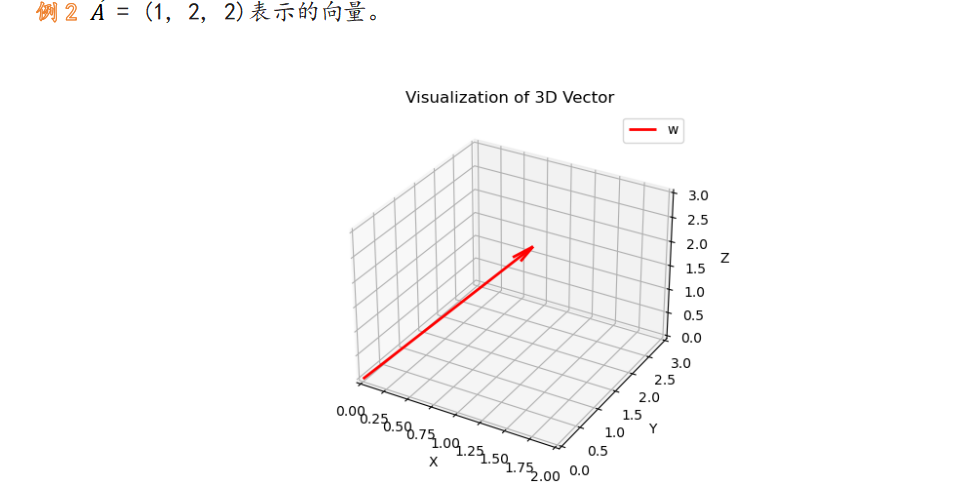
现实视角

向量可以代表着一些信息

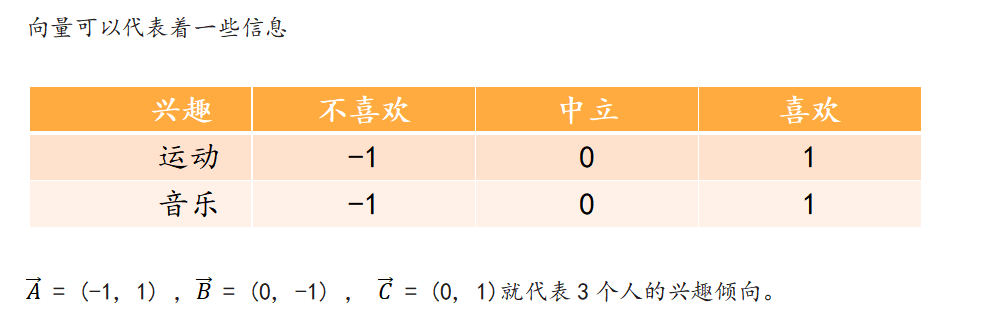
向量的大小

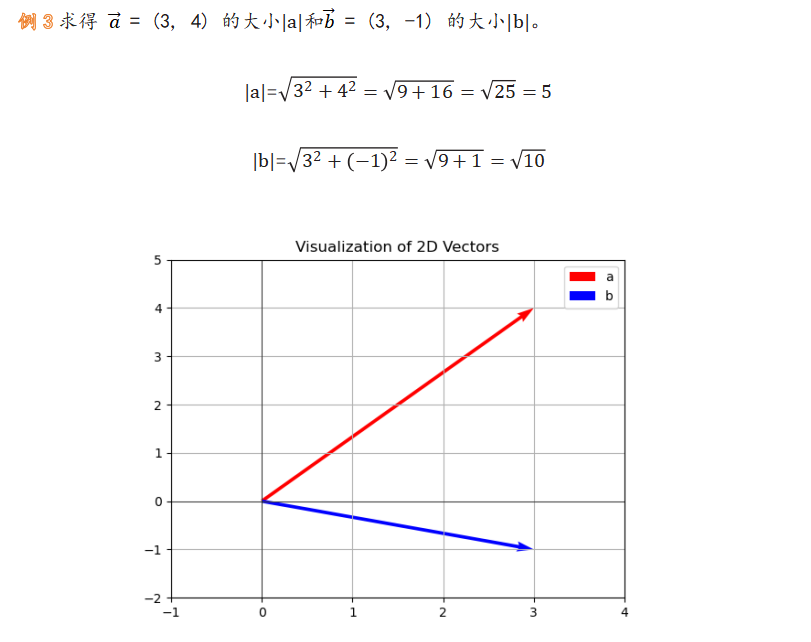
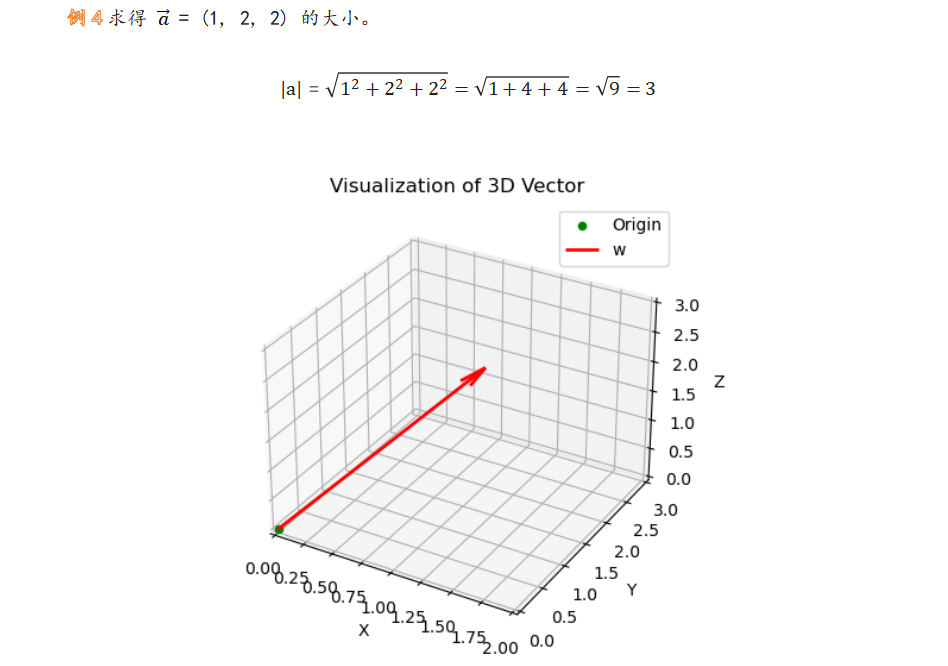
向量的内积

坐标视角

****几何视角 ****

   从几何角度来看，向量内积与向量的长度和它们之间的夹角有关。具体地，两个向量的内积可以表示为：

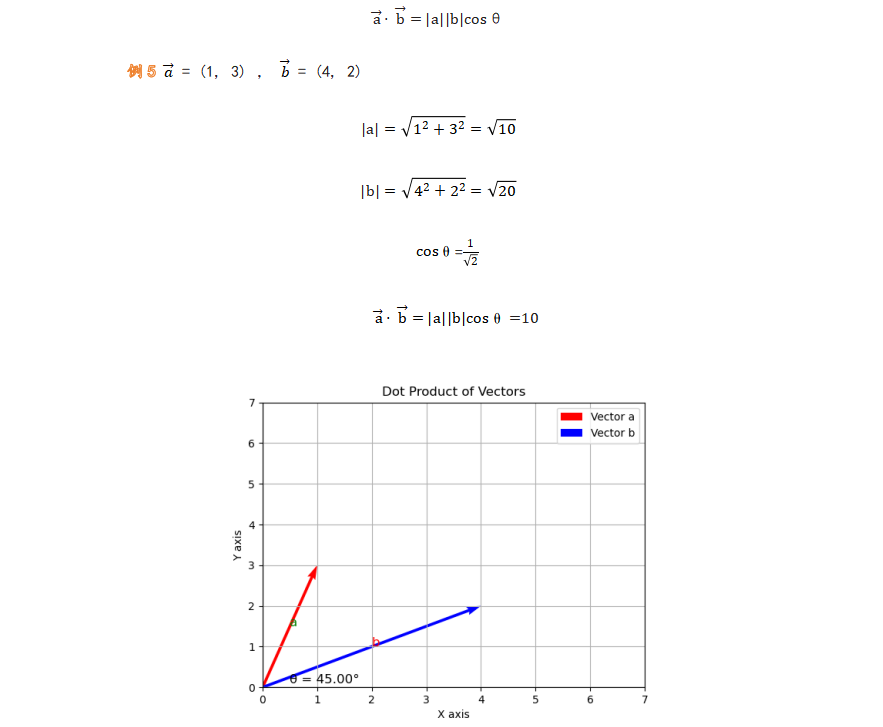
研究手段：线性变换

对称变换

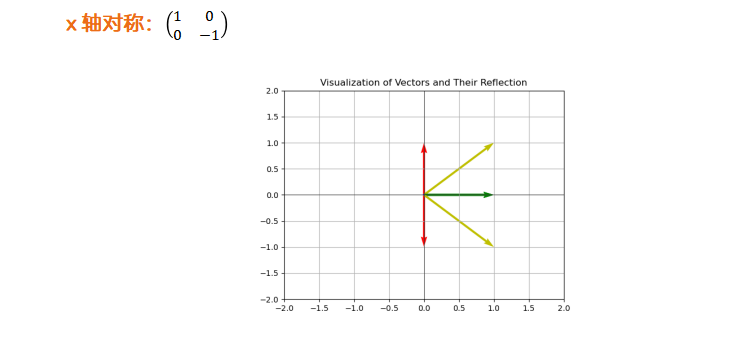
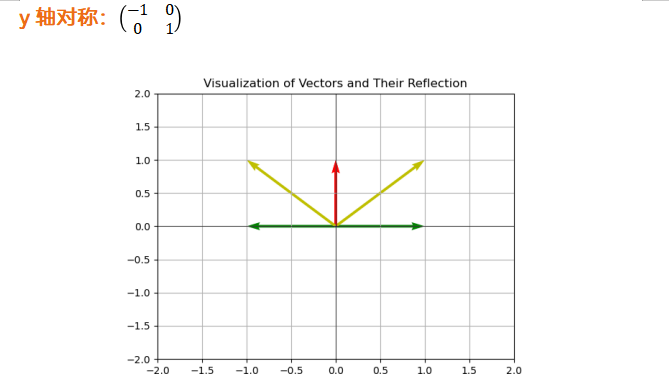
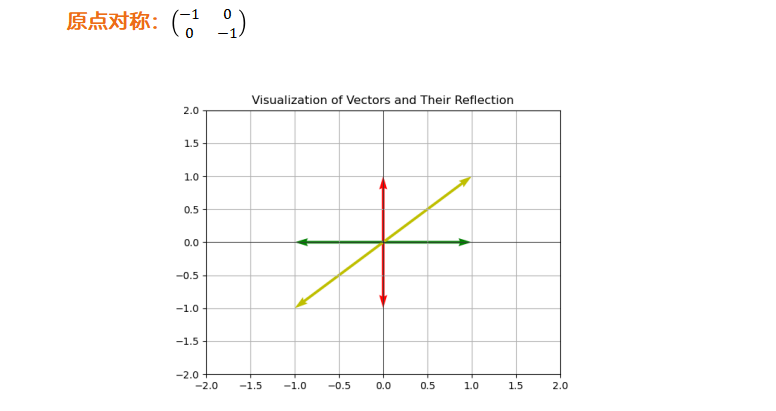
伸缩变换

---

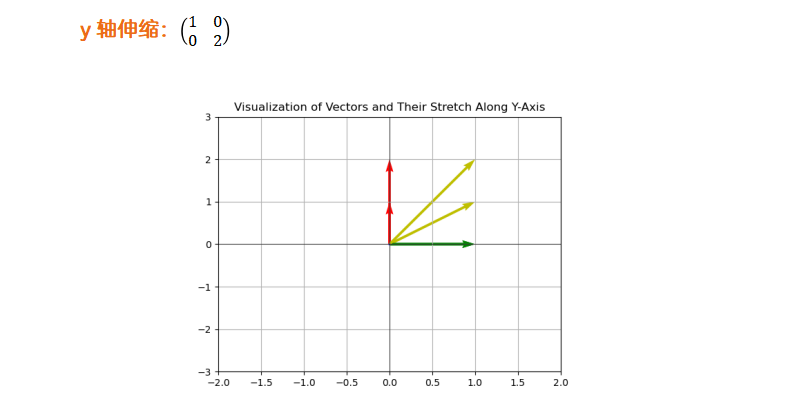
行列式

    矩阵是为了表达信息，行列式可以当成矩阵的一个性质。二维行列式的几何含义就是二维图像的有向面积。三维行列式的几何含义就是三维集合的有向体积。如果这个矩阵参与变换的话，对应的二维行列式的含义就是变换前后的有向面积之比。对应的三维行列式的几何含义就是变换前后的有向体积之比。 

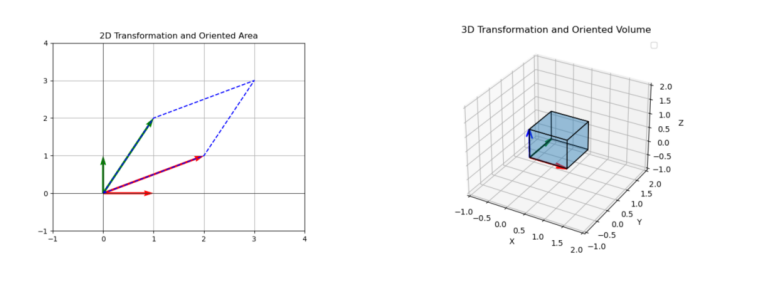
   对于行列式的计算而言，在实际的工程应用中直接可以用计算机计算，这里我们不做重点进行讨论。

---

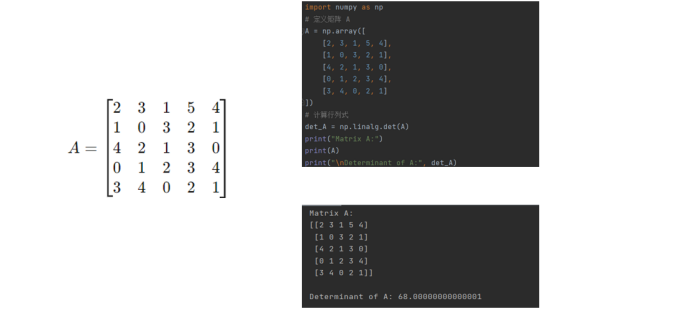
矩阵

矩阵的含义

    一个标量就是一个单独的数。只具有数值大小，没有方向（部分有正负之分），运算遵循一般的代数法则。比如质量是数据标量。向量指具有大小和方向的量，在机器学习中，单条数据样本的表征都是以向量化的形式来完成的。矩阵是二维数组，****AI中的应用：样本以矩阵形态表示： 公式条数据/样本，公式个特征的数据集，就是一个公式 的矩阵。****

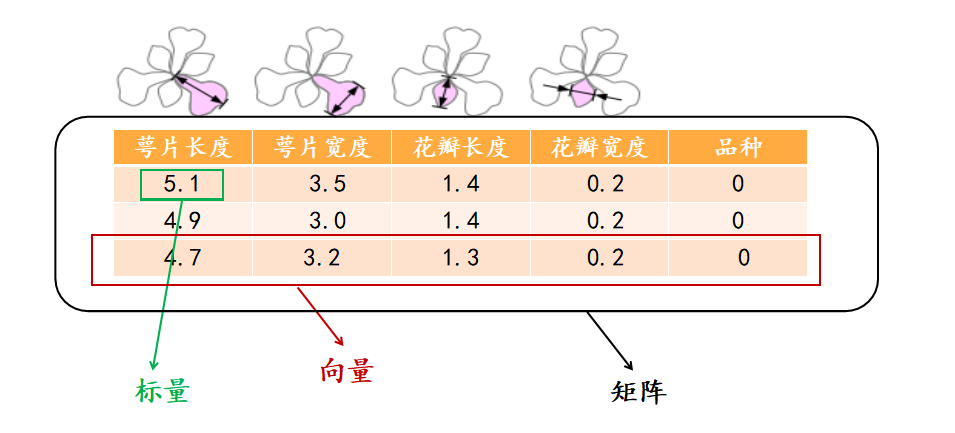
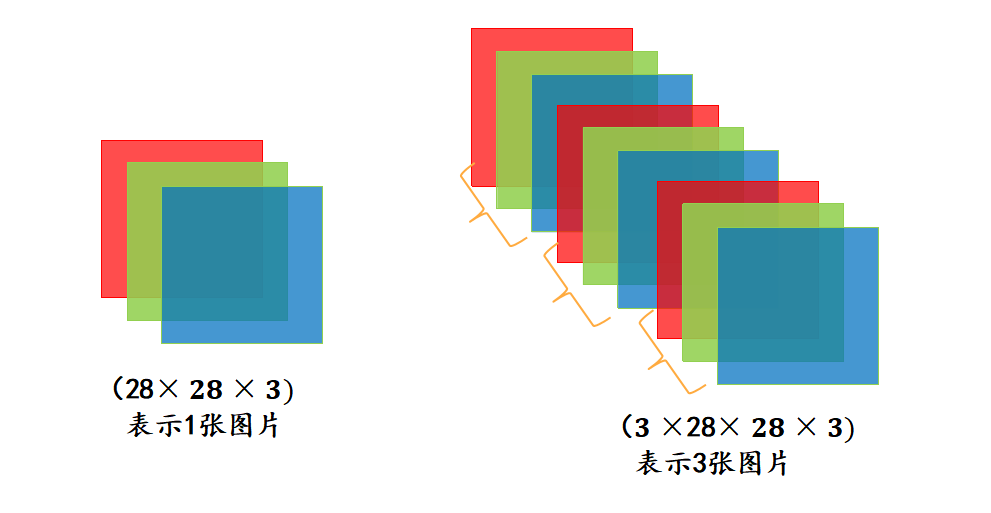
    标量，可以视为零阶张量。向量，可以视为一阶张量。矩阵，可以视为二阶张量。图片以矩阵形态表示：将一张彩色图片表示成一个公式的三阶张量（高度，宽度，通道）。 在这个例子的基础上，将这一定义继续扩展，即：用四阶张量（样本，高度，宽度，通道）表示一个包含多张图片的数据集。AI中的应用：张量是深度学习中一个非常重要的概念，大部分的数据和权重都是以张量的形态存储的，后续的所有运算和优化算法也都是基于张量进行的。

矩阵的运算

   矩阵的运算有很多种，比如加减法，数乘，乘法，转置等等，每种运算都有现实含义和工程应用，这里我们讨论矩阵的乘法和转置的应用。

矩阵的乘法

矩阵的转置

    在现实问题中，系统信息表示的矩阵可能不是一个方阵，为了挖掘出这个数据集更多的信息，会左乘这个矩阵的转置，使其变成一个方阵，这个方阵中会包含更多的信息。

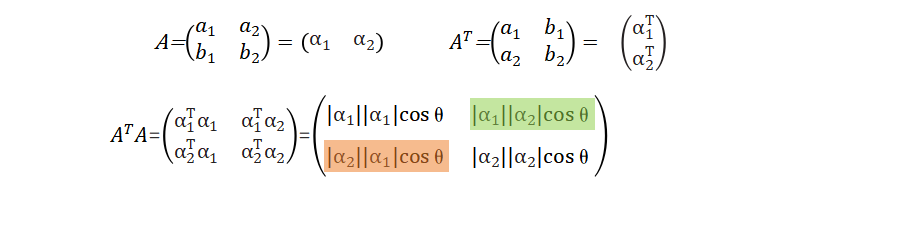
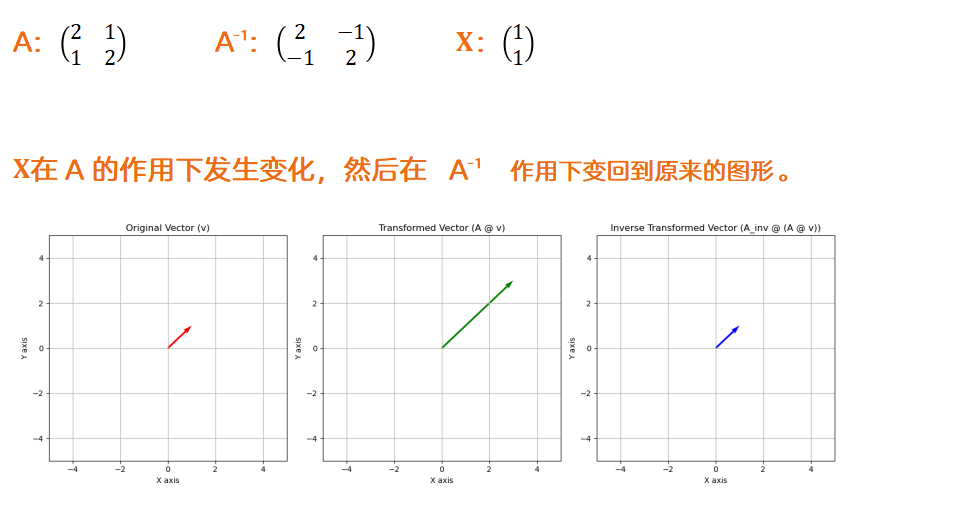
矩阵的逆

逻辑角度

我们知道矩阵没有乘法，但是我们可以乘以一个逆数，这实现了同样的事情。

如何与 2 个人分享 10 个苹果？

集合角度

现实角度

  如果乘坐公共汽车旅行，每位儿童 3 元，每位成人 3.20 元，总计 118.40 元。如果乘坐火车旅行，每位儿童3.50 元，每位成人 3.60  元，总计 135.20 元。

有多少孩子，有多少成年人？

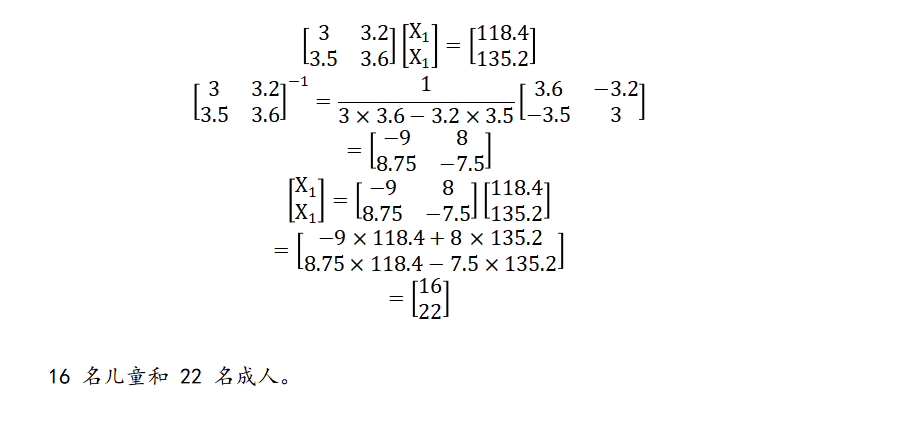
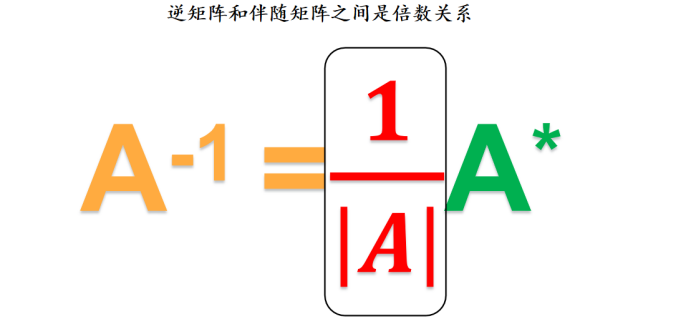
伴随矩阵

    我们发明伴随矩阵的目的就是为了求逆矩阵的，课本上我们学到的是用初等行变换的方式去求逆矩阵，但是初等行变换的方法是不可控的，比较混乱，所以为了计算机可以更加便捷的去求到逆矩阵，所以我们便引入了伴随矩阵。

矩阵相似

定义角度

几何角度

初等行变换对应于在几何上进行基本的几何操作，例如缩放、旋转、平移等。这些操作不会改变变换的本质特性（矩阵和矩阵****的秩相同），只是改变了其表示形式。

矩阵的秩

  矩阵的秩会决定最后的输出y的维度，所以研究矩阵的秩是很有意义的。的秩决定着有效方程的个数。r越小，y的维度越小。

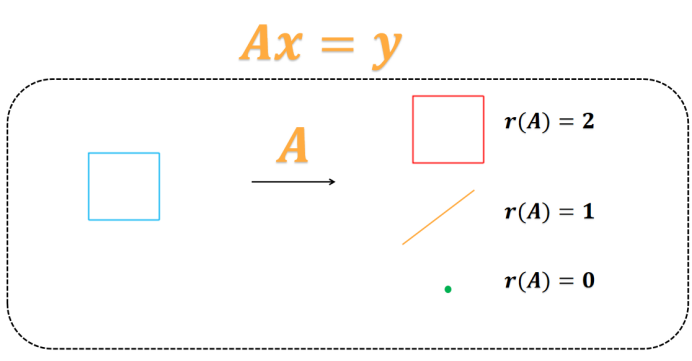
   可以把矩阵看成是一个筛子，矩阵的秩看成是筛眼的大小，矩阵A的秩越小，对应的筛眼越小，自然漏过去的面粉越少。

---

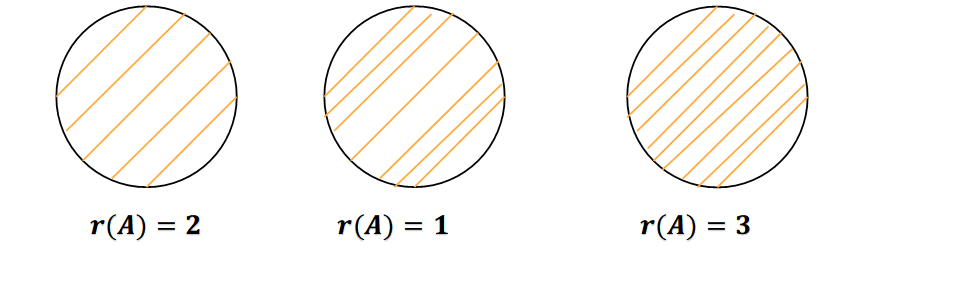
向量

线性组合

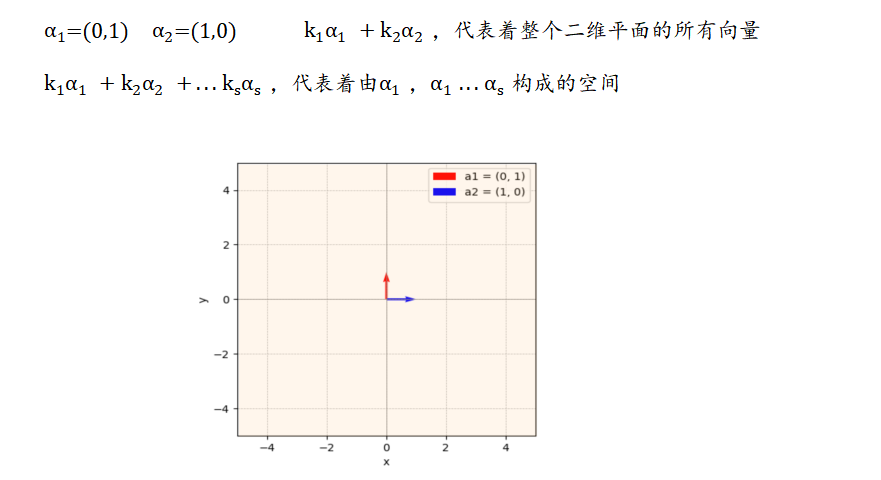
线性表示

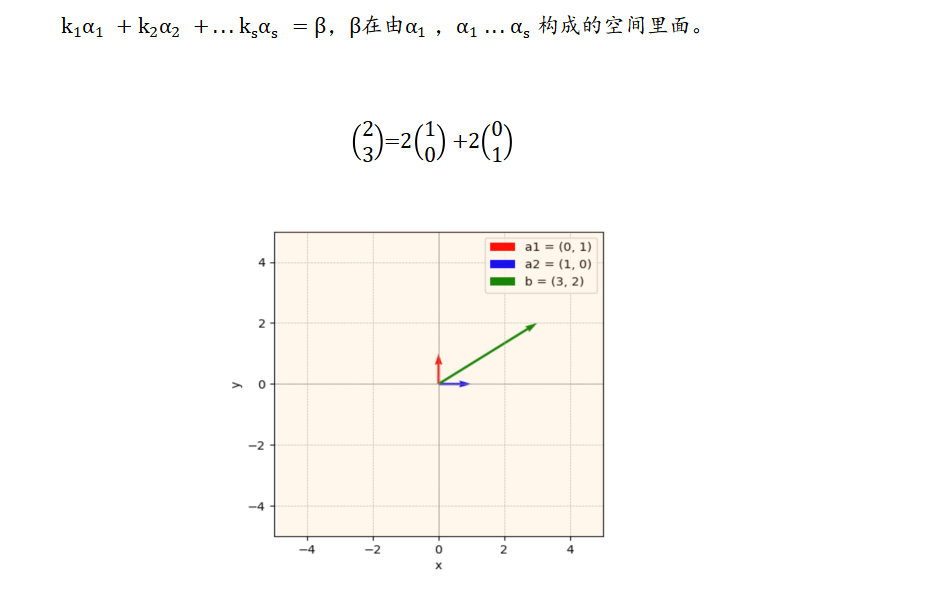
线性相关

线性无关

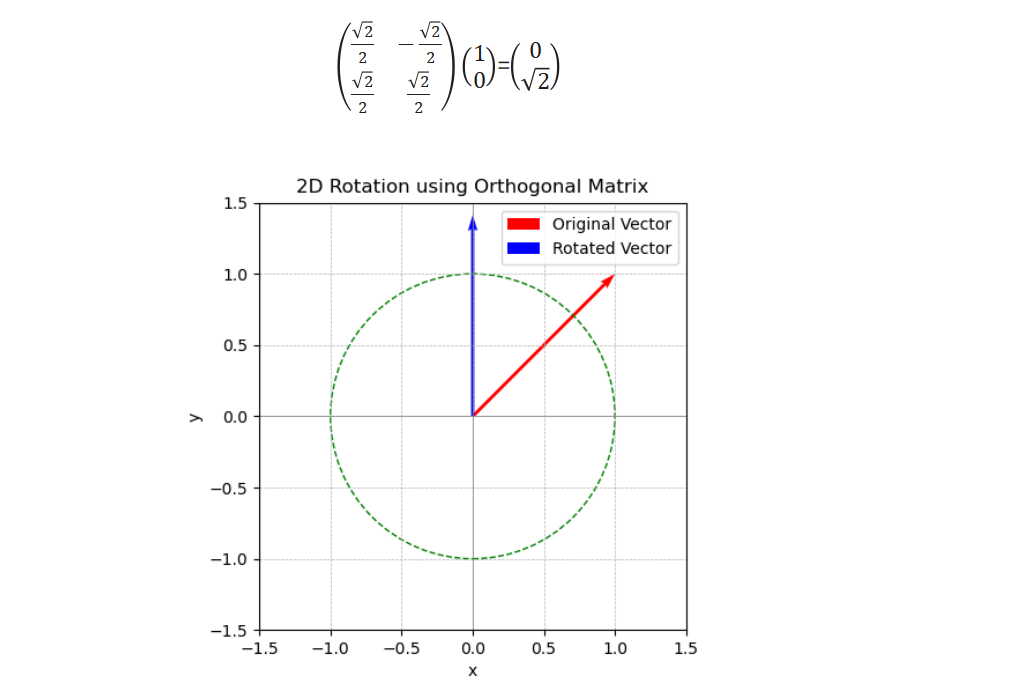
正交矩阵

    它可以改变原始向量的相对位置，保留了向量的长度和角度。（在计算机图形学中，正交矩阵用于表示旋转和反射。这些变换在动画和3D建模中非常重要。例如，3D物体的旋转可以用正交矩阵来表示，从而保持物体的形状和比例不变。）

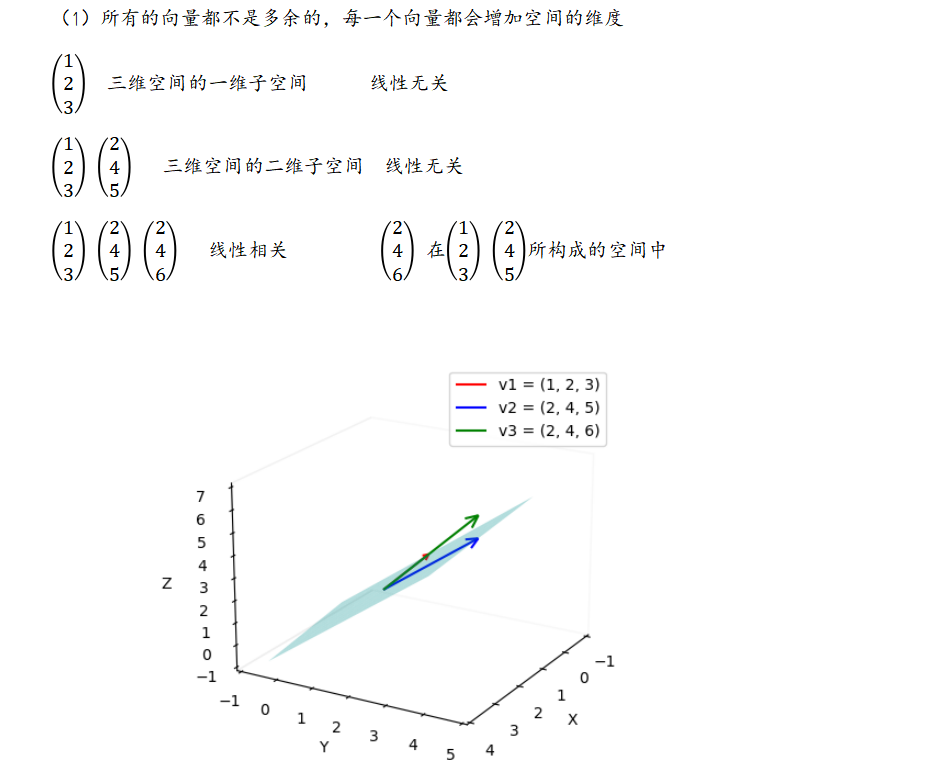
极大线性无关组

所有有效向量（增加空间维度）构成的向量组

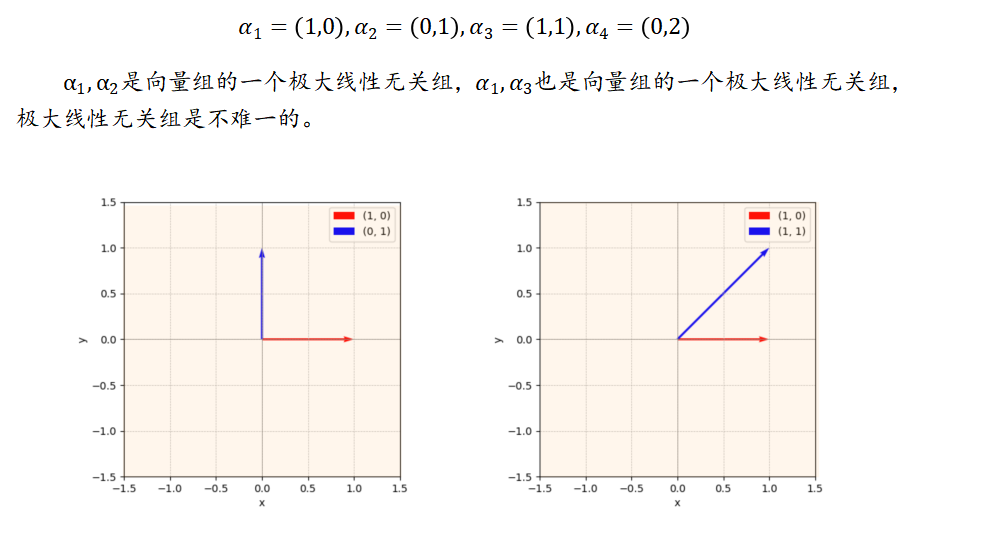
向量组的秩

张成空间的维数，张成的空间是2维的，秩为2。

等价向量组

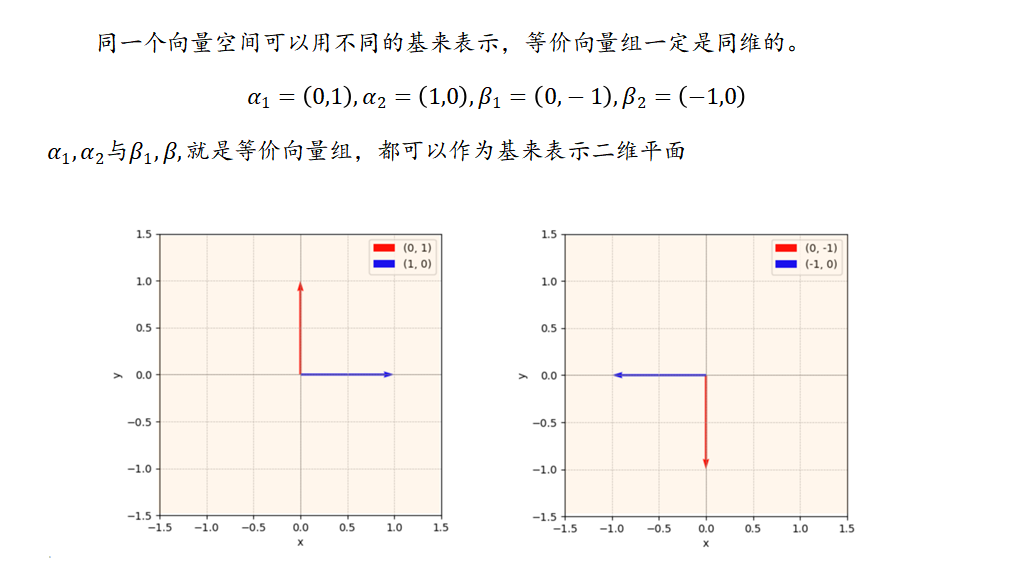
施密特正交化

   非正交基转换为正交基。假设现在有两个向量是二维平面的一组非正交基。我们将其中一个向量向另外一个向量进行投影。操作时候就能得到该平面的一组正交基。

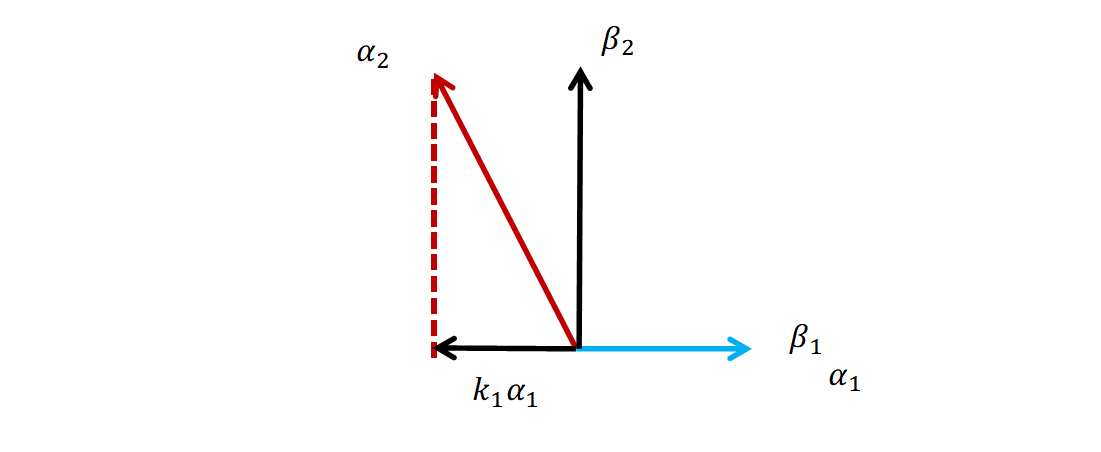
矩阵分解

---

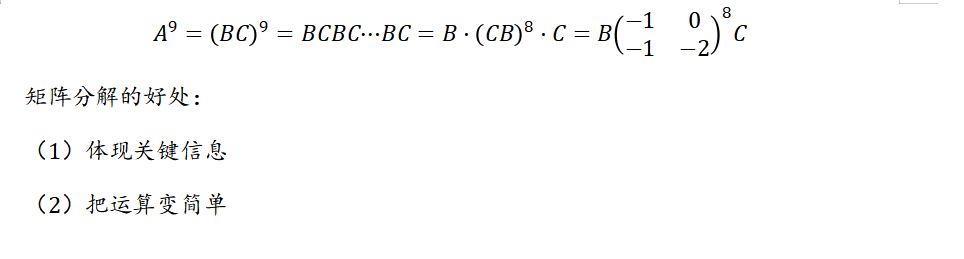
线性方程组

非齐次线性方程组的解

几何角度

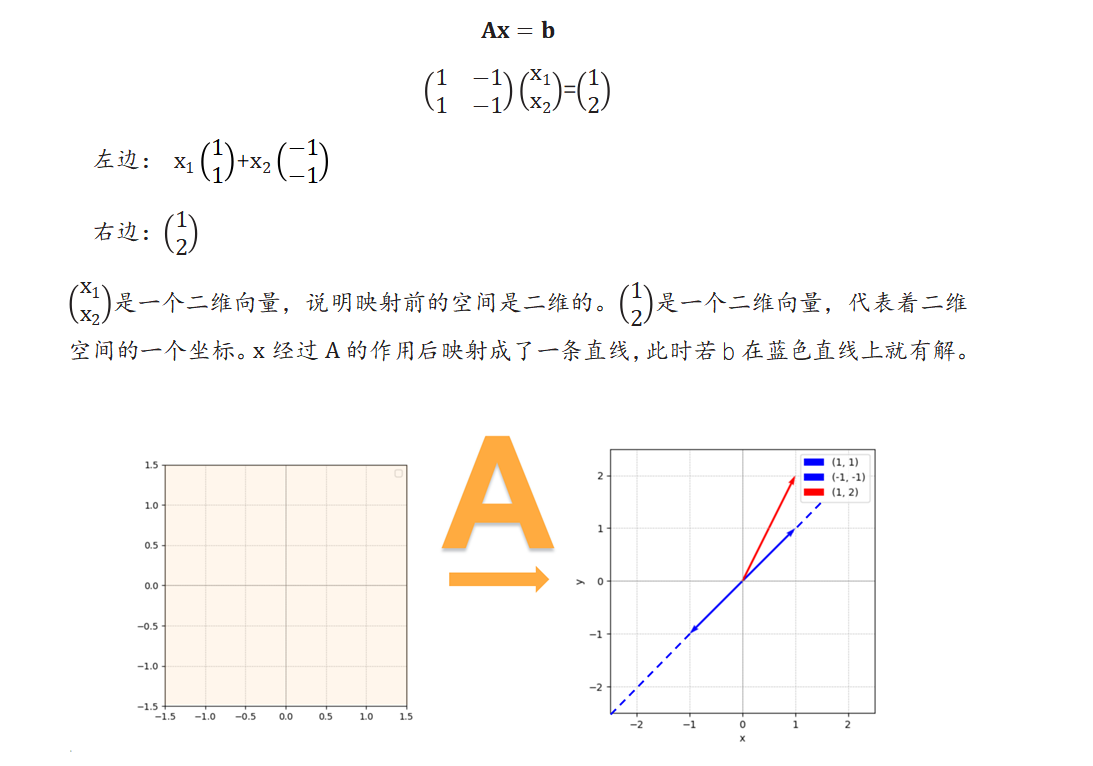
秩的角度

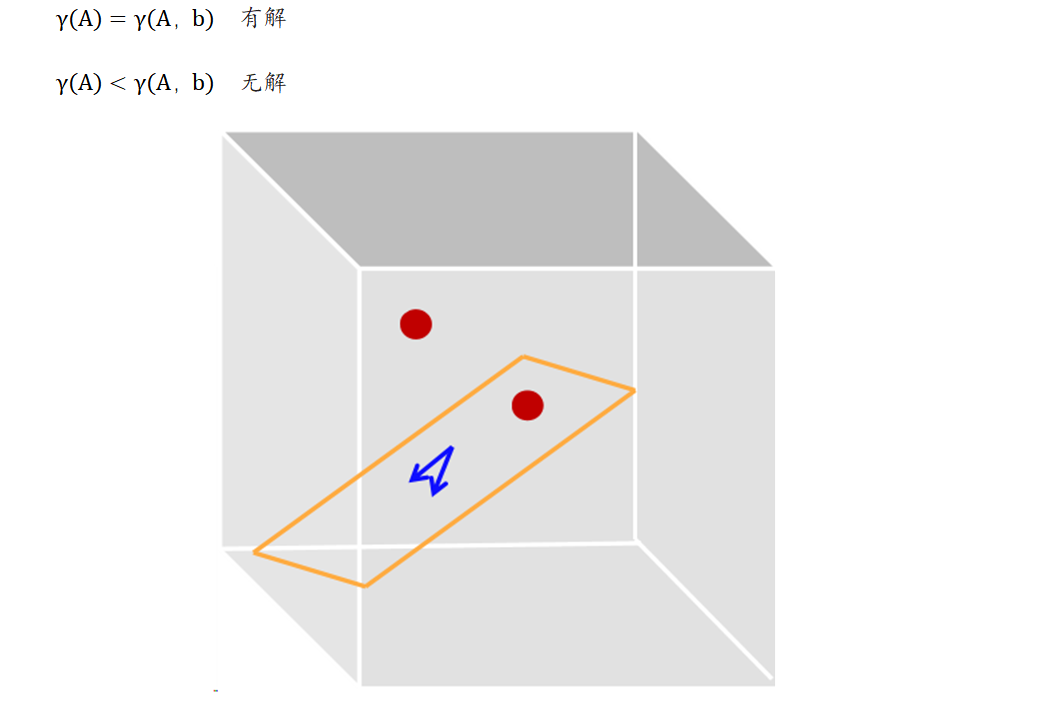
基础解析

基础解析：构成解空间的基

b是在解空间的一个坐标

基础解析的个数

方程组的近似解

---

矩阵的特征值和特征向量

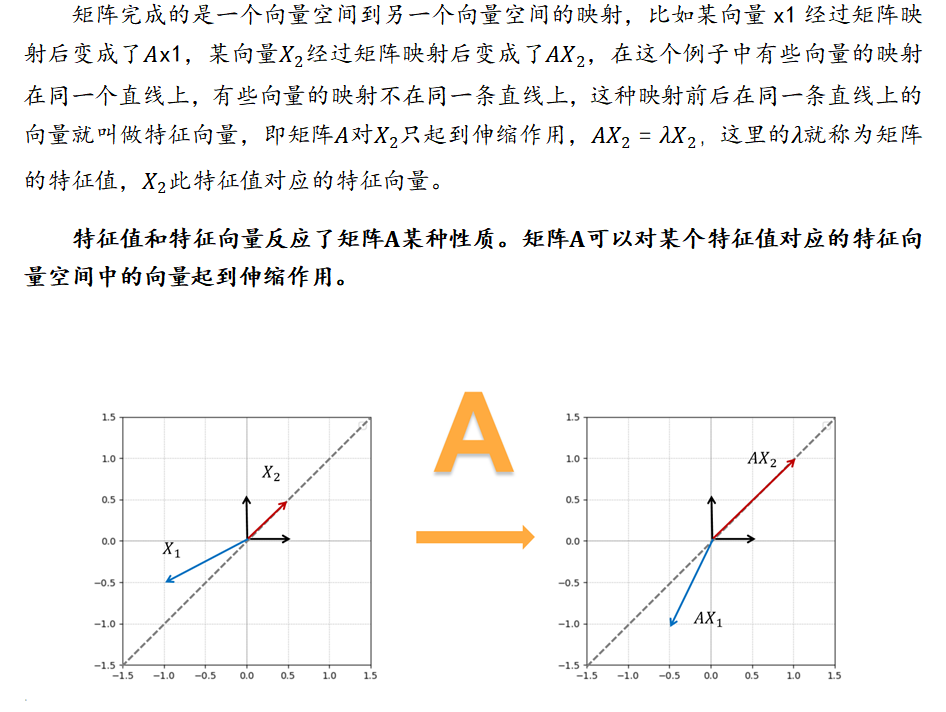
矩阵的特征值和特征向量

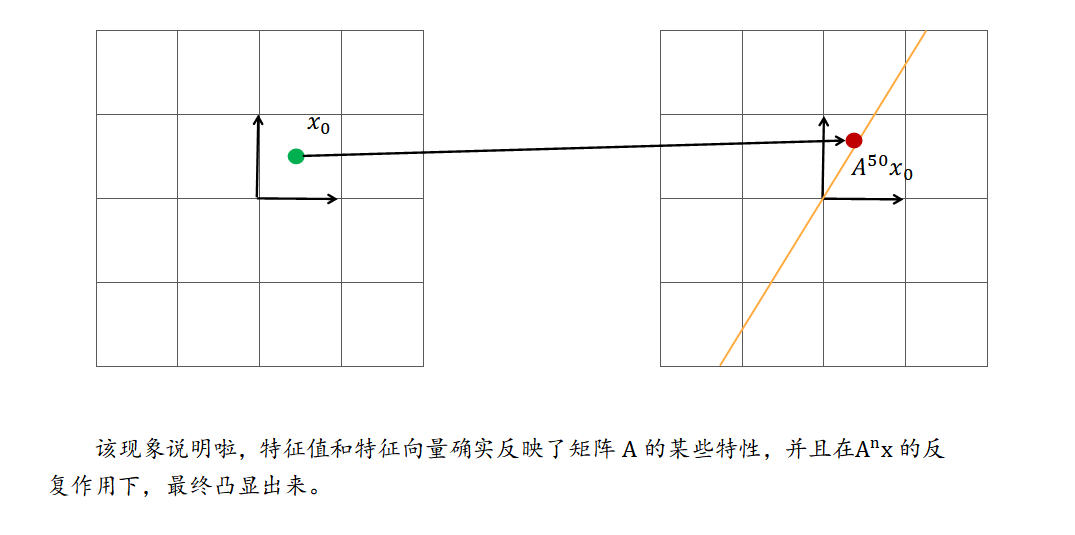
**** 特征值和特征向量反应了矩阵某种性质。矩阵可以对某个特征值对应的****特征向量空间中的向量起到伸缩作用。

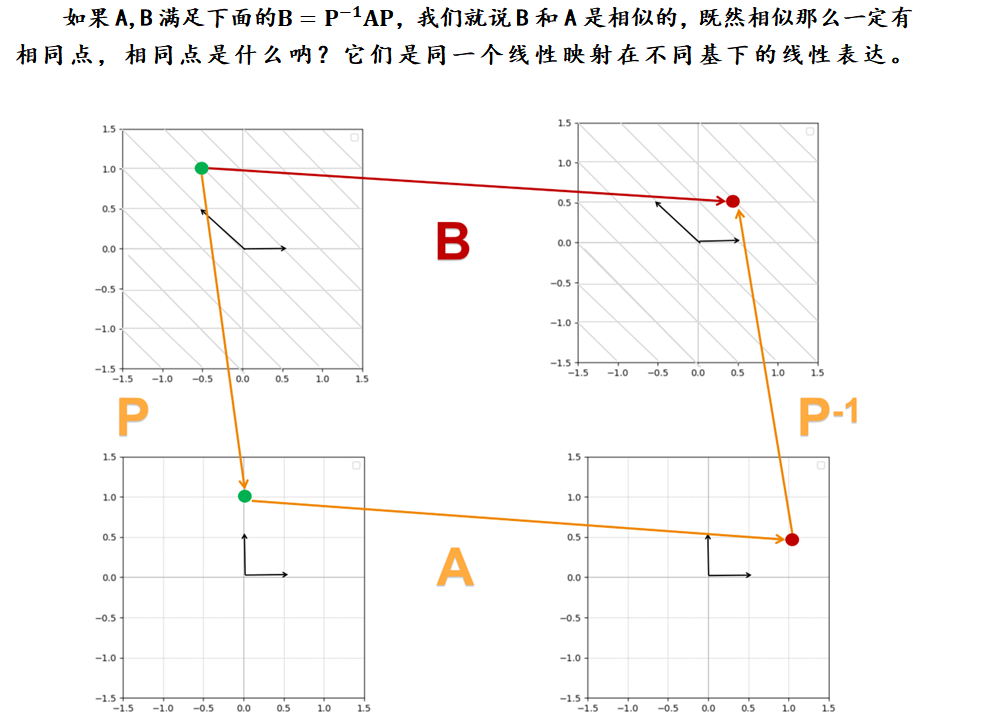
相似矩阵

**** 我们就说B和A是相似的，既然相似那么一定有相同点，相同点是什么呐？****它们是同一个线性映射在不同基下的线性表达。

​​​​​​​相似对角化

---

二次型

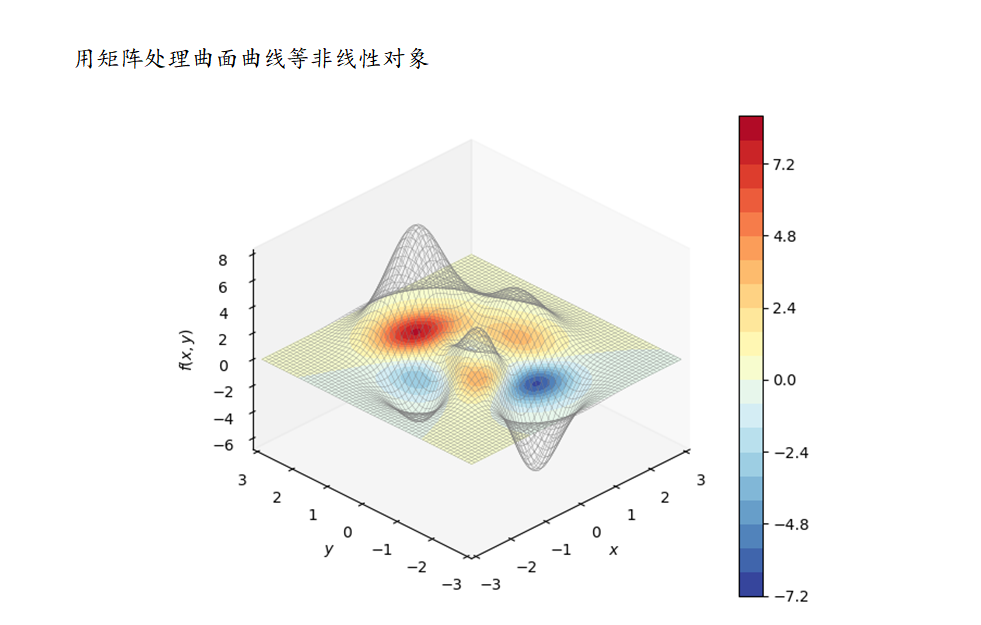
用矩阵处理曲面曲线等非线性对象

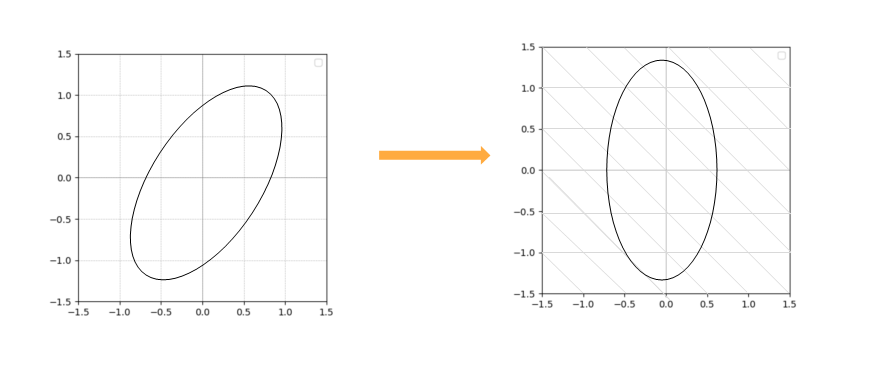
​​​​​​​矩阵合同

同一事物在不同坐标系下的不同形态