密文策略属性基加密(CP-ABE)
在之前的(KP-ABE)中,密文和属性相关联,私钥与访问策略相关联,可以决定能解密的密文,加密者无法控制谁能够访问他加密的数据。在密文策略属性基加密(CP-ABE)中正好与之相反,私钥与属性相关联,密文与访问结构相关联,能够决定拥有哪些属性的用户可以解密密文,这样设置,加密者就能够控制谁有权访问他加密的数据。这与传统的访问控制方法,基于角色的访问控制(RBAC)类似。在CP-ABE中,使用了一种新颖的私钥随机化技术来保证抗共谋性。使用新的两级随机掩蔽的技术。
在CP-ABE中,与密文相关联的访问结构也被构造为访问树。其中树的内部节点都是一个阈值门,由其子节点和阈值描述。如果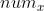是其子节点的个数,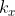是其阈值,则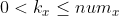。与门和或门都可以被构造成阈值门,当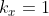时,就是或门,当时就是与门。叶子节点与属性相关联,由属性值和阈值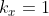描述。为了便于使用访问数,还定义了一些函数。parent(x)表示树中节点的父节点。att(x)表示与树中叶节点相关联的属性,只有x节点是叶节点时才定义该函数。对于节点的子节点来说,需要对子节点进行编号,index(x)返回子节点的索引值。
满足访问树。令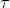为根为r的访问树,用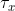表示以节点x为根的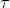的子树,因此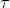与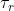是一样的,如果一组属性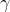满足访问树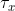,我们将其表示为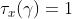,递归计算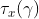。如果x是非叶子节点,则计算节点x的子节点的值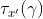,当至少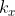个子节点返回1时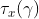返回1。如果x是叶子节点,当且仅当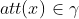时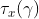返回1。
CP-ABE过程
G0是素数阶p的双线性群,g是G0的生成元。此外e: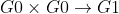表示双线性映射。安全参数k将确定群的大小。同时为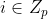和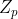中元素的集合S定义拉格朗日系数:
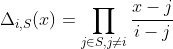
另外使用一个哈希函数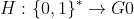,将其建模为随机预言机,功能会将任意描述为二进制字符串的属性映射到随机群元素。构造如下:
Setup:选择一个具有生成元g的素数阶p的双线性群G0。接下来选择两个随机指数,公钥公布如下:
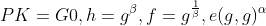
主密钥MK为:,这里的f仅仅用来委托。
Encrypt(PK,M,):加密算法将在访问结构
下加密消息M。首先为树
中的每个节点选择一个多项式
。(包括叶子节点),这些多项式从根节点R开始以一种自顶向下的方式选择。
对于树中的每个节点x,设置多项式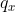的次数比节点阈值少一,也就是。首先,从根节点R开始,随机选择一个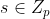并且设置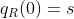,然后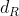次多项式的其他点完全随机的选取。对于任意的其他节点x,设置,其他点随机选择来定义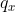。令Y为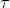中叶子节点集合,然后通过给出的访问结构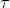构造密文如下:
**KeyGen(MK,S):**密钥生成算法以一组属性S作为输入,并输出以该集合表示的密钥。算法首先选择一个随机,然后为每个属性
选择随机
,然后计算密钥为:
Delegate(SK,):委托算法接受一个密钥SK,用于一组属性S和令一组属性
,其中
。密钥的形式为
,算法选择一个随机
和
,然后它创造一个新的密钥:
得到的密钥是集合
的密钥。因为这个算法重新随机化了密钥,所以委托密钥等同于直接从权威机构得到一个。
**Decrypt(CT,SK):**解密过程是一个递归过程。我们首先定义一个递归算法DecryptNode(CT,SK,x),以密文,一个与一组属性关联的私钥SK和
中的一个节点为输入。如果节点x为叶子节点,令i=att(x),定义如下:如果
,则
DecryptNode(CT,SK,x) =
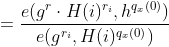
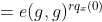
如果,定义DecryptNode(CT,SK,x) =
。
当x不是叶子节点时,DecryptNode(CT,SK,x) 算法过程如下:对于x的所有子节点z,调用DecryptNode(E,D,z)并保存输出为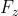,令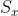为任意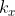大小的子节点z的集合,使得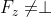,如果这样的集合不存在,则节点不满足,函数返回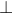。否则,计算如下:
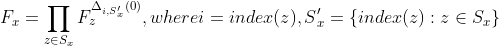

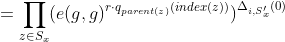
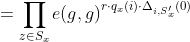
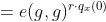
返回结果,如果这个树被集合S满足,设置A=DecryptNode(CT,SK,r)=。这个算法通过计算
,这样就得到了明文信息。
参考文献
BETHENCOURT J, SAHAI A, WATERS B. Ciphertext-policy attribute-based encryption[C]
版权归原作者 lntuzgm 所有, 如有侵权,请联系我们删除。