传送门⏬⏬⏬
前言
你好啊,既然你点进来了,那就进来学点知识??蓝桥杯将至,来学点常考算法吧,不多bb开🚀
另外,欢迎关注我的专栏,用心写题解

🌟一、如何理解“图”?
图
Graph是一种非线性表数据结构,和树比起来,这是一种更加复杂的
非线性表结构。我们知道,树中的元素我们称为
节点,图中的元素我们就叫作顶点(
vertex)。从我画的图中可以看出来,图中的一个顶点可以与任意其他顶点建立连接关系。我们把这种建立的关系叫作边(
edge),另外,
树是一种
特殊的图, 是无环的, 并且连同。
✨1、无向图
- 边是没有方向的
a——b相当于 可以a->b b->a,所以无向图是一种特殊的有向图(有向图开俩边就是无向图)。 - 比如,社交网络,就是一个非常典型的图结构。我们就拿微信举例子吧。我们可以把每个用户看作一个
顶点。如果两个用户之间互加好友,那就在两者之间建立一条边。所以,整个微信的好友关系就可以用一图的表示:如何存储微博、微信等社交网络中的好友关系?张图来表示。其中,每个用户有多少个好友,对应到图中,就叫作顶点的度(degree),就是跟顶点相连接的边的条数。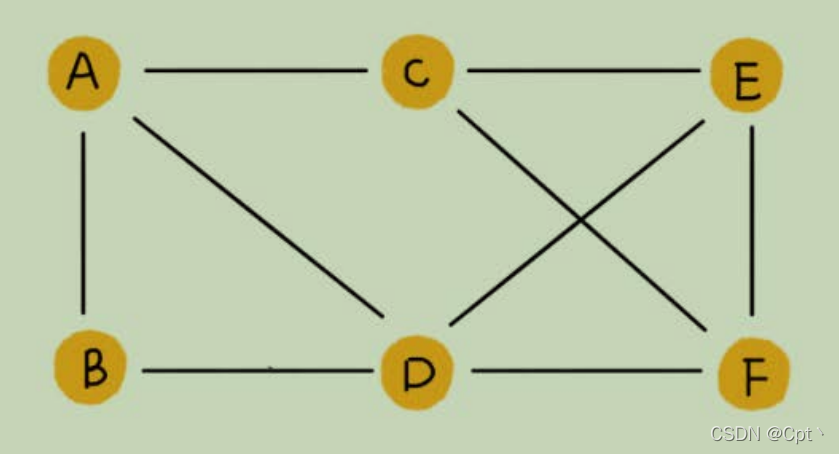
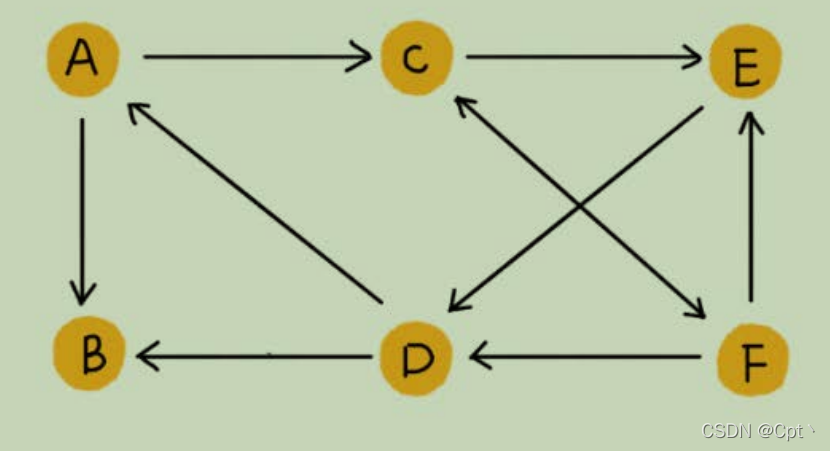
✨2、有向图
- 边是有方向的
A—>B是加上了方向性 (学这个就行)。 - 以微博举例,微博允许单向关注,也就是说,用户A关注了用户B,但用户B可以不关注用户A。那我们如何用图来表示这种单向的社交关系呢?我们可以把刚刚讲的图结构稍微改造一下,引入边的“方向”的概念。如果用户A关注了用户B,我们就在图中画一条从A到B的带箭头的边,来表示边的方向。如果用户A和用户B互相关注了,那我们就画一条从A指向B的边,再画一条从B指向A的边。我们把这种边有方向的图叫作“
有向图”。
✨3、带权图(weighted graph)
- 在带权图中,每条边都有一个权重(
weight),我们可以通过这个权重来表示QQ好友间的亲密度。
✨4、小总结
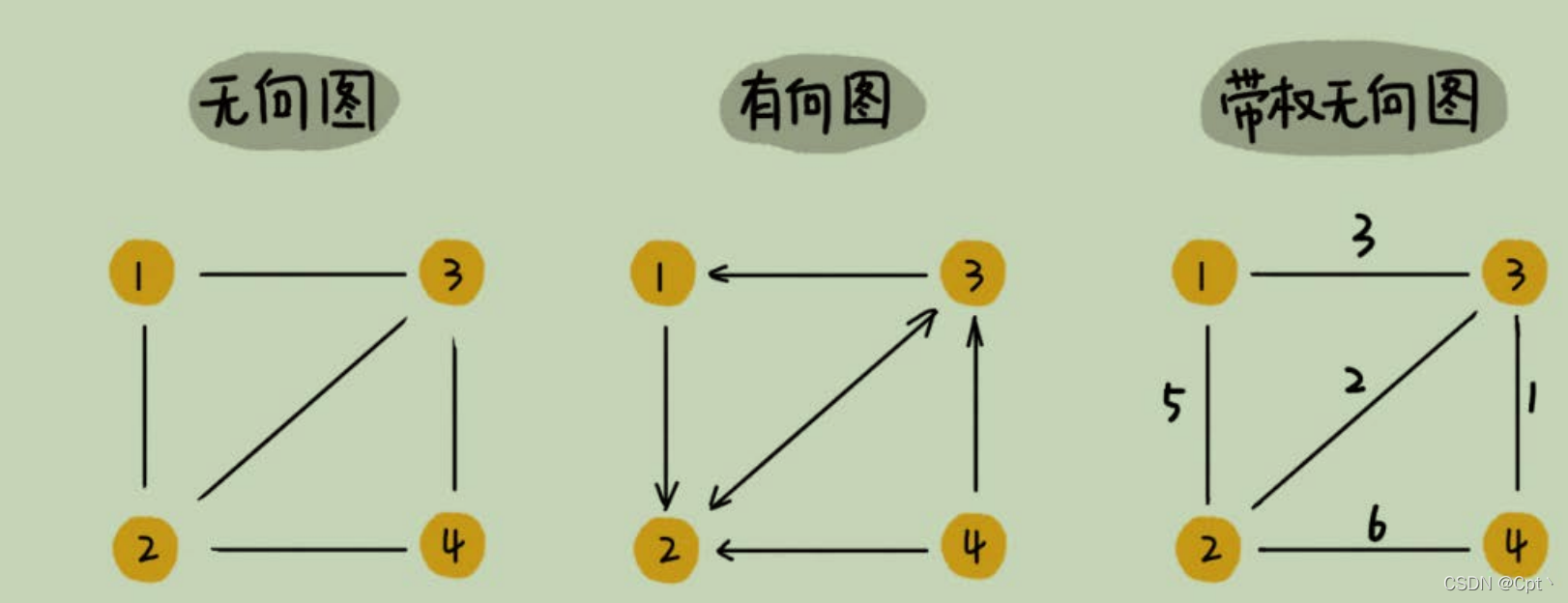
关于图的概念比较多,我今天也只是介绍了几个常用的,理解起来都不复杂,不知道你都掌握了没有?掌握了图的概念之后,我们再来看下,如何在内存中存储图这种数据结构呢?
🌟二、图的存储方式
1、邻接矩阵存储方法
g[x][y]
(二维数组) 空间复杂度 n2 适合稠密图。
缺点:只能保留一条最短的边,如果我们存储的是稀疏图(
Sparse Matrix
),也就是说,顶点很多,但每个顶点的边并不多,那邻接矩阵的存储方法就更加浪费空间了。比如微信有好几亿的用户,对应到图上就是好几亿的顶点。但是每个用户的好友并不会很多,一般也就三五百个而已。如果我们用邻接矩阵来存储,那绝大部分的存储空间都被浪费了。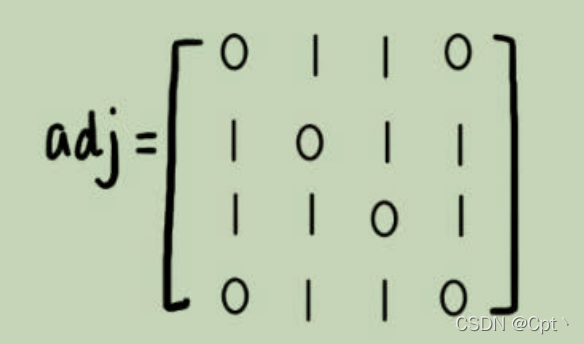
✨2、邻接表存储方法
用的比较多,相当于n个单链表,与哈希的
拉链法
相似,每一个结点开了一个单链表 ,存储可以到的距离为一的点。图中画的是一个
有向图
的
邻接表
存储方式,每个顶点对应的链表里面,存储的是指向的顶点。对于无向图来说,只需要再反方向加一条边即可。eg.第一个单链表存储的是 和
h[1]
可以到的距离为
1
的点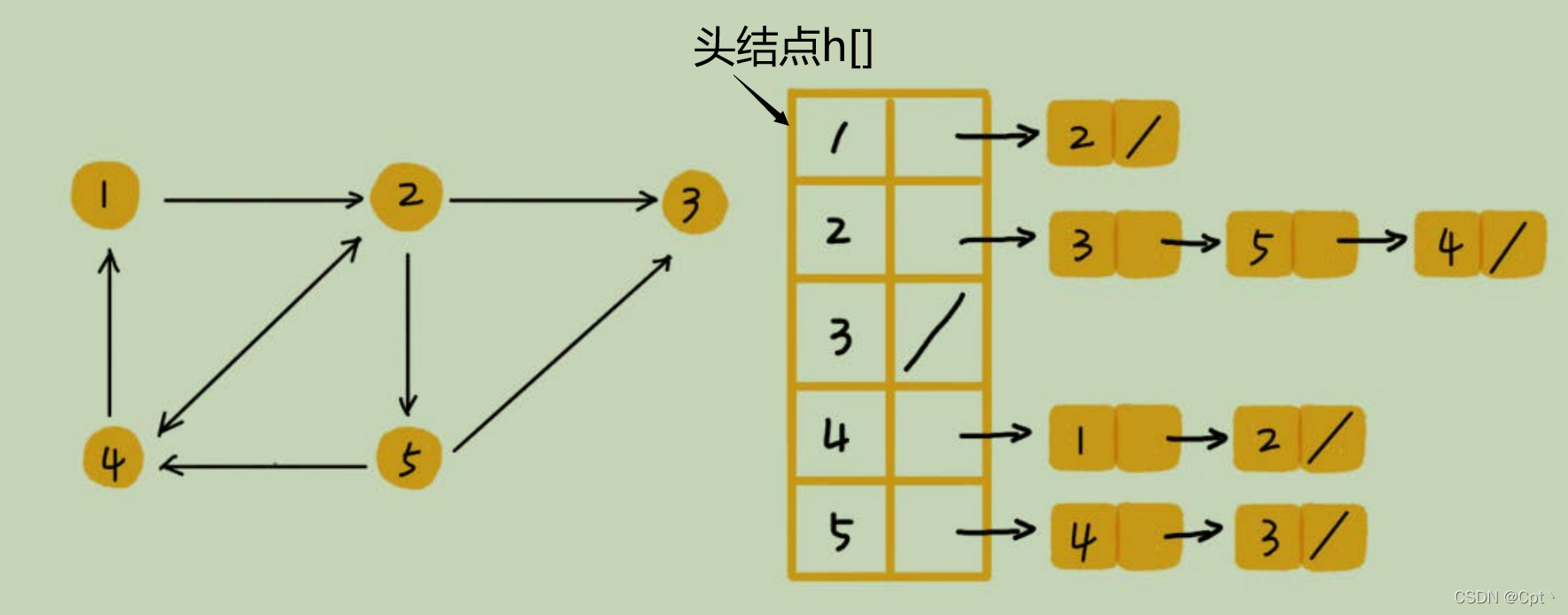
✨3、对比总结
邻接矩阵邻接表优点存储方式简单、直接 、方便计算。邻接表存储起来比较节省空间缺点比较浪费存储空间使用起来就比较耗时间(查询麻烦)
🌟三、总结DFS和BFS
DFSBFS数据结构
O(n)
O(2n) 这里的 n:深度时间复杂度
stack
栈
queue
队列区别不具备最短性最短路
先上图

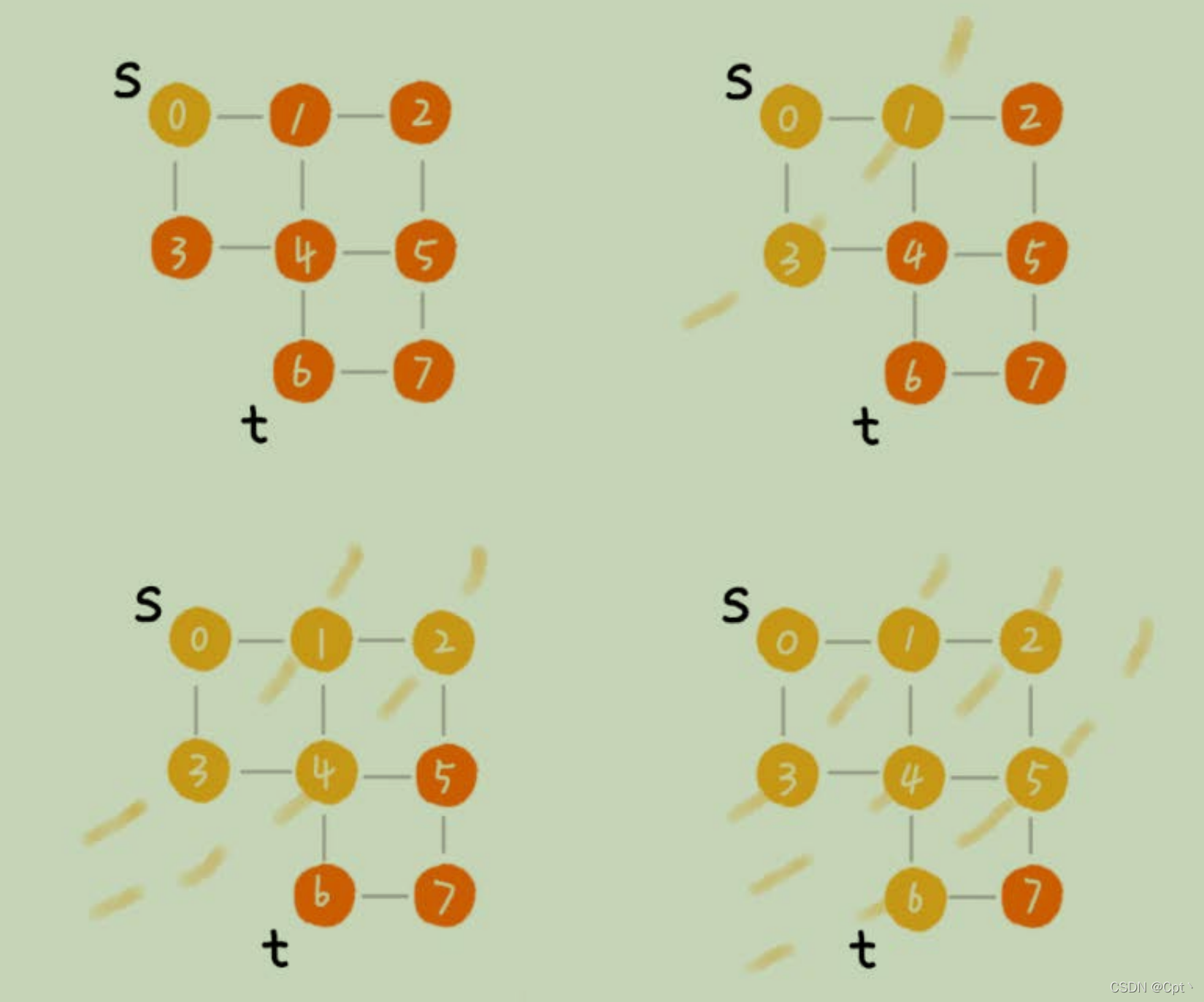
- DFS[暴搜]:从头走到尾,如果没找到,就一层一层地返回重新找另一个子链,然后再继续深入找,左边找完找右边。
- 我的另一篇暴搜文章(建议收藏) DFS “深搜”排列数字+八皇后问题 ( 图解+详细注释 )

- BFS:它其实就是一种“地毯式”层层推进的搜索策略,即先查找离起始顶点最近的,然后是次近的,依次往外搜索。
我的另一篇文章BFS 走迷宫 八数码
🌟四、实战题目
✨1、DFS遍历图的模板
- 这是为数不多DFS的模板
图的边怎么构建?本质就是单链表的插入 。不懂可以看我这篇文章 文章链接 点击跳转
e[idx]= x, ne[idx]= ne[k], ne[k]= idx++;
首先是赋值,然后改变指针方向,再让原来的元素直线自己,最后移动下标继续进行操作 最重要的是
ne[idx] = ne[k]
,
ne[k] = idx
这俩步的操作 次序一定不能颠倒 下面是我画的图方便理解

图解遍历路径 ↓

- 可以发现是一层一层搜索
算法模板↓
#include<iostream>#include<cstring>#include<algorithm>usingnamespace std;constint N =100010, M = N *2;int n, m;int h[N], e[M], ne[M], idx;bool st[N];//标记每个走过的点,防止二次遍历//构建边voidadd(int a,int b){
e[idx]= b, h[idx]= ne[a], h[a]= idx++;}//暴搜 核心模板voiddfs(int u){
st[u]=true;for(int i = h[u]; i !=-1; i = ne[i]){//遍历每个根节点int j = e[i];if(!st[j]){dfs(j);}}}intmain(){memset(h,-1,sizeof h);//初始化每个点为空[含义:没有来过]dfs(1);return0;}
✨2、Acwing.846. 树的重心 [DFS搜索树]
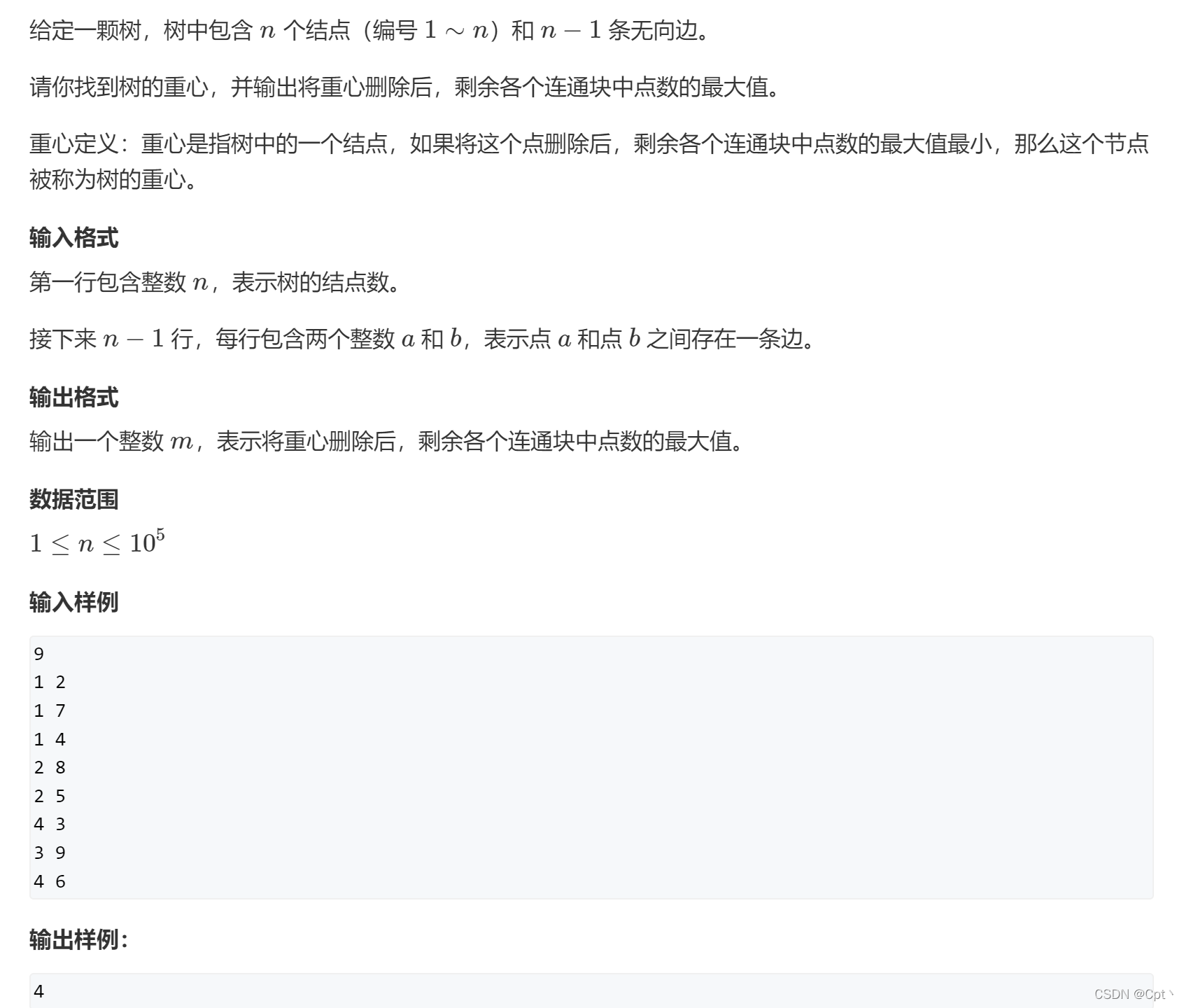
题目
思路
- 树的重心定义:重心是指树中的一个结点,如果将这个点删除后,剩余各个连通块中点数的最大值最小,那么这个节点被称为树的重心。
题目解读:结合下图一起看,图中画的是输入样例的
树
,也可以理解为一个具有
无向边
且没有环结构的图。就是删除每个节点,然后记录每个节点的连通块的最大值
MAX
。然后遍历比较每个节点,更新每个节点的连通块的
最大值MAX
的
MIN
,建议
断句理解
. 比如下图俩个例子 第一个删除
节点2
后,最大连通块为
6
,此时
res2=6
,
ans=(ans=N,res2)=6
。第二个删除
节点4
后,此时
res4=5
记录当前,
ans=min(ans=6,res4)=5



代码
#include<iostream>#include<algorithm>#include<cstring>usingnamespace std;constint N =100010, M = N *2;//无向图,所以每个节点至多对应2n-2条边int h[N];//队头int e[M];//存储元素的值int ne[M];//存储列表的next值 int idx;//单链表指针int n,m;int ans = N;//保存答案 N为题目范围 MAXbool st[N];//记录节点是否被访问过,用于遍历每个点//图结点的边 [原理和单链表的插入一样] voidadd(int a,int b){
e[idx]= b, ne[idx]= h[a], h[a]= idx++;}//以u为跟的子树中点的数量[包括u节点]intdfs(int u){
st[u]=true;//标记一下[表示已经搜过] 保证每个点只遍历一次int sum =1;//存储以u为根的树的节点数(包括u )如图中的4号节点int res =0;//存储 删掉某个节点之后,最大的连通子图节点数 for(int i = h[u]; i !=-1;i = ne[i]){//遍历每个点int j = e[i];if(!st[j]){int s =dfs(j);// u节点的单棵子树节点数 如图中size值
res =max(res, s);// 保存最大联通子图的节点数
sum += s;//以j为根的树 的节点数}}
res =max(res, n - sum);// 选择u节点为重心,最大的 连通子图节点数
ans =min(ans, res);//最小的最大联通子图的节点数return sum;}intmain(){
cin >> n >> m;memset(h,-1,sizeof h);// 所有点赋值为空[-1]// 树中是不存在环的,对于有n个节点的树,必定是n-1条边for(int i =0; i < n -1; i ++){int a, b;
cin >> a >> b;add(a, b),add(b, a);//构造无向边}dfs(1);//哪个点开始搜都行 因为每个点都要遍历
cout << ans << endl;return0;}
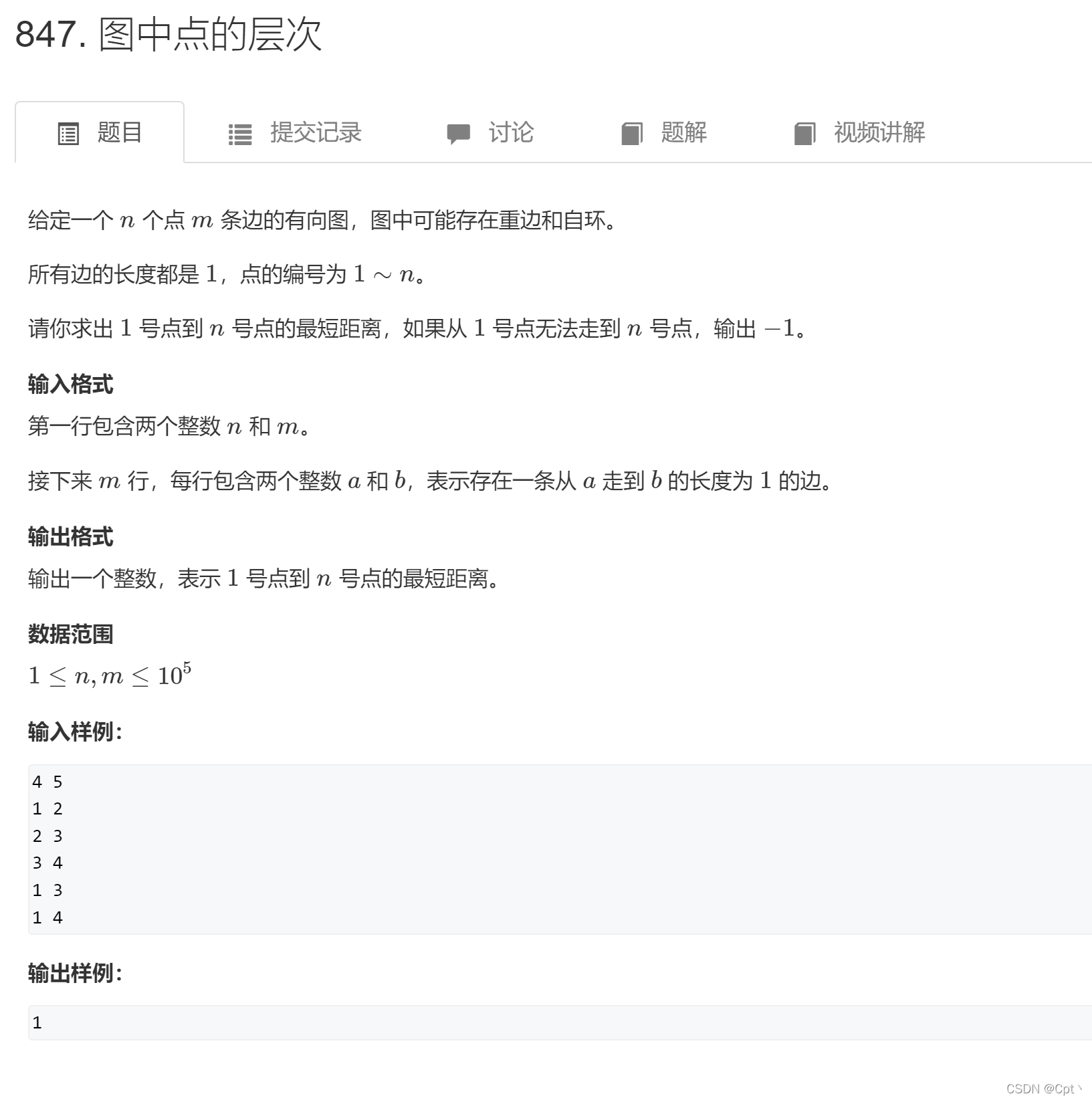
✨3、Acwing847. 图中点的层次 [BFS]
题目
图中 所有边都是1 由此可以BFS来做
重边 :俩条边指向一个结点
自环 : 结点自己指向自己
思路

核心
for(int i = h[t]; i !=-1; i = ne[i])// ne[i]上的点都是与i节点距离为1的点{int j = e[i];// 点的值if(d[j]==-1)// 如果j没有被遍历过{
d[j]= d[t]+1;// 因为路径长度都是1,上一个点的长度加上1即可
q.push(j);// 将j加到队列中}}
代码
不懂参考文章BFS 走迷宫 八数码
#include<iostream>#include<algorithm>#include<cstring>#include<queue>#include<cstdio>usingnamespace std;constint N =100010;int n, m;int h[N], e[N], ne[N], idx;int d[N], q[N];//构建边voidadd(int a,int b){
e[idx]= b, ne[idx]= h[a], h[a]= idx ++;}intbfs(int n){memset(d,-1,sizeof d);
queue<int> q;
d[1]=0;
q.push(1);//加入起点while(!q.empty()){int t = q.front();// t 保存队头
q.pop();//弹出队头元素for(int i = h[t]; i !=-1; i = ne[i])// ne[i]上的点都是与i节点距离为1的点{int j = e[i];// e[i]保存下标if(d[j]==-1)// 如果j没有被遍历过{
d[j]= d[t]+1;// 因为路径长度都是1,所以直接在上一步的基础上加上1即可
q.push(j);// 将j加到队列中}}}return d[n];// 返回的d[n]即是节点1到节点n的距离}intmain(){
cin >> n >> m;memset(h,-1,sizeof h);for(int i =0; i < m; i ++){int a, b;scanf("%d%d",&a,&b);add(a, b);}
cout <<bfs(n)<< endl;return0;}
✨4、拓扑排序
知识点
拓扑排序知识点:拓扑排序本身就是基于有向无环图的一个算法,同时,有向无环图也被称为拓扑图。有向性上面说了。环是什么?像a->b->c->a这样,就是环,图中一旦出现环,拓扑排序就无法工作了。
出度 一个点指向其他点的边的数量。
入度 一个点被指向的边的数量。
拓扑序列:只有从前指向后面的边,没有从后面指向前面的边,如图:下面这种就不是拓扑序列 ↓
- 结论:只有带环的才有指向后面的边,由此有向无环图也被称为拓扑图。
题目描述
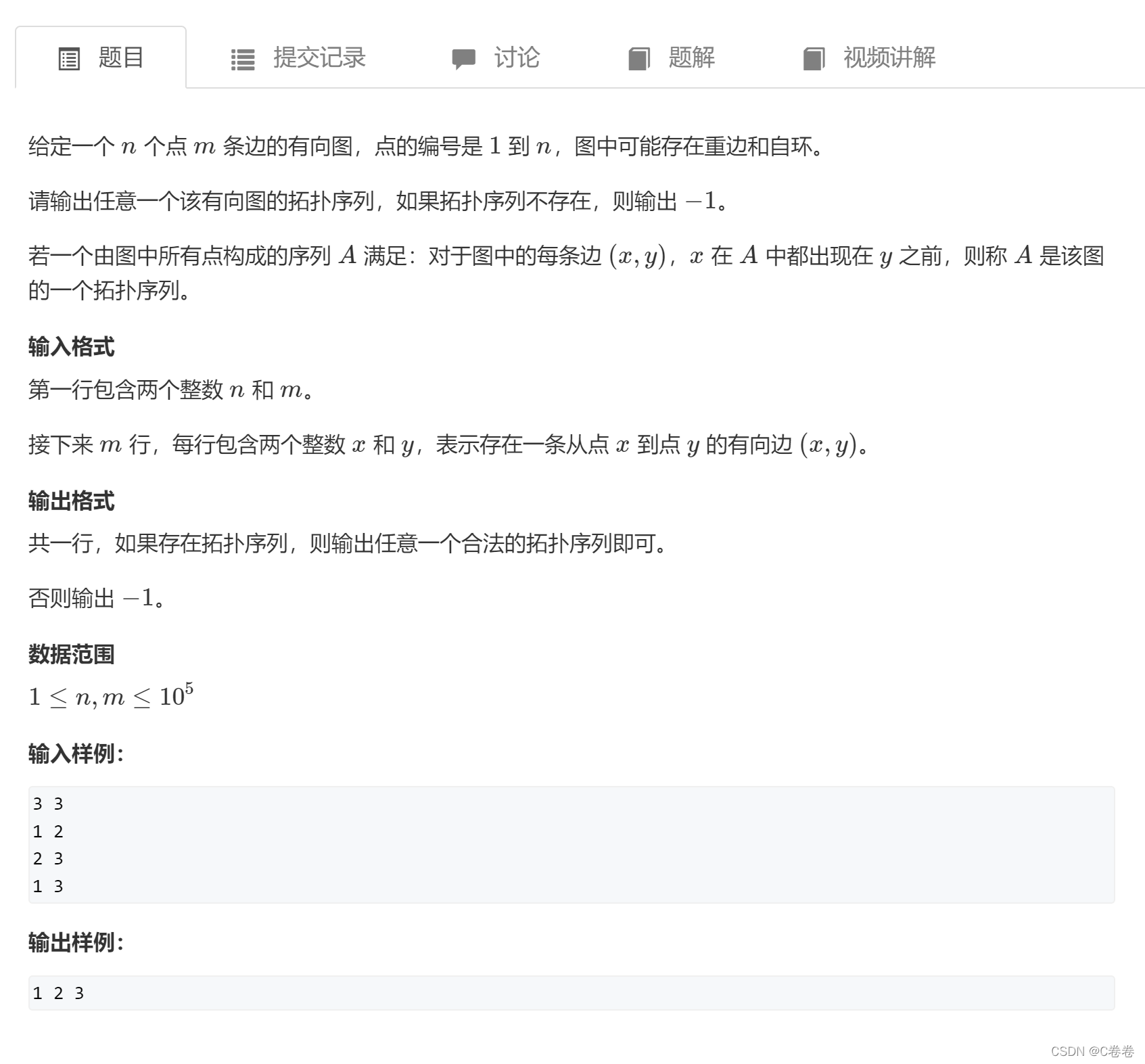
思路
遍历寻找到起点,然后删去该点,最后遍历点所有出边。
AC代码
#include<iostream>#include<cstring>#include<queue>#include<algorithm>usingnamespace std;constint N =100010;int e[N], ne[N], h[N], idx, n, m;int d[N];//存储每个元素的入度int top[N];//拓扑排列的序列int cnt =1;//记录拓扑元素的个数//邻接链表存储voidadd(int a,int b){
e[idx]= b, ne[idx]= h[a], h[a]= idx++;}//判断是否符合拓扑序列booltopsort(){
queue<int> q;int t;for(int i =1; i <=n; i ++){if(d[i]==0){//遍历寻找起点[入度为0的点]
q.push(i);}}while(!q.empty()){
t = q.front();//每次取出队列的首部
top[cnt ++]= t;//加入到 拓扑序列中
q.pop();//删除这个点for(int i = h[t]; i !=-1;i = ne[i]){int j = e[i];
d[j]--;// j的入度-1if(d[j]==0){//如果j入度为0,加入队列当中
q.push(j);}}}//当所以点都入队,cnt ==nif(cnt < n){return0;}else{return1;}}intmain(){int a, b;
cin >> n >> m;memset(h,-1,sizeof h);while(m --){
cin >> a >> b;add(a, b);
d[b]++;//a——>b ,b的入度+1}if(topsort()==0){
cout <<"-1";}else{for(int i =1; i <= n;++ i){
cout << top[i]<<" ";}}return0;}
🌟五、结尾
感谢你能看完, 如有错误欢迎评论指正,这篇文章创作用时
5小时,字数
1w,如果对你有帮助的话,点个赞鼓励下, 谢啦!!☆⌒(*^-゜)v
版权归原作者 C卷卷 所有, 如有侵权,请联系我们删除。




