一. 图解二叉树的深度优先搜索
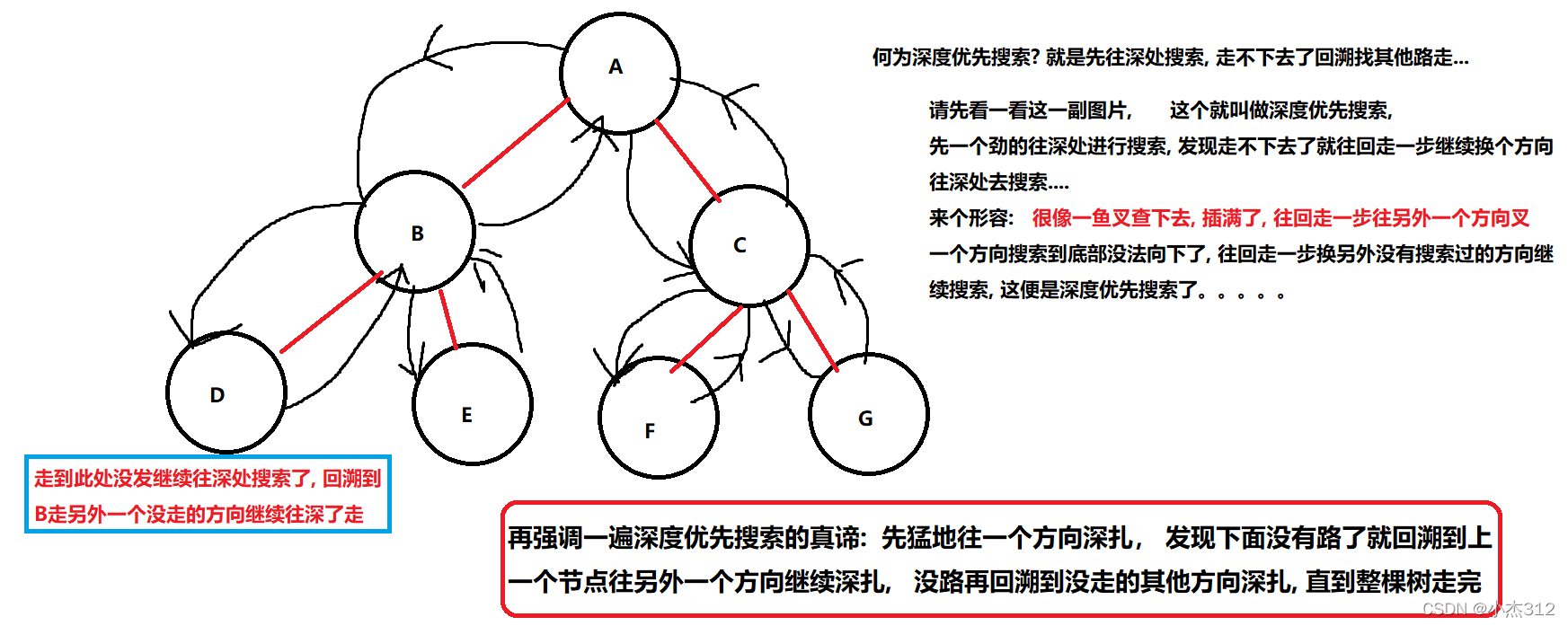
- 然后提到深度优先搜索必然是离不开三种二叉树的深搜遍历方式的:
- 前序遍历: 根部 左子树 右子树
- 中序遍历:左子树 根部 右子树
- 后序遍历: 左子树 右子树 根部
到了此处 大家都很气愤了, 在学校里的时候三种遍历方式就没完全搞透澈过, 每次都是跟着感觉走, 写代码的话就也只是会写递归, 不过不怕了, 图形结合 递归代码, 咱走一走:

- 好了艰难的地方过去了, 其实上述告知的不是一个具体的万能公式啥的, 也不是要你记住就OK了, 如果是大佬就不用看了, 因为大佬堪称人肉递归机器. 但是咱初学者要是真想好好理解递归函数一定要自己这样按照短小的代码展开去感受一下, 真正的身临其境的走一遭, 真的会有一番不同的感受的 (真心的一点小建议)
- **好了还是把刚刚的问题解决了, 三种遍历方式咋看都没说: (要是上述的这些过程都看懂了这个也就是一个小意思了) **
- 有一个技巧是三个三个节点的来看, 但是 要清楚的留空, 此处的技巧就在留下空格
- 前序举个例子: 根部 左子树 右子树
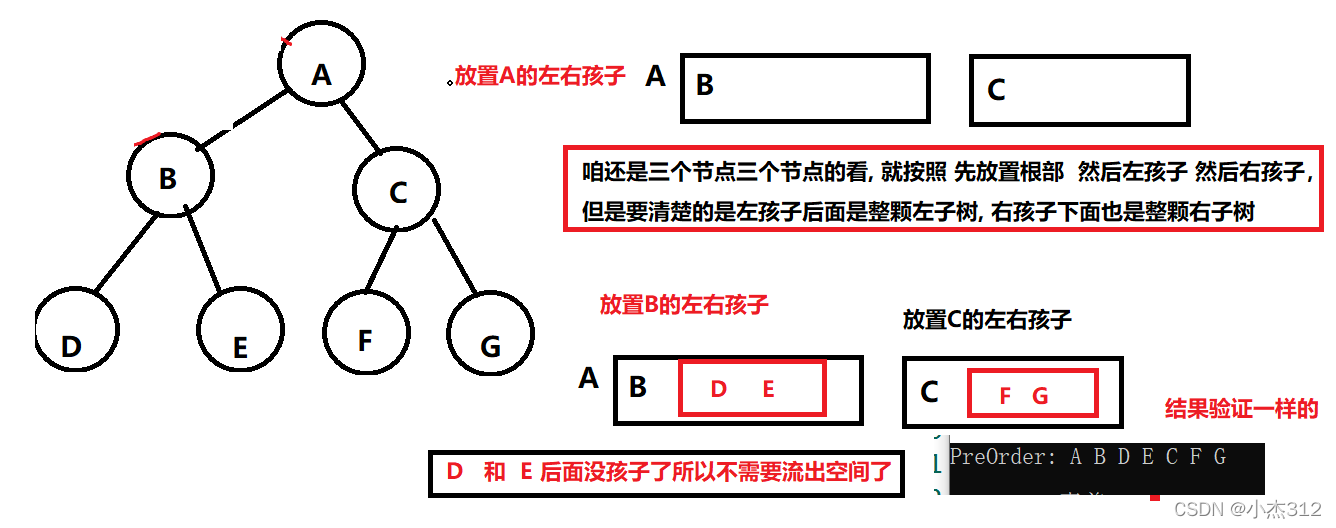
- 至此, 大家都是完全知道咋办了, 我觉着另外两种以聪明的大家肯定可以自行脑补了
二. 二叉树的广度优先搜索 (层序遍历)
- 二叉树的广度优先搜索也称层序遍历就非常的简单了.... 人如其名(当然不是人) 遍历方式如同意思(就是一层一层的遍历二叉树, 一层一层的扫)
- 思考一下???? 我想实现的是一层一层的扫描? 如何可以办到?
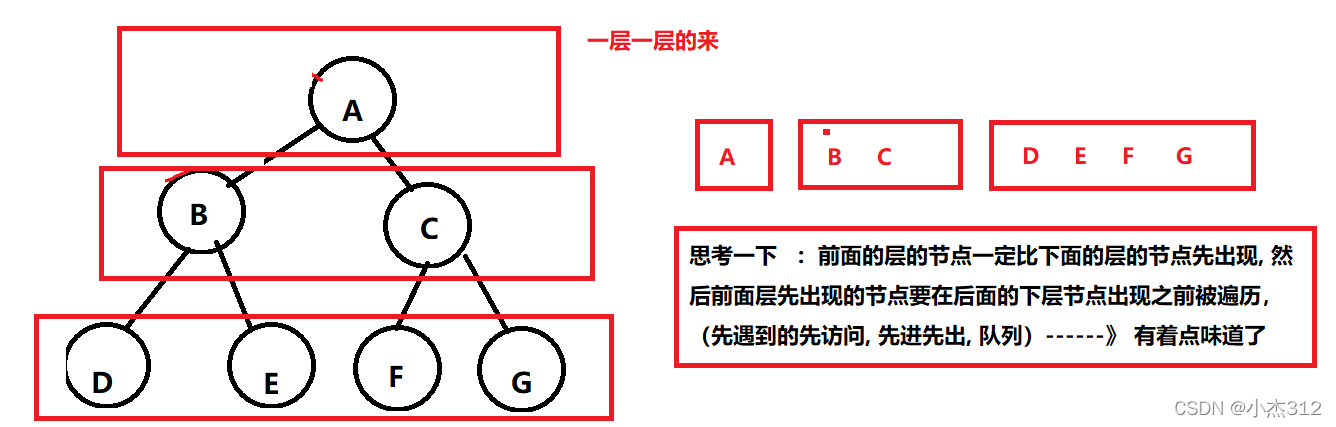
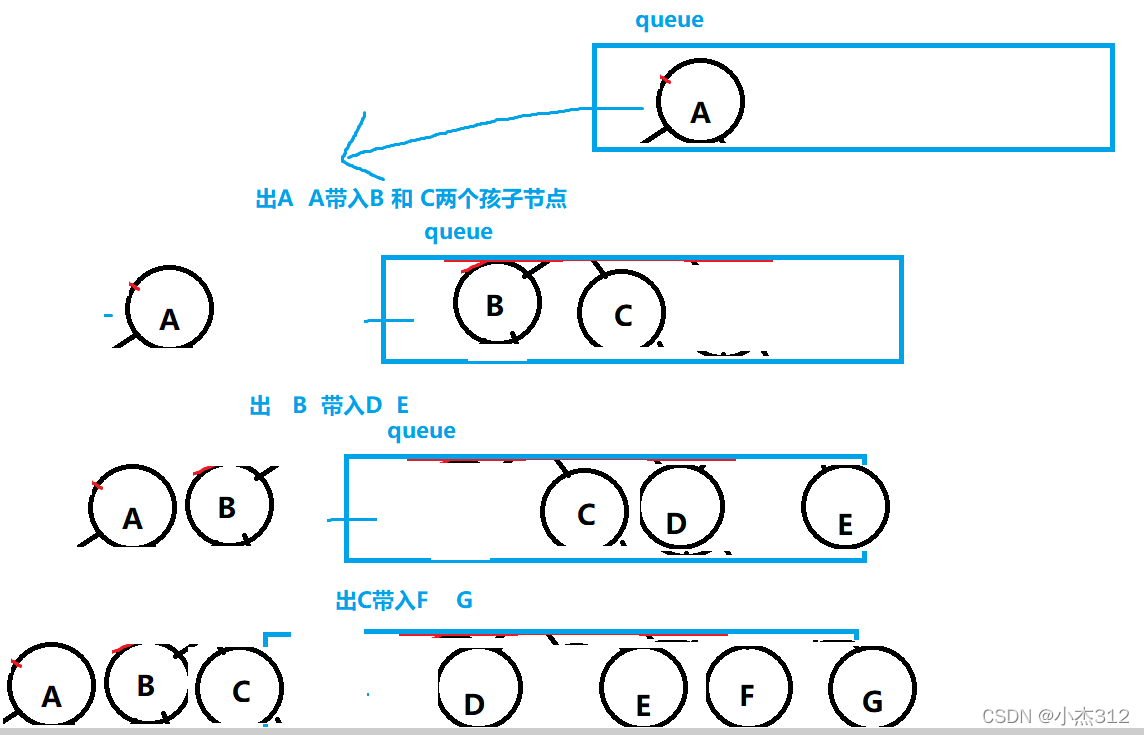
- 总结道理: 利用队列这个数据结构, 出上一层元素, 出的时候用上一层带入下一层的元数就OK了 代码模型如下
//版本1
void LevelOrder(Node* root) {
queue<Node*> q;
q.push(root);
while (!q.empty()) {
Node* pCur = q.front();//拿出上一层的节点
cout << pCur->val << " ";//打印
q.pop();//弹出本层节点
if (pCur->left) q.push(pCur->left);
if (pCur->right) q.push(pCur->right);
//入下一层的节点
}
}
//版本2:
void LevelOrder2(Node* root) {
queue<Node*> q;
q.push(root);
while (!q.empty()) {
int n = q.size();//计算本层节点数目
for (int i = 0; i < n; ++i) {//除去本层,入下一层
Node* pCur = q.front();
cout << pCur->val << " ";
q.pop();
if (pCur->left) q.push(pCur->left);
if (pCur->right) q.push(pCur->right);
}
}
}
三. 打开LeetCode 撸起来
- 二叉树的前序遍历
给你二叉树的根节点
root
,返回它节点值的 前序* *遍历。
这个题目使用递归的话及其的简单, 就是cout << "根部"; 递归遍历Func(左子树), 递归Func(右子树).... 只不过此处的cout需要改成 push_back 存储在vector中作为结果
写递归三要素: 边界条件 递归统一的操作是什么 返回值 (写递归的时候一定向着这三点上面思考)
class Solution {
void PreOrder(TreeNode* root, vector<int>& ans) {
//if (!root) return ; !root 等效rooot == nullptr
if (root == nullptr) return ;//终点(边界)
//中间操作
ans.push_back(root->val);
PreOrder(root->left, ans);
PreOrder(root->right, ans);
return ;//返回值
}
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int > ans;//存储遍历结果
ans.clear();//清空容器
PreOrder(root, ans);
return ans;
}
};
小爽一把: 咱自己按照上述的方式去写如下两道题目:咱都知道写起来很简单, 但是养成写递归的习惯, 习惯性的思考三要素. 对于递归的培养还是蛮有好处的)
二叉树的中序遍历
二叉树的后序遍历
**使用递归写上述题目确实非常的简单, 仅仅算得上是简单题目, 这个是因为具体的深入不了的回溯过程 + 系统栈 都是递归函数帮助我们隐形的处理了, 所以上述过程变得及其简单好写, 弊端, 不便于对于整个遍历过程的思考, **
好了咱自己模拟系统栈的回溯, 用栈辅助实现递归一般的深入和回溯. 还是哪个整体的思路, 先一条路往深了走, 走不动咱就回溯一步. 往其他路走....
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int > ans;//存储遍历结果
ans.clear();//清空容器
stack<TreeNode*> st;
TreeNode* p = root;
while (p || !st.empty()) {
//循环结束条件 p空 + st空
while (p) {
ans.push_back(p->val);//遍历根部
st.push(p);//入栈根部,为了回溯
p = p->left;//左深入
}
//自此处, p深入到NULL,需要回溯一步走另一边
//栈顶存储的是前面的节点,回溯就是往回走,取栈顶
TreeNode* oldP = st.top();//回溯节点
st.pop();//弹出
p = oldP->right;//搜索另一边
}
return ans;
}
};
**跟着上述思路走, 完全小小的修改便可以写出中序遍历了, **
**但是后序遍历没那么简单,写非递归? 后序 左子树 右子树 根部. (why?) 存在两次回溯, 如何判断是第一次回溯还是第二次回溯, 这个算是一个思考题了, 说实话不好想, 大佬除外, 突破点:标记, 代码我附在下面大家可以简单的思考一下如果感兴趣的...(大佬路过就行) **
思考这样一个问题. 每一次从右边回溯上去到之前的根部节点, 你都会思考我刚刚是从左边上来的还是右边上来的? 如果是左边继续走右, 如果是右边, 遍历根部
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int > ans;//存储结果
ans.clear();
stack<TreeNode*> st;
TreeNode* p = root;
TreeNode* usedP = nullptr;//标记刚刚走过
while (p || !st.empty()) {
//先深入左边
while (p) {
st.push(p);//存储根部为了后序回溯
p = p->left;//深入左
//对比前序不能入根部?
//左子树 右子树 根部(你懂)
}
//至此说明p走到空
TreeNode* oldP = st.top();//回溯
//思考, 我是有没有走过右边, 是从右边还是左边上来的?
if (oldP->right && oldP->right != usedP) {
p = oldP->right;//深入右
} else {
//左子树走了, 右子树是空或者走了, 入根部
ans.push_back(oldP->val);
usedP = oldP;//走过, 标记走过
st.pop();
}
}
return ans;
}
};
去掉冗余注释版本: 会的人看的
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int > ans;//存储结果
ans.clear();
stack<TreeNode*> st;
TreeNode* p = root;
TreeNode* usedP = nullptr;//标记刚刚走过
while (p || !st.empty()) {
//先深入左边
while (p) {
st.push(p);//存储根部为了后序回溯
p = p->left;//深入左
}
TreeNode* oldP = st.top();//回溯
if (oldP->right && oldP->right != usedP) {
p = oldP->right;
} else {
ans.push_back(oldP->val);
usedP = oldP;
st.pop();
}
}
return ans;
}
};
至此, 咱多少被刚刚的后序非递归搞得可能有点小晕晕的, 没事,层序简单呀.... (层序就是纯模板, 打10个小意思)
- 层序需要大家多练, 一定开始多练, 后面自然用的出神入化(做个面试二叉树不小case)
- 二叉树的层序遍历
给你二叉树的根节点
root,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int > > ans;
if (root == nullptr) return ans;//防空
vector<int> path;//记录每一层结果
queue<TreeNode*> q;
q.push(root);
TreeNode* pCur;
//要求? 一层一层的访问节点, 使用写法2吧.
while (!q.empty()) {
int n = q.size();//本层节点数目
for (int i = 0; i < n; ++i) {
pCur = q.front();
q.pop();
path.push_back(pCur->val);
if (pCur->left) q.push(pCur->left);
if (pCur->right) q.push(pCur->right);
}
ans.push_back(path);//入上一层
path.clear();//清空继续存下一层
}
return ans;
}
};
??? 你说层序就层序, 我的面子哪里放, 可以递归吗请问?可以深搜解决吗.让递归函数去帮我们干这个苦活重活
- 思路: 想一想? 使用层序的好处是一层一层的做的处理, 我们只要按照它的要求存储序列就是它 首先只要能遍历完树然后按照层序序列存储不也还是层序序列吗....
- 深搜不一样可以遍历整颗树吗? 只不过常规的深搜少了一个条件, 不清楚当前遍历的节点是那一层的, 所以给深搜 + deep层数参数便可解决这个问题了。
class Solution {
void dfs(vector<vector<int > >& ans, TreeNode* root, int deep) {
if (root == nullptr) return ; //边界条件
if (ans.size() == deep) ans.push_back(vector<int >());//塞入空一位数组
ans[deep].push_back(root->val);
dfs(ans, root->left, deep + 1);
dfs(ans, root->right, deep + 1);
return ;//返回值
}
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int > > ans;
ans.clear();
dfs(ans, root, 0);//0起始层数
return ans;
}
};
- 然后授人以鱼不如授人以渔。。。 后序还有很多题目, 希望大家能按照上述两种方式都尝试练习, 几乎都是上述的模板... 题目链接附在如下:
二叉树的层序遍历 II
二叉树的锯齿形层序遍历
面试题32 - I. 从上到下打印二叉树
- N 叉树的前序遍历
然后如下的就是一些经典性的题目. 二叉树的最近公共祖先 + 建立二叉树 (又特别是建立二叉树,其实算是蛮不好处理的题目)
- 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。 说俗点, 就是p 和 q 向上看找第一个合在一起的地方
- **咋做? 典型的递归, 然后嘞. 层序根本不好使, 这个肯定是利用好回溯过程中进行判断返回节点. **
- 首先的第一步找到 p 节点 和 q 节点不断地向上回溯
- 然后一直向上回溯判断, 首先思考第一个问题, 走到了 公共节点地时候 p 和 q 肯定都是已经找到了地, 一定确定地是q 和 p 都找到了, 这个题目, 我们需要使用后序遍历..... 为啥?
- 因为你得先确定你的左子树和右子树中分别 有 p 和 q 然后这个根部才是公共祖先... 所以你必须先获取左右子树地情况. 然后判断根部是不是所需地最近公共祖先, 至此思路明了了
- return val : 找到地p q 或者是 root 最近公共祖先
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root == NULL) return NULL;
TreeNode* l = lowestCommonAncestor(root->left, p, q);
TreeNode* r = lowestCommonAncestor(root->right, p, q);
//获知了左右子树地信息了
//开始判断
if (root == p || root == q) return root;
if (l && r) return root;//左右子树中有p 和 q return 祖先
if (l) return l;//返回找到地结果
if (r) return r;//返回找到地结果
return NULL;
}
};
- 从前序与中序遍历序列构造二叉树
题目意思就超级简单了, 就是给你两个序列 一个 前序遍历结果序列 另外一个是中序遍历序列, 然后让你构造出来这个二叉树....
- 前序: 根部 左子树 右子树 : 所以前序过来是每一个根部
- 中序 左子树 根部 右子树 : 可以根据前序地根部分开左右子树区间
- 请问咋做, 上述说的超级清楚了 根据前序地根部不停地分割中序地左右区间, 左右区间分别就是左子树和右子树, 然后递归式建立二叉树就OK了
class Solution {
unordered_map<int, int> ind;//采取一个技巧, 映射下标位置
//[l, mid) mid, (mid, r)
TreeNode* BuildTree(vector<int>& preorder, vector<int>& inorder, int& rooti, int l, int r) {
if (l >= r) {
rooti -= 1;//回溯
return nullptr;//l 和 r 之间没有元素
}
TreeNode* root = new TreeNode(preorder[rooti]);
int mid = ind[preorder[rooti]];
//[l, r)
root->left = BuildTree(preorder, inorder, ++rooti, l, mid);
root->right = BuildTree(preorder, inorder, ++rooti, mid + 1, r);
return root;
}
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
for (int i = 0; i < inorder.size(); ++i) {
ind[inorder[i]] = i;
}
int i = 0;
//至此获取到中序地值index地映射键值对map
//[0, inorder.size()) [l, r)
return BuildTree(preorder, inorder, i, 0, inorder.size());
}
};
- 前序遍历构造二叉搜索树
思路: 因为是二叉搜索树 所以是满足 左子树 < 根部 < 右子树地
前序 根部 左子树 右子树 所以 根部 比所有的左子树节点都大, 于是可以根据这个特性找到左右子树地分界位置, 分割出来左右子树, 然后建立二叉树搜索树...
转换为中序遍历建立二叉搜索树地形式, 将前序序列转换为中序序列建立二叉搜索树即可....
因为你可以区分出根 左子树区间 右子树区间...
class Solution {
TreeNode* BuildTree(vector<int>& preorder, int l, int r) {
if (l >= r) return nullptr;
TreeNode* root = new TreeNode(preorder[l]);
int mid = l + 1;
while (mid < r && root->val > preorder[mid]) ++mid;
root->left = BuildTree(preorder, l + 1, mid);
root->right = BuildTree(preorder, mid, r);
return root;
}
public:
TreeNode* bstFromPreorder(vector<int>& preorder) {
return BuildTree(preorder, 0, preorder.size());
}
};
现在差不多大体上大家应该对于建树也有点感觉了, 主要是使用递归处理 + 找到左右子树地分割线, 至此再附上链接几条大家可以去做做
从中序与后序遍历序列构造二叉树
最大二叉树
四, 总结(外加建议)
- 本文主要介绍了二叉树地深度优先搜索和广度优先搜索, 以图解理论结合实践地形式拖出. 之后我会不停地跟新自己对于算法和数据结构地浅显见解, 希望大家多多支持谢谢
- 还有一个小小地建议就是学数据结构和算法必须得学练并举... (小杰的小小经验)不练习很多时候对于结构和算法的理解会下降和遗忘... 做过的题目需要反复做, 仅仅对于面试经典题目而言, 最好每一次得出不同的感受
- 深度优先搜索本质: 先往深处搜索,走不动了回溯上去搜索另外没有搜索的方向
- 广度优先搜索层序遍历(一层一层的)地毯式搜索. 之后可以介绍更多, 它比较适合找最短路径
- 然后是建树关键 分割区间递归建树
- 最终感谢大家对小杰的支持,感谢CSDN让身处各地的大家通过一片片博文相知相识, 谢谢群里各位志同道合朋友的大力支持, 小杰真心的感谢大家.. 希望大家一起加油,共同进步
版权归原作者 小杰312 所有, 如有侵权,请联系我们删除。