广义学习矢量量化(Generalized Learning Vector Quantization,GLVQ)是一种基于原型的分类算法,用于将输入数据分配到先前定义的类别中。GLVQ是LVQ(Learning Vector Quantization)的一种扩展形式,LVQ在特征空间中利用一组代表性原型来对输入数据进行分类。
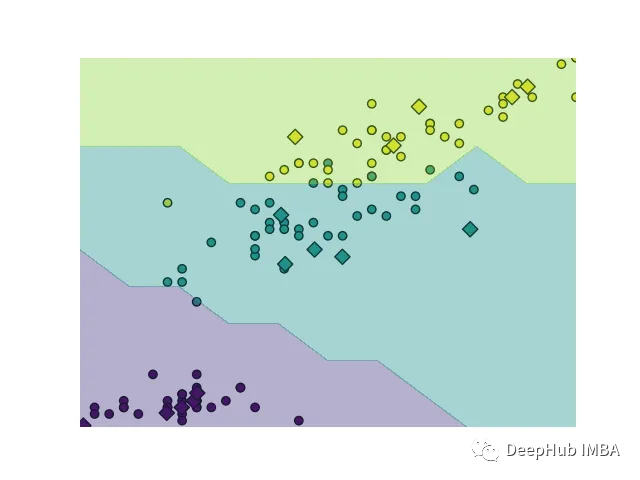
GLVQ
GLVQ是一种监督学习算法,属于学习矢量量化(LVQ)算法的范畴。LVQ算法是一种基于原型的分类算法,它根据类与代表每个类的一组原型(也称为范例或参考向量)的距离将类分配给数据点。GLVQ通过允许类之间更灵活的决策边界来扩展LVQ,这在数据类不可线性可分时尤其有用。
GLVQ与LVQ的主要区别在于,GLVQ将类别之间的区别表示为权重矩阵,而不是在特征空间中使用距离度量。GLVQ中的权重矩阵可以从数据中学习,使得分类器可以自适应地调整权重,以便更好地区分不同的类别。此外,GLVQ还可以使用非线性映射将输入数据投影到一个新的特征空间中,这样就可以更好地处理非线性分类问题。
GLVQ可以应用于各种分类问题,尤其是在需要处理高维度数据和非线性分类问题的情况下。以下是GLVQ的一些具体应用:
- 模式识别:GLVQ可以用于模式识别,例如人脸识别、手写数字识别、图像分类等。通过将输入数据映射到原型向量空间,GLVQ可以在原型向量之间寻找最佳匹配,实现分类的目的。
- 计算机视觉:GLVQ可以用于计算机视觉领域的各种任务,例如目标检测、图像分割、物体跟踪等。GLVQ可以将输入数据投影到一个低维空间,然后利用原型向量来分类数据。
- 生物医学工程:GLVQ可以应用于生物医学工程领域,例如基因表达数据分析、心电信号分类等。GLVQ可以用于分析和分类复杂的生物医学数据,帮助研究人员识别疾病的特征并做出预测。
- 自然语言处理:GLVQ可以用于自然语言处理领域,例如文本分类、情感分析、机器翻译等。GLVQ可以通过将文本数据映射到原型向量空间来实现文本分类和情感分析等任务。
GLVQ的目标是学习一个权重矩阵,该矩阵将输入向量映射到类别空间中的向量。该映射可以通过最小化一个目标函数来学习,该目标函数将输入向量映射到它们正确的类别向量的距离最小化。
具体来说,GLVQ学习一个由原型向量组成的集合,其中每个原型向量代表一个类别。对于一个新的输入向量,GLVQ计算该向量与每个原型向量之间的距离,并将其分配给与其距离最近的原型向量所代表的类别。GLVQ可以根据分类的准确性调整原型向量的位置,以便更好地区分不同的类别。
GLVQ有许多变体,包括适应性GLVQ(Adaptive GLVQ)、增强型GLVQ(Enhanced GLVQ)和概率GLVQ(Probabilistic GLVQ),它们在权重矩阵的形式、目标函数和学习算法等方面有所不同。这些变体广泛应用于模式识别、计算机视觉、语音识别等领域,以解决各种分类问题。
数学解释和python代码
广义学习矢量量化(Generalized Learning Vector Quantization,GLVQ)的分类原理是将输入样本映射到原型向量上,并找到距离最近的原型向量,将输入样本分配给与其距离最近的原型向量所代表的类别。

在 GLVQ 中,每个类别都有一个原型向量,表示该类别在特征空间中的位置。输入样本与原型向量之间的距离可以通过欧几里得距离或曼哈顿距离等度量方法来计算。下图为二元分类的代码
# normalize the data
defnormalization(self, input_data):
minimum=np.amin(input_data, axis=0)
maximum=np.amax(input_data, axis=0)
normalized_data= (input_data-minimum)/(maximum-minimum)
returnnormalized_data
# define prototypes
defprt(self, input_data, data_labels, prototype_per_class):
# prototype_labels are
prototype_labels=np.unique(data_labels)
prototype_labels=list(prototype_labels) *prototype_per_class
# prototypes are
prt_labels=np.expand_dims(prototype_labels, axis=1)
expand_dimension=np.expand_dims(np.equal(prt_labels, data_labels),
axis=2)
count=np.count_nonzero(expand_dimension, axis=1)
proto=np.where(expand_dimension, input_data, 0)
prototypes=np.sum(proto, axis=1)/count
self.prt_labels=prototype_labels
returnself.prt_labels, prototypes
# define euclidean distance
defeuclidean_dist(self, input_data, prototypes):
expand_dimension=np.expand_dims(input_data, axis=1)
distance=expand_dimension-prototypes
distance_square=np.square(distance)
sum_distance=np.sum(distance_square, axis=2)
eu_dist=np.sqrt(sum_distance)
returneu_dist
# define d_plus
defdistance_plus(self, data_labels, prototype_labels,
prototypes, eu_dist):
expand_dimension=np.expand_dims(prototype_labels, axis=1)
label_transpose=np.transpose(np.equal(expand_dimension, data_labels))
# distance of matching prototypes
plus_dist=np.where(label_transpose, eu_dist, np.inf)
d_plus=np.min(plus_dist, axis=1)
# index of minimum distance for best matching prototypes
w_plus_index=np.argmin(plus_dist, axis=1)
w_plus=prototypes[w_plus_index]
returnd_plus, w_plus, w_plus_index
# define d_minus
defdistance_minus(self, data_labels, prototype_labels,
prototypes, eu_dist):
expand_dimension=np.expand_dims(prototype_labels, axis=1)
label_transpose=np.transpose(np.not_equal(expand_dimension,
data_labels))
# distance of non matching prototypes
minus_dist=np.where(label_transpose, eu_dist, np.inf)
d_minus=np.min(minus_dist, axis=1)
# index of minimum distance for non best matching prototypes
w_minus_index=np.argmin(minus_dist, axis=1)
w_minus=prototypes[w_minus_index]
returnd_minus, w_minus, w_minus_index

# define classifier function
def classifier_function(self, d_plus, d_minus):
classifier = (d_plus - d_minus) / (d_plus + d_minus)
return classifier
# define sigmoid function
def sigmoid(self, x, beta=10):
return (1/(1 + np.exp(-beta * x)))
GLVQ 将该样本映射到所有原型向量上,并计算每个映射结果与该输入样本的距离。然后GLVQ 将输入样本 x 分类为距离最近的原型向量所代表的类别。

# define delta_w_plus
defchange_in_w_plus(self, input_data, prototypes, lr, classifier,
w_plus, w_plus_index, d_plus, d_minus):
sai= (2) * (d_minus/ (np.square(d_plus+d_minus))) * \
(self.sigmoid(classifier)) * (1-self.sigmoid(classifier))
expand_dimension=np.expand_dims(sai, axis=1)
change_w_plus=expand_dimension* (input_data-w_plus) *lr
# index of w_plus
unique_w_plus_index=np.unique(w_plus_index)
unique_w_plus_index=np.expand_dims(unique_w_plus_index, axis=1)
add_row_change_in_w=np.column_stack((w_plus_index, change_w_plus))
check=np.equal(add_row_change_in_w[:, 0], unique_w_plus_index)
check=np.expand_dims(check, axis=2)
check=np.where(check, change_w_plus, 0)
sum_change_in_w_plus=np.sum(check, axis=1)
returnsum_change_in_w_plus, unique_w_plus_index
# define delta_w_minus
defchange_in_w_minus(self, input_data, prototypes, lr, classifier,
w_minus, w_minus_index, d_plus, d_minus):
sai= (2) * (d_plus/ (np.square(d_plus+d_minus))) * \
(self.sigmoid(classifier)) * (1-self.sigmoid(classifier))
expand_dimension=np.expand_dims(sai, axis=1)
change_w_minus= (expand_dimension) * (input_data-w_minus) *lr
# index of w_minus
unique_w_minus_index=np.unique(w_minus_index)
unique_w_minus_index=np.expand_dims(unique_w_minus_index, axis=1)
add_row_change_in_w=np.column_stack((w_minus_index, change_w_minus))
check=np.equal(add_row_change_in_w[:, 0], unique_w_minus_index)
check=np.expand_dims(check, axis=2)
check=np.where(check, change_w_minus, 0)
sum_change_in_w_minus=np.sum(check, axis=1)
returnsum_change_in_w_minus,
可以使用下面代码绘制数据:
# plot data
defplot(self, input_data, data_labels, prototypes, prototype_labels):
plt.scatter(input_data[:, 0], input_data[:, 2], c=data_labels,
cmap='viridis')
plt.scatter(prototypes[:, 0], prototypes[:, 2], c=prototype_labels,
s=60, marker='D', edgecolor='k')
我们的训练代码如下:
# fit function
deffit(self, input_data, data_labels, learning_rate, epochs):
normalized_data=self.normalization(input_data)
prototype_l, prototypes=self.prt(normalized_data, data_labels,
self.prototype_per_class)
error=np.array([])
plt.subplots(8, 8)
foriinrange(epochs):
eu_dist=self.euclidean_dist(normalized_data, prototypes)
d_plus, w_plus, w_plus_index=self.distance_plus(data_labels,
prototype_l,
prototypes,
eu_dist)
d_minus, w_minus, w_minus_index=self.distance_minus(data_labels,
prototype_l,
prototypes,
eu_dist)
classifier=self.classifier_function(d_plus, d_minus)
sum_change_in_w_plus, unique_w_plus_index=self.change_in_w_plus(
normalized_data, prototypes, learning_rate, classifier,
w_plus, w_plus_index, d_plus, d_minus)
update_w_p=np.add(np.squeeze(
prototypes[unique_w_plus_index]), sum_change_in_w_plus)
np.put_along_axis(prototypes, unique_w_plus_index,
update_w_p, axis=0)
sum_change_in_w_m, unique_w_minus_index=self.change_in_w_minus(
normalized_data, prototypes, learning_rate, classifier,
w_minus, w_minus_index, d_plus, d_minus)
update_w_m=np.subtract(np.squeeze(
prototypes[unique_w_minus_index]), sum_change_in_w_m)
np.put_along_axis(
prototypes, unique_w_minus_index, update_w_m, axis=0)
err=np.sum(self.sigmoid(classifier), axis=0)
change_in_error=0
if (i==0):
change_in_error=0
else:
change_in_error=error[-1] -err
error=np.append(error, err)
print("Epoch : {}, Error : {} Error change : {}".format(
i+1, err, change_in_error))
plt.subplot(1, 2, 1)
self.plot(normalized_data, data_labels, prototypes, prototype_l)
plt.subplot(1, 2, 2)
plt.plot(np.arange(i+1), error, marker="d")
plt.pause(0.5)
plt.show()
accuracy=np.count_nonzero(d_plus<d_minus)
acc=accuracy/len(d_plus) *100
print("accuracy = {}".format(acc))
self.update_prototypes=prototypes
returnself.update_prototypes
GLVQ 的训练过程是通过不断更新原型向量来进行的,这个过程可以迭代多次,直到分类结果收敛或达到指定的迭代次数为止。同时,为了防止过拟合,可以引入正则化项对原型向量的更新进行限制。
GLVQ 的数学解释相对简单,但需要注意的是,不同的距离度量方法、学习率调度方法和正则化项都会对算法的性能产生影响,需要根据具体问题进行选择和调整。
预测数据:
# data predict
defpredict(self, input_value):
input_value=self.normalization(input_value)
prototypes=self.update_prototypes
eu_dist=self.euclidean_dist(input_value, prototypes)
m_d=np.min(eu_dist, axis=1)
expand_dims=np.expand_dims(m_d, axis=1)
ylabel=np.where(np.equal(expand_dims, eu_dist),
self.prt_labels, np.inf)
ylabel=np.min(ylabel, axis=1)
print(ylabel)
returnylabel
需要注意的是,GLVQ 的分类结果不一定是唯一的,因为在一些情况下,输入样本可能与多个原型向量的距离相等。为了解决这个问题,可以引入一些规则来确定分类结果,例如优先将输入样本分配给更接近的原型向量所代表的类别,或根据原型向量所代表的类别的先验概率分布来确定分类结果。
Pytorch实现
上面我们介绍的是python的实现,下面我们尝试使用pytorch来实现这个过程(注意:这里是根据原理编写,不保证100%正确,如果发现问题请留言指出)
在 PyTorch 中实现 GLVQ 的方法,主要分为以下几步:
- 准备数据:需要准备训练集和测试集的数据,并进行数据预处理,例如标准化、归一化等操作,以便进行训练和测试。
- 定义模型:需要定义 GLVQ 模型,包括原型向量、距离度量、更新规则等。在 PyTorch 中,可以通过自定义 nn.Module 类来实现 GLVQ 模型,其中包括前向传播和反向传播的方法。
- 定义损失函数:GLVQ 的损失函数通常采用类间距离最小化和类内距离最大化的原则,可以通过自定义 nn.Module 类来实现 GLVQ 的损失函数,其中包括计算损失值和反向传播的方法。
- 训练模型:需要利用训练集对 GLVQ 模型进行训练,并在测试集上进行测试。在 PyTorch 中,可以使用标准的训练和测试流程来训练和测试 GLVQ 模型。
importtorch
importtorch.nnasnn
classGLVQ(nn.Module):
def__init__(self, num_prototypes, input_size, output_size):
super(GLVQ, self).__init__()
self.num_prototypes=num_prototypes
self.input_size=input_size
self.output_size=output_size
self.prototypes=nn.Parameter(torch.randn(num_prototypes, input_size))
self.output_layer=nn.Linear(num_prototypes, output_size)
defforward(self, x):
distances=torch.cdist(x, self.prototypes)
activations=-distances.pow(2)
outputs=self.output_layer(activations)
returnoutputs
classGLVQLoss(nn.Module):
def__init__(self, prototype_labels, prototype_lambda):
super(GLVQLoss, self).__init__()
self.prototype_labels=prototype_labels
self.prototype_lambda=prototype_lambda
defforward(self, outputs, targets):
distances=torch.cdist(outputs, self.prototype_labels)
class_distances=torch.gather(distances, 1, targets.unsqueeze(1))
other_distances=distances.clone()
other_distances[torch.arange(outputs.size(0)), targets] =float('inf')
other_class_distances, _=other_distances.min(1)
loss=torch.mean(class_distances-other_class_distances+self.prototype_lambda*distances.pow(2))
returnloss
# Training
model=GLVQ(num_prototypes=10, input_size=784, output_size=10)
criterion=GLVQLoss(prototype_labels=torch.tensor([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]), prototype_lambda=0.1)
optimizer=torch.optim.SGD(model.parameters(), lr=0.01)
forepochinrange(10):
fori, (inputs, labels) inenumerate(train_loader):
optimizer.zero_grad()
outputs=model(inputs.view(inputs.size(0), -1))
loss=criterion(outputs, labels)
loss.backward()
上述代码实现了一个 GLVQ 模型,其中包含了一个原型向量矩阵 W,每一行表示一个类别的原型向量。训练过程中,输入样本 x 通过计算与每个类别的原型向量之间的距离来进行分类,并将其分配给与其距离最近的原型向量所代表的类别。然后,根据分类结果和样本真实标签之间的误差来更新原型向量,使其向输入样本的方向移动。这样,通过不断更新原型向量,GLVQ 可以学习到特征空间中不同类别之间的边界,并用于分类新的输入样本。
主要说明下GLVQLoss :具体而言,假设输入样本 x 分配给类别 c_{min},则 GLVQ 损失可以表示为:
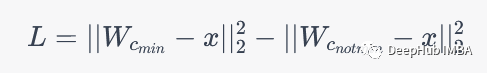
其中 W_{c_{min}} 和 W_{c_{not min}} 分别表示输入样本 x 分配给的类别和未分配给的其他类别的原型向量,||\cdot||_2 表示欧几里得范数。该损失表示了输入样本 x 与其正确类别原型向量之间的距离与其他类别原型向量之间距离之差,即正确类别的原型向量应该更接近输入样本 x。GLVQLoss 是一个带有动态原型向量矩阵的损失函数,它可以根据输入样本和当前的原型向量矩阵来计算损失,并使用梯度下降算法来更新原型向量。
总结
综上所述,广义学习向量量化(GLVQ)是一种强大而灵活的基于原型的分类算法,可以处理非线性可分类。通过允许更灵活的决策边界,GLVQ可以在许多分类任务上实现更高的精度。
总的来说,GLVQ提供了一种独特而强大的分类方法,其处理非线性可分离数据的能力使其成为可用的分类算法集的一个有价值的补充。