订阅本专栏,有大量的数学建模教程,从零基础到后续的实战案例,篇篇都有源码和讲解。
一、简介
支持向量机(SVM) 是一种有监督的机器学习分类算法。在二维线性可分数据的情况下,如图所示,典型的机器学习算法试图找到一个划分数据的边界,以使误分类误差最小化。如果您仔细查看下图,可能有几个边界可以正确划分数据点。两条虚线和一条实线对数据进行了正确分类。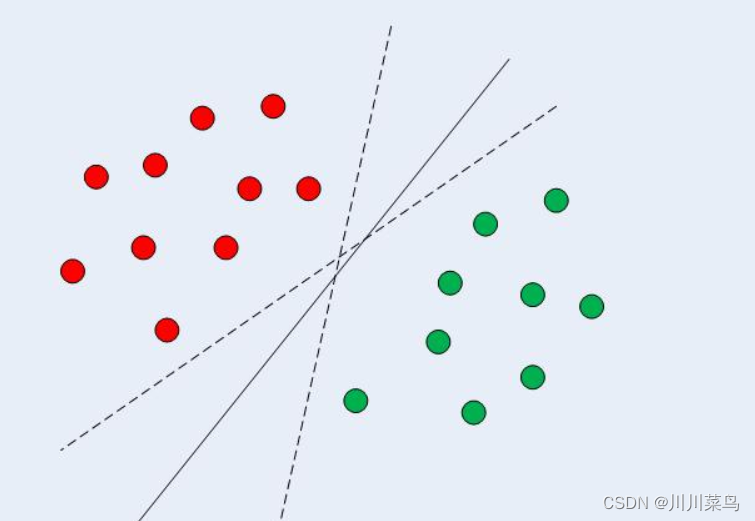
SVM 与其他分类算法的不同之处在于它选择的决策边界使与所有类的最近数据点的距离最大化。SVM 不只是找到一个决策边界。它找到了最优的决策边界。
最优决策边界是与所有类的最近点具有最大边距的决策边界。决策边界与点之间距离最大的离决策边界最近的点称为支持向量,如下图 所示。在支持向量机的情况下,决策边界称为最大边距分类器,或最大边距超平面.
二、使用 Scikit-Learn 实现 SVM
我们的任务是根据钞票的四个属性来预测钞票是否真实,即小波变换图像的偏度、图像的方差、图像的熵和图像的弯曲度。这是一个二分类问题,我们将使用 SVM 算法来解决这个问题。本节的其余部分包括标准的机器学习步骤。
数据如下: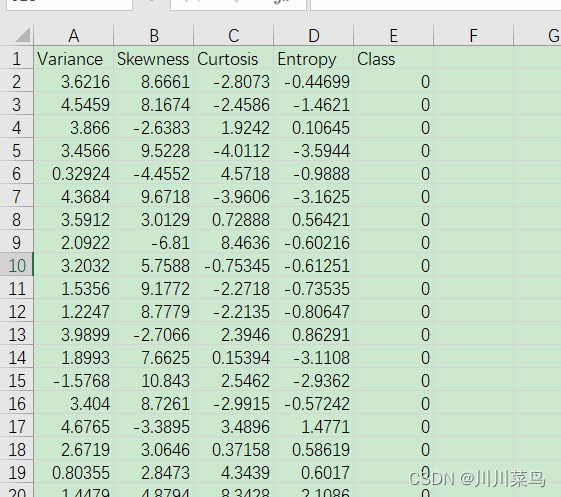
数据下载:
链接:https://pan.baidu.com/s/1WAVFi-zutaenVAfURL0_aw?pwd=kqrm
提取码:kqrm
数据是从取自真实和伪造的钞票样样本的图像中提取的。
数据的属性如下:
- 小波变换图像的方差(连续)
- 小波变换图像的偏度(连续)
- 小波变换图像的弯曲度(连续)
- 图像的熵(连续)
- 类(整数)
下面我们开始正式对该数据进行分类,使用SVM分类。
2.1 数据读取
import pandas aspd
bankdata = pd.read_csv("data.csv")
bankdata
如下: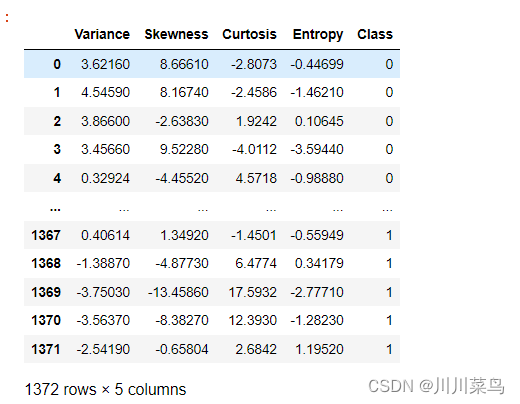
2.2 探索性数据分析
探索的很多,这里简单介绍一点。
查看维度:
bankdata.shape
输出为:(1372, 5),意味着该数据有1372行,5列。
查看数据描述:
bankdata.describe()
如下: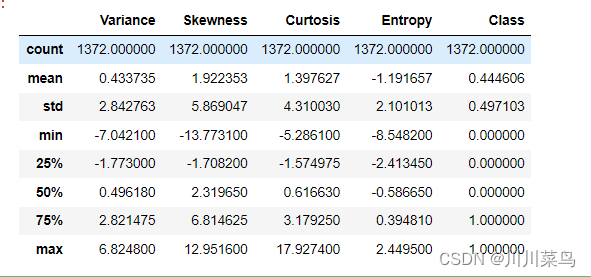
2.3 数据预处理
数据预处理包括
(1)将数据划分为属性和标签
(2)将数据划分为训练集和测试集。
要将数据划分为属性和标签,执行以下代码:
X = bankdata.drop('Class', axis=1)
y = bankdata['Class']
在上面脚本的第一行中,数据框的所有列bankdata都存储在X变量中,除了“Class”列,即标签列。drop()方法删除此列。在第二行中,只有Class列存储在y变量中。此时X变量包含属性,而y变量包含相应的标签。
一旦数据被划分为属性和标签,最后的预处理步骤就是将数据划分为训练集和测试集。幸运的是,model_selectionScikit-Learn 库的库包含train_test_split允许我们将数据无缝划分为训练集和测试集的方法,实现如下:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test =train_test_split(X, y, test_size =0.20)
2.4 训练算法
我们将数据分为训练集和测试集。现在是在训练数据上训练我们的 SVM 的时候了。Scikit-Learn 包含该svm库,其中包含用于不同 的SVM 算法的内置类。由于我们要执行分类任务,我们将使用支持向量分类器类,它是SVC在 Scikit-Learn 的svm库中编写的。此类接受一个参数,即内核类型。这个非常重要。在简单 SVM 的情况下,我们只需将此参数设置为“linear”,因为简单 SVM 只能对线性可分数据进行分类。我们将在下一篇中看到非线性内核。
fit调用 SVC 类的方法在训练数据上训练算法,将其作为参数传递给fit方法。执行以下代码来训练算法:
from sklearn.svm import SVC
svclassifier =SVC(kernel='linear')
svclassifier.fit(X_train, y_train)
输出如下:
2.5 做出预测
为了进行预测,使用predict了SVC类的方法。看看下面的代码:
y_pred = svclassifier.predict(X_test)
2.6 评估算法
混淆矩阵、精度、召回和 F1评分是分类任务最常用的指标。Scikit-Learn 的metrics库包含classification_report和confusion_matrix方法,可以很容易地用于找出这些重要指标的值。以下是查找这些指标的代码:
from sklearn.metrics import classification_report,confusion_matrixprint(confusion_matrix(y_test,y_pred))print(classification_report(y_test,y_pred))
输出如下: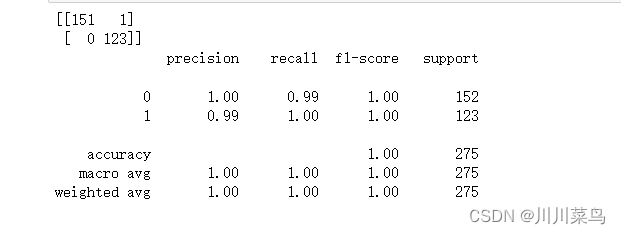
从结果可以看出,SVM 略优于决策树算法。与决策树算法的四个错误分类相比,SVM 算法只有一个错误分类。
precision :精确度
recall:召回率
f1-score: F1评分
三、内核支持向量机
在上一节中,我们看到了如何使用简单的 SVM 算法来找到线性可分数据的决策边界。然而,在非线性可分数据的情况下,例如下图 所示的数据,直线不能用作决策边界。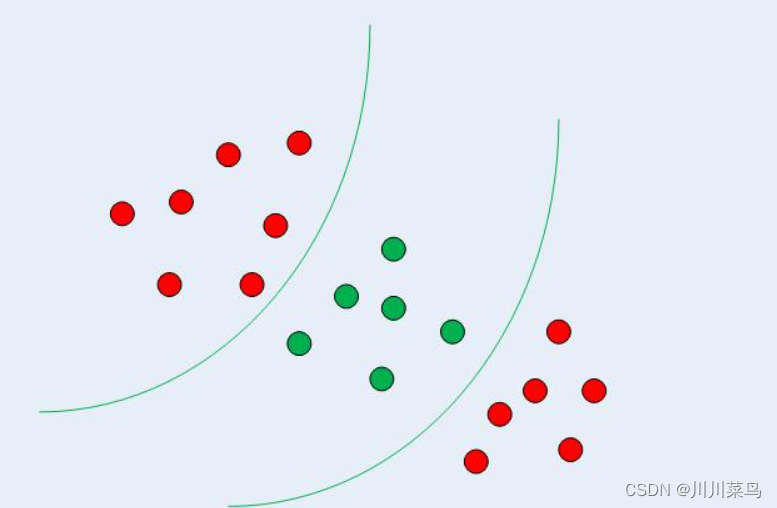
在非线性可分数据的情况下,不能使用简单的 SVM 算法。相反,使用了一个修改版本的 SVM,称为 Kernel SVM。
基本上,内核支持向量机将非线性可分数据的低维投影到高维的线性可分数据上,从而将属于不同类别的数据点分配到不同的维度。
3.1 使用 Scikit-Learn 实现内核 SVM
在本节中,我们将使用著名的iris 数据集根据四个属性预测植物所属的类别:萼片宽度、萼片长度、花瓣宽度和花瓣长度。
数据下载:
链接:https://pan.baidu.com/s/1J4dtmBr8_8ahSJqTrIceHg?pwd=g232
提取码:g232
32 导入库
import numpy asnp
import matplotlib.pyplot asplt
import pandas aspd
3.3 读取数据
colnames =['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']
irisdata = pd.read_csv('iris.data', names=colnames)
irisdata
读取如下: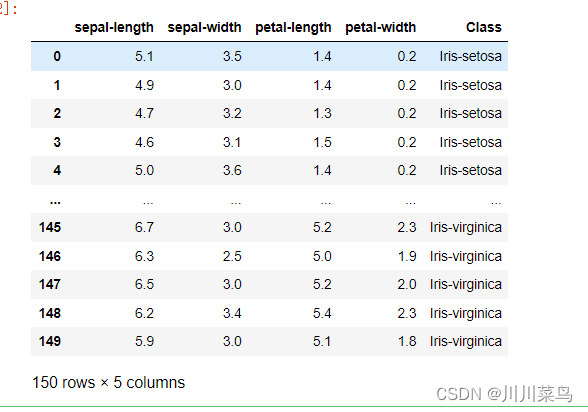
3.4 预处理
X = irisdata.drop('Class', axis=1)
y = irisdata['Class']
3.5 训练测试拆分
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test =train_test_split(X, y, test_size =0.20)
3.6 训练算法
对于内核 SVM,可以使用高斯、多项式、sigmoid 或可计算内核。我们将实现多项式、高斯和 sigmoid 内核,看看哪个更适合我们的问题。
(1) 多项式核
在多项式内核degree的情况下,您还必须为类的参数传递一个值SVC。这基本上是多项式的次数。看看我们如何使用多项式内核来实现内核 SVM:
from sklearn.svm import SVC
svclassifier =SVC(kernel='poly', degree=8)
svclassifier.fit(X_train, y_train)
如下:
做出预测
y_pred = svclassifier.predict(X_test)
评估算法
任何机器学习算法的最后一步都是评估:
from sklearn.metrics import classification_report,confusion_matrixprint(confusion_matrix(y_test, y_pred))print(classification_report(y_test, y_pred))
如下: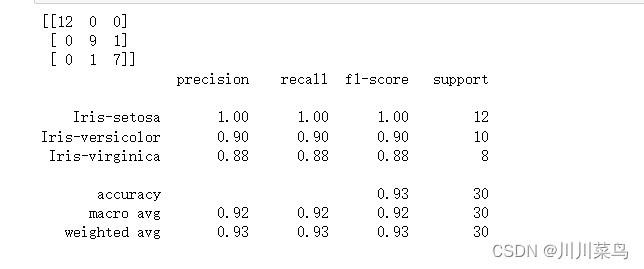
现在让我们对高斯和 sigmoid 内核重复相同的步骤。
(2)高斯核
from sklearn.svm import SVC
svclassifier =SVC(kernel='rbf')
svclassifier.fit(X_train, y_train)
y_pred = svclassifier.predict(X_test)
如下: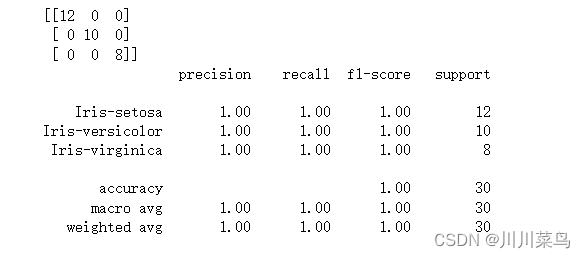
(3)Sigmoid 内核
from sklearn.svm import SVC
from sklearn.svm import SVC
svclassifier =SVC(kernel='sigmoid')
svclassifier.fit(X_train, y_train)
y_pred = svclassifier.predict(X_test)from sklearn.metrics import classification_report,confusion_matrixprint(confusion_matrix(y_test, y_pred))print(classification_report(y_test, y_pred))
带有 Sigmoid 内核的 Kernel SVM 的输出如下所示: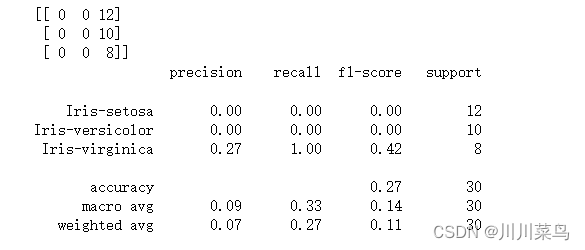
3.7 内核比较
如果我们比较不同类型内核的性能,我们可以清楚地看到 sigmoid 内核的性能最差。这是由于 sigmoid 函数返回两个值 0 和 1 的原因,因此它更适合二分类问题。然而,在我们的例子中,我们有三个输出类。
在高斯核和多项式核中,我们可以看到高斯核实现了完美的 100% 预测率,而多项式核错误分类了一个实例。因此,高斯核的性能稍好一些。但是,对于在每种情况下哪个内核性能最好,并没有硬性规定。这一切都是关于测试所有内核并选择在您的测试数据集上具有最佳结果的内核。
四、总结
根据实际情况选择一个最佳内核。有时间我会继续更新比较复杂的案例。
版权归原作者 川川菜鸟 所有, 如有侵权,请联系我们删除。