本文已收录于专栏
🌳《画解数据结构》🌳
文章目录
前言
好久没有写图论相关的文章了,趁着今天月黑风高,夜深人静,今天介绍一个利用贪心思想求解的算法,即图论中非常重要的概念,它就是:
「 最小生成树 」
一、概念
1、生成树
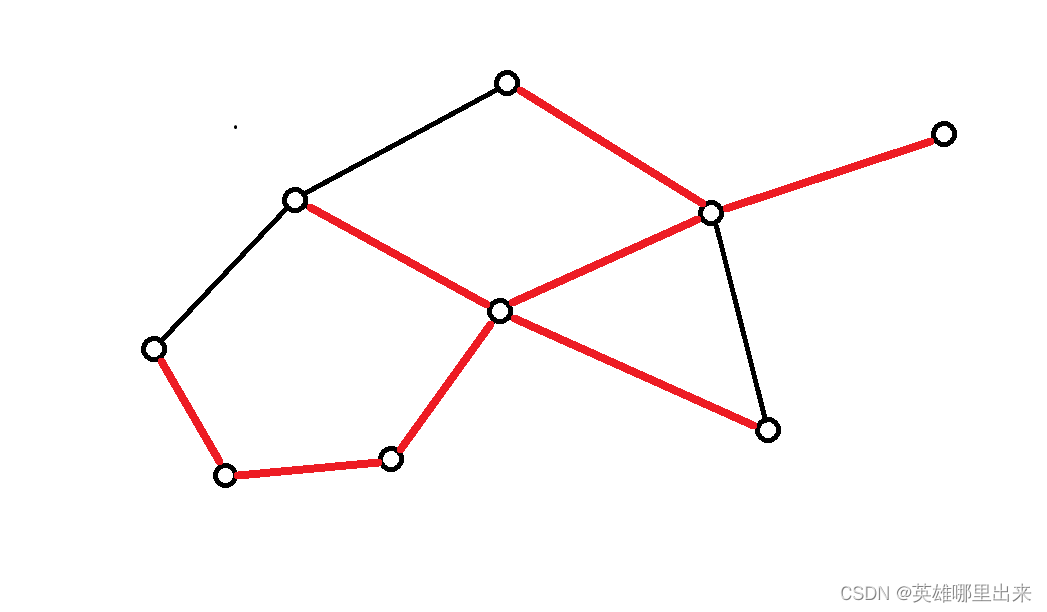
一个连通图,它的 极小连通子图 就是生成树。它含有图中所有的
n
n
n 个结点,并且只有能够构成树的
n
−
1
n-1
n−1 条边。如图所示的红色边就是其中一个生成树。
2、最小生成树
当图上的边有权值时,我们把构造这个 极小连通子图 的最小总代价生成树称为 最小生成树。如下图所示的红色线段组成的生成树就是最小生成树。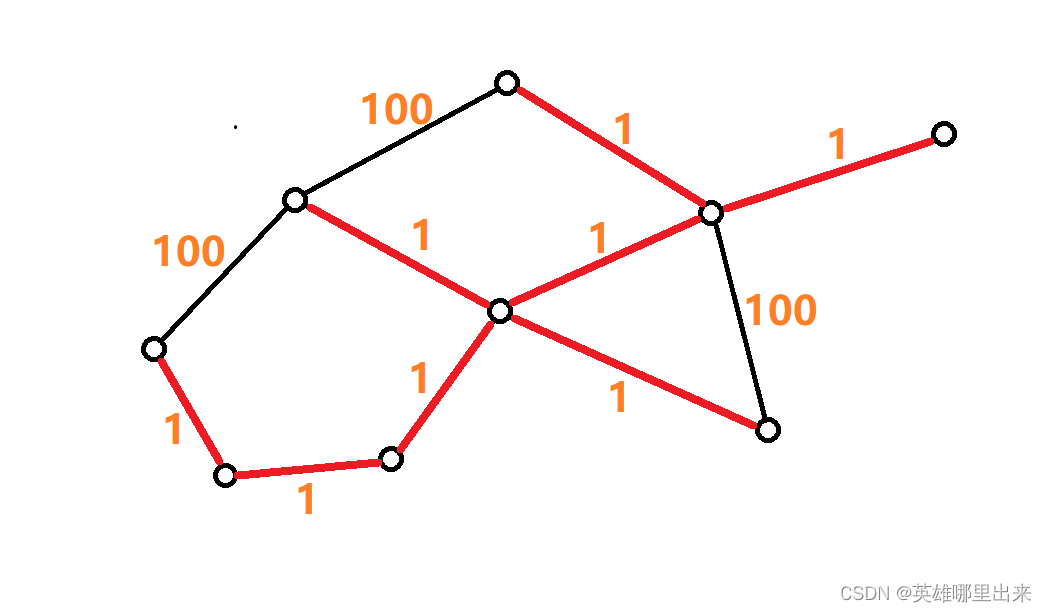
二、算法
找最小生成树的常用算法主要有三种:Prim、Kruscal、Boruvka。
1、Prim
1)算法描述
Prim 算法是基于贪心的,算法描述如下:
a. 利用邻接矩阵存储dist[i][j]两点
i i i 和 j j j 之间的距离;b. 用
cost[i]来表示 最小生成树集合 和 非最小生成树 中的点
i i i 的最小距离,当cost[i] = 0代表
i i i 就是 **最小生成树** 集合中的顶点。c. 由于是生成树,所以顶点
0 0 0 一定在树上,初始化cost[i]就是
0 0 0 和 i i i 的距离(因为 **最小生成树集合** 目前只有0)。d. 从
cost[i]中寻找一个值不为零(因为值为零表示是最小生成树集合中的点)且最小的顶点
u,那么
cost[u]一定是 最小生成树上的边。于是,
u也成了 最小生成树上的点。
e. 然后,继续用u去更新
cost[i],即更新 最小生成树集合 和 非最小生成树的点 之间的距离,回到 d 继续迭代计算。
2)源码剖析
intminSpanningTree(int n,int dist[maxn][maxn]){int i, u, ret, dis;int cost[maxn];for(i =0; i < n;++i){
cost[i]=(i ==0)?0: dist[0][i];// (1) }
ret =0;// (2)while(1){
dis = inf;for(i =0; i < n;++i){// (3)if(cost[i]&&lessthan(cost[i], dis)){
dis = cost[i];
u = i;}}if(dis == inf){return ret;// (4)}
ret += cost[u];// (5)
cost[u]=0;// (6)for(i =0; i < n;++i){// (7)if(cost[i]&&lessthan(dist[u][i], cost[i])){
cost[i]= dist[u][i];}}}return inf;}
( 1 ) (1) (1)```cost[i]```表示 **当前最小生成树集合** 和 **当前非最小生成树** 中的点 i i i 的最小距离,当```cost[i] = 0```代表 i i i 就是 **当前最小生成树** 集合中的顶点;( 2 ) (2) (2)```ret```用来存储最小生成树边权之和,初始化为 0;( 3 ) (3) (3) 从```cost[i]```中寻找一个值不为零(因为值为零表示是最小生成树集合中的点)且最小的顶点```u```,那么 ```cost[u]```一定是 **最小生成树上的边**。于是,```u```也成了 **最小生成树上的点**;( 4 ) (4) (4) 整个查找过程完成,直接返回最小生成树的边权总和;( 5 ) (5) (5) 将当前边```cost[u]```加入最小生成树;( 6 ) (6) (6) 将当前点```u```加入最小生成树;( 7 ) (7) (7) 继续用```u```去更新```cost[i]```,即更新 **最小生成树集合** 和 **非最小生成树的点** 之间的距离;
3)动图详解

4)时间复杂度
当有
n
n
n 个结点的时候,每个结点第一次被加入 **最小生成树集合** 的时候,都要更新其它结点的距离,一共
n
n
n 个结点,所以时间复杂度为
O
(
n
2
)
O(n^2)
O(n2)。
2、Kruscal
前置算法:夜深人静写算法(五)- 并查集
1)算法描述
Kruscal 算法也是基于贪心,并且采用 并查集 实现,算法描述如下:
a. 将图中所有的边按照三元组( u , v , w ) (u, v, w) (u,v,w) 来存储。b. 然后按照第三关键字
w w w 将所有边进行递增排序;c. 顺序取边,并且判断当前边
( u , v ) (u, v) (u,v) 的两个顶点 u u u 和 v v v 是否在同一个集合。如果不在,则这条边就是 **最小生成树** 上的边,权值累加,合并两个点;如果在,则这条边舍去;d. 反复迭代取边,直到总共取了
n − 1 n-1 n−1 条边,则算法结束。
2)源码剖析
#definemaxn1010int pre[maxn];voidunionfind_init(int n){// (1)for(int i =0; i < n;++i){
pre[i]= i;}}intunionfind_find(int x){// (2)return pre[x]== x ?(x):(pre[x]=unionfind_find(pre[x]));}
bool unionfind_union(int x,int y){// (3)int px =unionfind_find(x);int py =unionfind_find(y);if(px == py){return false;}
pre[px]= py;return true;}structKEdge{// (4)int u, v, w;}E[maxn * maxn];intcmp(constvoid* a,constvoid* b){// (5)structKEdge*pa =(structKEdge*)a;structKEdge*pb =(structKEdge*)b;return pa->w - pb->w;}// 点的个数 n,边的个数 mintKruscal(int n,int m,structKEdge* edges){int i, ret =0;int edgeCnt =0;qsort(edges, m,sizeof(structKEdge), cmp);// (6)unionfind_init(n);// (7)for(i =0; i < m;++i){if(unionfind_union( edges[i].u, edges[i].v )){
ret += edges[i].w;// (8)if(++edgeCnt == n-1){// (9)return ret;}}}return0;}
( 1 ) (1) (1) 并查集的初始化;( 2 ) (2) (2) 带路径压缩的并查集查找操作;( 3 ) (3) (3) 并查集的合并操作;( 4 ) (4) (4) 定义边三元组;( 5 ) (5) (5) 按照边权从小到大排序的回调函数;( 6 ) (6) (6) 对所有边进行排序;( 7 ) (7) (7) 初始化所有结点的并查集信息;( 8 ) (8) (8) 将当前边加入到最小生成树中;( 9 ) (9) (9) 如果边数等于 n − 1 n-1 n−1 则找到解,直接返回;
3)动图详解

4)时间复杂度
由于对边进行了一次排序,所以当边数为
m
m
m 时,时间复杂度为
O
(
m
l
o
g
m
)
O(mlog_m)
O(mlogm)。
3、Boruvka
前置算法:夜深人静写算法(七)- 字典树
1)算法描述
Boruvka 解决的问题较为特殊,求的是异或的最小生成树。具体问题为:给定
n ( n ≤ 200000 ) n (n \le 200000) n(n≤200000) 个点完全图,给定点权值 a i ( a i ≤ 2 30 ) a_i(a_i \le 2^{30}) ai(ai≤230),每条边的权值为边的两点的异或值,原题见:codeforces/contest888/G。
这个算法实现采用的是字典树。
a. 将所有数按照递增排序;
b. 将所有排好序的数字,按照顺序,从高位到低位,插入到高度固定的 01-字典树 中;
c. 分治求解,对于一棵子树,如果只有左子树,那么最小生成树就一定在左子树上;如果只有右子树,那么最小生成树一定在右子树上;否则就应该是 左子树 的情况 + 右子树的情况,再加上左子树中选出一个点,右子树中选出一个点,连边,并且取最小值。
2)源码剖析
2.1)数据结构
#include<iostream>#include<cstring>#include<string>#include<algorithm>#include<cstdlib>#include<cstdio>usingnamespace std;#definemaxn200010#definemaxb31#definemaxnodes(maxn*maxb)#defineUNDEF-1#defineROOT0structTrieNode{int nodes[2];// (1)int l, r;// (2)}T[maxnodes];int TrieNodes;// (3)int a[200010];voidInit(){// (4)memset(T, UNDEF,sizeof(T));
TrieNodes =1;}intGetTrieNode(){// (5)return TrieNodes++;}
( 1 ) (1) (1) 字典树结点的两个子结点(0 和 1);( 2 ) (2) (2) [ l , r ] [l, r] [l,r] 代表以当前结点为根的子树,管辖的 原数组 a [ ] a[ ] a[] 的区间范围;( 3 ) (3) (3)```TrieNodes```本次样例计算中,字典树结点的总个数;( 4 ) (4) (4) 对字典树结点进行初始化;( 5 ) (5) (5) 生成一个新的字典树结点;
2.2)插入
首先,把所有的数字先映射到一棵 01 字典树 上。如图所示,代表的是一个至多三位的集合组成的字典树。其中集合中的元素可重复,分别为
{
(
001
)
2
,
(
011
)
2
,
(
011
)
2
,
(
100
)
2
}
\{ (001)_2, (011)_2, (011)_2, (100)_2\}
{(001)2,(011)2,(011)2,(100)2}。

绿色 代表字典树边权;
红色 代表集合中的十进制数转换成二进制以后,映射到字典树的情况;
蓝色 代表字典树根结点到当前结点的边路径组成的二进制序列;
橙色 代表这个数字在集合中出现的次数。
voidTrieInsert(int x,int idx){// (1)int now = ROOT;// (2)for(int i = maxb-1; i >=0;--i){int bit =((x>>i)&1);// (3)if(T[now].nodes[bit]== UNDEF){// (4)
T[now].nodes[bit]=GetTrieNode();}if( T[now].l == UNDEF ){// (5)
T[now].l = idx;}
T[now].r = idx;// (6)
now = T[now].nodes[bit];// (7)}}
( 1 ) (1) (1)```void TrieInsert(int x, int idx)```代表将 ```x = a[idx]```按照从高到低位插入到字典树中,```idx```代表排序后数组```a```的下标;( 2 ) (2) (2) 从根结点开始;( 3 ) (3) (3) 计算 x x x 的第 i i i 位,存储到```bit```中;( 4 ) (4) (4) 如果对应子树不存在,则创建一个新的字典树结点;( 5 ) (5) (5) 如果对应原数组左区间不存在,则置为当前下标;( 6 ) (6) (6) 枚举到当前下标,则右区间一定是当前下标;( 7 ) (7) (7) 迭代枚举子树;
2.3)查询
查询就是给定 一棵子树 和 一个值
x
x
x,要求在 **给定子树** 上找到和
x
x
x 异或最小的值;
longlongTrieQuery(int now,int depth,int x){longlong ret =0;for(int i = depth; i >=0;--i){// (1)int bit =((x>>i)&1);if(T[now].nodes[bit]!= UNDEF){// (2)
now = T[now].nodes[bit];}else{
now = T[now].nodes[bit^1];// (3)
ret +=(1<<i);}}return ret;// (4)}
( 1 ) (1) (1) 从当前深度往下迭代;( 2 ) (2) (2) 如果有和 x x x 一样的位,则尽量取一样,这样第 i i i 位异或得到的值为 0,一定更优;( 3 ) (3) (3) 反之,只能走另一棵子树,异或的值为 ```1<<i```,累加到结果中;( 4 ) (4) (4) 最后,返回所有的累加和;
2.4)分治
分治是在字典树上求解。
原理就是左子树看成是一个连通块,右子树看成是一个连通块,那么只需要枚举左子树中的任意点,并且在右子树中找到最小的异或值,这样就能把左右子树进行连通,形成生成树。
longlongBoruvka(int now,int depth){if(now == UNDEF){return0;// (1)}longlong l =Boruvka(T[now].nodes[0], depth-1);// (2)longlong r =Boruvka(T[now].nodes[1], depth-1);// (3)longlong ans = l + r;if(T[now].nodes[0]!= UNDEF && T[now].nodes[1]!= UNDEF){int x = T[now].nodes[0], y = T[now].nodes[1];// (4)longlong ret =1e9; ret *= ret;for(int i = T[x].l; i <= T[x].r;++i){// (5)
ret =min(ret,TrieQuery(y, depth-1, a[i])+(1<<depth));}
ans += ret;// (6)}return ans;}
( 1 ) (1) (1) 如果点集是空集,则最小生成树的值一定是 0,直接返回;( 2 ) (2) (2) 求左边集合(左子树)构成的连通图的最小生成树;( 3 ) (3) (3) 求右边集合(右子树)构成的连通图的最小生成树;( 4 ) (4) (4) 对于左子树```x```和右子树```y```;( 5 ) (5) (5) 枚举左子树中所有的元素,并且快速去右子树中查找和它异或的最小值,从而将左右子树变成连通的。由于在 d e p t h depth depth 深度进行的分叉,所以这里异或一定多了一部分 2 d e p t h 2^{depth} 2depth 出来,需要累加上去。( 6 ) (6) (6) 任何一个集合的最小生成树,就是左边连通图的最小生成树,和右边连通图的最小生成树,加上两个集合中最小的那条边,就是答案了。
3)时间复杂度
( 1 ) (1) (1) 插入:总共 n n n 个数,每个数插入都是 31 31 31 次,所以时间复杂度为 O ( n c ) O(nc) O(nc),其中 c = 31 c = 31 c=31;( 2 ) (2) (2) 查找:由于采用的是分治,每个结点都会遍历一次,每次遍历到非叶子结点,都需要去对方的集合中进行 31 次查找,均摊下来也是 O ( n c ) O(nc) O(nc)。
有关 🌳 最小生成树 🌳 的的内容到这里就完全结束了,如果还有什么疑问,可以添加作者微信咨询。
有关🌳《画解数据结构》🌳 的源码均开源,链接如下:《画解数据结构》
👇🏻添加 博主 获取付费专栏优惠券👇🏻
版权归原作者 英雄哪里出来 所有, 如有侵权,请联系我们删除。