神经网络架构和训练、自学习、棋盘对称性、Playout Cap Randomization,结果可视化
从我们之前的文章中,介绍了蒙特卡洛树搜索 (MCTS) 的工作原理以及如何使用它来获得给定棋盘状态的输出策略。我们也理解神经网络在 MCTS 中的两个主要作用;通过神经网络的策略输出来指导探索,并使用其价值输出代替传统的蒙特卡洛rollout算法。
在这一部分中,我们将从这个神经网络的架构开始,检查它的不同层、输入和输出。然后了解如何使用自我对弈训练网络和研究用于训练神经网络的损失函数。本文还将仔细研究训练的细节,包括特定于 Chain Reaction 游戏的数据增强技术和称为 Playout Cap Randomization 的方法提高训练效率。最后我们将可视化查看我们的工作成果。
神经网络架构
神经网络模型的输入形状为MxNx7,其中M和N分别为Chain Reaction游戏的行数和列数。图形中的数字“7”表示有7个通道,每个通道以二进制数据的形式存储的某些特定信息,如下面所示:
Description of the encoded state
Size of the state: M*N*7
channel 1 : stores the MxN map where red orbs are 1 in number
channel 2 : stores the MxN map where red orbs are 2 in number
channel 3 : stores the MxN map where red orbs are 3 in number
channel 4 : stores the MxN map where green orbs are 1 in number
channel 5 : stores the MxN map where green orbs are 2 in number
channel 6 : stores the MxN map where green orbs are 3 in number
channel 7 : MxN map of ones if it is red player's turn otherwise
a map of zeroes
下面的图片展示了神经网络的架构。
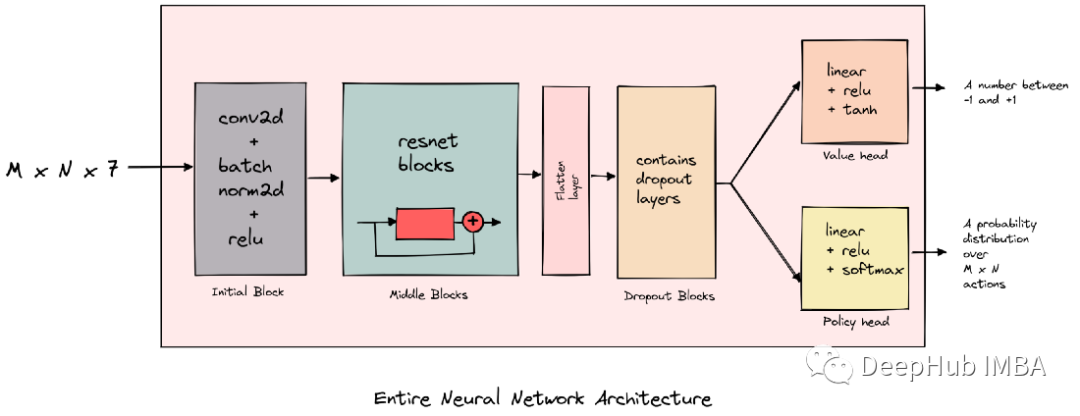
我们的神经网络结构是一个resnet结构-它有conv2d, batchnorm2d和relu层,dropout层和两个任务头。
输出值的头有一个tanh激活函数,产生一个介于-1和+1之间的数字。策略头有一个softmax函数,它帮助我们得到板子上所有动作的概率分布。
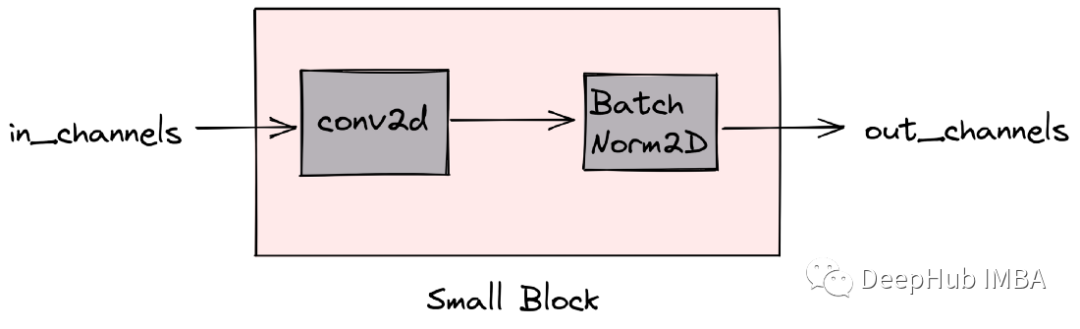
基本块(small block)如上图所示与resnet类似,我们会将这些基本块进行组合。
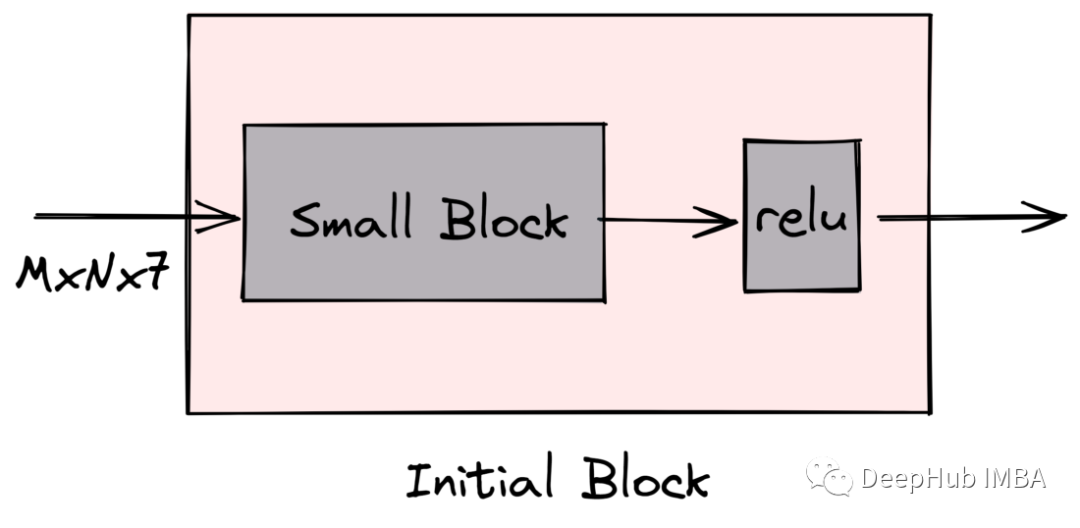
输入通过的第一个块由conv2d、batchnorm2d和relu层组成
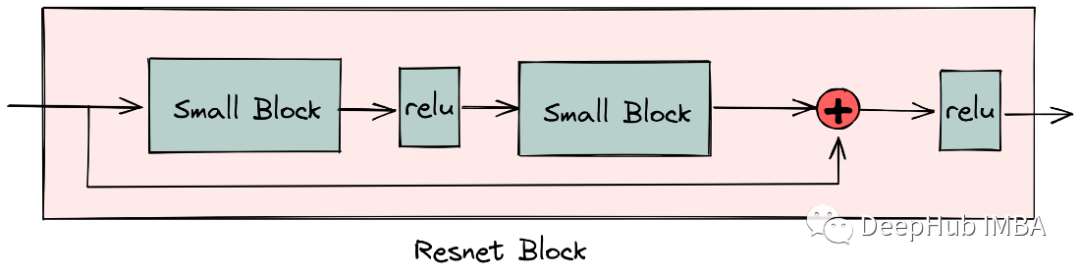
由基本块(conv2d和batchnorm2d层)和relu层组成我们上图所示的残差块(resnet)
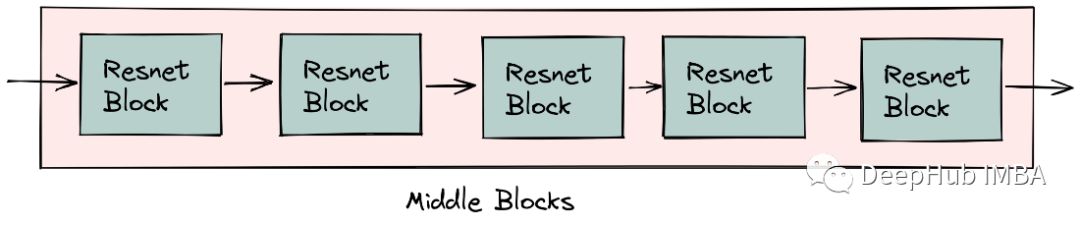
五个resnet块组成了我们神经网络的中间块
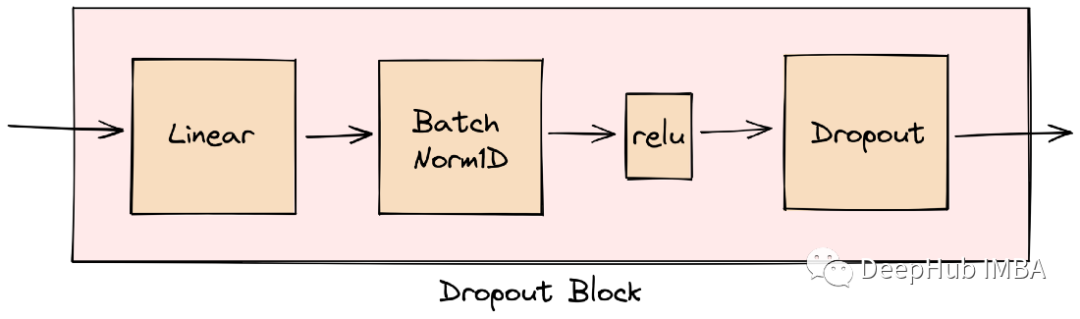
dropout块接收前一个块的输出,其中的linear层起到控制维度数的作用
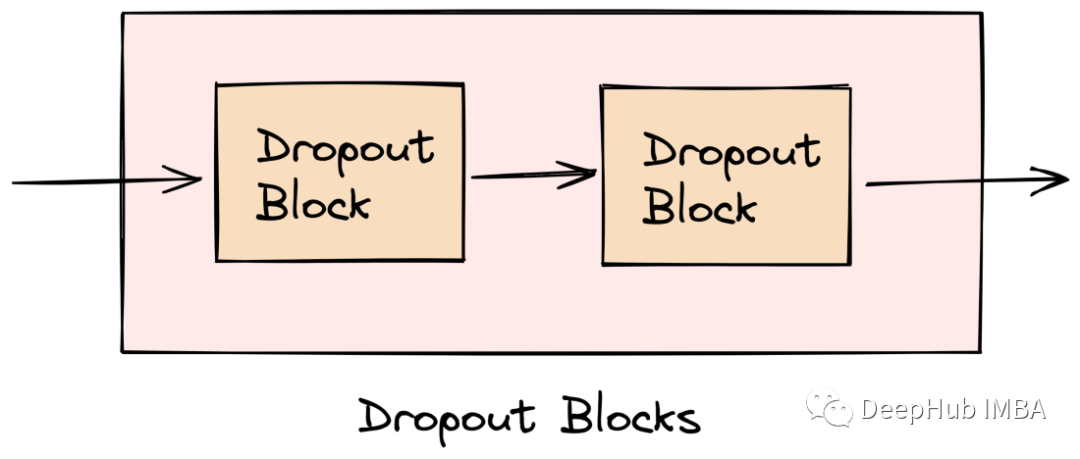
我们的网络结构中使用了两个dropout块
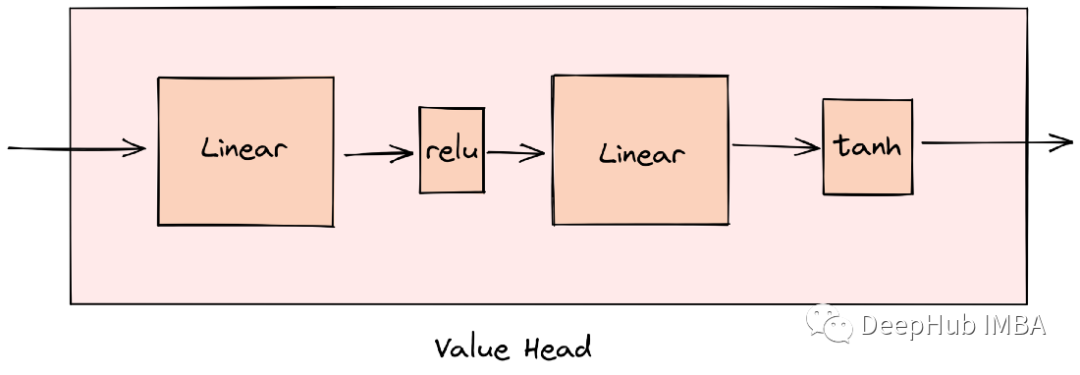
值头输出的是-1,1之间的动作价值(value)
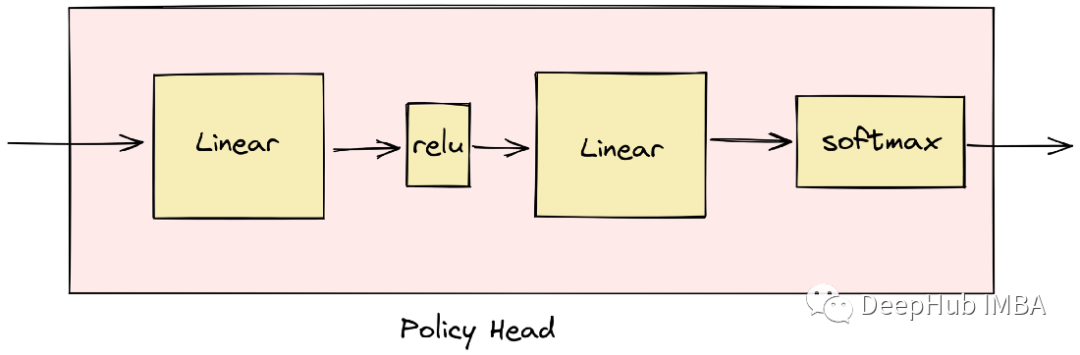
策略头输出被用作棋盘上所有动作的概率分布(0,1之间)
下图显示了使用PyTorch在Python中实现该体系结构的代码。
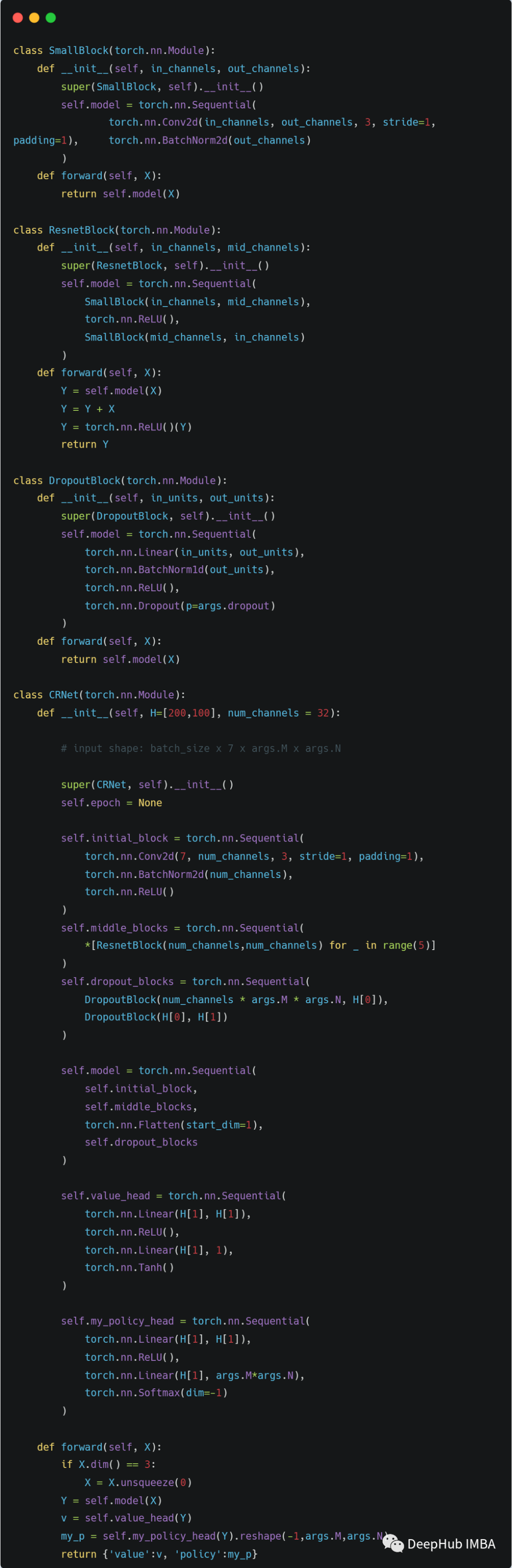
完成了我们模型架构,下面就要看下如何进行训练了
自我对局

上图显示了在游戏中如何进行任何单个操作的流程。在自我对局框架中,我们有两个玩家(都是AI),红色和绿色。每个玩家使用上述步骤进行操作。如果红色赢了游戏。对于所有的红色移动,目标值+1,对于所有的绿色移动,目标值是-1。
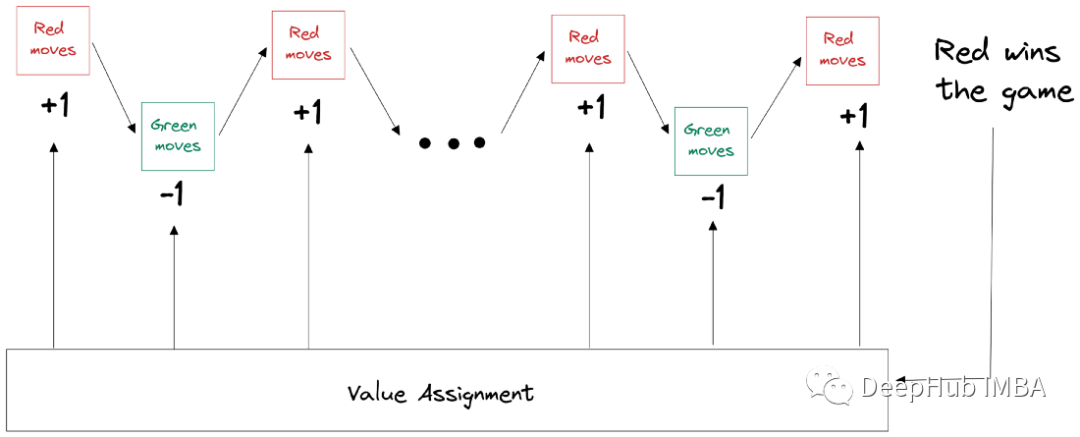
我们获得策略目标将是使用蒙特卡洛搜索树获得的策略。
损失函数
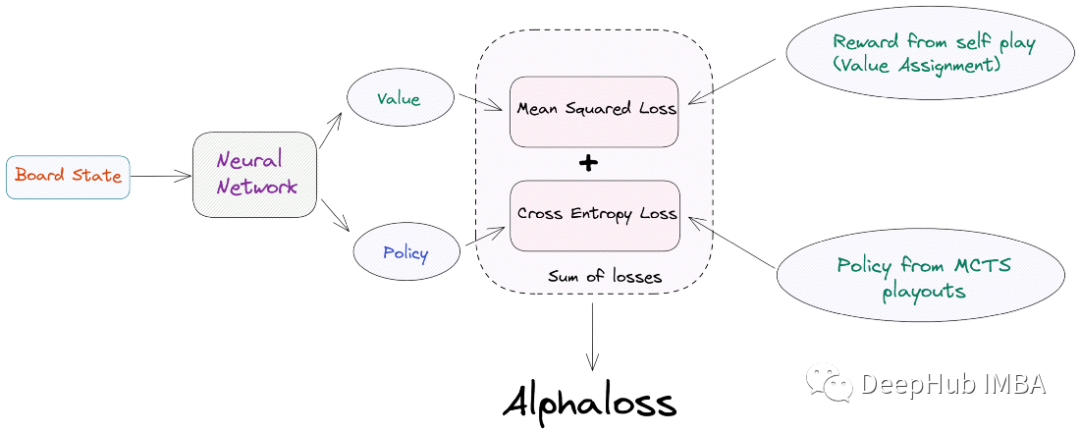
因为我们有2个任务头,所以损失函数需要包含自价值损失和策略损失
AlphaZero的损失函数如下:
- 价值损失:在游戏结束时使用价值分配获得的预测值和目标价值之间的均方损失。
- 策略损失:在预测的策略和从MCTS演习中获得的策略目标之间计算交叉熵损失。
在AlphaZero中训练神经网络的损失就是这两个损失的总和。我们称之为“AlphaLoss”。
数据增强
为了提高训练效率,我们可以这样操作:如果我们知道一个棋盘状态的正确策略,那么我们就知道通过旋转、翻转或转置棋盘矩阵获得的其他七个棋盘状态的正确策略,这就是我们所说的棋盘的对称性。
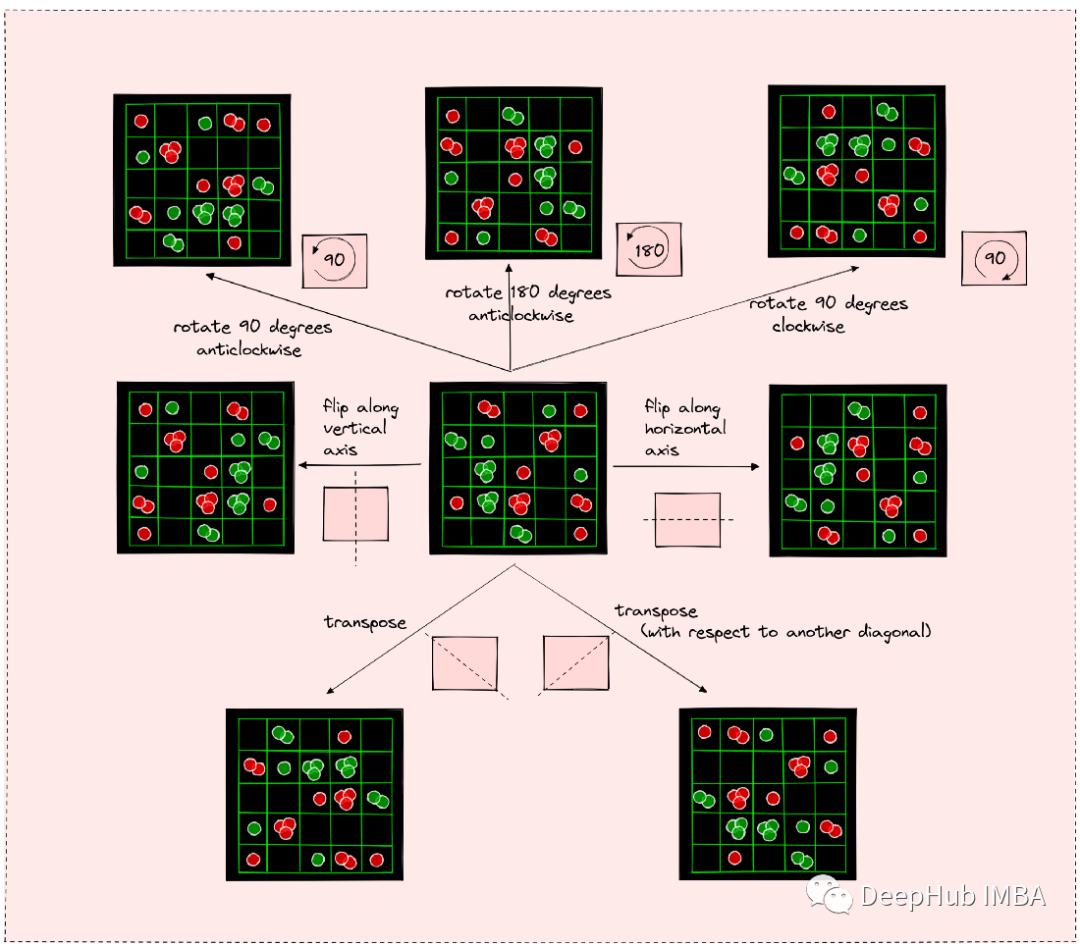
通过翻转、旋转和换位可以产生7种以上的棋盘状态。对于所有这些状态,我们可以很容易地获正确的政策。
为了在代码中实现这一点,我们需要一个其中存储了棋盘状态和策略目标的缓存区,在游戏结束获得实际奖励值时,目标值分配给临时缓冲区中的每个元素。
下图是构造这个缓存的代码
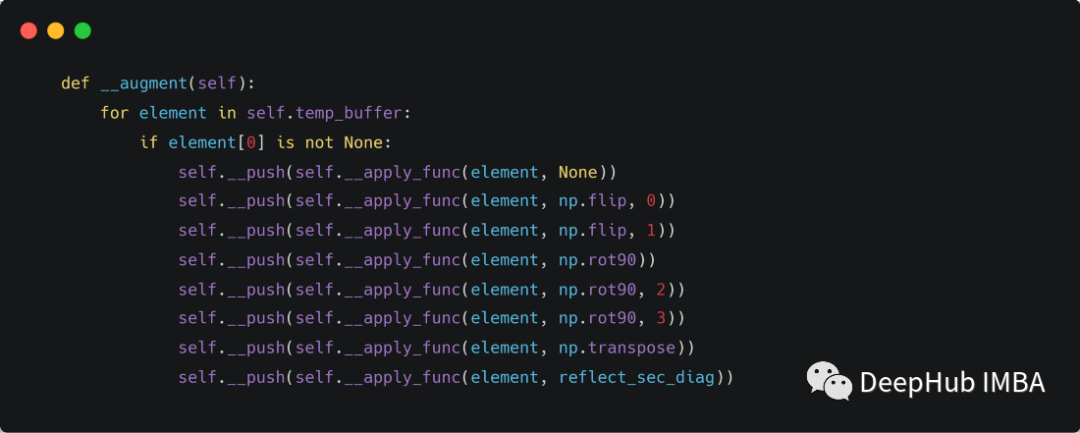
Playout Cap Randomization
我们还可以引入了Playout Cap Randomization,因为它有助于提高培训效率。
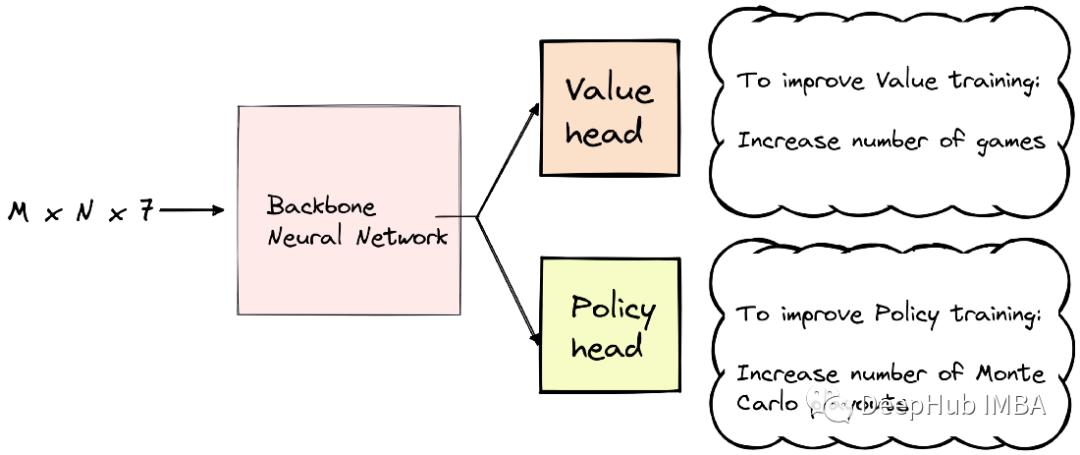
AlphaZero的自我游戏训练过程,它得到的唯一真正奖励是在游戏结束时,所以获得的奖励是非常少的,而价值头专注于预测这个奖励,如果我们想改善价值训练,就需要增加AlphaZero的游戏的次数。
如果我们想提高策略训练,我们则可以关注更多的蒙特卡洛回放。
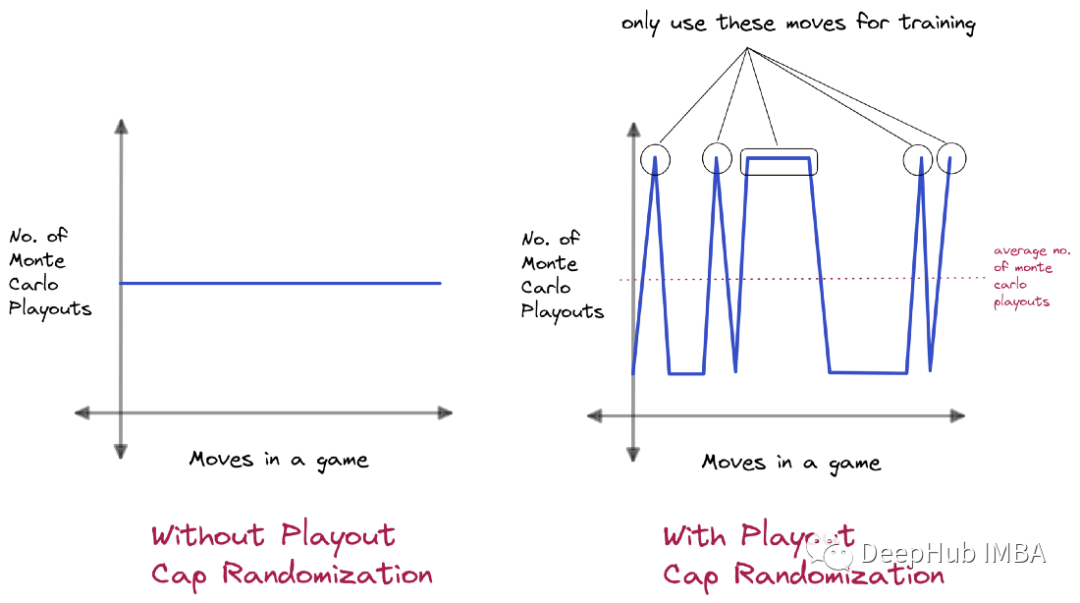
这里我们可以只增加一些随机选择的动作而不是增加游戏中所有动作的使用次数,只使用一些特定的动作的数据进行训练。在其他动作中,我们可以减少其选择次数。这种技术被称为Playout Cap Randomization。
结果展示
最后让我们看看我们的训练成果
对阵一个随机的代理
随机的代理没有任何策略,只是在棋盘上随机的进行可用的操作。以下是在3x3, 4x4和5x5棋盘上对随机代理的胜率。
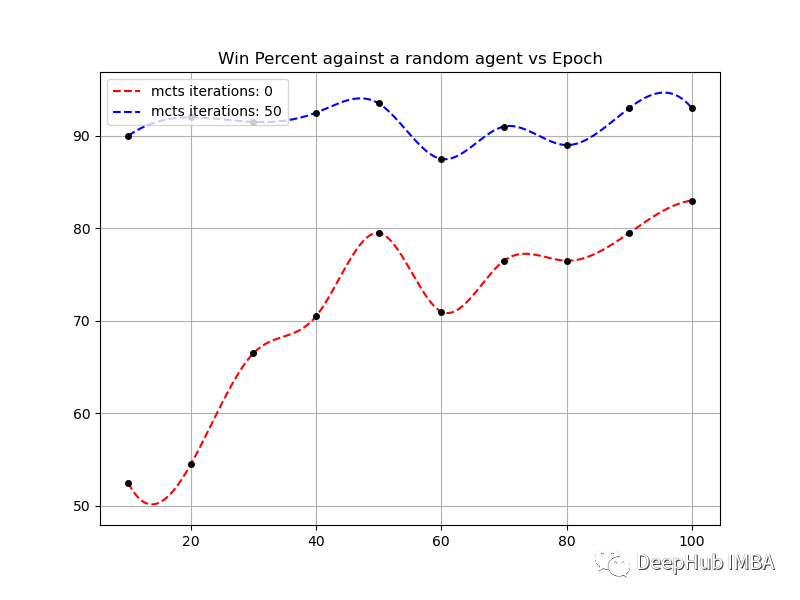
可以看到对于一个3 x 3的棋盘,即使没有MCTS,在80个回合后至少可以达到75%的胜率
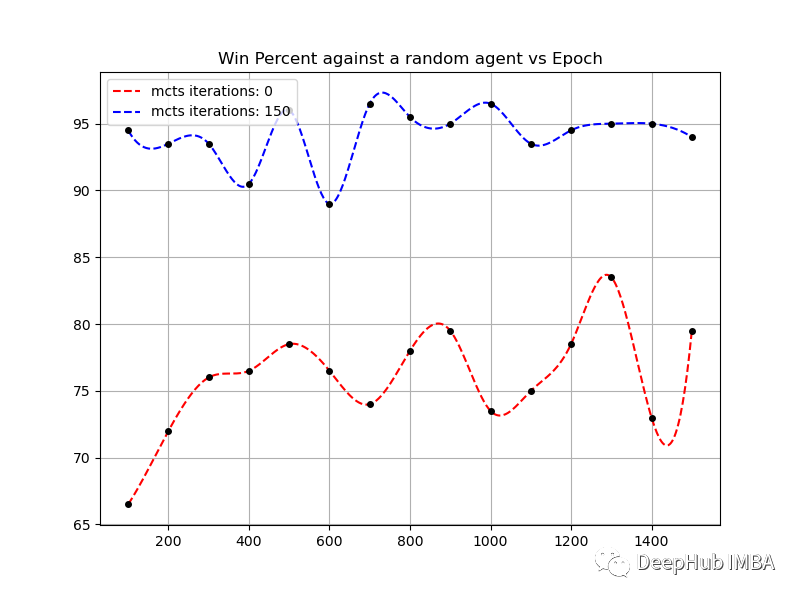
对于一个4 x 4的棋盘,训练在500个回合后就会饱和,然后就会变成振荡,但在1300回合附近,没有MCTS的代理的胜率超过80%
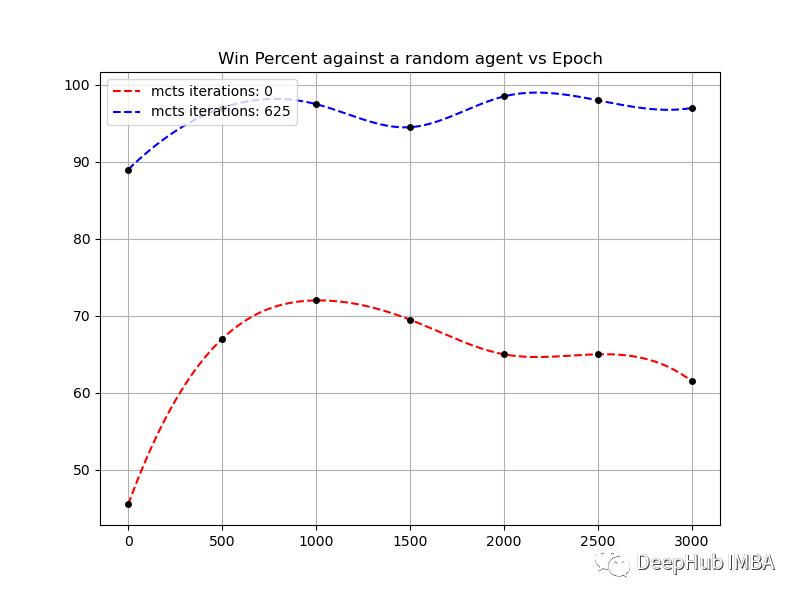
对于一块5 x 5的棋盘来说,训练在1000个周期左右就饱和了
可视化
每一场比赛都包括棋盘上的一系列动作。对于一块5x5的棋盘,第一步有25种可能。随着训练的进行,神经网络的值头输出不断提高,从而改进了蒙特卡罗搜索。以下是这些动作的可视化。可视化是针对一个5 x 5的棋盘,所以有25种可能性。这25种可能被映射到一个圆(在开始)或一个弧(后面经过训练)。

在1000次蒙特卡洛演练中使用未经训练的值网络所采取的行动。(5 × 5-> 25动作)。25个动作被映射到圆/圆弧中的角度。搜索最多只能到达4步的深度。
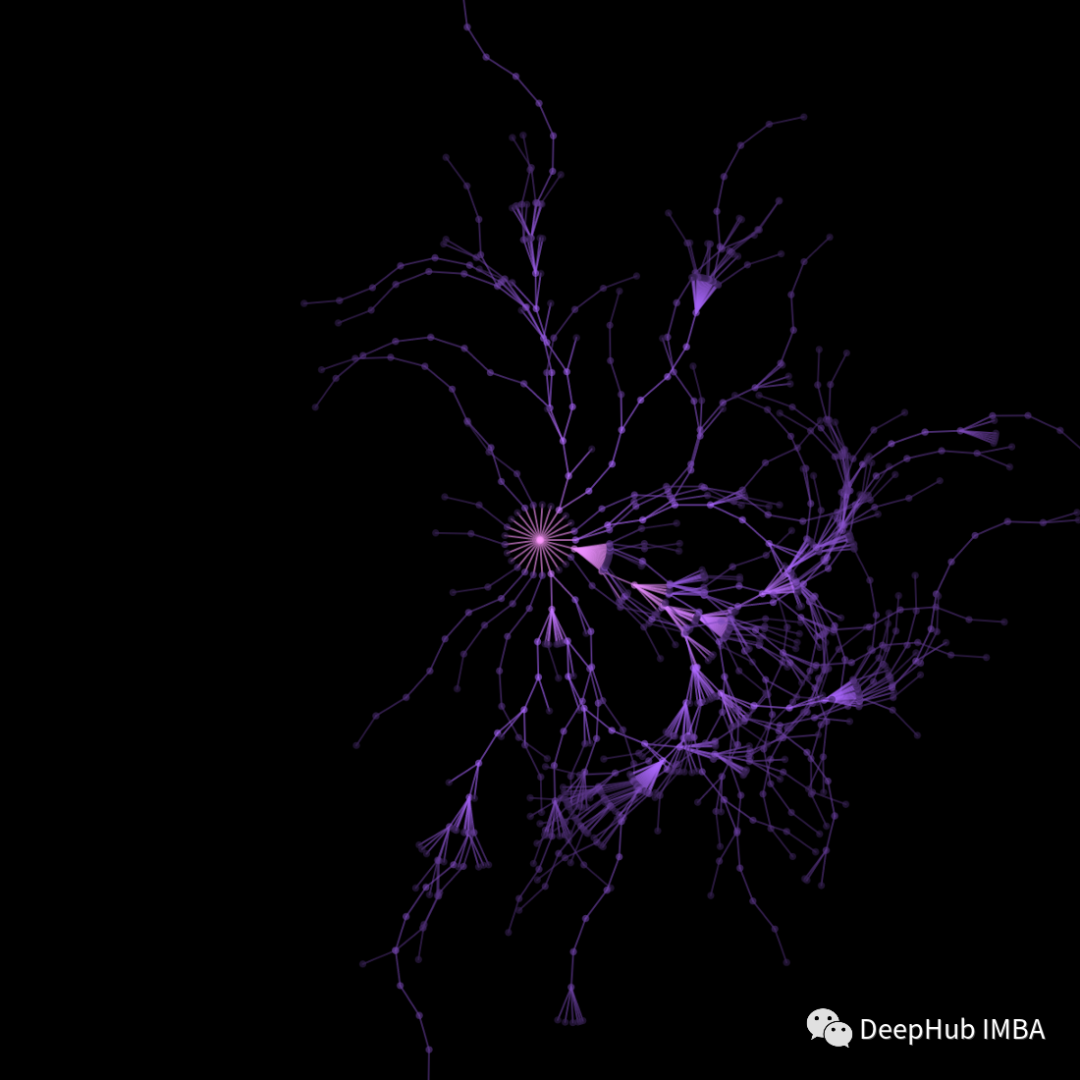
25个动作被映射到圆/圆弧中的角度。由于价值网络启发式的存在,搜索甚至深入到20步。
未来的发展方向
Chain Reaction的游戏有一个人类精心设计的启发式策略[2]。训练一个简单AlphaZero代理并试着让它与这样的策略竞争是很有趣的。
有一种称为hidden queen chess”/ “secret queen chess”的国际象棋变体,其中每个玩家在游戏开始时选择他们的一个棋子作为皇后,并且该选择不会向对手透露。但是 AlphaZero 适用于完美信息博弈和实施训练代理在信息不完善的状态下策论的论文会很有趣 [3]。
如果能够超越离散动作空间[4]将是有趣的。连续动作空间将在机器人或自动驾驶汽车应用中更为常见。[4]接受beta分布并学习它的参数。然后使用这个分布的一个缩放版本来近似有界连续空间。
我们有一个在3x3的Chain Reaction棋盘上训练一个效果非常好的代理。如果我们能将这些知识转移到4x4大小或其他大小的棋盘上,那就太好了。这项工作的重点也是一个方向[5]。如果没有这样的传输机制,在更大的棋盘上上进行训练在计算上是非常昂贵的,例如:15x15或20x20棋盘。
本文代码:https://github.com/BentouAI/AlphaZero-Chain-Reaction
引用参考
- Wu, D.J. (2020) Accelerating self-play learning in go, arXiv.org. Available at: https://arxiv.org/abs/1902.10565v5.
- Chain Reaction (Game). Brilliant.org. Retrieved 17:59, November 27, 2022, from https://brilliant.org/wiki/chain-reaction-game/
- https://www.deepmind.com/blog/alphastar-grandmaster-level-in-starcraft-ii-using-multi-agent-reinforcement-learning
- Moerland, T.M., Broekens, J., Plaat, A. and Jonker, C.M., 2018. A0c: Alpha zero in continuous action space. arXiv preprint arXiv:1805.09613.
- Ben-Assayag, S. and El-Yaniv, R., 2021. Train on small, play the large: Scaling up board games with alphazero and gnn. arXiv preprint arXiv:2107.08387.
作者:Bentou