粒子群算法(PSO)优化的BP神经网络预测

摘要：

BP神经网络是一种常见的多层前馈神经网络，本文通过粒子群算法(PSO)对BP神经网络的网络参数进行寻优，得到最优化的网络参数，并与未使用PSO的BP网络对同一测试样本进行预测，对比分析并突出PSO-BP的优越性。该方法常于各种数学建模，由于结合了两种算法，使得其效果更佳，相比单一的方法更加出彩。本文章代码可改性强，注释详细，替换输入与输出后即可满足不同的任务，实现自己想要的功能，适合新入门神经网络的同学学习。

1.BP模型神经网络模型：

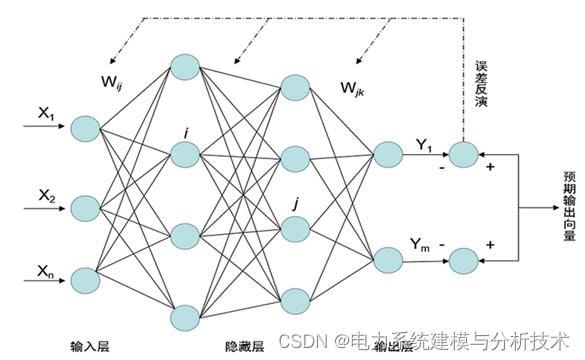
2.粒子群优化算法（PSO）：

粒子群算法的计算原理网上说的很多了，这里就不再继续介绍了，感兴趣的可以看看这位博主的文章：

大话算法 -- 粒子群算法_建模君Assistance的博客-CSDN博客_粒子群算法

3.粒子群算法结合BP神经网络（PSO-BP）：

BP神经网络的隐藏节点通常由重复的前向传递和反向传播的方式来决定，通过修改或构造训练方式改隐藏的节点数，相应的初始权重和阈值也会随之变化，从而影响网络的收敛和学习效率。 为了减少影响，通过采用基于粒子群算法的BP神经网络模型对权重和阈值的调整进行优化，从而加快网络的收敛速度和提高网络的学习效率。具体的计算流程如下：

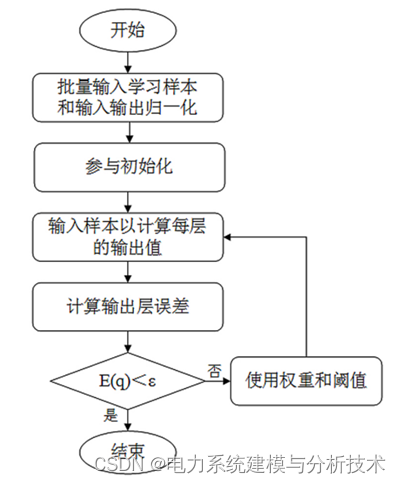
4.程序运行结果：

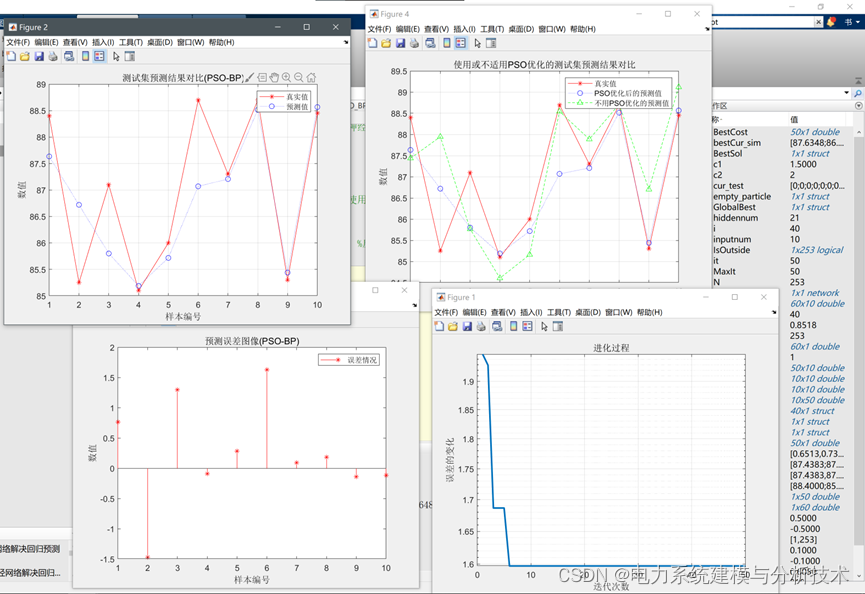
5.Matlab代码 ：

本文仅展示部分代码，需要全部代码请点击：🍞正在为您运送作品详情

%% 使用PSO优化BP神经网络解决回归预测问题
clc;
clear;
close all;
%% 导入数据
load data.mat; % 可以改成自己的数据
temp = randperm(size(NIR,1)); %打乱数据
%% 设置参数及输入P 输出T ，其中一行为一个样本，一列是一个特征
% 训练输入与输出
P = NIR(temp(1:50),:);
T = octane(temp(1:50),:);
% 测试输入与输出
P_test = NIR(temp(51:end),:);
T_test = octane(temp(51:end),:);
% BP神经网络参数定义
inputnum=size(P,2);                                     %输入层神经元个数
hiddennum=2*inputnum+1;                                 %初始隐层神经元个数
outputnum=size(T,2);                                    %输出层神经元个数
w1num=inputnum*hiddennum;                               %输入层到隐层的权值个数
w2num=outputnum*hiddennum;                              %隐层到输出层的权值个数
N=w1num+hiddennum+w2num+outputnum;                      %待优化的变量的个数
%% 定义粒子群优化算法参数
nVar=N;                                                 %变量数目
VarSize=[1,nVar];                                       %变量矩阵大小
VarMin=-0.5;                                            %变量取值下限
VarMax=0.5;                                             %变量取值上限
MaxIt=50;                                               %最大迭代次数
nPop=40;                                                %种群数目
w=1;                                                    %惯性权重
wdamp=0.99;                                             %惯性重量降低系数
c1=1.5;                                                 %个体学习系数
c2=2.0;                                                 %群体学习系数
VelMax=0.1*(VarMax-VarMin);                             %速度上限
VelMin=-VelMax;                                         %速度下限
%% 初始化
empty_particle.Position=[];
empty_particle.Cost=[];
empty_particle.Velocity=[];
empty_particle.Best.Position=[];
empty_particle.Best.Cost=[];
particle=repmat(empty_particle,nPop,1);
GlobalBest.Cost=inf;
for i=1:nPop
    %初始化位置
    particle(i).Position=unifrnd(VarMin,VarMax,VarSize);
    %初始化速度
    particle(i).Velocity=zeros(VarSize);
    %个体评价
    particle(i).Cost=BpFunction(particle(i).Position,P,T,hiddennum,P_test,T_test);
    %更新个体最优
    particle(i).Best.Position=particle(i).Position;
    particle(i).Best.Cost=particle(i).Cost;
    %更新群体最优
    if particle(i).Best.Cost<GlobalBest.Cost
        GlobalBest=particle(i).Best;
    end
end
BestCost=zeros(MaxIt,1);