（八）认证加密

认证加密（AE）

符号约定
符号含义*P明文K密钥C密文E()对称加密函数D()对称解密函数MAC()消息认证码函数T认证标签A*关联数据

认证加密（AE）算法既生成认证标签，也进行消息的加密。

加密计算方法：AE(K,P)=(C,T)

解密计算方法：AD(K,C,T)=P

认证加密的加密功能从根本上比普通密码算法更安全，因为只有在认证标签有效的情况下，持有密钥的系统才会对密文进行解密（在标签无效的情况下，将丢弃接收到的明文）。

使用MAC的认证加密

MAC和对称加密算法组合使用，有以下三种方式组合加密和认证：

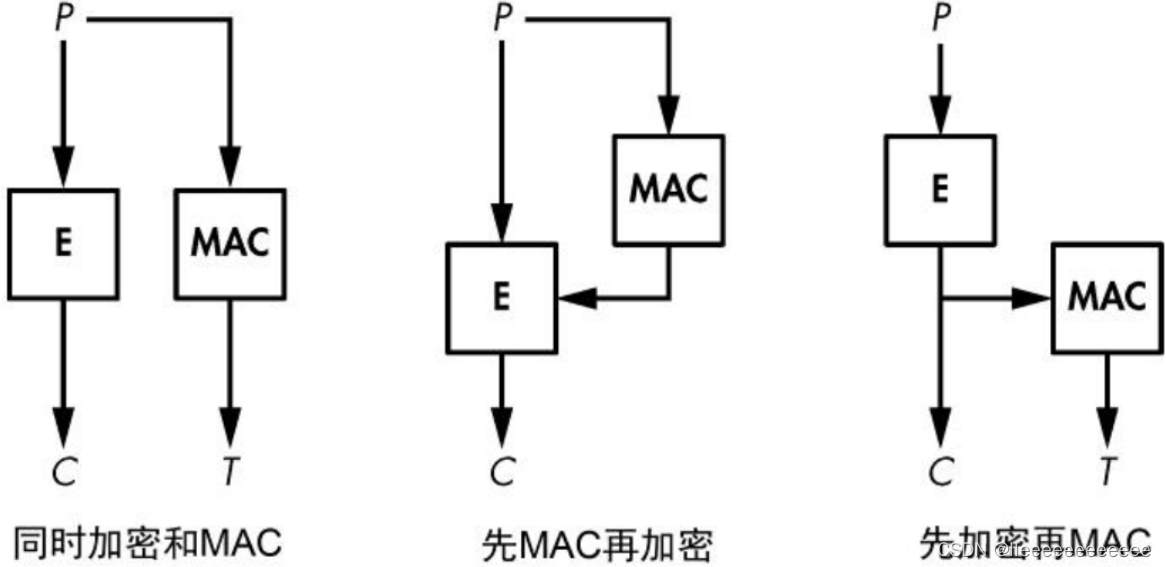
同时加密和MAC（三种之中最不安全）

发送者：

1.计算密文：C=E(K1,P)。

2.计算加密标签：T=MAC(K2,P)。

3.发送密文C和加密标签T。

上述步骤可同步进行。

接收者：

1.计算明文：P=D(K1,C)。

2.验证明文：T'=MAC(K2,P) ，比较T和T'是否相同。

先MAC再加密

发送者：

1.计算认证标签：T=MAC(K2,P)。

2.计算密文：C=E(K1,P || T)。

3.发送密文C。

接收者：

1.解密密文C：P || T=D(K1,C)，解出P和T。

2.计算标签：T'=MAC(K2,P)，比较T和T'。

先加密再MAC（三种之中最安全）

发送者：

1.计算密文：C=E(K1,P)。

2.计算认证标签：T=MAC(K2,C)。

3.发送密文C和标签T。

接收者：

1.计算认证标签：T'=MAC(K2,C)，比较T和T'，相等则执行2步骤。

2.计算明文：P=D(K1,C)。

使用关联数据的认证加密（AEAD）

关联数据：经认证加密处理的任何需要身份验证但不加密的数据。（例如http请求行、头）

使用关联数据进行认证加密（用AEAD表示）是为了解决想对整个消息完成认证功能，而只对消息的部分实现加密的问题。例如http报文中只加密body部分。

加密：**AEAD(K,P,A)=(C,A,T)**，身份认证标签依赖于P和A，且只有在C和A都没有被修改的情况下才会被认证为有效。

解密：**ADAD(K,C,A,T)=(P,A)**，可以看出无论是密文C损坏还是关联数据A损坏，都无法完成解密。

如果想保证对同一明文输出的结果是不同的，可以加入nonce参与运算，即：

ADAE(K,P,A,N)

ADAD(K,C,A,T,N)=(P,A)

如果关联数据A为空，AEAD算法就是一个普通的认证加密；如果P是空的，可以当做MAC使用。

AES-GCM

AES-GCM基于AES算法，采用了Galois计数器模式（GCM，分组密码的一种工作方式），GCM是对CTR的改进。

AES-GCM本质上是一种先加密后MAC的结构，其中的AES-CTR使用128比特密钥（K）和96比特nonce（N）进行加密，但它的计数器从1开始而不是0。

原理如下图：（表示与H进行多项式乘法）

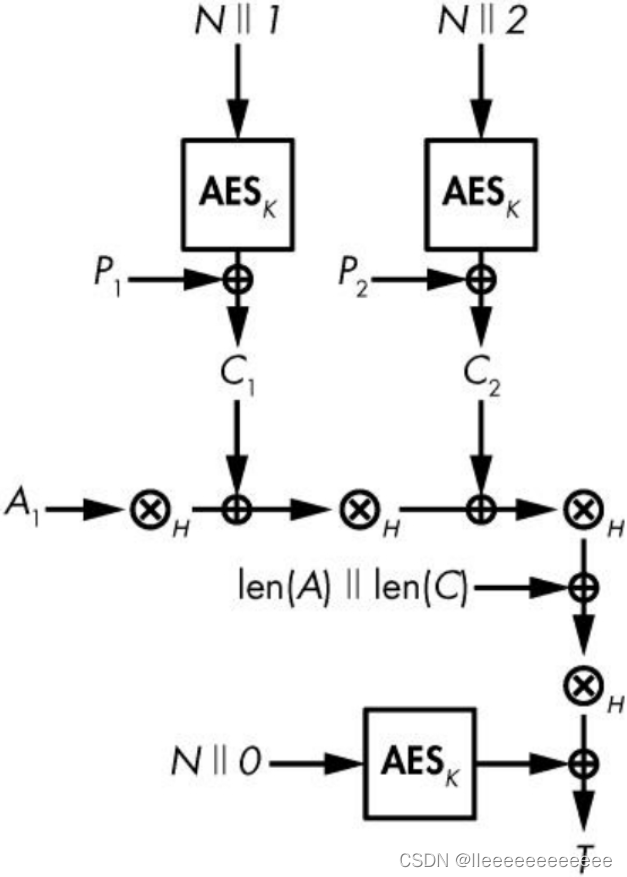
过程（GHASH是一个通用哈希函数，对应于上图的一系列多项式乘法）：

1.将明文P分组，由密钥K计算认证密钥H=AES(K,0)，计算M0=GHASH(H,A1)。

2.计算C1=AES(K,N || 1) ⊕ P1，M1=GHASH(H,C1 ⊕ M0)

3.计算C2=AES(K,N || 2) ⊕ P2，M2=GHASH(H,C2 ⊕ M1)，以此类推，计算到最后一个分组得到Mn。

4.计算L=len(A) || len(C)，计算ML=GHASH(H,L ⊕ Mn)

5.计算T=AES(K,N || 0) ⊕ ML

到此整个计算过程结束，其中len(A)指的是关联数据A的长度，len(C)指的是密文C的长度。

GCM使用了Wegman-Carter MAC。它将值AES(K,N || 0)与名为GHASH的通用哈希函数的输出值进行异或。

GCM没有直接使用K，以确保如果GHASH的密钥被泄露，主密钥K仍然是保密的。H=AES(K,0)，这个过程不可逆，即无法通过H来恢复K。

多项式乘法

现在有两个多项式(1+X+X^2)和(X+X^3)，需要计算它们的的乘积。首先要对这两个多项式做普通的多项式乘法，计算结果如下（两个X^3项可以相互抵消）：

使用模运算来压缩上述结果，即对多项式X+X2+X4+X5作模1+X3+X4运算，返回结果X2。

因为多项式A+BC模B后等于A（A<B），所以X+X^2+X^4+X^5可以视为(1+X^3+X^4)与X的乘积再加上X^2，即X+X^2+X^4+X^5=X⊗(1+X^3+X^4)+X^2。

安全性

AES-GCM容易遭受nonce重放攻击。如果在两次AES-GCM实现中使用相同的nonce（N），攻击者就可以获得身份认证密钥H，然后可以使用H为任何密文、关联数据或其组合伪造标签。

标签（T）计算：T=GHASH(H,A,C) ⊕ AES(K,N || 0)。

现在用相同的nonce N计算出两个标签：

T1=GHASH(H,A1,C1)⊕AES(K,N||0)

T2=GHASH(H,A1,C1)⊕AES(K,N||0)

对它们相异或就得到了如下结果：

可以看到AES计算的部分已经被消掉了，然而GHASH是线性的，很容易破解H。

OCB（偏移码本模式）

OCB也是分组密码工作的一种方式，近些年才放开非军事软件的免费许可。

OCB对每个明文分组P进行加密得到相应的密文分组C=E(K,P ⊕ O) ⊕ O，其中E是用以实现加密功能的分组密码算法。O（称为偏移量）是一个依赖于密钥K和nonce的值，其中nonce是随着处理的分组个数的增加而递增的。

计算T：

先计算S=P1⊕P2⊕P3⊕...Pn。

T=E(K,S⊕O*)，其中的O*是由上一个被处理的明文分组的偏移值所计算出的新偏移值。

下图为OCB的原理图（只画了2个分组，无关联数据的情况）：

当包含关联数据Ai（关联数据可以分组）时，标签T计算方式为：

T= E(K, S ⊕ O*) ⊕ E(K, A1 ⊕ O1) ⊕ E(K, A2 ⊕ O2) ⊕...⊕ E(K, An ⊕ On)

基于置换的AEAD

计算方式（P()为置换函数，N为nonce，S为内部状态，H0为初始状态）：

S1=P(H0 ⊕ (K || N))，C1=S1 ⊕ P1

S2=P(S1)，C2=S2 ⊕ P2

以此类推，Sn=P(S(n-1))，Cn=Sn ⊕ Pn

T=P(Sn)

计算原理如下图所示：