深度学习——CNN实现MNIST手写数字的识别

活动地址：CSDN21天学习挑战赛

知识点介绍

MNIST

介绍

MNIST是机器学习的入门数据集，全称是 Mixed National Institute of Standards and Technology database ，来自美国国家标准与技术研究所，是NIST（National Institute of Standards and Technology）的缩小版

训练集（training set）由来自 250 个不同人手写的数字构成，其中 50% 是高中学生，50% 来自人口普查局（the Census Bureau）的工作人员，数量为60000

测试集（test set）也是同样比例的手写数字数据，数量为10000

总共有70000个数据

下载

MNIST数据集可以在 **MNIST官网 **中下载,也可以之间通过keras库导入(后面采用的是这种)

具体有4个压缩包，如下：
    下载解压后放入**工作目录**即可
keras库导入
from keras import datasets
# 导入数据集
(train_images, train_labels), (test_images, test_labels) = datasets.mnist.load_data()  # datasets内部集成了MNIST数据集

数据的简单处理

MNIST数据集共有70000张图片，图片的规格均是28*28，所以一张图片的像素值为784

故以传统神经网络来看, 可以设置二维数组[70000][784]，而每张图片每个像素点值介于 0~~1 之间,即数组元素值在0~~1之间

CNN神经网络

K同学啊的神经网络程序流程

而卷积神经网络CNN则对上图的神经网络进行了优化，解决了传统神经网络参数过多导致的难以处理、效率低、过拟合的问题

CNN的作用

卷积神经网络CNN可以处理大多数的计算机视觉问题

1.可以用来完成检测任务：检测图像中有什么

** 2.可以完成检索和分类任务**
分类则是获取图像信息的类别，检索则是根据某图像获取相似的图像
3.可以实现超分辨率重构，提高图像的清晰度

4.可以实现OCR、无人驾驶、人脸识别等高新技术

CNN的主要特征

传统神经网络是将图像转换成向量处理，每个像素点值在 0~1 内变化

而CNN不再将图像按向量处理，而是输入即是三维数据（** $h \times w \times c$ ** 其中h、w为图像的长、宽，c为图像的通道数，rgb图像有r、g、b三个通道，每个通道都要单独处理）

CNN由于是进行三维数据的处理，所以一般用GPU（图像处理器）更快

CNN的神经网络结构

输入层：图像数据输入到训练网络中

卷积层：根据所规定的卷积核大小和卷积步长分割每个通道的数据，根据每个通道当前特有的权重值，按内积计算分割的每部分的特征值，最后将各个通道相对应的分割部分所得到的特征值相加，再加上偏置参数，即可得到当前卷积的特征图** “特征提取”**

输入为 $7\times 7\times3$ ，（实际输入数据是 $5\times 5\times 3$ ,这里由于边缘效应，进行了**+pad 1的边缘填充，变成了 $7\times 7\times 3$ ），卷积核为 ****** $3\times 3\times 3$ ****，卷积步长为2，卷积核个数为2。

我们先来看第一个特征图的计算(卷积核是W0)，第二个特征图也是如此(卷积核是W1)：

池化层：池化就是特征值的取舍，一般是根据最大池化法对特征图进行压缩** “特征压缩”**

一般是采用最大池化法进行计算：具体思想是取每块中最大的特征值作为最后的特征值
  4*4      -->   2*2 
1 2 5 7          6 9
3 6 9 5          4 6 
4 2 3 5
1 4 3 6
// 每4个中取最大，左上，左下，右上，右下
全连接层：对得到的多个特征图进行转换，映射到样本标记空间** “特征分类”**

输出层：输出训练结果

数据输入—>特征提取—>特征压缩—>特征分类—>结果输出

CNN的相关参数

卷积步长（滑动窗口步长）：指的是卷积核在通道数据上每次移动多少个单位数据

  步长越小，得到的结果越精确，但训练效率也越低

  **一般图像处理，步长选1 ; 文本处理,步长一般不是1**

**卷积核尺寸 : 指的是通道数据每多少个计算一个特征值 **

  卷积核尺寸越小,得到的结果越精确,但训练效率也越低

 ** 一般取 ******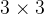![3\times 3](https://latex.csdn.net/eq?3%5Ctimes%203)********

边缘填充 :

  当卷积层计算特征值是每次移动会有部分数据重复使用,这样的话**越在边缘的参与计算的 次数越少,而越中间的计算的次数越多,**为了尽量减少图像数据计算次数的相差,我们可以在外部**加若干层不影响计算结果的0,**这样则图像的真实数据参与特征值的计算次数就相差会很小

**  一般是边缘填充取1,即外加一层0**

卷积核数

** 卷积核数即最后的特征图数**

特征图宽高计算

** $h=\frac{H_o-h_c+2p}{d}+1$ $w=\frac{W_o-w_c+2p}{d}+1$ **

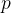    其中![W_o,H_o](https://latex.csdn.net/eq?W_o%2CH_o) 是输入图像的宽高,![w_c,h_c](https://latex.csdn.net/eq?w_c%2Ch_c) 是卷积核的宽高,![p](https://latex.csdn.net/eq?p)是边缘填充数,d是步长

参数数量计算

** 卷积层的参数数量为: 所有的矩阵参数+ 偏置参数**

  例如 ![5\times 5\times 3\times 10](https://latex.csdn.net/eq?5%5Ctimes%205%5Ctimes%203%5Ctimes%2010) 的卷积核有10个,则有10个偏置参数共![5\times 5\times 3\times 10 +10](https://latex.csdn.net/eq?5%5Ctimes%205%5Ctimes%203%5Ctimes%2010%20&amp;plus;10)

  760个

神经网络层数

  神经网络层数是指有需要参数运算的层,**比如卷积层和全连接层,**

** 池化层不在计算范围内**

MNIST识别的网络结构

K同学啊所采用的网络结构:

该网络结构是3层的神经网络,一次卷积后根一次池化,共有两次卷积池化

输入层输入的是 $28\times 28\times 1$ ,只有一个通道

(因为图像边缘信息不重要这里并没有进行边缘填充)

第一次卷积,卷积核共32个,卷积核的规格是 $3\times 3\times 1$ ,步长为1
        ![H=\frac{28-3+2\times 0}{1}+1=26](https://latex.csdn.net/eq?H%3D%5Cfrac%7B28-3&amp;plus;2%5Ctimes%200%7D%7B1%7D&amp;plus;1%3D26)    ![W=\frac{28-3+2\times 0}{1}+1=26](https://latex.csdn.net/eq?W%3D%5Cfrac%7B28-3&amp;plus;2%5Ctimes%200%7D%7B1%7D&amp;plus;1%3D26)
第一次池化,采用每4个数据进行一次最大池化,即宽高压缩到原来的0.5倍,步长为2

第二次卷积,卷积核为64个,规格不变,步长不变
        ![H=11,W=11](https://latex.csdn.net/eq?H%3D11%2CW%3D11)  计算方法同上
第二次池化,池化规格不变

relu层:Relu是一个激活函数,卷积层完执行该函数,作用:去除卷积结果中的负值,保留正值不变

Flatten层,将特征图展成向量,全连接层进行特征分类,再输出结果

CNN识别MNIST程序

前期准备

导入库

import tensorflow as tf
from keras import datasets, layers, models  # 这里keras版本是2.8.0
import matplotlib.pyplot as plt

设置采用电脑GPU训练


# 设置采用GPU训练程序
gpus = tf.config.list_physical_devices("GPU")  # 获取电脑GPU列表
if gpus:  # gpus不为空
    gpu0 = gpus[0]  # 选取GPU列表中的第一个
    tf.config.experimental.set_memory_growth(gpu0, True)  # 设置GPU显卡按需使用
    tf.config.set_visible_devices([gpu0], "GPU")  # 设置GPU可见的设备清单，默认是都可见，这里只设置了gpu0可见

导入数据

# 导入数据集
(train_images, train_labels), (test_images, test_labels) = datasets.mnist.load_data()  
# datasets内部集成了MNIST数据集

数据归一化

归一化和标准化

  归一化与标准化是**数据集数据缩放**的两种形式,可以起到的作用如下

  1. 使不同的量纲处于同一数量级,减小方差大的数据的影响,模型更加准确

  2. 相比大数,较小的数使得数据运算处理更加容易,提高算法的效率

** 归一化: 采用下列公式,使用最大值和最小值,将数据集的数据缩放****到 [0,1] 中 ** $x=\frac{x_i-x_{min}}{x_{max}-x_{min}}$

                 **根据公式,图像若采用归一化,rgb最大值为255,最小值为0,故即为 ******![{\color{Red}\frac{x_i}{255}}](https://latex.csdn.net/eq?%7B%5Ccolor%7BRed%7D%5Cfrac%7Bx_i%7D%7B255%7D%7D)********

** **标准化: 可以采用下列公式,使用均值和标准差,将数据压缩到一个小的特定区间中

** $x=\frac{x_i-\mu }{\sigma }$ **

** 公式不唯一**** **

from mpmath.identification import transforms

transforms.Normalize(mean = (0.485, 0.456, 0.406), std = (0.229, 0.224, 0.225)) 
# 这三个通道的mean std需要自己计算

代码

# 归一化
# 将像素的值标准化至0到1的区间内,rgb像素值 0~255 0为黑 1为白
train_images, test_images = train_images / 255.0, test_images / 255.0

调整数据格式

根据数据集大小选择数据格式(个数,宽,高,通道数)
# 根据数据集大小调整数据到我们需要的格式
print(train_images.size)  # 47040000
print(test_images.size)  # 7840000
train_images = train_images.reshape((60000, 28, 28, 1))
test_images = test_images.reshape((10000, 28, 28, 1))
这里的47040000和7840000并不支持我们构建三通道

构建CNN网络模型

利用models包内的Sequential方法建立顺序模型

这里选择了三层神经网络:2层卷积池化 1层Flatten 1层全连接然后输出

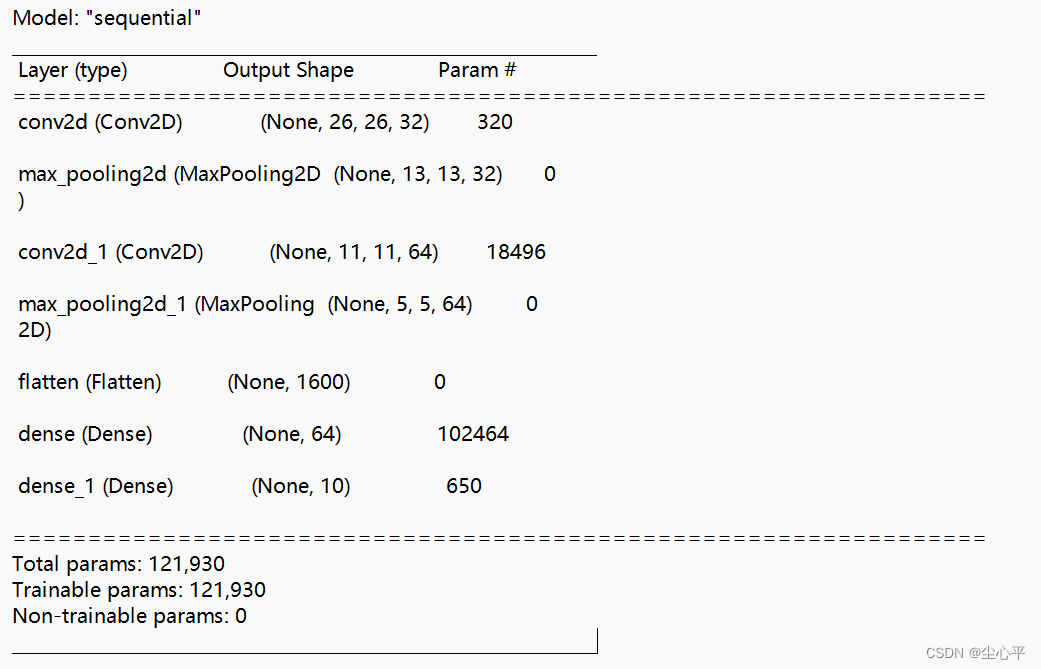
# 构建CNN网络模型
model = models.Sequential([  # 采用Sequential 顺序模型
    layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)),
    # 卷积层1，卷积核个数32，卷积核3*3*1 relu激活去除负值保留正值，输入是28*28*1
    layers.MaxPooling2D((2, 2)),  # 池化层1，2*2采样

    layers.Conv2D(64, (3, 3), activation='relu'),
    # 卷积层2，卷积核64个，卷积核3*3，relu激活去除负值保留正值
    layers.MaxPooling2D((2, 2)),  # 池化层2，2*2采样
    
    layers.Flatten(),  # Flatten层，连接卷积层与全连接层
    layers.Dense(64, activation='relu'),  # 全连接层，64张特征图，特征进一步提取
    layers.Dense(10)  # 输出层，输出预期结果
])
# 打印网络结构
model.summary()

网络结构如下:

CNN网络结构

激活函数

激活函数可以实现数据的非线性变换,使得神经网络可以实现应用到更多的非线性模型中

为什么要使用激活函数

常用的激活函数:

** Sigmoid函数**

优点：非常适合用作输出层，并且比较容易求导。

缺点：计算机求解时相对比较耗时，对于规模比较大的深度网络，会较大地增加训练时间。

Softmax函数

Relu函数

Relu函数目前使用最为频繁

** Tanh函数**

相似于Sigmoid,减少了迭代次数,但幂运算问题仍存在,仍有耗时问题

编译CNN网络模型

采用models包内的compile函数进行编译

编译需要设置优化器,损失函数以及metrics

优化器

优化器是对参数的优化,指的是更新神经网络模型参数所使用的算法

常用的优化器有以下几种:

BDG 批量梯度下降

优点：可以得到全局最优解；易于并行实现；迭代次数比较少。
缺点：数据集较大时,训练很慢

SGD 随机梯度下降

优点：训练速度快；
缺点：准确度下降，并不是全局最优；不易于并行实现。从迭代次数来看，SGD迭代次数较多，在解空间的搜索过程看起来很盲目。

MBGD 小批量梯度下降

优点：收敛更稳定，另一方面可以充分地利用深度学习库中高度优化的矩阵操作来进行更有效的梯度计算。
缺点：关于学习率的选择，如果太小，收敛速度就会变慢，如果太大，损失函数就会在极小值处不停的震荡甚至偏离。

Momentum 动量算法

Nesterov动量

是对Momentum的改进,提高了灵敏度,但人工设置的学习率非常生硬

Adam

优点:Adam在很多情况下算作默认工作性能比较优秀的优化器

缺点:可能会不收敛,错过全局最优解

一般用adam,效果不好再找其他优化器

损失函数

损失函数是一种衡量损失和错误程度的函数,损失越小,模型越好

MSE 均方差
MAE 平均绝对误差
MAPE 相对百分误差
MSLE 对MSE加一层对数的优化
KLD = KL散度从预测值概率分布Q到真值概率分布P的信息增益,用以度量两个分布的差异。
cosine 预测值与真实标签的余弦距离平均值的相反数。
binary_crossentropy 对数损失，logloss
categorical_crossentropy 多类的对数损失
sparse_categorical_crossentrop：和 categorical_crossentropy一样，但接受稀疏标签

metrics

在深度学习中，性能指标(Metrics)是衡量一个模型好坏的关键，通过衡量模型输出y_predict 和 y_true之间的某种"距离"得出的。

keras提供了六个性能指标函数

accuracy

binary_accuracy

categorical_accuracy

sparse_categorical_accuracy

top_k_categorical_accuracy

sparse_top_k_categorical_accuracy

代码

# 编译
model.compile(optimizer='adam',  # 优化器
              loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),  # 设置损失函数 from_logits: 为True时，会将y_pred转化为概率
              metrics=['accuracy'])

采用adam优化器, sparse_categorical_crossentrop损失函数,metrics采用accuracy

训练CNN网络

history = model.fit(train_images, train_labels, epochs=10,
                    validation_data=(test_images, test_labels))
# validation_data关键字传参为测试集数据
# epochs为训练轮数,这里是10轮
epochs为训练轮数,在梯度下降的模型训练的过程中，神经网络逐渐从不拟合状态到优化拟合状态，达到最优状态之后会进入过拟合状态。因此epoch并非越大越好，一般是指在50到200之间。数据越多样，相应epoch就越大。

预测

1.绘制测试集图片(取前20张),判断预测是否正确

# 绘制测试集图片
plt.figure(figsize=(20, 10))  # 这里只看20张，实际上并不需要可视化图片这一步骤
for i in range(20):
    plt.subplot(5, 10, i + 1)
    plt.xticks([])
    plt.yticks([])
    plt.grid(False)
    plt.imshow(test_images[i], cmap=plt.cm.binary)
    plt.xlabel(test_labels[i])
plt.show()

测试集的前20张图片

为什么要使用激活函数

2.预测

# 预测
pre = model.predict(test_images)  # 对所有测试图片进行预测
for x in range(5):
    print(pre[x]) #输出预测的0-9的每个的得分情况,越正越可能,越负越不可能

得分情况越正越可能,越负越不可能

分析得分得前五张图片预测为 7 2 1 0 4

也可以直接得到预测结果

修改预测代码如下:

# 预测
pre = model.predict(test_images)  # 对所有测试图片进行预测
for x in range(5):
    print(pre[x])
for x in range(5):
    print(np.array(pre[x]).argmax()) #得到最大值的索引

预测结果:

源码

import numpy as np
import tensorflow as tf
from keras import datasets, layers, models  # 这里keras版本是2.8.0
import matplotlib.pyplot as plt

# 设置采用GPU训练程序
gpus = tf.config.list_physical_devices("GPU")  # 获取电脑GPU列表
if gpus:  # gpus不为空
    gpu0 = gpus[0]  # 选取GPU列表中的第一个
    tf.config.experimental.set_memory_growth(gpu0, True)  # 设置GPU显卡按需使用
    tf.config.set_visible_devices([gpu0], "GPU")  # 设置GPU可见的设备清单，默认是都可见，这里只设置了gpu0可见

# 导入数据集
(train_images, train_labels), (test_images, test_labels) = datasets.mnist.load_data()  # datasets内部集成了MNIST数据集，

# 归一化
# 将像素的值标准化至0到1的区间内,rgb像素值 0~255 0为黑 1为白
train_images, test_images = train_images / 255.0, test_images / 255.0

# 根据数据集大小调整数据到我们需要的格式
print(train_images.size)  # 47040000
print(test_images.size)  # 7840000
train_images = train_images.reshape((60000, 28, 28, 1))
test_images = test_images.reshape((10000, 28, 28, 1))

# 构建CNN网络模型
model = models.Sequential([  # 采用Sequential 顺序模型
    layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)),
    # 卷积层1，卷积核个数32，卷积核3*3*1 relu激活去除负值保留正值，输入是28*28*1
    layers.MaxPooling2D((2, 2)),  # 池化层1，2*2采样

    layers.Conv2D(64, (3, 3), activation='relu'),
    # 卷积层2，卷积核64个，卷积核3*3，relu激活去除负值保留正值
    layers.MaxPooling2D((2, 2)),  # 池化层2，2*2采样

    layers.Flatten(),  # Flatten层，连接卷积层与全连接层
    layers.Dense(64, activation='relu'),  # 全连接层，64张特征图，特征进一步提取
    layers.Dense(10)  # 输出层，输出预期结果
])
# 打印网络结构
model.summary()

# 编译
model.compile(optimizer='adam',  # 优化器
              loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
              # 设置损失函数from_logits: 为True时，会将y_pred转化为概率
              metrics=['accuracy'])

# 训练
# epochs为训练轮数
history = model.fit(train_images, train_labels, epochs=10,
                    validation_data=(test_images, test_labels))
print(history)
# 绘制测试集图片
plt.figure(figsize=(20, 10))  # 这里只看20张，实际上并不需要可视化图片这一步骤
for i in range(20):
    plt.subplot(5, 10, i + 1)
    plt.xticks([])
    plt.yticks([])
    plt.grid(False)
    plt.imshow(test_images[i], cmap=plt.cm.binary)
    plt.xlabel(test_labels[i])
plt.show()

# 预测
pre = model.predict(test_images)  # 对所有测试图片进行预测
for x in range(5):
    print(pre[x])
for x in range(5):
    print(np.array(pre[x]).argmax())

标签： python 深度学习 tensorflow

本文转载自: https://blog.csdn.net/weixin_53966032/article/details/126112330
版权归原作者凪廾所有，如有侵权，请联系我们删除。