交互式多模型-粒子滤波IMM-PF—在机动目标跟踪中的应用/matlab实现
原创不易,路过的各位大佬请点个赞
WX: ZB823618313
交互式多模型-粒子滤波IMM-PF—在机动目标跟踪中的应用/matlab实现
1. 对机动目标跟踪的理解
机动目标跟踪一直是目标跟踪领域研究的难点和重点问题。建立目标运动模型和滤波算法是目标跟踪的两个重要因素。由于目标的机动具有不可预测性,使得我们很难建立精确的目标运动模型。如何建立一种有效的模型来反映目标真实的运动轨迹是高机动目标跟踪系统急需解决的问题。经过近三十年的研究,该领域取得了许多重要成果。
个人理解:机动目标跟踪拥有三要素:
1) 机动目标跟踪建模
2) 传感器测量
3) 滤波器设计
1) 机动目标跟踪建模
机动目标模型描述了目标状态随着时间变化的过程。文献[1]指出,一个好的模型抵得上大量的数据。当前几乎所有的目标跟踪算法都是基于模型进行状态估计的。在卡尔曼滤波器被引入目标跟踪领域后,基于状态空间的机动目标建模成为主要研究对象之一。目标的空间运动基于不同的运动轨迹和坐标系,可分为-维、二维和三维运动。而根据不同方向的运动是否相关,目标机动模型可分为坐标间不耦合模型和坐标间耦合模型。
匀速运动模型CV
匀加速运动模型CA
匀速转弯模型CT
当前统计模型CS
Singer模型
Jerk模型
…
2) 传感器测量
测量一般分为在
笛卡尔坐标系:惯导、激光雷达、ADS-B数据
极坐标/球坐标:雷达、声纳、相控阵雷达
混合坐标系:雷达+INS
大地坐标系:GPS、经纬仪、ADS-B数据
…
3) 滤波算法
从算法层面,在目标跟踪系统中,常用的滤波算法是以卡尔曼滤波器为基本框架的估计算法。卡尔曼滤波器是一种线性、无偏、以误差均方差最小为准则的最优估计算法,它有精确的数学形式和优良的使用效能。卡尔曼滤波方法实质上是一种数据处理方法,它采用递推滤波方法,根据获取的量测数据由递推方程递推给出新的状态估计。由于计算量和存储量小,比较容易满足实时计算的要求,在工程实践中得到广泛应用。
除此之外,非线性滤波也广泛应用与机动目标跟踪,比如:
卡尔曼滤波
非线性滤波+自适应模型
扩展卡尔曼滤波EKF
无迹卡尔曼滤波UKF
容积卡尔曼滤波CKF
求积卡尔曼滤波QKF
中心差分卡尔曼滤波CDKF
Divided difference filter DDF
高斯混合滤波GSF
强跟踪滤波STF
粒子滤波PF
… …
自适应多模型方法
自主式多模型方法
协作式多模型方法:GPB、IMM
变结构多模型方法
… …
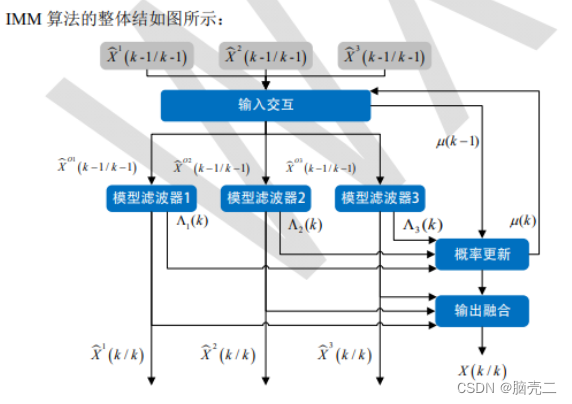
2. 交互式多模型IMM
在现代目标跟踪系统中,对于运动模型基本不改变的运动目标,即系统的状态转移方程和观察方程都是线性的,那么在线性最小均方误差(LMMSE)的意义下,采用α-β滤波、Kalman滤波等线性滤波算法可以得到良好的滤波效果。但是对于机动目标跟踪,由于其运动状态的不确定性,效果不好。所以提出交互式多模型(IMM)的自适应机动目标跟踪算法:
在机动目标跟踪方法中,为避免具有机动检测的跟踪算法产生的估计时间延迟和机动检测过程中跟踪性能的降低,采用基于交互式多模型(IMM)的自适应机动目标跟踪算法,通过2个目标模型的交互作用来实现对目标机动状态的自适应估计。在工程上,将基于CV和"当前"统计模型的IMM算法应用在某导航雷达跟踪系统中,经验证IMM算法对匀速直线运动、机动运动目标跟踪均能取得较好的效果。
核心思想: IMM算法的基本思想是用多个不同的运动模型匹配机动目标的不同运动模式,不同模型间的转移概率是–个马尔可夫矩阵,目标的状态估计和模型概率的更新使用卡尔曼滤波。

3、 粒子滤波PF
核心思想:是使用一组具有相应权值的随机样本(粒子)来表示状态的后验分布。该方法的基本思路是选取一个重要性概率密度并从中进行随机抽样,得到一些带有相应权值的随机样本后,在状态观测的基础上调节权值的大小。和粒子的位置,再使用这些样本来逼近状态后验分布,最后将这组样本的加权求和作为状态的估计值。粒子滤波不受系统模型的线性和高斯假设约束,采用样本形式而不是函数形式对状态概率密度进行描述,使其不需要对状态变量的概率分布进行过多的约束,因而在非线性非高斯动态系统中广泛应用。尽管如此,粒子滤波目前仍存在计算量过大、粒子退化等关键问题亟待突破。
通常情况下选择先验分布作为重要性密度函数、即
q
(
x
k
∣
x
k
−
1
(
i
)
,
z
k
)
=
p
(
x
k
∣
x
k
−
1
(
i
)
)
q(x_k |x_{k-1}^{(i)}, z_{k})=p(x_k |x_{k-1}^{(i)})
q(xk∣xk−1(i),zk)=p(xk∣xk−1(i))
对该函数取重要性权值为
w
k
(
i
)
=
w
k
−
1
(
i
)
p
(
z
k
∣
x
k
(
i
)
)
w_k^{(i)}=w_{k-1}^{(i)}p(z_k |x_{k}^{(i)})
wk(i)=wk−1(i)p(zk∣xk(i))
同样
w
k
(
i
)
w_k^{(i)}
wk(i)需要归一化得到
w
~
k
(
i
)
\tilde{w}_k^{(i)}
w~k(i)。
标准的粒子滤波算法步骤为:
粒子滤波PF:
Step 1: 根据p ( x 0 ) p(x_{0}) p(x0)采样得到 N N N个粒子 x 0 ( i ) ∼ p ( x 0 ) x_0^{(i)} \sim p(x_{0}) x0(i)∼p(x0)For
i = 2 : N i=2:N i=2:NStep 2: 根据状态转移函数产生新的粒子为:$
x k ( i ) ∼ p ( x k ∣ x k − 1 ( i ) ) x_k^{(i)} \sim p(x_{k} |x_{k-1}^{(i)}) xk(i)∼p(xk∣xk−1(i))Step 3: 计算重要性权值:
w k ( i ) = w k − 1 ( i ) p ( z k ∣ x k ( i ) ) w_k^{(i)}=w_{k-1}^{(i)}p(z_k |x_{k}^{(i)}) wk(i)=wk−1(i)p(zk∣xk(i))Step 4: 归一化重要性权值:
w ~ k ( i ) = w k ( i ) ∑ j = 1 N w k ( j ) \tilde{w}_k^{(i)}=\frac{w_k^{(i)}}{\sum_{j=1}^Nw_k^{(j)}} w~k(i)=∑j=1Nwk(j)wk(i)Step 5: 使用重采样方法对粒子进行重采样(以系统重采样为例)
Step 6: 得到k k k时刻的后验状态估计: E [ x ^ k ] = ∑ i = 1 N x k ( i ) w ~ k ( i ) E[\hat{x}_{k}]= \sum_{i=1}^Nx_{k}^{(i)}\tilde{w}_k^{(i)} E[x^k]=i=1∑Nxk(i)w~k(i)End For
粒子滤波PF算法结构图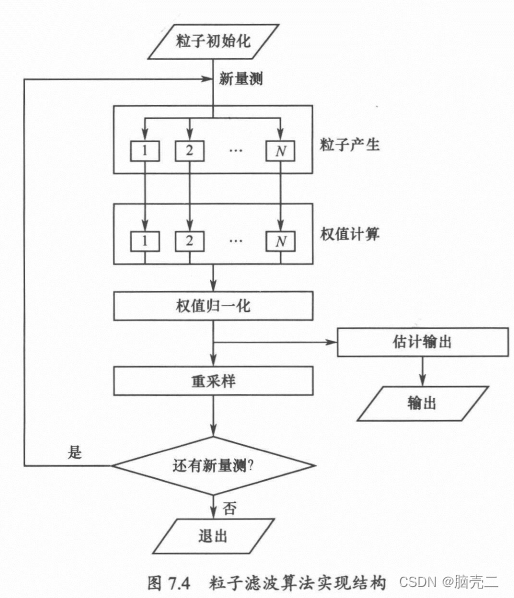
算法:系统重采样 (systematic resampling)
Fori = 1 : N i=1:N i=1:NStep 1: 初始化累积概率密度函数CDF:
c 1 = 0 c_1=0 c1=0For
i = 2 : N i=2:N i=2:NStep 2: 构造CDF:
c i = c i − 1 + w k ( i ) c_i=c_{i-1}+w_k^{(i)} ci=ci−1+wk(i)Step 3: 从CDF的底部开始:
i = 1 i=1 i=1Step 4: 采样起始点:
u 1 = U [ 0 , 1 / N ] u_1=\mathcal{U}[0,1/N] u1=U[0,1/N]End For
Forj = 1 : N j=1:N j=1:NStep 5: 沿CDF移动:
u j = u 1 + ( j − 1 ) / N u_j=u_{1}+(j-1)/N uj=u1+(j−1)/NStep 6: While
u j > c i u_j>c_i uj>ci i = i + 1 i=i+1 i=i+1End While
Step 7: 赋值粒子:x k ( j ) = x k ( i ) x_k^{(j)}=x_k^{(i)} xk(j)=xk(i)Step 8: 赋值权值:
w k ( j ) = 1 / N w_k^{(j)}=1/N wk(j)=1/NStep 9: 赋值父代:
i ( j ) = i i^{(j)}=i i(j)=iEnd For
4、 交互式多模型-粒子滤波IMM-PF
目前, IMMPF算法在目标跟踪领域已取得了长足的进展,并逐渐延伸到故障诊断等领域,形成了一些有价值的理论和实践成果。但是,这些理论和应用实践相对庞杂,特别是IMMPF算法本身还出现了一些不同的分支,使得对该算法的系统理解和掌握存在一些困难。
4.1、 核心思想
把PF应用到IMM算法的最主要的问题在于如何实现PF到IMM算法框架中基于高斯假设滤波(如KF、UKF、EKF等)的替换,换句话说就是如何用PF替换KF,并保证替换以后算法的其他相关步骤的合理性。
卡尔曼滤波和粒子滤波的相同点:在于它们都需要以目标当前时刻的测量过程噪声方差和测量方差作为其输入条件。
卡尔曼滤波和粒子滤波的不同点:卡尔曼滤波是基于“高斯噪声、线性系统”的假设条件,初始输入条件是前一时刻的状态均值和协方差,输出的是更新后的状态估计和协方差;而粒子滤波不以“高斯噪声、线性系统”为其假设条件,其初始条件是粒子群,输出是更新后的粒子云和状态估计。
4.2、存在的问题
- 1)交互/混合的问题 经典IMM 算法交互过程以前一次运算的估计算满足各子模型滤波的初始条件,该初始条件决定了系统的滤波精度。按照这一思想,IMMPF算法交互的目的在于如何以上次运算的粒子群为参数,获取各PF的初始粒子,使得这些粒子经过滤波以后能够更准确地实现对后验概率密度函数的近似。
- 2)模型概率的计算问题 经典IMM算法模型概率更新的基础是模型似然度的计算,通常需要计算各模型的残差、协方差。设条件,经过PF滤波之后的后验粒子通常不符合正态分布,因而失去了上述“残差、协方差”的理论基础。所以,如何建立基于粒子的模型概率更新方法也是一个很重要的问题。
4.3、解决思路
目前关于多模型粒子滤波算法的研究基本上都围绕上述问题展开。McGinnity S和 Neil Gordon最早提出将粒子滤波和多模型方法相结合用于跟踪问题l8-9,随后很多学者在该问题上做了大量的研究,并取得了一定的理论成果。
主要分为3个方面:
- 1)基于高斯假设的IMMPF算法
- 2) 纯粒子的 IMMPF算法
- 3)基于上述算法的其他改进算法。
其中第一种也是比较简单的IMM-PF组合方法。基于高斯假设,PF中就可以算出量测预测
z ^ k ∣ k − 1 \hat{z}_{k|k-1} z^k∣k−1 和 新息协方差 S k S_k Sk,这样PF和就和标准的高斯假设滤波器KF比较相近,容易计算局部滤波器的模型概率。
基于高斯假设的IMMPF算法把交互式多模型方法与高斯和粒子滤波相结合,也可称为交互式高斯和粒子滤波(IMM - CSPF),其理论基础是“高斯和"理论。
注意:不同与IMM与KF的组合,IMM和PF的组合并不是直接加和起来就好了,后者需要解决:模型概率计算问题、交互式估计与局部估计器粒子连接问题、似然概率计算问题、各局部滤波器初始粒子确定问题等等。这些问题,有兴趣的童鞋认真看看论文,公式版本太多,我也讲不清楚。
下面提供的仿真结果及代码是基于第一种方法的IMM-PF,也是最常见和标准的一种IMM-PF滤波算法。
5. IMM-PF在机动目标跟踪中的应用——matlab场景一
5.1. 仿真过程
一、目标模型:CV CT CV
第一阶段:1:39s,匀速运动CV
第二阶段:40:91s,匀速圆周运动CT,角速度:
2
∗
π
/
180
;
2*\pi/180;
2∗π/180;
第三阶段:92:99s,匀速运动CV
第四阶段:100:131s,匀速圆周运动CT,角速度:
−
3
∗
π
/
180
;
-3*\pi/180;
−3∗π/180;
第五阶段:132:150s,匀速运动CV
CV模型:(细节见另一个博客)
X
k
+
1
=
[
1
T
0
0
0
1
0
0
0
0
1
T
0
0
0
1
]
X
k
+
[
T
2
/
2
0
T
0
0
T
2
/
2
0
T
]
W
k
X_{k+1}=\begin{bmatrix}1&T&0&0\\0&1&0&0\\0&0&1&T\\0&0&0&1 \end{bmatrix}X_{k} + \begin{bmatrix}T^2/2&0\\T&0\\0&T^2/2\\0&T\end{bmatrix}W_k
Xk+1=⎣⎢⎢⎡1000T100001000T1⎦⎥⎥⎤Xk+⎣⎢⎢⎡T2/2T0000T2/2T⎦⎥⎥⎤Wk
CT模型:(细节见另一个博客)
X
k
+
1
=
[
1
sin
(
ω
T
)
ω
0
−
1
−
cos
(
ω
T
)
ω
0
cos
(
ω
T
)
0
−
sin
(
ω
T
)
0
1
−
cos
(
ω
T
)
ω
1
sin
(
ω
T
)
ω
0
sin
(
ω
T
)
0
cos
(
ω
T
)
]
X
k
+
[
T
2
/
2
0
T
0
0
T
2
/
2
0
T
]
W
k
X_{k+1}=\begin{bmatrix}1&\frac{\sin(\omega T)}{\omega}&0&-\frac{1-\cos(\omega T)}{\omega}\\0&\cos(\omega T)&0&-\sin(\omega T)\\0&\frac{1-\cos(\omega T)}{\omega}&1&\frac{\sin(\omega T)}{\omega}\\0&\sin(\omega T)&0&\cos(\omega T)\end{bmatrix}X_{k} + \begin{bmatrix}T^2/2&0\\T&0\\0&T^2/2\\0&T\end{bmatrix}W_k
Xk+1=⎣⎢⎢⎡1000ωsin(ωT)cos(ωT)ω1−cos(ωT)sin(ωT)0010−ω1−cos(ωT)−sin(ωT)ωsin(ωT)cos(ωT)⎦⎥⎥⎤Xk+⎣⎢⎢⎡T2/2T0000T2/2T⎦⎥⎥⎤Wk
初始状态:
x
0
=
[
30000
,
80
,
20000
,
50
]
T
P
0
=
diag
(
[
1
e
6
,
1
e
2
,
1
e
6
,
1
e
2
]
)
x_0=[30000, 80, 20000, 50]^T\\ P_0=\text{diag}([1e6, 1e2, 1e6, 1e2])
x0=[30000,80,20000,50]TP0=diag([1e6,1e2,1e6,1e2])
CV CT 模型的具体方程形式见另一个博客
二、测量模型:2D主动雷达
在二维情况下,雷达量测为距离和角度
r
k
m
=
r
k
+
r
~
k
b
k
m
=
b
k
+
b
~
k
{r}_k^m=r_k+\tilde{r}_k\\ b^m_k=b_k+\tilde{b}_k
rkm=rk+r~kbkm=bk+b~k
其中
r
k
=
(
x
k
−
x
0
)
+
(
y
k
−
y
0
)
2
)
b
k
=
tan
−
1
y
k
−
y
0
x
k
−
x
0
r_k=\sqrt{(x_k-x_0)^+(y_k-y_0)^2)}\\ b_k=\tan^{-1}{\frac{y_k-y_0}{x_k-x_0}}\\
rk=(xk−x0)+(yk−y0)2)bk=tan−1xk−x0yk−y0
[
x
0
,
y
0
]
[x_0,y_0]
[x0,y0]为雷达坐标。雷达量测为
z
k
=
[
r
k
,
b
k
]
′
z_k=[r_k,b_k]'
zk=[rk,bk]′。
5.2. 跟踪轨迹和误差RMSE
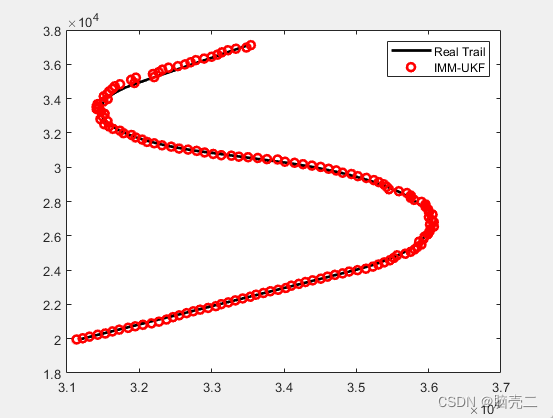
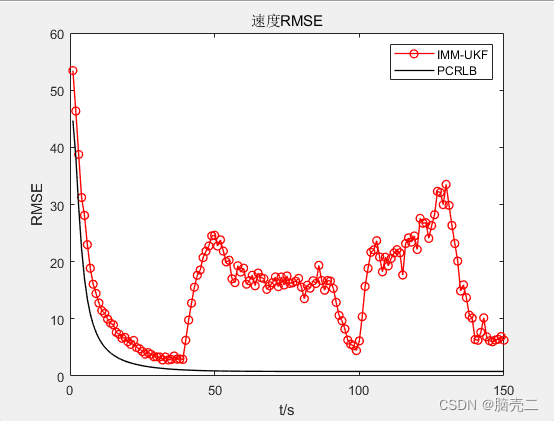
IMM模型转移概率: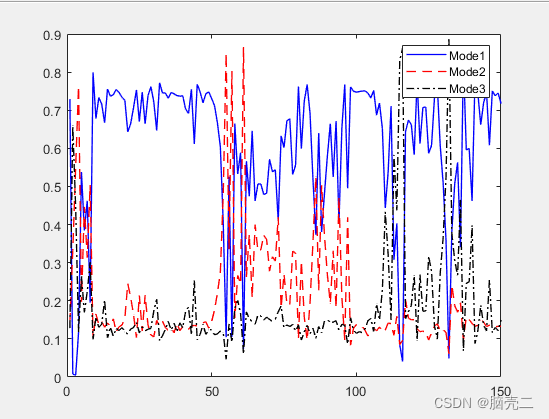
6. IMM-PF在机动目标跟踪中的应用——matlab场景二
6.1. 仿真过程
一、目标模型:CV CT CV
第一阶段:1:39s,匀速运动CV
第二阶段:40:91s,匀速圆周运动CT,角速度:
6
∗
π
/
180
;
6*\pi/180;
6∗π/180;
第三阶段:92:99s,匀速运动CV
第四阶段:100:131s,匀速圆周运动CT,角速度:
−
5
∗
π
/
180
;
-5*\pi/180;
−5∗π/180;
第五阶段:132:150s,匀速运动CV
二、测量模型:2D主动雷达
在二维情况下,雷达量测为距离和角度
6.2. 跟踪轨迹和误差RMSE
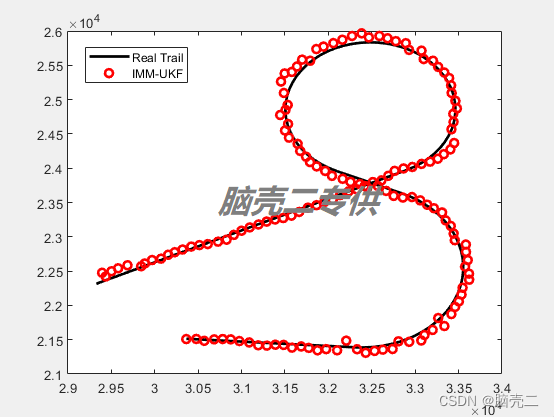

IMM模型转移概率:
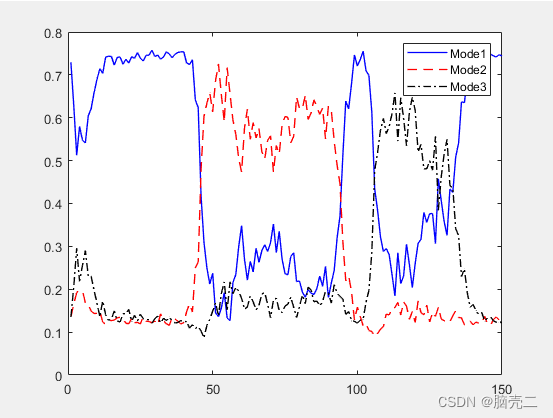
7、IMM-PF部分代码
% Interacting Multiple Model2
% created by:%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 二维目标跟踪,IMM-PF
% 目标模型:近似匀速运动模型CV 近似匀角速度运动模型CT
% 状态 x=[x位置, x速度, y位置, y速度]'
% 量测模型:三维量测(距离,角度)% 算法: 单雷达的IMM-UKF
% 性能指标:真实轨迹,RMSE均方根误差,
% 使用三个模型进行交互,分别为CV, CT, CT
close all;
clear all;
clc;%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%系统参数设置
runs=30;%蒙特卡洛实验次数,滤波将进行100次
steps=150;%每次滤波进行80次采样
%% N=1000;%粒子滤波例子点个数
%模型1的动态方程参数设置,Xk+1=fk(Xk)+G*uk+Gk*Wk,CV模型
T=1;
Fk1=[1 T 00;0100;001 T;0001;];
q1=0.1;% 目标运动学标准差,过程噪声
Qk1=q1^2*[T^3/3, T^2/2,0,0;
T^2/2, T^2,0,0;0,0, T^3/3, T^2/2;0,0, T^2/2, T^2;];% 过程噪声协方差
Gk=eye(4);%过程噪声增益矩阵
%模型2的动态方程参数设置,Xk+1=fk(Xk)+G*uk+Gk*Wk,CT模型
w1 =6*pi/180;
Fk2=[1sin(w1*T)/w1 0-(1-cos(w1*T))/w1 ;0cos(w1*T)0-sin(w1*T);0(1-cos(w1*T))/w1 1sin(w1*T)/w1 ;0sin(w1*T)0cos(w1*T);];
q2 =0.01;%% Qk2= q2^2*[2*(w1*T-sin(w1*T))/w1^3(1-cos(w1*T))/w1^20(w1*T-sin(w1*T))/w1^2;%%(1-cos(w1*T))/w1^2 T -(w1*T-sin(w1*T))/w1^20;%%0-(w1*T-sin(w1*T))/w1^22*(w1*T-sin(w1*T))/w1^3(1-cos(w1*T))/w1^2;%%(w1*T-sin(w1*T))/w1^20(1-cos(w1*T))/w1^2 T;];
Qk2=q1^2*[T^3/3, T^2/2,0,0;
T^2/2, T^2,0,0;0,0, T^3/3, T^2/2;0,0, T^2/2, T^2;];% 过程噪声协方差
%模型3的动态方程参数设置,Xk+1=fk(Xk)+G*uk+Gk*Wk,CT模型
w =-5*pi/180;
Fk3=[1sin(w*T)/w 0-(1-cos(w*T))/w ;0cos(w*T)0-sin(w*T);0(1-cos(w*T))/w 1sin(w*T)/w ;0sin(w*T)0cos(w*T);];%% Qk3= q2^2*[2*(w*T-sin(w*T))/w^3(1-cos(w*T))/w^20(w*T-sin(w*T))/w^2;%%(1-cos(w*T))/w^2 T -(w*T-sin(w*T))/w^20;%%0-(w*T-sin(w*T))/w^22*(w*T-sin(w*T))/w^3(1-cos(w*T))/w^2;%%(w*T-sin(w*T))/w^20(1-cos(w*T))/w^2 T;];
Qk3=q1^2*[T^3/3, T^2/2,0,0;
T^2/2, T^2,0,0;0,0, T^3/3, T^2/2;0,0, T^2/2, T^2;];% 过程噪声协方差
%量测方程参数设置,Zk=H*Xk+Vk
v_mu=[0,0]';% 雷达传感器标准差,即测量噪声
sigma_r=30; sigma_b=0.3*pi/180;%雷达1% 雷达坐标
xp(:,1)=[20000,0,20000,0];%第1个传感器的位置,可设置[x坐标, 0, y坐标, 0],xy对应传感器二维位置中间的0不能变,只是为了适应维数
%滤波初始化设置
X_aver_zero=[30000,80,20000,50]';
P_zero=diag([1e6,1e3,1e6,1e3]);
figure(1);for k=1:steps
% index=200;a0(:,k)=X_true(:,k,index);a1(:,k)=X_IMM(:,k,index);
end
hndl=plot(a0(1,:),a0(3,:),'k',a1(1,:),a1(3,:),'ro');set(hndl,'LineWidth',2);% 线条粗细
hold on;legend('Real Trail','IMM-UKF');
figure;
k=1:steps;
hndl=plot(k,API(1,k),'-b',k,API(2,k),'--r',k,API(3,k),'-.k');set(hndl,'LineWidth',1);% 线条粗细
legend('Mode1','Mode2','Mode3');
原创不易,路过的各位大佬请点个赞
版权归原作者 脑壳二 所有, 如有侵权,请联系我们删除。