公钥密码算法
公钥密码算法，又称非对称密码算法，使用两个密钥：
- 一个密钥是保密的，称作“私钥”
- 另一个密钥是公开的，称作“公钥” 这两个密钥存在一些特殊的数学关系：从私钥可以推导出公钥，但从公钥不能推导出私钥。
公钥密码算法一般包括加解密、签名验签两种使用模型
加解密模型：Alice想要和Bob秘密通信时，只需要用Bob的公钥对明文加密，Bob接收到密文后，用自己的私钥解密就可以得到明文了。其他人不知道Bob的私钥，所有无法解密出明文。
签名验签模型：借助数学方法可实现类似手写签名的作用，Alice使用自己的私钥对消息进行签名，然后将结果发送给Bob，Bob收到消息以后，使用Alice的公钥验证它。因为只有拥有相应私钥的用户，才能产生可验证通过的消息，所以Alice事后不能否认自己的签名。
PKI
由于攻击者可以冒充通信双方生成公私密钥对，因此，要应用公钥密码算法，首先要解决公钥归属问题。PKI通过数字证书，很好地证明了公钥是谁的。
PKI（Public Key Infrastructure），公钥基础设施，PKI是一种遵循标准的利用公钥加密技术为电子商务的开展提供一套安全基础平台的技术和规范。
通俗理解：PKI就是利用公开密钥理论和技术建立提供安全服务的、具有通用性的基础设施，是创建、颁发、管理、注销公钥证书所涉及的所有软件、硬件集合体，PKI可以用来建立不同实体间的"信任"关系，它是目前网络安全建设的基础与核心。PKI的主要任务是在开放环境中为开放性业务提供基于非对称密钥密码技术的一系列安全服务，包括身份证书和密钥管理、机密性、完整性、身份认证和数字签名等。
- PKI能够提供什么？
真实性：标识与身份鉴别——确保与你通信的另一方是它所声称的真实身份。
完整性：不被修改，没有错误——保证信息在存储或传输过程中保持不被篡改、破坏。
机密性：隐私与保密——除了通信双方之外，其他方无法获知该信息。
非否认性：责任确定——任何一方无法抵赖自己曾做过的操作。
- PKI系统组成结构 PKI基本结构由证书认证机构（certificate authority, CA）、证书持有者（certificate holder）、依赖方（relying party）三方构成：
1.CA是一个独立的可信第三方，为证书持有者签发数字证书，数字证书中声明了证书持有者的身份和公钥。CA在签发证书前应对证书持有者的身份信息进行核实验证，并根据其核验结果为其签发证书。
2.证书持有者向CA申请数字证书，并向CA提供必要的信息以证明其身份及能力，获得由CA签发的证书；证书持有者在与依赖方进行交互时，需向依赖方提供由CA签发的数字证书证明其有效身份。
3.依赖方是证书的验证方，依赖方与证书持有者进行交互（如建立通信连接）时，需获取证书持有者的数字证书，验证数字证书的真实性和有效性。依赖方可以指定其信任的CA列表，若证书持有者提供的数字证书不是受信CA签发的数字证书，依赖方将不认可该证书所声明的信息。
- 数字证书 数字证书是PKI最基本的元素，也是承载PKI安全服务最重要的载体。 证书存在的意义在于回答“公钥属于谁”的问题，以帮助用户安全地获得对方的公开密钥。 证书中最基本的内容是证书持有者的身份信息和公钥数据，以及用于验证证书完整性的CA签名结果。X.509证书是通用的PKI数字证书格式，如下图所示。
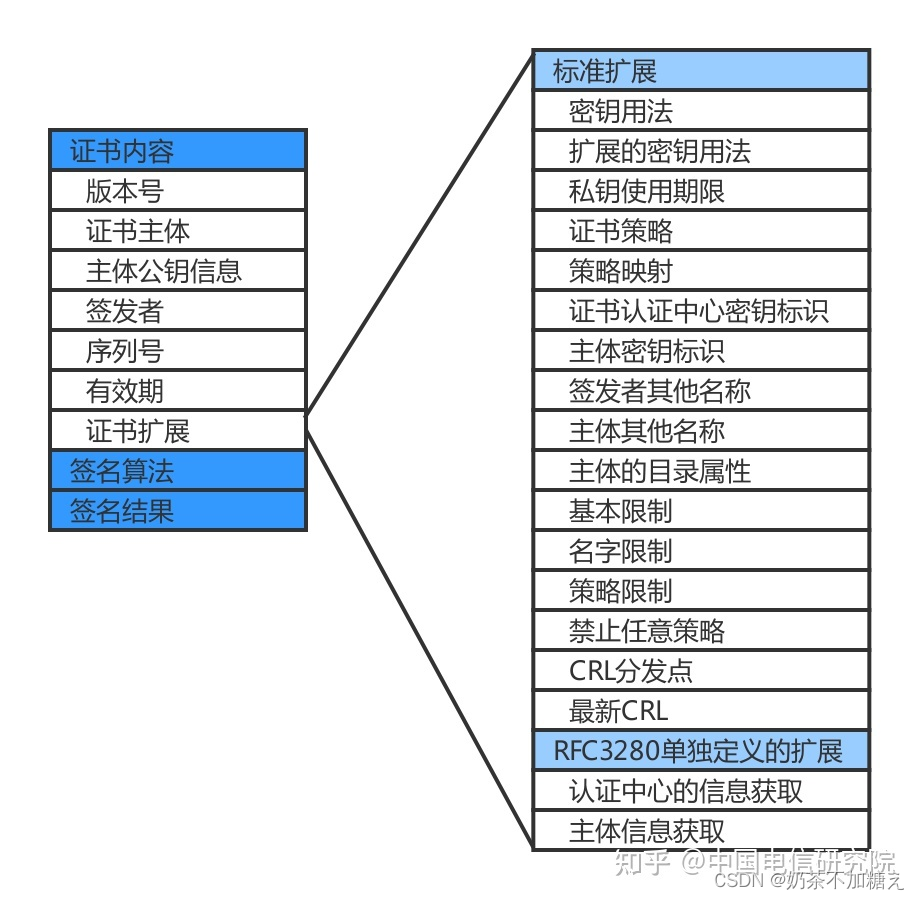一张X.509数字证书由证书内容、签名算法和签名结果组成。需要使用他人证书的用户，依照签名算法，用CA的公钥验证签名结果，从而保证证书的完整性，安全地获取公钥。 - PKI的主要应用场景 PKI提供的安全服务恰好可以满足电子商务、电子政务、网上银行、网上证券等金融业交易的安全需求，是确保这些活动顺利进行必备的安全措施，没有这些安全服务，电子商务、电子政务、网上银行、网上证券等都无法正常运作。
对称加密算法
对称加密采用了对称密码编码技术，它的特点是文件加密和解密使用相同的密钥，即加密密钥也可以用作解密密钥，这种方法在密码学中叫做对称加密算法。如DES、3DES、RC5等。
数字签名
甲向乙发送消息，乙怎么知道这个消息是不是甲发给他的？
答案是用数字签名证明其身份。
数字签名是通过散列算法，如MD5、SHA-1等算法从大块的数据中提取一个摘要。而从这个摘要中不能通过散列算法恢复出任何一点原文，即得到的摘要不会透露出任何最初明文的消息，但如果原信息受到任何改动，得到的摘要却肯定会有所不同。因此甲可以对文件进行散列算法得到摘要，并用自己的私钥加密，这样即使黑客截获也无用，黑客不会从摘要内获得任何信息，但乙不一样，他可用甲的公钥解密，得到其摘要（如果公钥能够解开此摘要，说明此摘要肯定是甲发的，因为只有甲的公钥才能解开用甲的私钥加密的信息，而甲的私钥只有甲自己知道），并对收到的文件（解密后的合同文件）也进行同样的散列算法，通过比较其摘要是否一致，就可得知此文件是否被篡改过（因为若摘要相同，则肯定信息未被改动，这是散列算法的特点）。这样不仅解决了证明发送人身份的问题，同时还解决了文件是否被篡改的问题。
KDC
KDC（Key Distribution Center），密钥分发中心，是一种运行在物理安全服务器上的服务。KDC维护着领域中（与Windows中的域相当）所有安全主体（Security Principal）账户信息数据库。
KDC是什么？
KDC和每一个节点都有一个共享密钥，每个节点希望和其它节点通信，则首先和KDC联系，由KDC分配一个临时的会话密钥。
Kerberos协议
Kerberos是一种基于对称密钥、在网络上实施身份认证的服务。包含认证服务器(AS)和门票授权服务器（TGS）。
-能够实现用户、客户端和服务器之间的互相鉴别
Kerberos协议流程
参考 https://www.freebuf.com/articles/network/265320.html
DH算法
参考 https://blog.csdn.net/u013837825/article/details/123749636
迪菲-赫尔曼密钥交换（Diffie–Hellman key exchange，缩写为D-H） 是一种安全协议。
它可以让双方在完全没有对方任何预先信息的条件下，通过不安全信道交换一个信息，创建起一个密钥。这个密钥可以在后续的通讯中作为对称密钥来加密通讯内容。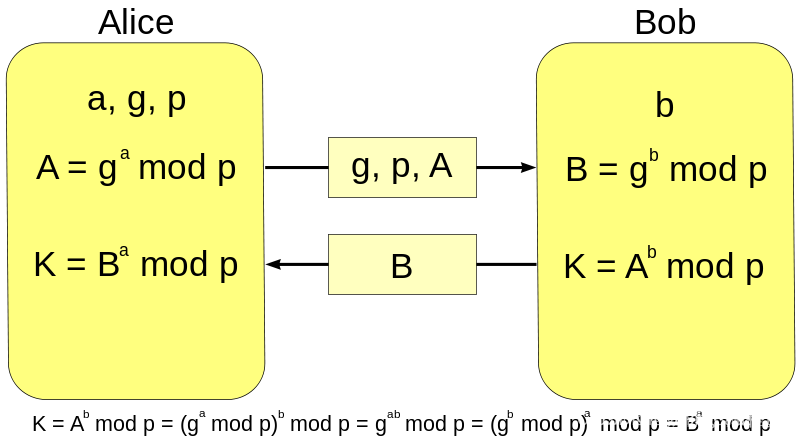
原理
最简单，最早提出的协议使用一个质数p的整数模n乘法群以及其原根g。下面展示这个算法，绿色表示非秘密信息，红色粗体表示秘密信息：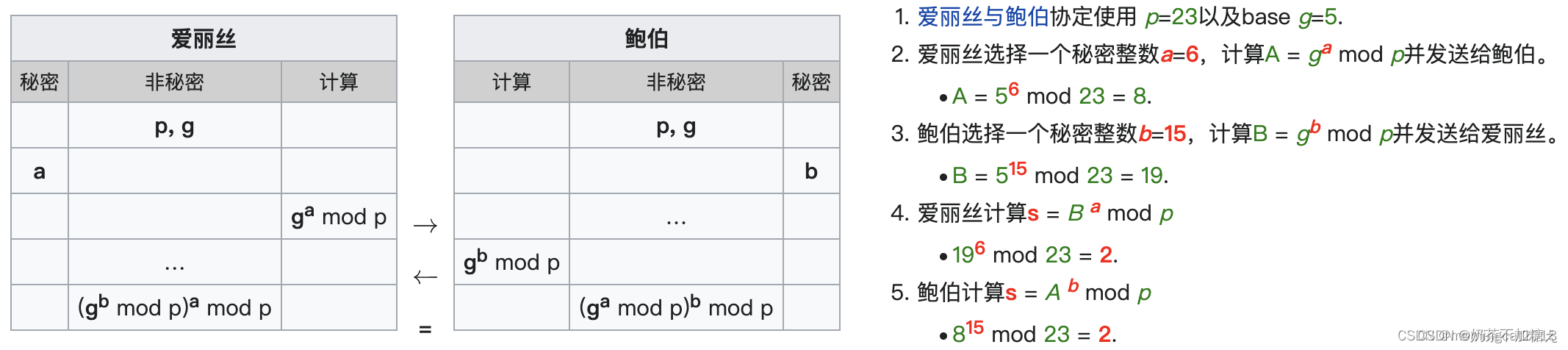
爱丽丝和鲍伯最终都得到了同样的值，因为在模p下 g^{ab} 和 g^{ba} 相等。
假设 p为素数，对于正整数 a,x,y，
有： (a^x mod p)^y mod p = a^(xy) mod p
证明如下：
令 a^x= mp + n， 其中 m, n 为自然数， 0 <= n < p，
则有 C
= (a^x mod p)^y mod p
= ((mp + n) mod p)^y mod p
= n^y mod p
= (mp +n)^y mod p
= a^(xy) mod p
这个问题就是著名的离散对数问题。注意g则不需要很大，并且在一般的实践中通常是2或者5。IETF RFC3526 文档中有几个常用的大质数可供使用。
DH算法的缺点
DH算法虽然可以保护通信信息安全，但却无法确认通信双方的真实身份，很难防范中间人的攻击。所以在日常使用中，DH算法经常辅以其他的数字签名算法（如RSA等）一同使用，用于验证通信双方的真实身份。
RSA算法
RSA算法是目前理论和实际应用中最为成熟的和完善的公钥密码体制。RSA用来解决对称密码的密钥分发问题。还可以用来进行数字签名来保证信息的否定与抵赖，利用数字签名较容易发现攻击者对信息的非法篡改以保证信息的完整性。
RSA的安全性依赖于大整数的因子分解的困难性，为了满足信息安全强度的需求，密钥的位数都比较多(521位甚至更高)，导致幂模运算的运算量极大，成为提高RSA算法加解密速度的瓶颈。
数学基础
- 素数和互素数
称整数p(p>1)是素数，如果p的因子只有±1，±p。
若满足下面2个条件，则称c是两个整数a、b的最大公因子，表示为c=gcd(a, b)。
• ① c是a的因子也是b的因子，即c是a、b的公因子。
• ② a和b的任一公因子，也是c的因子。
如果gcd(a,b)=1，则称a和b互素。
- 模运算 • 设n是一正整数，a是整数，如果用n除a，得商为q，余数为r，用a mod n表示余数r。 • 如果(a mod n)=(b mod n)，则称两整数a和b模n同余，记为a≡b mod n。 • 称与a模n同余的数的全体为a的同余类，记为[a]，称a为这个同余类的表示元素。 • 注意： 如果a≡0(mod n)，则n|a。那么就称n整除a • 同余有以下性质： • ① 若n|(a-b)，则a≡b mod n。 • ② (a mod n)=(b mod n)，则a≡b mod n。 • ③ a≡b mod n,则b≡a mod n。 • ④ a≡b mod n,b≡c mod n,则a≡c mod n。
- 费马小定理(Fermat Theory) ： • p素数，a是整数且不能被p整除，则：a^(p-1)≡ 1 mod p • 例：a = 7，p = 19，则a^(p-1) = 7 ^18 ≡ 1 （mod 19） {表示用19来除，余数是1}
- 欧拉(Euler)函数(n) • (n)表示小于n且与n互素的正整数个数。例：(6) = 2 • p是素数，§ = p－1 。例：(7) = 6 • 若gcd(m,n) = 1，则(mn) = (m)(n) • 特别地,若pq，且都是素数，(pq)=(p-1)(q-1)。如： (21) = 12 = (3)× (7) = 2×6
RSA密码体制的建立
- 产生密钥对
• 1、选择两个大素数p,q, p≠q（保密，选择）
• 2、计算n=pq，(n)=(p-1)(q-1) （公开，计算出）
• 3、选择整数e，使得gcd(e,(n))=1 （公开，选择）
• 4、计算ed 1 mod (n) （保密，计算出）
- 公钥:KU={e, n}, 私钥: KR={d, n}
- 使用 • 加密: C = M^e mod n • 解密: M = C^d mod n 尝试证明 • C = Me mod n = (Cd mod) e mod n
RSA的实例
选p = 7，q = 17，则
• n = pq = 119， (n)=(p-1)(q-1) = 6×16 = 96
取e = 5，它小于96，并且与96互为素数
• 则d = 77 ( ∵5×77 = 385 = 4×96＋1≡1 mod 96 )
公钥（5，119），私钥（77，119）
加密M = 19
• 则C = M^e mod n = 19^5 mod 119 = 66 mod 119
解密C = 66
• M = C^d mod n = 66^77mod 119 = 19 mod 119
RSA算法的优缺点
优点：
1.密钥分发简单。由于加密密钥和解密密钥不同，并且不能由加密密钥推出解密密钥，从而使得加密密钥表可以像电话号码本一样由主管部门发送给各个用户。
2.需要秘密保存的密钥量减少。
3.可以满足互不认识的人之间的私人通信的保密性要求。
4.可以完成数字签名和认证。
缺点
1.产生密钥很麻烦。受到素数产生技术的影响，很难做到一次一密。
2.安全性。
3.速度慢。
版权归原作者 奶茶不加糖え 所有， 如有侵权，请联系我们删除。