文章目录
1 交并比（Intersection over Union，IoU）
1.1 传统 IoU
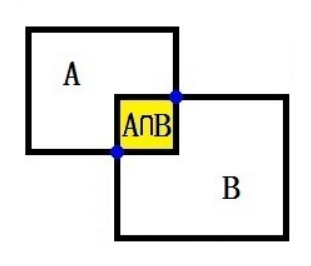
公式：
S
A
∪
B
=
S
A
+
S
B
−
S
A
∩
B
\rm S_{A\cup B}=S_{A}+S_{B}-S_{A\cap B}
SA∪B=SA+SB−SA∩B
1.2 语义分割中的IoU
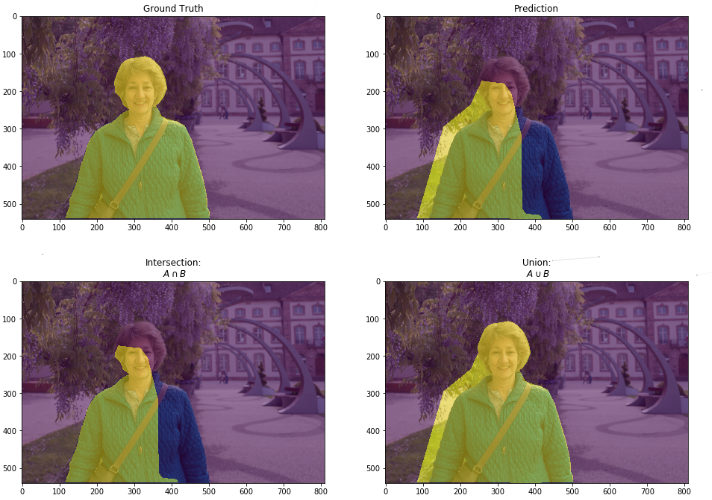
语义分割问题中的两个集合为：真实值（ground truth）和预测值（predicted segmentation）。这个比例可以变形为正真数（intersection）比上真正、假负、假正（并集）之和。在每个类上计算IoU，之后平均。
1.3 语义分割中的MIoU
均交并比（Mean Intersection over Union，MIoU）：语义分割的标准度量，计算所有类别交集和并集之比的平均值。
2 MIoU 的计算
2.1 MIoU 的计算
以pascal数据集为例，其包含 21个 类别, 分别对每个类别求
I
o
U
IoU
IoU 。令
k
k
k 表示类别
(
k
+
1
)
(k+1)
(k+1) 表示加上了背景类，
i
i
i 表示真实值，
j
j
j 表示预测值，
p
i
j
p_{ij}
pij 表示将
i
i
i 预测为
j
j
j，则某一类别的
M
I
o
U
MIoU
MIoU 可按如下方式计算：
M
I
o
U
=
1
k
+
1
∑
i
=
0
k
p
i
i
∑
i
=
0
k
p
i
j
+
∑
i
=
0
k
p
j
i
−
p
i
i
MIoU = \frac{1}{k+1}\sum_{i=0}^{k} \frac{p_{ii}}{\sum_{i=0}^{k}p_{ij}+\sum_{i=0}^{k}p_{ji}-p_{ii}}
MIoU=k+11i=0∑k∑i=0kpij+∑i=0kpji−piipii
其中，
p
i
j
p_{ij}
pij 将
i
i
i 预测为
j
j
j，为假负（FN）；
p
j
i
p_{ji}
pji 将
j
j
j 预测为
i
i
i，为假正（FP）；
p
i
i
p_{ii}
pii 将
i
i
i 预测为
i
i
i，为真正（TP）。因此，可等价于
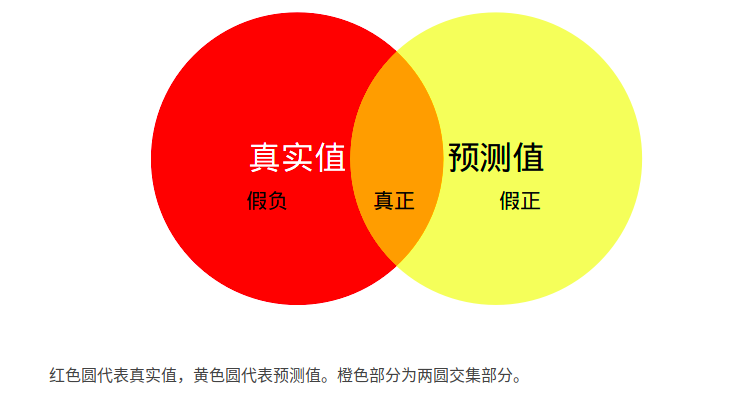
（正类：类别
i i i, 负类：非类别 i i i）TP（真正）: 预测正确, 预测结果 = 真实 = 正类 ；
FP（假正）: 预测错误, 预测结果 = 正类≠ \ne = 真实 = 负类；FN（假负）: 预测错误, 预测结果 = 负类
≠ \ne = 真实 = 正类；TN（真负）: 预测正确, 预测结果 = 负类 = 真实 = 负类；
M
I
o
U
=
1
k
+
1
∑
i
=
0
k
T
P
F
N
+
F
P
+
T
P
MIoU = \frac{1}{k+1}\sum_{i=0}^{k} \frac{TP}{FN+FP+TP}
MIoU=k+11i=0∑kFN+FP+TPTP
M
I
o
U
MIoU
MIoU ：计算两圆交集（橙色部分）与两圆并集（红色+橙色+黄色）之间的比例，理想情况下两圆重合，比例为 1。
2.2 MIoU 计算实例
步骤 1：求混淆矩阵
混淆矩阵：表示预测值和真实值之间的差距的矩阵，形式如下
[ T P （ 真 正 ） F N （ 假 负 ） F P （ 假 正 ） T N （ 真 负 ） ] \left[ \begin{array} l TP（真正）& FN（假负） \\ FP（假正） & TN（真负） \end{array} \right ] [TP（真正）FP（假正）FN（假负）TN（真负）]
步骤 2：计算 MIoU
混淆矩阵的每一行（FN+TP）再加上每一列（FP+TP），最后减去对角线上（TP）的值：
M I o U = 1 k + 1 ∑ i = 0 k 第 i 个 对 角 线 上 的 值 第 i 行 的 值 + 第 i 列 的 值 − 第 i 个 对 角 线 上 的 值 MIoU = \frac{1}{k+1}\sum_{i=0}^{k} \frac{第~i~个对角线上的值}{第~i~行的值+第~i~列的值-第~i~个对角线上的值} MIoU=k+11i=0∑k第 i 行的值+第 i 列的值−第 i 个对角线上的值第 i 个对角线上的值
计算 MIoU 例子源码
【参考】
- 语义分割代码阅读—评价指标mIoU的计算；
- 语义分割指标计算之miou（交并比）；
- 混淆矩阵是什么意思？
标签：
MIoU
本文转载自: https://blog.csdn.net/qq_41731861/article/details/120683905
版权归原作者 晓野豬 所有， 如有侵权，请联系我们删除。
版权归原作者 晓野豬 所有， 如有侵权，请联系我们删除。