【初识java】递归的应用+详解经典汉诺塔+详解青蛙跳台阶

大家好我是枫晨，前面一文中对java中的方法进行了学习，学习方法必然少不了对递归的学习，另外欢迎阅读我的其他文章:
🖌️作者主页:XY枫晨
📚java专栏:java语言学习专栏

这篇文章的目标有3个:
·学会递归
·使用递归实现对汉诺塔问题的解决
·使用递归解决青蛙跳台阶的问题

文章目录

一、递归

1.1递归的定义

定义：一个方法在执行过程中在内部自己调用自己，并且有一个趋近于终止的条件，则称其是递归。(趋近于终止这个条件很重要)

递归相当于数学上的 “数学归纳法”, 有一个起始条件, 然后有一个递推公式.

例如求一个数的阶乘N!
起始条件：我们认为N=1时，N!为1，数学上的起始条件在递归中其实就是递归的终止条件。
递归公式：我们可以定义*N=N(N-1)!**，这就是递归公式。

递归的难点就在于找到一个问题的起始条件（终止条件）和合适的递归公式。

递归代码示例:求N的阶乘

publicstaticintfactor(int n){//起始条件(终止条件)if(n ==1){return1;}else{//递归公式return n*factor(n-1);//factor调用自身}}publicstaticvoidmain(String[] args){int n =5;System.out.println(fact(n));}//==>120

1.2递归过程分析

要想理解清楚递归，就要理解方法的执行过程，下面一张图来详解一下递归的整个过程。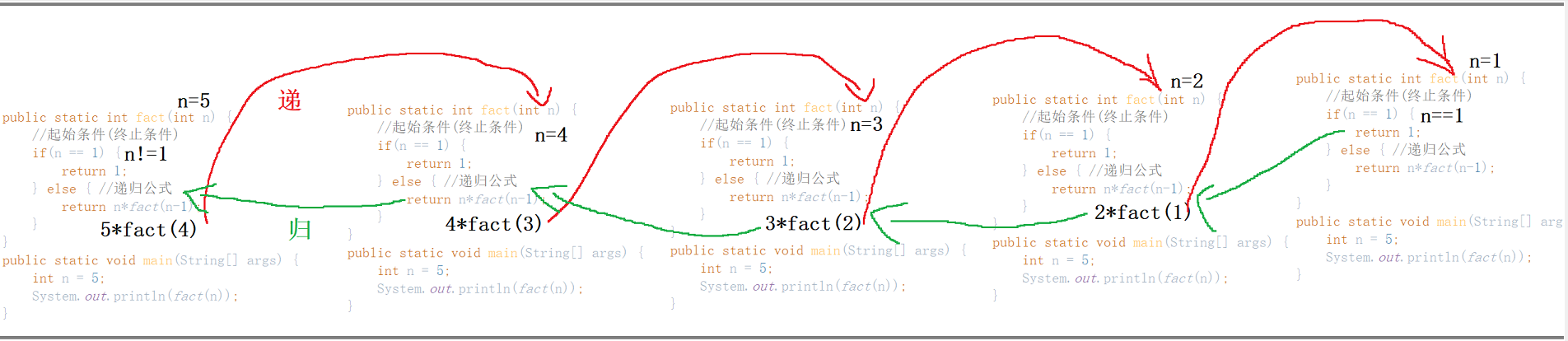

值得一提的是，递归必须有一个结束条件，否则的话，栈上会不断为调佣的方法开辟栈帧空间，导致内存溢出问题

1…3递归练习

练习1:按顺序打印数字的每一位(如456打印出 4 5 6)

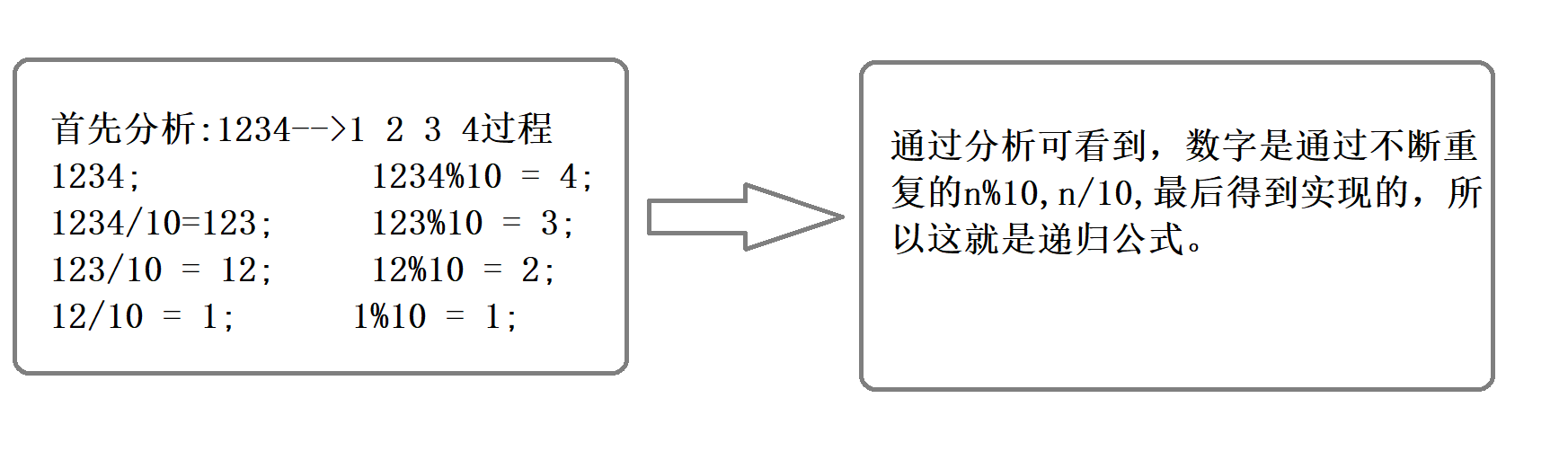
publicstaticvoidprint(int n){if(n>=10){print(n/10);}System.out.println(n%10);}

练习2:输入一个非负整数，返回组成它的数字之和. 例如，输入 1729, 则应该返回1+7+2+9，它的和是19；

publicstaticintsum(int n){if(n<=9){return n;}else{return n%10+sum(n/10);}}

练习3：求斐波那契数列的第n项

publicstaticintfib(int n){if(n==1||n==2){return1;}else{returnfib(n-1)+fib(n-2);//前两项之和}}

但是在实际开发过程中如果有需求运用到斐波那契数列，并不推荐使用递归方式，使用递归求取斐波那契数列会出现重复计算的问题，一般都是利用迭代的方式来解决斐波那契数列问题。

二、汉诺塔问题的详解

汉诺塔（Tower of Hanoi），又称河内塔，是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。—百度百科

如果单独看这个，我第一次看到时候是一脸懵逼的，其实当我们利用图像来理解时候，这个问题就会清晰很多。

64个盘子情况我们暂且先不讨论，先以3个盘子的情况入手，通过上图我们可以构造一个数学模型。

汉诺塔问题就是将A柱上的盘子，通过ABC柱最后按照从小到大的顺序移动到C柱上。
假设A柱上只有1个盘子，则如下图>：

则直接将盘子从A柱移动到C柱即可，我们过程记为:

A -> C; //代表从盘子从A柱移动到了C柱

假设A柱上有2个盘子，则如下图

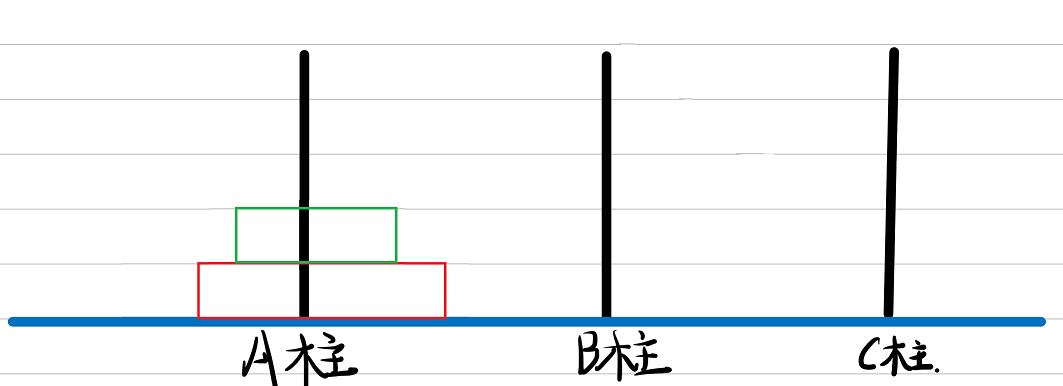
移动过程动图：

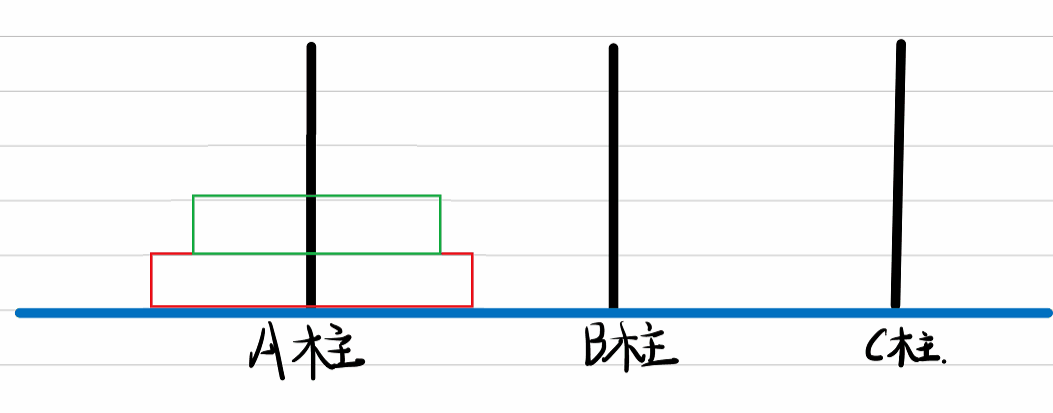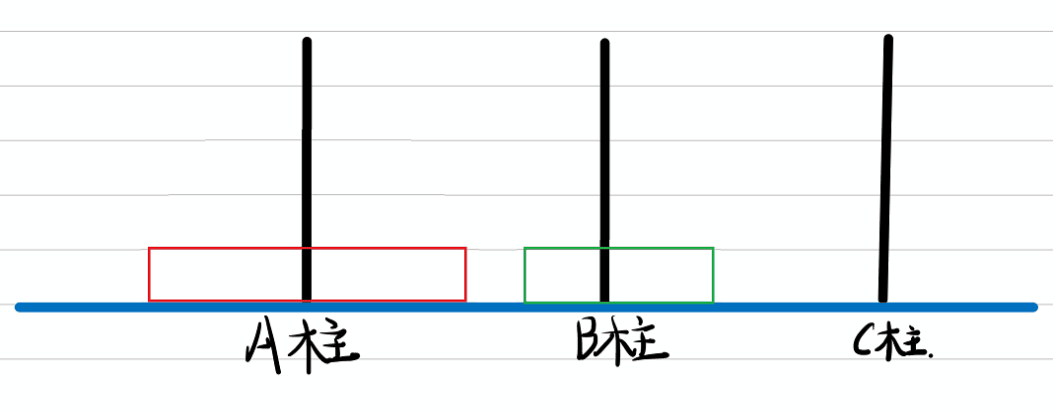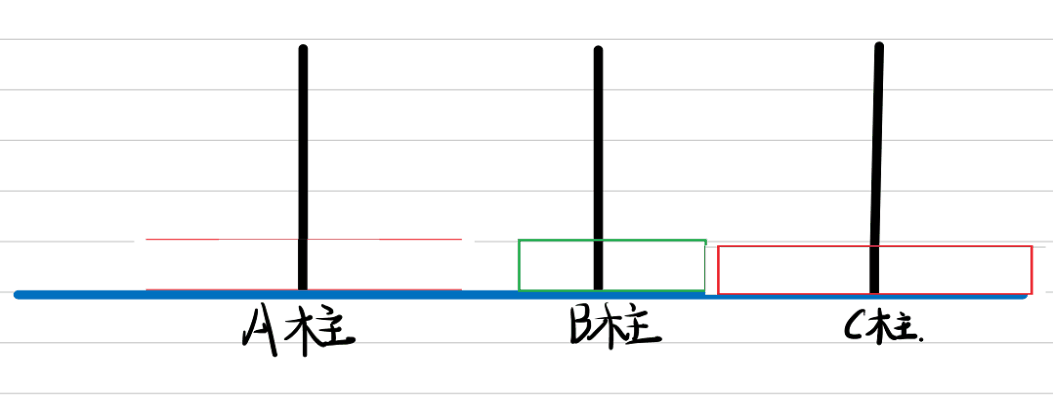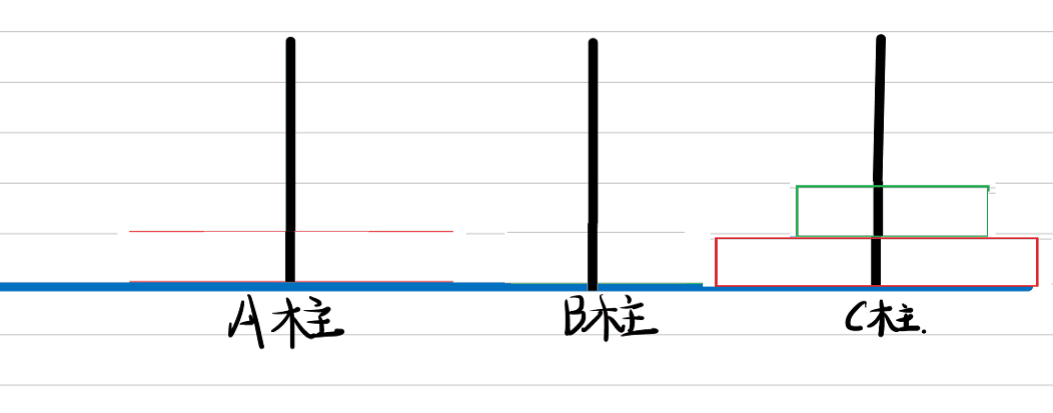
则将盘子从A柱移动到C柱的过程我们记为:

A -> B A->C B -> C

//代表先将A柱上的盘子从A柱移动到B柱，再将A柱上的盘子移动到C柱，最后再将B柱上的盘子移动到C柱

最后再来看看刚刚提到的3个盘子情况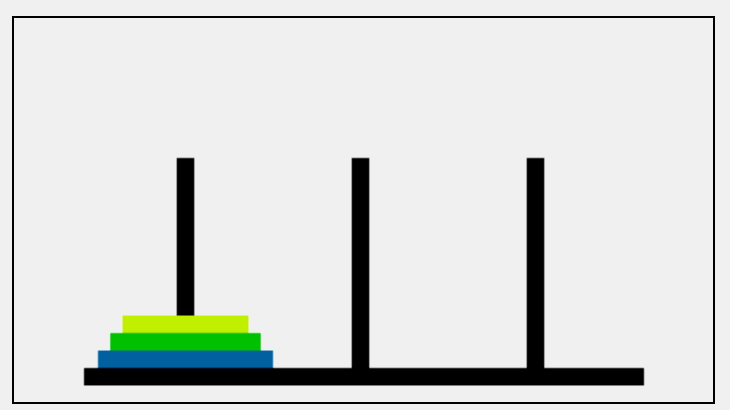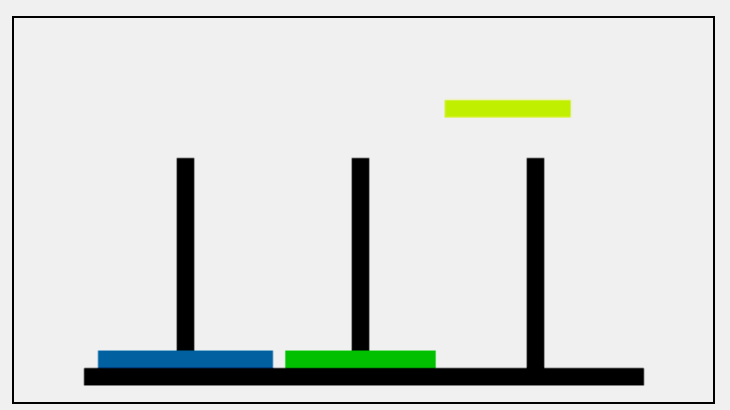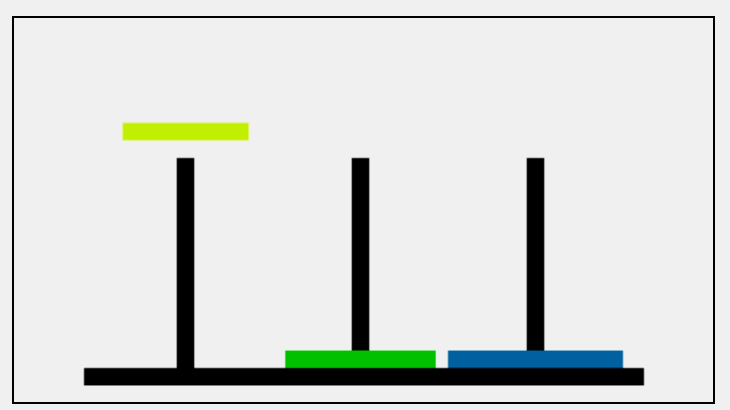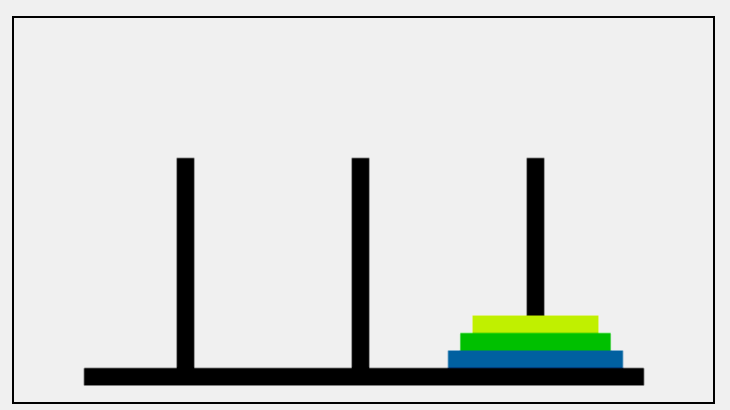

将盘子从A柱移动到C柱的过程我们记为:

A ->C A->B C->B A->C B->A B->C A->C

分析刚刚三种情况的记录：
一：A -> C —2^1-1=1次

二：A -> B A->C B -> C -----2^2-1=3次

三：A ->C A->B C->B A->C B->A B->C A->C -------2^2-1=4次

这也是为什么我们不讨论64个盘子的情况，试想2^64-1次，这得是多少年才可以移动完！

但是我们的着重点在于如何通过递归的方式解决汉诺塔的问题，通过递归找到移动盘子的最终方式。

思路：我们可以粗糙的理解，汉诺塔问题的难点在于如何将A柱下最下面的那个盘子移动去C柱上，解决这个问题之前我们要先解决剩余的(N-1)个盘子，假设最终这(N-1)个盘子全部从A柱上通过C柱移动到B柱上，此时A柱下最大的盘子可以移动到C柱上，再将B柱上的盘子通过A柱移动到C柱上

递推公式：将(N-1)个盘子放到B柱上

终止条件:N为1时，将A柱上的盘子直接移动到C柱上。

代码实现:

模块1：模拟鼠标移动

/**
     * move:模拟鼠标移动的一次过程
     * pos1位置移动到pos2位置，打印出来，相当于A -> C
     * @param pos1
     * @param pos2
     */publicstaticvoidmove(char pos1,char pos2){System.out.print(pos1+" -> "+pos2+" ");}

模块2:汉诺塔递归的实现

/**
     * @param n 代表盘子个数
     * @param pos1 A柱
     * @param pos2 B柱
     * @param pos3 C柱
     */publicstaticvoidhanoi(int n,char pos1,char pos2,char pos3){//n==1时为终止条件，直接将A柱上的盘子移动到C柱即可if(n==1){move(pos1,pos3);//pos1为起始位置，pos3为目的地位置}else{hanoi((n-1),pos1,pos3,pos2);//pos1(A)为起始位置，pos3(C)为中途位置，pos2(B)为目的地位置。含义：将n-1个盘子从A柱上通过C柱移动到B柱上(递推公式)move(pos1,pos3);//pos1为起始位置，pos3为目的地位置.将n-1个盘子移动走后，将A柱上最后的盘子移动到C柱上hanoi((n-1),pos2,pos1,pos3);//pos2(B)为起始位置，pos1(A)为中途位置，pos2CB)为目的地位置。将B柱上n-1个盘子，从B柱上通过A柱移动到C柱上}}publicstaticvoidmain(String[] args){hanoi(3,'A','B','C');//给pos1,pos2,pos3指定是哪一个柱子}

最后通过代码实现的答案与我们分析的答案是一致的！不要试图去展开递归的代码！！！思考递归的代码我们要横向思考，递归最重要的就是分析出递归公式和递归的终止条件！

三、青蛙跳台阶

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法（先后次序不同算不同的结果）

当台阶为1级时，有一种跳法，当台阶为2时，有两种跳法，分别是一次跳一级台阶，总共需要跳2次和一次跳2级，总共跳一次。

当台阶为3级时候呢？可以第一次跳1级，总共跳3次，和第一次跳一级，最后跳2级，总共跳2次，以及第一次跳2级，最后跳一级，总共跳2次，共3种方法(题目中有说先后次序不同算不同的结果)
我们不难发现，跳3级台阶时候是跳一级台阶的跳法种类加上跳二级台阶时候的跳法种类共3次。

那我们得到递推公式应该为:N=jump(N-1)+jump(N-2)
递推终止条件为N=1或N=2

则这个问题转换成代码就是:

publicstaticintjump(int n){if(n==1){return1;}elseif(n==2){return2;}else{returnjump(n-1)+jump(n-2);}}

递推的有关知识以及一些比较经典的题目就介绍完啦，接下来迎接我们的就是数组了！大家继续奋斗加油！