数据结构与算法--动态规划1

代码随想录day38 动态规划模块

文章目录

一.动态规划理论

1.1动态规划理论基础

动态规划(Dynamic Programming，简称DP)  的一般问题就是求最值，求解动态规划的核心问题是穷举，既然要找到最值，就把所有情况列举出来，但是呢动态规划不是暴力穷举，你需要优化穷举。
所有的动态规划问题都是由上一个状态来推导下一个状态，这跟贪心算法不一样，贪心是根据局部最优推出全局最优，贪心没有状态推导。

1.2动态规划做题步骤

动态规划的做题步骤

1. 确定dp数组以及下标的含义
2. 确定递推公式
3. dp数组的初始化问题
4. 遍历顺序
5. 举例推导dp公式

二.leetcode 509.斐波那契数

力扣题目链接

思路：直接根据做题步骤来：

1.确定dp数组以及下标的含义

第i个数的值就是dp[i]

2. 确定递推公式

这题递推公式已经给出来了dp[i]=dp[i-1]+dp[i-2]

3. dp数组的初始化问题

dp[0]=0,dp[1]=1;

4.确定遍历顺序

这题很明显的从前往后面遍历

5. 举例推导dp公式

当n为10的时候 dp数组为 0 1 1 2 3 5 8 13 21 34 55

然后总体的代码是

classSolution{publicintfib(int n){if(n <=1)return n;int[] dp =newint[n +1];
        dp[0]=0;
        dp[1]=1;for(int i=2; i <= n; i++){
            dp[i]= dp[i -1]+ dp[i -2];}return dp[n];}}

三.leetcode 70.爬楼梯

力扣题目链接

思路：直接根据做题步骤来：

1.确定dp数组以及下标的含义

爬到第i层楼梯有dp[i]种方法

2. 确定递推公式(这题的推导公式和上题是一样的)

这题递推公式已经给出来了dp[i]=dp[i-1]+dp[i-2]

3. dp数组的初始化问题

dp[0]=1,dp[1]=1;

4.确定遍历顺序

这题很明显的从前往后面遍历

5. 举例推导dp公式

当n=5时，dp数组 1 2 3 5 8

详细代码

classSolution{publicintclimbStairs(int n){if(n<2)return n;int[] arr=newint[n+1];
     arr[0]=1;
     arr[1]=1;for(int i=2;i<arr.length;i++){
      arr[i]=arr[i-1]+arr[i-2];}return arr[n];}}

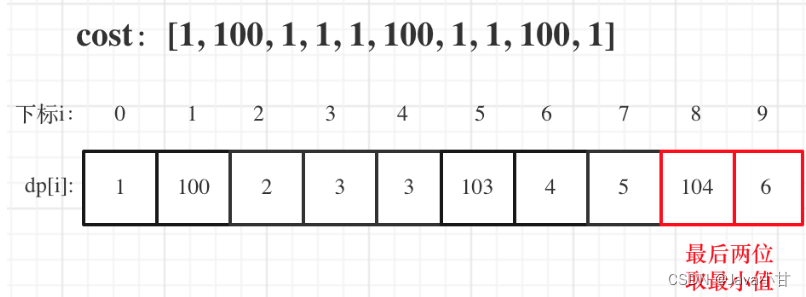
四.leetcode 746.使用最小花费爬楼梯

力扣题目链接

思路：直接根据做题步骤来：

1.确定dp数组以及下标的含义

爬到第i个位置所需要的总花费就是dp[i]

2. 确定递推公式(第一步支付费用，最后一步不支付)

dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);

3. dp数组的初始化问题

dp[0]=0,dp[1]=0;

4.确定遍历顺序

这题很明显的从前往后面遍历

5. 举例推导dp公式

详细代码

classSolution{publicintminCostClimbingStairs(int[] cost){int[] dp=newint[cost.length+1];// 从下标为 0 或下标为 1 的台阶开始，因此支付费用为0
     dp[0]=0;
     dp[1]=0;for(int i=2;i<dp.length;i++){
         dp[i]=Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}return dp[cost.length];}}