前言
从今天开始,我跟大家一起刷力扣上的练习题,先从二叉树开始,这里练好,后面的回溯算法,动态规划啥的也就得心应手了.
参考此公众号做的笔记:东哥带你刷二叉树(纲领篇) :: labuladong的算法小抄 (gitee.io)
代码随想录 (programmercarl.com)
这里面对二叉树做了详细的讲解,推荐大家去看下,我就光分享一下我做题的思路吧。
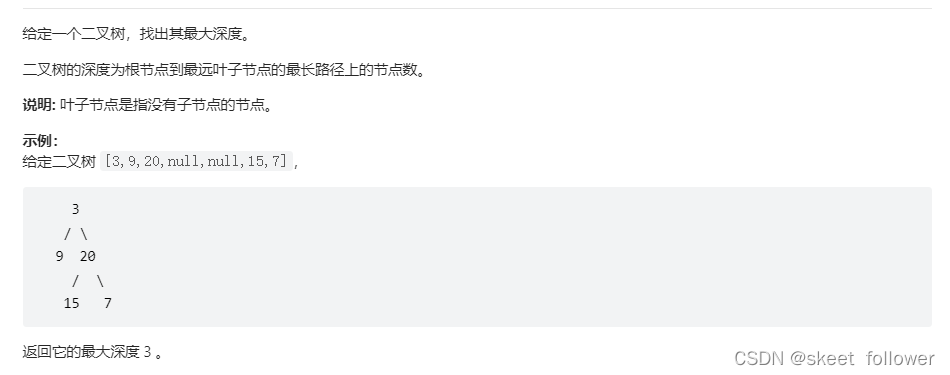
二叉树的最大深度
二叉树题目的递归解法可以分两类思路,第一类是遍历一遍二叉树得出答案,第二类是通过分解问题计算出答案,这两类思路分别对应着 回溯算法核心框架 和 动态规划核心框架。
当时我是用二叉树的最大深度这个问题来举例,重点在于把这两种思路和动态规划和回溯算法进行对比,而本文的重点在于分析这两种思路如何解决二叉树的题目。
回溯算法思路
class Solution {
public:
int res=0;//记录最大深度
int depth=0;//记录遍历到的节点深度
void travel(TreeNode* root)
{
if(root==nullptr)
{
return;
}
//前序遍历位置
depth++;//深度加1
res=max(res,depth);//更新最大深度
travel(root->left);//左
travel(root->right);//右
depth--;//回溯,深度-1
//后序遍历位置
}
int maxDepth(TreeNode* root) {
travel(root);
return res;
}
};
这道题为什么在前序遍历位置depth++,在后序遍历位置depth--囊?其实很简单,就是前序遍历是进入一个节点位置的时候,后序遍历是离开一个结点的时候,depth是记录当前遍历到的节点的深度,你把travel理解成一个在二叉树上游走的指针,当然要进行这样的维护。
动态规划思想
class Solution {
public:
int maxDepth(TreeNode* root) {
if(root==nullptr)
{
return 0;
}
// 利用定义,计算左右子树的最大深度
int left=maxDepth(root->left);
int right=maxDepth(root->right);
// 整棵树的最大深度等于左右子树的最大深度取最大值,
// 然后再加上根节点自己
return max(left,right)+1;
}
};
只要明确递归函数的定义,这个解法也不难理解,但为什么主要的代码逻辑集中在后序位置?
因为这个思路正确的核心在于,你确实可以通过子树的最大高度推导出原树的高度,所以当然要首先利用递归函数的定义算出左右子树的最大深度,然后推出原树的最大深度,主要逻辑自然放在后序位置。
广度优先搜索
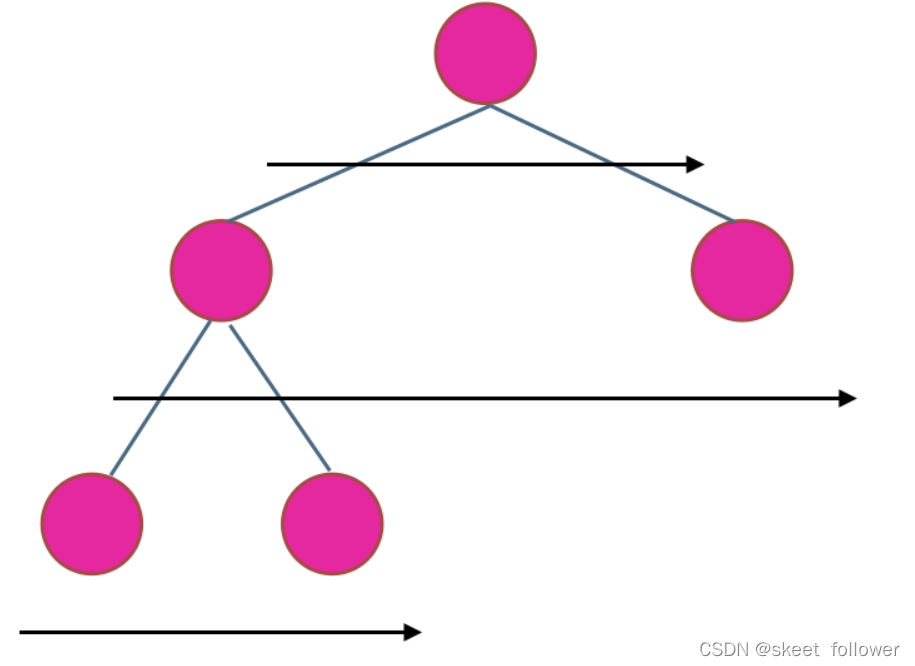
使用层序遍历是最为合适的,因为最大的深度就是二叉树的层数,和层序遍历的方式极其吻合。
在二叉树中,一层一层的来遍历二叉树,记录一下遍历的层数就是二叉树的深度,如图所示:
class Solution {
public:
int maxDepth(TreeNode* root) {
if(root==nullptr)
{
return 0;
}
queue<TreeNode*> res;
res.push(root);
int ants=0;
while(!res.empty())
{
int sz=res.size();
for(int i=0;i<sz;i++)
{
TreeNode* node=res.front();
res.pop();
if(node->left) res.push(node->left);
if(node->right)res.push(node->right);
}
ants++;
}
return ants;
}
};
N叉树的最大深度
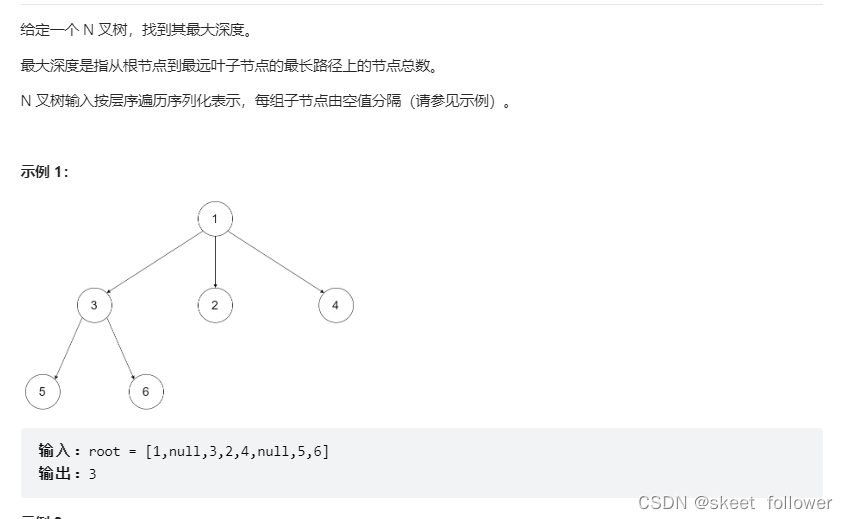
依然可以提供递归法和迭代法,来解决这个问题,思路是和二叉树思路一样的,直接给出代码如下:
递归
class Solution {
public:
int maxDepth(Node* root) {
if(root==nullptr)
{
return 0;
}
int depth=0;
for(int i=0;i<root->children.size();i++)
{
depth=max(depth,maxDepth(root->children[i]));
}
return depth+1;
}
};
迭代
class solution {
public:
int maxdepth(node* root) {
queue<node*> que;
if (root != NULL) que.push(root);
int depth = 0;
while (!que.empty()) {
int size = que.size();
depth++; // 记录深度
for (int i = 0; i < size; i++) {
node* node = que.front();
que.pop();
for (int j = 0; j < node->children.size(); j++) {
if (node->children[j]) que.push(node->children[j]);
}
}
}
return depth;
}
};

版权归原作者 skeet follower 所有, 如有侵权,请联系我们删除。