【AI底层逻辑】——“数学华尔兹”之一元线性回归

一元线性回归模型想必大家都耳熟能详，这里不再赘述。但在使用python中机器学习包时一定见过类似模型评价参数的输出，这一章我们就讲一讲回归分析里一些模型评价概念！

一、方差分析ANOVA

方差分析是一种用于确定线性回归模型中不同变量对目标变量解释程度的统计技术。方差分
析通过比较模型中不同的变量的平均方差，来确定哪些变量对目标变量的解释程度更高。如下是标准的ANOVA表格：

①Source为计算方差的三个来源。regressor回归、residuals残差、total总离。
②df代表自由度 (degrees of freedom)；自由度是指在计算统计量时可以随意变化的独立数据点
的数量。总离差自由度 DFT、回归自由度 DFR、残差自由度 DFE。
③SS代表平方和 (Sum of Squares)；平方和通常用于描述数据的变异程度，即它们偏离平均值
的程度。三个平方和SSR、SSE、SST如下。
④MS代表均方和 (Mean Sum of Squares)；在统计学中，均方和是一种平均值的度量，其计算
方法是将平方和除以自由度。
⑤F代表 F-test统计量。F检验是一种基于方差比较的统计检验方法，用于确定两个或多个样
本之间是否存在显著性差异。

⑥Significance代表显著度：F-test的p值。

1、平方和：SST、SSE、SSR

①总离差平方和 (Sum of Squares for Total, SST)，也称 TSS (total sum of squares)。SST描述所有实际值与总体均值之间差异的平方和，用来评整个数据集的离散程度。

$\text{SST}=\sum_{i=1}^n\Bigl(y^{(i)}-\overline{y}\Bigr)^2$
②残差平方和 (Sum of Squares for Error, SSE)，也称 RSS (residual sum of squares)。SSE反映了因变量中无法通过自变量预测的部分，也称为误差项（实际值与预测值之间差异的平方和），可以用于检查回归模型的拟合程度和判断是否存在异常值。在回归分析中，常通过最小化残差平方和来确定最佳的回归系数。

$\mathrm{SSE}=\sum_{i=1}^n\Bigl(y^{(i)}-\hat{y}^{(i)}\Bigr)^2$
③回归平方和 (Sum of Squares for Regression, SSR)，也称 ESS (explained sum of squares)。SSR反映了回归模型所解释的数据变异量的大小（预测值与总体均值之间差异的平方和），用于评估回归模型的拟合程度以及自变量对因变量的影响程度。

$\mathrm{SSR}=\sum_{i=1}^n\left(\hat{y}^{(i)}-\overline{y}\right)^2$

三者关系 $SST=SSR+SSE$ ，线性回归方差分析的本质是将SST分解为SSE和SSR！可发现这种关系可看作三角形勾股定理：

$\begin{aligned} &\text{SST}=\sum_{i=1}^{n}\left(y^{(i)}-\overline{y}\right)^{2}=\left\|y-\overline{y}\right\|_{2}^{2} \\ &\text{SSR}=\sum_{i=1}^{n}\left({\hat{y}}^{(i)}-{\overline{y}}\right)^{2}=\left\|{\hat{y}}-{\overline{y}}\right\|_{2}^{2} \\ &\text{SSE}=\sum_{i=1}^{n}\left(y^{(i)}-\hat{y}^{(i)}\right)^{2}=\left\|y-\hat{y}\right\|_{2}^{2} \\ &\underbrace{\left\|\boldsymbol{y}-\overline{\boldsymbol{y}}\boldsymbol{I}\right\|_{2}^{2}}_{\mathrm{ssr}}=\underbrace{\left\|\hat{\boldsymbol{y}}-\overline{\boldsymbol{y}}\boldsymbol{I}\right\|_{2}^{2}}_{\mathrm{ssR}}+\underbrace{\left\|\boldsymbol{y}-\hat{\boldsymbol{y}}\right\|_{2}^{2}}_{\mathrm{ssE}} \end{aligned}$

即： $\left(\sqrt{\mathrm{SST}}\right)^2=\left(\sqrt{\mathrm{SSR}}\right)^2+\left(\sqrt{\mathrm{SSE}}\right)^2$ 先理解下图后续会进一步分析！

2、自由度DF

自由度(degree of freedom）上面的ANOVA表格里的第2列：总离差自由度 DFT(degree of freedom total）、回归自由度 DFR(degree of freedom regression）、残差自由度 DFE(degree of freedom error）三者关系为：

$\mathrm{DFT}=n-1=\mathrm{DFR}+\mathrm{DFE}=\underbrace{\left(k-1\right)}_{\mathrm{DFR}}+\underbrace{\left(n-k\right)}_{\mathrm{DFE}}=\left(D\right)+\underbrace{\left(n-D-1\right)}_{\mathrm{DFR}}$

n代表参与回归的非 NaN样本数量。k代表回归模型参数数量，包括截距项。D代表自变量的数量（解释变量个数），因此 k = D + 1 (+1 代表常数项参数)。举个例子，对于一元线性回归，D = 1，k = 2。如果参与建模的样本数据为 n = 252，几个自由度分别为：

$\left.\left\{\begin{aligned}\mathrm{DFT}&=252-1=251\\k&=D+1=2\\\mathrm{DFR}&=k-1=D=1\\\mathrm{DFE}&=n-k=n-D-1=252-2=250\end{aligned}\right.\right.$

3、MST、MSR、MSE、RMSE

①平均总离差 (mean square total, MST) 的定义如下，实际上就是样本因变量y的方差！

$\mathrm{MST}=\mathrm{var}\big(Y\big)=\frac{\sum_{i=1}^{n}\big(y_{i}-\overline{y}\big)^{2}}{n-1}=\frac{\mathrm{SST}}{\mathrm{DFT}}$

②平均回归平方 (mean square regression, MSR) 为：

$\mathrm{MSR}={\frac{SSR}{DFR}}={\frac{SSR}{k-1}}={\frac{SSR}{D}}$

③残差平均值 (mean squared error, MSE) 为：

$\mathrm{MSE}={\frac{SSE}{DFE}}={\frac{SSE}{n-k}}={\frac{SSE}{n-D-1}}$

均方根残差 (Root mean square error, RMSE) 为 MSE的平方根：

$\mathrm{RMSE}=\sqrt{\mathrm{MSE}}=\sqrt{\frac{SSE}{DFE}}=\sqrt{\frac{SSE}{n-p}}=\sqrt{\frac{SSE}{n-D-1}}$

二、拟合优度

在回归模型创建之后，很自然就要考虑这个模型是否能够很好地解释数据，即考察这条回归线对观
察值的拟合程度，也就是所谓的拟合优度 (goodness of fit)。形象地，上面说到三个平方和之间类似勾股定理的关系时的四面体，θ越小，其对边（误差）越小，拟合优度越好。

1、决定系数

决定系数 (coefficient of determination，R2) 是定量化反映拟合优度的统计量。R2越接近1，拟合优度越好；R2越接近0，拟合优度越差。

从几何角度来看，R2是图 12中 θ余弦值 cosθ的平方：

$R^{2}=\cos(\theta)^{2}$

利用上面的勾股定理三角形可得：

$R^{2}=\frac{\mathrm{SSR}}{\mathrm{SST}}=1-\frac{\mathrm{SSE}}{\mathrm{SST}}$

特别地，对于一元线性回归，决定系数是因变量与自变量的相关系数的平方，与模型斜率项系数 b1也有直接关系。

$R^{2}=\rho_{X,Y}^{2}=\left(b_{1}\frac{\sigma_{X}}{\sigma_{Y}}\right)^{2}$

其中 $b_{1}=\rho_{x,x}\frac{\sigma_{y}}{\sigma_{x}}$

因此，线性相关系数 ρ和决定系数 R2都是衡量变量之间线性关系强弱的重要指标，可以帮助我们理解自变量对因变量的解释能力，评估模型的拟合优度，以选择最佳的回归模型。

2、修正决定系数

但仅仅使用决定系数 R2是不够的。对于多元线性模型，不断增加解释变量个数D时，R2将不断增大。我们可以利用修正决定系数 (adjusted R squared)。

$\begin{aligned} R_{\mathrm{adj}}^{2}& =1-\frac{\mathrm{MSE}}{\mathrm{MST}} \\ &=1-\frac{\mathrm{SSE}/(n-k)}{\mathrm{SST}/(n-1)} \\ &=1-\biggl(\frac{n-1}{n-k}\biggr)\frac{\mathrm{SSE}}{\mathrm{SST}} \\ &=1-\biggl(\frac{n-1}{n-k}\biggr)\biggl(1-R^{2}\biggr) \\ &=1-\biggl(\frac{n-1}{n-D-1}\biggr)\frac{\mathrm{SSE}}{\mathrm{SST}} \end{aligned}$

当模型中自变量的数量D增加时，它能够惩罚过拟合，避免了当自变量数量增加时决定系数的人为提高。过拟合通常发生在模型复杂度过高或者训练数据太少的情况下，为了避免过拟合，可以采取以下方法：增加训练数据量、降低模型复杂度、采用正则化(regularization) 技术等。

三、F检验：模型参数不全为0

在线性回归中，F检验用于检验线性回归模型参数是否显著，它通过比较回归平方和和残差平方和的大小来判断模型是否具有显著的解释能力。

1、统计量

F检验的统计量如下：

$\begin{aligned}F&=\frac{\mathrm{MSR}}{\mathrm{MSE}}=\frac{\frac{\mathrm{SSR}}{k-1}}{\frac{\mathrm{SSE}}{n-k}}=\frac{\mathrm{SSR}\left(n-k\right)}{\mathrm{SSE}\left(k-1\right)}\\&=\frac{\frac{\mathrm{SSR}}{D}}{\frac{\mathrm{SSE}}{n-D-1}}=\frac{\mathrm{SSR}\cdot\left(n-D-1\right)}{\mathrm{SSE}\cdot\left(D\right)}\rightarrow F\left(k-1,n-k\right)\end{aligned}$

2、假设检验

假设检验 (hypothesis testing) 是统计学中常用的一种方法，用于根据样本数据推断总体参数是否符合某种假设。
假设检验通常包括两个假设：原假设和备择假设。
原假设 (null hypothesis) 是指在实验或调查中假设成立的一个假设，通常认为其成立。
备择假设 (alternative hypothesis) 是指当原假设不成立时，我们希望成立的另一个假设。

通过收集样本数据，并根据统计学原理计算出样本统计量的概率分布，我们可以计算出拒绝原假设
的概率。如果这个概率小于预设的显著性水平 (比如 0.05)，就可以拒绝原假设，认为备择假设成立。反之，如果这个概率大于预设的显著性水平，就不能拒绝原假设。

F检验是单尾检验，原假设H0、备择假设H1分别为：

$\begin{aligned}H_0:&b_1=b_2=\cdots=b_D=0\\H_1:&b_j\neq0\text{ for at least one}j\end{aligned}$

具体来说，F检验的零假设（原假设）是模型的所有回归系数都等于零，即自变量对因变量没有显著的影响。
如果 F检验的 p值小于设定的显著性水平，就可以拒绝零假设，认为模型是显著的，即自变量对因变量有显著的影响。

3、临界值

临界值 Fα可根据两个自由度 (k − 1和 n − k) 以及显著性水平α查表获得。1 − α 为置信度或置信水平，通常取 α = 0.05或 α = 0.01。这表明，当作出接受原假设的决定时，其正确的可能性为 95%或 99%。

根据统计量公式计算得到的 F值和临界值 Fα进行比较，如果下式成立：

$F>F_{1-\alpha}\left(k-1,n-k\right)$

则在该置信水平上拒绝零假设H0，不认为自变量系数同时具备非显著性，即所有系数不太可能同时为零。反之，接受零假设H0，自变量系数同时具有非显著性，即所有系数很可能同时为零。

举例说明

若给定条件 α = 0.01，F1–α(1, 250) = 6.7373。计算统计量F = 549.7 > 6.7373，表明可以显著地拒绝H0。也可用p值，如果 p值小于 α，则可以拒绝零假设H0。

$p\text{-value}=\mathsf{P}\Big(F<F_{\alpha}\left(k-1,n-k\right)\Big)$

四、t检验：某个回归系数是否为0

线性回归中，t检验主要用于检验线性回归模型中某个特定自变量的系数是否显著，而不能判断模型整体是否显著。

1、统计量

b1的 t检验统计量：

$t_{b1}=\frac{\hat{b}_{1}-b_{1,0}}{\mathrm{SE}\Big(\hat{b}_{1}\Big)}$

其中，b1ˆ为最小二乘法 OLS线性回归估算得到的系数， SE 为其标准误：

$\mathrm{SE}\left(\hat{b_1}\right)=\sqrt{\frac{\mathrm{MSE}}{\sum_{i=1}^n\left(x^{(i)}-\overline{x}\right)^2}}=\sqrt{\frac{\sum_{i=1}^n\left(e^{(i)}\right)^2}{\sum_{i=1}^n\left(x^{(i)}-\overline{x}\right)^2}}$

再其中，MSE为前面的残差平均值 (mean squared error)，n是样本数据的数量 (除NaN)。标准误越大，回归系数的估计值越不可靠。

2、假设检验

对于一元线性回归，t检验原假设和备择假设分别为：

$\begin{cases}H_0:b_1=b_{1,0}\\H_1:b_1\neq b_{1,0}\end{cases}$

零假设是特定回归系数等于零，即自变量对因变量没有显著的影响。如果 t检验的 p值小于设定的显著性水平，就可以拒绝零假设，认为该自变量的系数是显著不为零的，即自变量对因变量有显著的影响。

3、临界值

如果下式成立，接受零假设H0，否则，则拒绝零假设H0。（下面的T即b1统计量t）

$-t_{1-\alpha/2,n-2}<T<t_{1-\alpha/2,n-2}$

特别地，如果原假设和备择假设为：

$\begin{cases}H_0:b_1=0\\H_1:b_1\neq0\end{cases}$

如果临界不等式成立，接受零假设H0，即回归系数不具有显著统计性；白话说，也就是 b1 = 0，意味着自变量和因变量不存在线性关系。否则，则拒绝零假设H0，即回归系数具有显著统计性。

4、截距项系数

对于一元线性回归，对截距项系数 b0的假设检验程序和上述的斜率项系数b1类似。b0的 t检验统计量：

$t_{b0}=\frac{\hat{b}_{0}-b_{0,0}}{\mathrm{SE}\Big(\hat{b}_{0}\Big)}$

与上面的定义类似，其中：

$\mathrm{SE}\left(\hat{b_0}\right)=\sqrt{\frac{\sum_{i=1}^n\left(\varepsilon^{(i)}\right)^2}{n-2}\left[\frac1n+\frac{\overline{x}^2}{\sum_{i=1}^n\left(x^{(i)}-\overline{x}\right)^2}\right]}$

举例说明：

t检验统计值 T服从自由度为 n – 2的 t 分布。本节采用的 t检验是双尾检测。

在统计学中，双尾假设检验是指在假设检验过程中，假设被拒绝的区域位于一个统计量分布的两个尾端，
即研究者对于一个参数或者统计量是否等于某一特定值，不确定其比该值大或小，
而是存在两种可能性，因此需要在两个尾端进行检验。

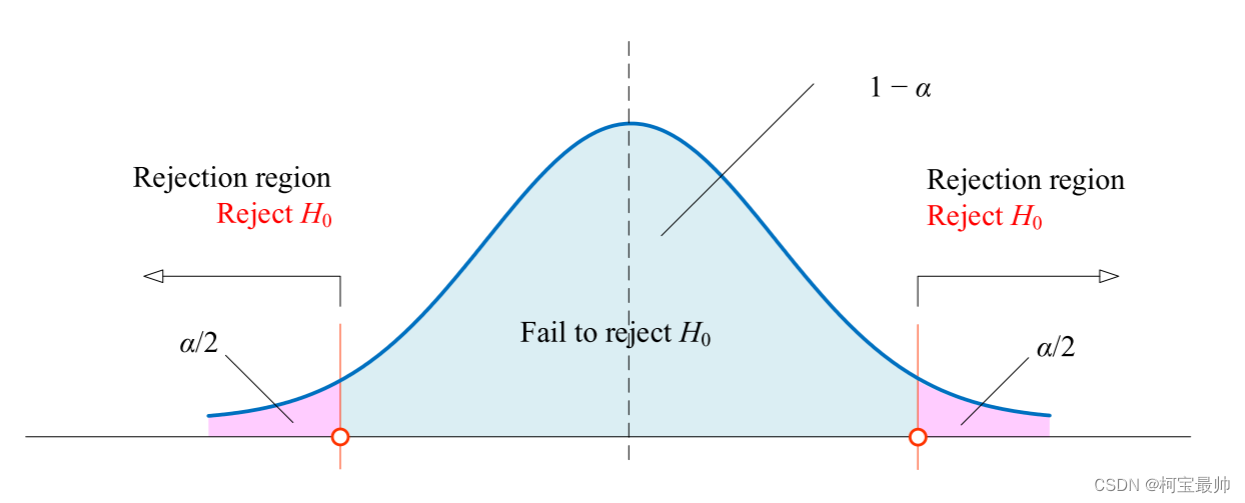
比如给定显著性水平 α = 0.05 和自由度 n – 2 = 252 - 2 = 250，可以查表得到 t值如下，Python中可以用 stats.t.ppf(1 - alpha/2, DFE) 计算两值：

$t_{1-\alpha/2,n-2}=t_{0.975,250}=1.969498$

由于t-分布对称，所以可得：

$t_{\alpha/2,n-2}=t_{0.025,250}=-1.969498$

假如计算的统计量为tb1 = 23.446，大于1.969498，则表明参数 b1的 t检验在 α = 0.05 水平下是显著的，也就是可以显著地拒绝 H0: b1 = 0，从而接受H1:b1 ≠ 0。回归系数的标准误差越大，回归系数的估计值越不可靠。

因此，斜率项系数 b1的 1 – α 置信区间如下，含义是真实 b1在以上区间的概率为 1 – α：

$\hat{b}_1\pm t_{1-\alpha/2,n-2}\cdot\mathrm{SE}\!\left(\hat{b}_1\right)$

同理，截距项系数 b0的 1 – α 置信区间为，含义是真实 b0在以上区间的概率为 1 – α：

$\hat{b_0}\pm t_{1-\alpha/2,n-2}\cdot\mathrm{SE}\!\left(\hat{b_0}\right)$

五、置信区间、预测区间

大家都应该见过类似下图的图像。左图带宽代表一元线性回归预测值的置信区间，右图是预测值的预测区间。

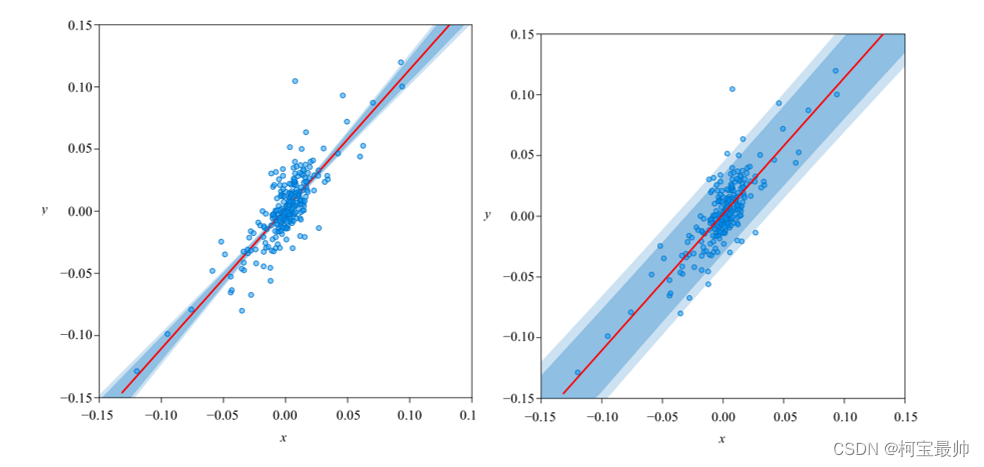
置信区间（因变量均值的区间）

在回归分析中，置信区间用于评估回归模型的预测能力（精度）。通常，预测值的置信区间越窄，说明模型预测的精度越高。

预测值 $\hat{y}^{(i)}$ 的 1 – α置信区间：

$\hat{y}^{(i)}\pm t_{1-\alpha/2,n-2}\cdot\sqrt{\mathrm{MSE}}\cdot\sqrt{\frac1n+\frac{\left(x^{(i)}-\overline{x}\right)^2}{\sum_{k=1}^n\left(x^{(k)}-\overline{x}\right)^2}}$

置信区间的宽度：

$2\times\left\{t_{1-\alpha/2,n-2}\cdot\sqrt{\mathrm{MSE}}\cdot\sqrt{\frac1n+\frac{\left(x^{(i)}-\overline{x}\right)^2}{\sum_{k=1}^n\left(x^{(k)}-\overline{x}\right)^2}}\right\}$

随着 $\left|x^{(i)}-\overline{x}\right|$ 不断增大，置信区间宽度不断增大。当 $x^{(i)}=\overline{x}$ 时，置信区间宽度最窄。随着 MSE
(mean square error) 减小，置信区间宽度减小。

预测区间（因变量特定值的区间）

指回归模型估计时，对于自变量给定的某个值 xp，求出因变量 yp的个别值的估计区间：

$\hat{y}_p\pm t_{1-\alpha/2,n-2}\cdot\sqrt{\mathrm{MSE}}\cdot\sqrt{1+\frac1n+\frac{\left(x_p-\overline{x}\right)^2}{\sum_{k=1}^n\left(x^{(k)}-\overline{x}\right)^2}}$

与预测值的置信区间不同，预测区间同时考虑了预测的误差和未来观测值的随机性，包含两个方面的误差：回归方程中的估计误差和对未来观测值的随机误差，也因此更宽。

六、似然函数、信息准则

1、对数似然函数：用于MLE

似然函数是一种关于统计模型中的参数的函数，用于最大似然估计MLE，表示模型参数中的似然性。在 OLS（普通最小二乘）线性回归中，假设残差 $\varepsilon^{(i)}=y^{(i)}-\hat{y}^{(i)}$ 服从正态分布 N(0, σ2)，因此：

$\Pr\Big(\varepsilon^{(i)}\Big)=\frac{1}{\sigma\sqrt{2\pi}}\exp\Bigg(-\frac{\Big(y^{(i)}-\hat{y}^{(i)}\Big)^{2}}{2\sigma^{2}}\Bigg)$

则似然函数为：

$L=\prod_{i=1}^n\mathrm{P}\left(\varepsilon^{(i)}\right)=\prod_{i=1}^n\left\{\frac1{\sigma\sqrt{2\pi}}\exp\left(-\frac{\left(y^{(i)}-\hat{y}^{(i)}\right)^2}{2\sigma^2}\right)\right\}$

我们常用对数似然函数 ln(L)：

$\ln\left(L\right)=\ln\left(\prod_{i=1}^{n}\mathrm{P}\left(\varepsilon^{\left(i\right)}\right)\right)=-\frac{n}{2}\cdot\ln\left(2\pi\sigma^{2}\right)-\frac{\mathrm{SSE}}{2\sigma^{2}}$

其中，在最大似然估计MLE中 σ为：

$\sigma^2=\frac{\mathrm{SSE}}{n}$

则有：

$\ln\left(L\right)=-\frac n2\cdot\ln\left(2\pi\sigma^2\right)-\frac n2$

2、信息准则：模型选择

AIC和 BIC是线性回归模型选择中常用的信息准则，用于在多个模型中选择最优模型。

①AIC为赤池信息量准则 (AIC)

$\mathrm{AIC}=2k-2\ln\left(L\right)$

其中，k = D + 1；L是似然函数。AIC鼓励数据拟合的优良性；但是，尽量避免出现过度拟合，其中 2k项为惩罚项 (penalty)。

②贝叶斯信息准则(BIC) ,也称施瓦茨信息准则(SIC)

$\mathrm{BIC=}k\cdot\ln(n){-}2\ln(L)$

其中，n为样本数据数量。BIC的惩罚项kln(n)比 AIC大。

注意：在使用 AIC 和 BIC 进行模型选择时，应该选择具有最小 AIC 或 BIC 值的模型。这意味着，较小的AIC或 BIC值表示更好的模型拟合和更小的模型复杂度。但并不保证选择的模型就是最优模型。在实际应用中，应该将 AIC和 BIC作为指导，结合领域知识和经验来选择最优模型。同时，还需要对模型的假设和限制进行检验。

七、其他

1、残差分析：假设服从正态

残差分析假设残差服从均值为0正态分布！通过残差所提供的信息，对回归模型进行评估，分析数据是否存在可能的干扰。残差分析的基本思想是，如果回归模型能够很好地拟合数据，那么残差应该是随机分布的，没有明显的模式或趋势。残差分析可以提供关于模型拟合优度的信息。

步骤：

1、绘制残差图。残差图是观测值的残差与预测值之间的散点图。
如果残差呈现出随机分布、没有明显的模式或趋势，那么模型可能具有较好的拟合优度。
2、检查残差分布。通过绘制残差直方图或核密度图来检查残差分布是否呈现出正态分布或近似正态分布。
如果残差分布不是正态分布，那么可能需要采取转换或其他措施来改善模型的拟合。
3、检查残差对自变量的函数形式。通过绘制残差与自变量之间的散点图或回归曲线，来检查残差是否
随自变量的变化而呈现出系统性变化。
如果存在这种关系，那么可能需要考虑增加自变量、采取变量转换等方法来改善模型的拟合。

为了检测残差的正态性，可以利用Omnibus正态检验，Omnibus正态检验利用残差的偏度 S和峰度 K，检验残差分布为正态分布的原假设。Omnibus正态检验的统计值为偏度平方、超值峰度平方两者之和。Omnibus正态检验利用 χ2检验 (Chi-squared test)。

2、自相关检测：Durbin-Watson

Durbin-Watson用于检验序列的自相关。在线性回归中，自相关 (autocorrelation) 用来分析模型中的残差与其在时间上的延迟版本之间的相关性。当模型中存在自相关时，它可能表明模型中遗漏了某些重要的变量，或者模型中的时间序列数据未被正确处理。
自相关可以通过检查残差图来诊断。如果残差图表现出明显的模式，例如残差值之间存在周期性关
系或呈现出聚集在某个区域的情况，那么就可能存在自相关。在这种情况下，可以通过引入更多的自变量或使用时间序列分析方法来修正模型。

Durbin-Watson检测的统计量为：

$DW=\frac{\sum_{i=2}^n\left(\left(y^{(i)}-\hat{y}^{(i)}\right)-\left(y^{(i-1)}-\hat{y}^{(i-1)}\right)\right)^2}{\sum_{i=1}^n\left(y^{(i)}-\hat{y}^{(i)}\right)^2}$

上式本质上检测残差序列与残差的滞后一期序列之间的差异大小。DW值的取值区间为 0 ~ 4。当DW值很小时 (DW < 1)，表明序列可能存在正自相关。当DW值很大时 (DW > 3) 表明序列可能存在负自相关。当DW值在 2附近时 (1.5 < DW < 2.5)，表明序列无自相关。其余的取值区间表明无法确定序列是否存在自相关。该知识点更多详情

3、条件数：多重共线性

在线性回归中，条件数 (condition number) 常用来检验设计矩阵 $X_{k\times k}$ 是否存在多重共线性，多重共线性是指在多元回归模型中，独立变量之间存在高度相关或线性关系的情况。多重共线性会导致回归系数的估计不稳定，使得模型的解释能力降低，甚至导致模型的预测精度下降。讲到多元回归分析时，条件数的作用更明显。

对 $X^\mathrm{T}X$ 进行特征值分解，得到最大特征值 λmax和最小特征值 λmin。条件数的定义为两者的比值的平方根：

$\text{condition number}=\sqrt{\frac{\lambda_{\max}}{\lambda_{\min}}}$

八、总结

这些概念是线性回归分析中非常重要的指标，可以帮助我们评估模型的拟合程度、系数显著性、预测能力和多重共线性等问题。这些概念涉及的公式可能较为复杂，但是不用完全记忆，理解它的目的是什么，大致用哪些量计算就可！

方差分析可以评估模型的整体拟合优度，其中的 F 检验可以用来线性模型参数整体显著性，t 检验可以评估单个系数的显著性。

拟合优度指模型能够解释数据变异的比例，常用 R2 来度量。

AIC 和 BIC 用于模型选择，可以在模型拟合度相似的情况下，选出最简单和最有解释力的模型。

自相关指误差项之间的相关性，可以使用 Durbin-Watson检验进行检测。

条件数是用于评估多重共线性的指标，如果条件数过大，可能存在严重的多重共线性问题。

标签：线性回归算法回归

本文转载自: https://blog.csdn.net/weixin_51658186/article/details/134930675
版权归原作者 柯宝最帅 所有，如有侵权，请联系我们删除。

【AI底层逻辑】——“数学华尔兹”之一元线性回归

一、方差分析ANOVA

1、平方和：SST、SSE、SSR

2、自由度DF

3、MST、MSR、MSE、RMSE

二、拟合优度

1、决定系数

2、修正决定系数

三、F检验：模型参数不全为0

1、统计量

2、假设检验

3、临界值

四、t检验：某个回归系数是否为0

1、统计量

2、假设检验

3、临界值

4、截距项系数

五、置信区间、预测区间

六、似然函数、信息准则

1、对数似然函数：用于MLE

2、信息准则：模型选择

七、其他

1、残差分析：假设服从正态

2、自相关检测：Durbin-Watson

3、条件数：多重共线性

八、总结

发表评论

“【AI底层逻辑】——“数学华尔兹”之一元线性回归”的评论:

关于作者

overfit同步小助手

相关阅读

文章导航