大家好,今天为各位分享最新开源的文章《Robust Beamforming with Gradient-based Liquid Neural Network》。这篇文章发表在通信领域国际权威期刊 IEEE Wireless Communications Letters上。
这篇文章首次提出了基于梯度的液态神经网络,在保证高于既有算法的频谱效率的同时,获得了显著更高的鲁棒性,同时仅需很低的计算用时(既有算法的1.6%,数十毫秒)。
文章代码已开源,欢迎下载!Gitee Github
原文链接
IEEE Xplorehttp://ieeexplore.ieee.org/document/10620247
Arxivhttp://arxiv.org/abs/2405.07291
引言
在未来的移动通信技术中,mmWave大规模MIMO是实现高数据率和低延迟通信的关键技术。然而,信道的高动态和大规模优化问题给传统波束成形技术带来了挑战。本文提出了一种创新的基于梯度的液态神经网络(GLNN),该网络利用流形学习和液态神经元优化技术,显著提高了系统的频谱效率和计算效率,具有很高的应用潜力。
6G通信技术的研究已逐渐启动,其中mmWave大规模MIMO技术是实现超高数据传输率和超低延迟的关键。传统的波束成形算法在处理高动态信道时存在性能瓶颈。为了解决这些问题,本文提出了一种基于梯度的液态神经网络(GLNN)方案,以提升系统的鲁棒性和操作效率。
highlights
- 提出了基于梯度的液态神经网络(GLNN):用于解决mmWave大规模MIMO通信中的波束成形问题,结合了流形学习技术和液态神经网络(LNN),通过基于梯度的学习方法形成一个统一协作的框架。
- ODE基础结构:液态神经元建模一阶常微分方程(ODE),使GLNN能够有效地从动态且噪声较多的信道状态信息中学习,增强模型的适应能力。
- 高阶信息提取与优化空间压缩:GLNN利用梯度学习提取输入数据的高阶信息,并通过流形学习技术压缩优化空间。
在Gradient-based optimization, manifold learning和liquid neural network三个技术共同作用下,GLNN相对于传统的优化算法,在获得更高频谱效率、更强鲁棒性的同时,只需要原来1.6%的优化时间。
系统模型与问题表述


这个问题是高度非凸和非线性的,优化问题是NP-hard问题。
GLNN的原理与架构
流形学习技术
在传统的波束成形问题中,优化空间随着天线数量的增加而显著增大,导致计算复杂度急剧上升。GLNN通过引入流形学习技术压缩搜索空间,将高维的优化问题转化为低维的流形优化问题,从而降低了问题的复杂度并提高了算法的效率。
可以证明 ,最优的波束赋形向量必然可以表示为

液态神经网络结构
液态神经网络(LNN)是一种模拟生物神经系统的动态响应的神经网络结构,其通过普通的微分方程(ODE)来模拟神经元的时间变化行为。GLNN采用液态神经网络作为核心结构,能够有效处理高动态和噪声环境下的信号,提高了波束成形的准确性和鲁棒性。


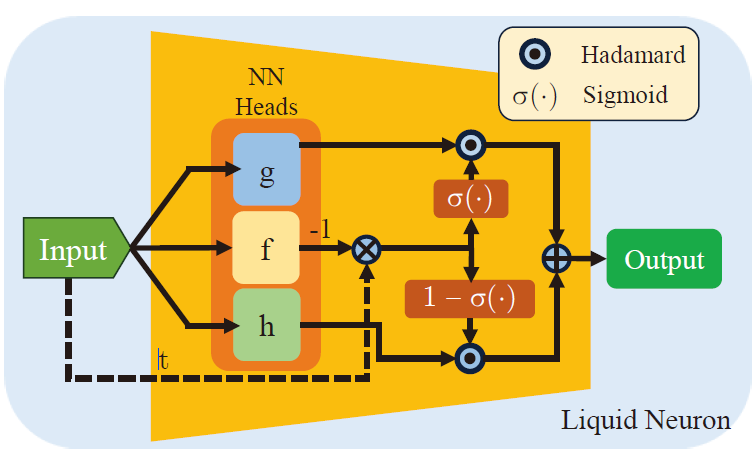
一个液态神经元
基于梯度的优化
GLNN利用目标函数的梯度信息作为输入,配合液态神经网络的动态特性,能够更深入地提取信号的高阶特征,实现更精确的优化。先前基于深度学习(DL)的波束成形方案通常将原始信道矩阵 输入到神经网络(NN)中,并直接将输出用作预编码矩阵 。然而,由于优化空间的高度非凸性,传统的基于NN的架构很难从该空间中提取高阶信息,这可能会降低整体性能。为了解决这个问题,我们引入了梯度优化技术,该技术将优化目标的梯度输入到NN中。

GLNN架构
将以上的技术融合,形成GLNN框架。如图。
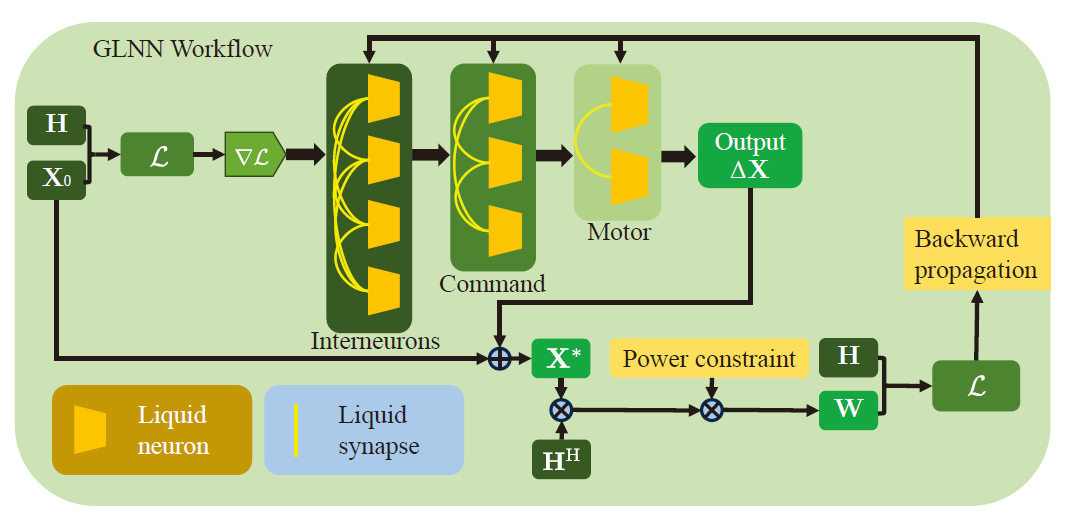
GLNN框架
为了进一步提升频谱效率,关注用户公平,在优化函数中增加了惩罚项:

在上述技术的作用下,GLNN除输入和输出层外,仅仅需要30个隐藏神经元就可以在数十毫秒内计算出比传统方法更优的波束赋形矩阵。
仿真验证
通过对比其他基线算法,GLNN在频谱效率上显示出显著优势。仿真结果表明,GLNN在保持低复杂度的同时,频谱效率比最优迭代算法高出4.15%,计算时间仅为传统方法的1.61%。这一显著的性能提升归功于其高效的结构设计和优化策略。
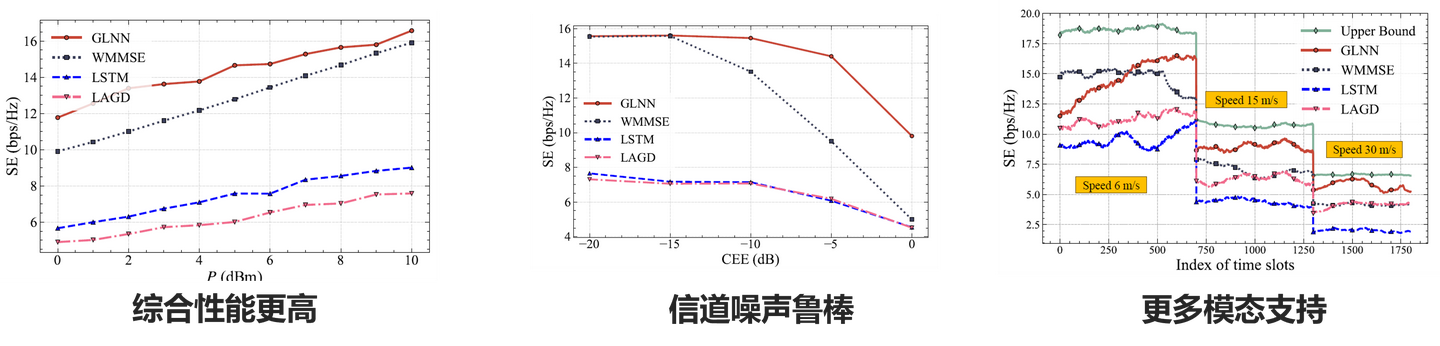
结论
GLNN框架通过整合流形学习技术和基于ODE的液态神经网络,提供了一种新的解决方案,用于解决大规模MIMO系统中的波束成形问题。其强大的性能和低复杂度的特性使其成为未来无线通信领域的一个有力技术方案。
版权归原作者 无线智能通信 所有, 如有侵权,请联系我们删除。