【初阶数据结构与算法】第八篇——二叉树的顺序结构的应用（堆排序+TOPK问题）

​

⭐️本篇博客我要给大家分享一下二叉树顺序结构应用。希望对大家有所帮助。
⭐️ 博主码云gitee链接：码云主页

💙系列文章💙

【初阶数据结构与算法】第一篇：算法中的时间复杂度和空间复杂度

【初阶数据结构与算法】第二篇：顺序表

【初阶数据结构与算法】第三篇：单链表

【初阶数据结构与算法】第四篇：链表面试题详解

【初阶数据结构与算法】第五篇：双链表

【初阶数据结构与算法】第六篇：栈和队列（各个功能实现+练习题包含多种方法）

【初阶数据结构与算法】第七篇：二叉树和堆的基本概念+以及堆的实现

前言

​

🌏一、堆排序

** **🍯1.堆排序概念

⭐️堆排序：是通过建立大堆或者小堆来排序的算法

🍯2.堆排序方法实现和代码

🍍建立堆（以下以建立大堆为例）

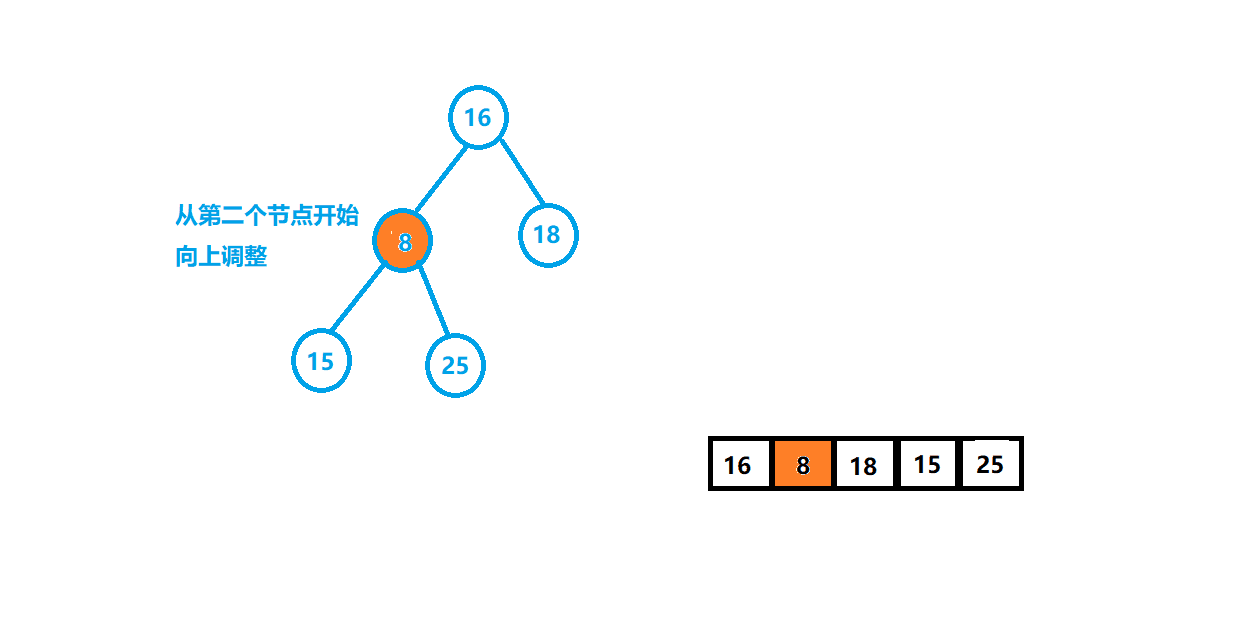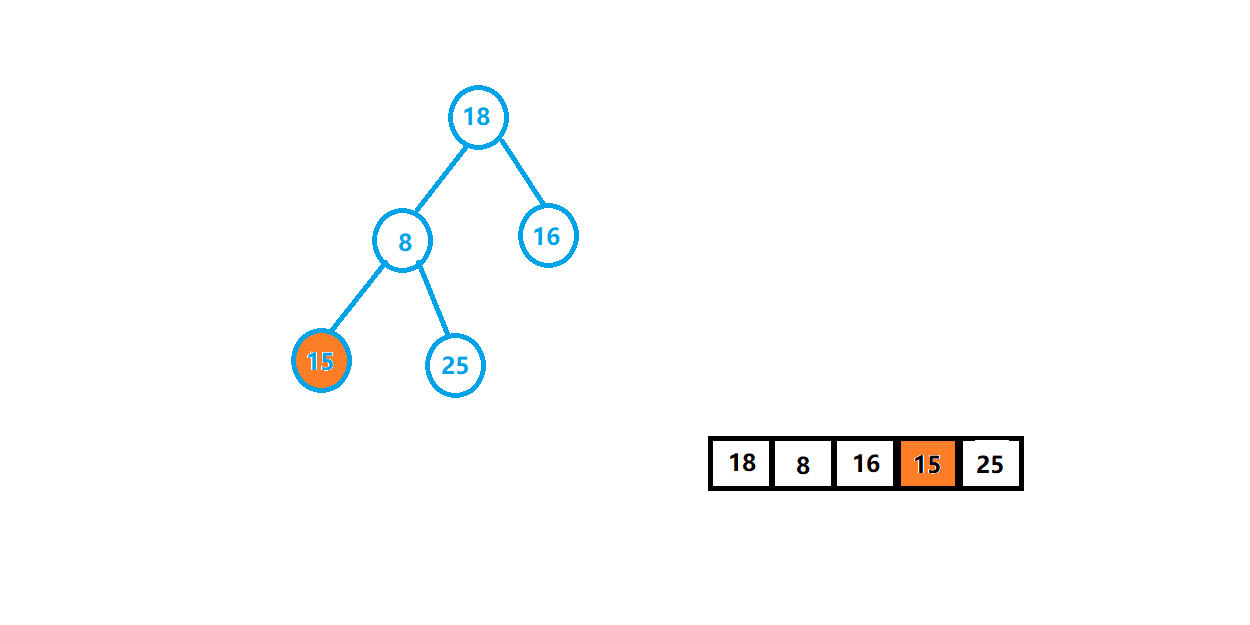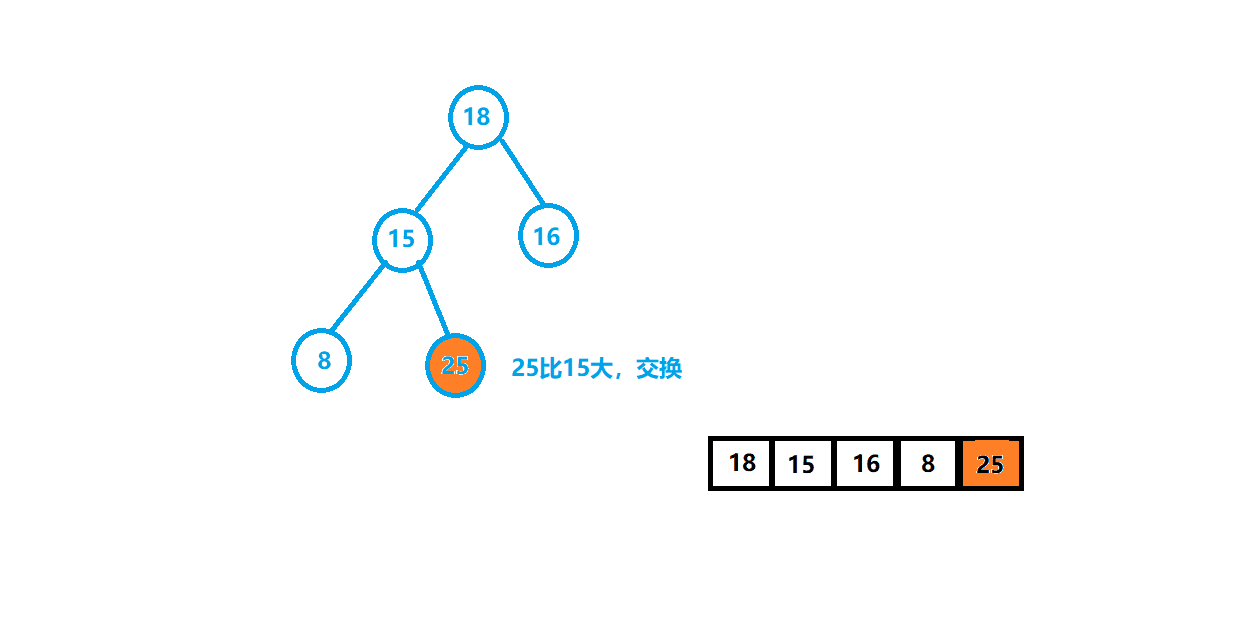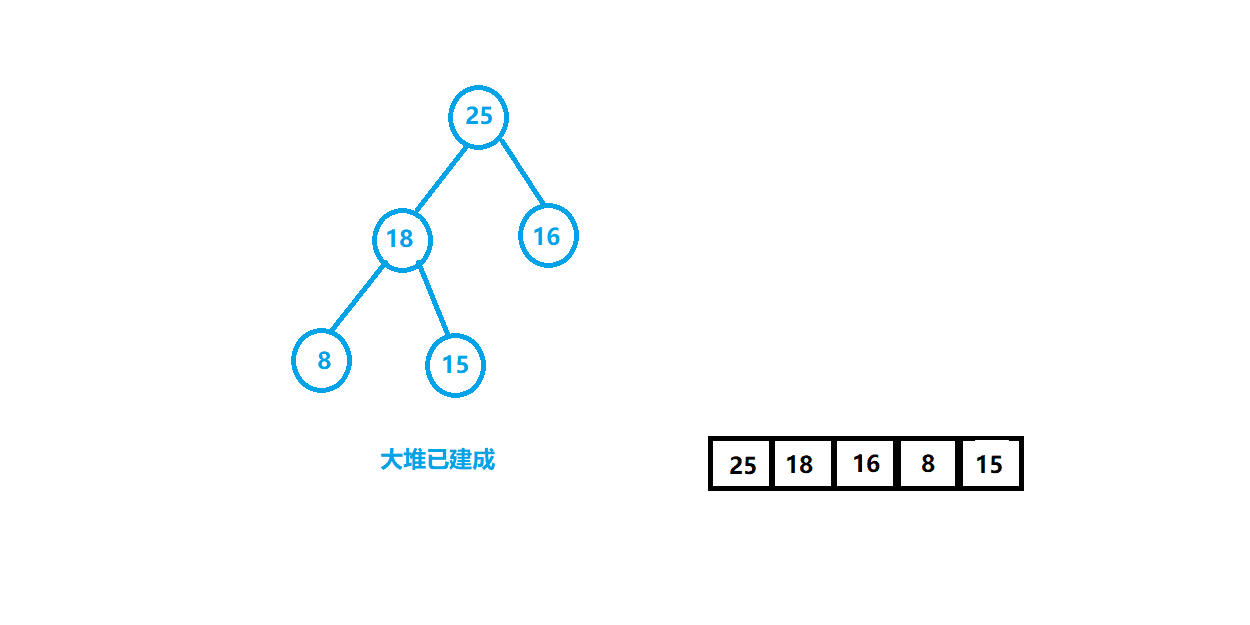
⭐️第一种：使用向上调整插入数据的思想建立堆，将第一个数字看成堆，之后插入的数据要进行向上调整

void AjustUp(int* a, size_t child);

void HeapSort(int* a, int size) {
    //向上调整，建堆
    for (int i = 1; i < size; i++) {
        AjustUp(a, i)
    }
}

⭐️第二种：向下调整，首先从非叶子节点开始（一个叶子节点既可以看作小堆，也可以看作大堆，不会影响结构，所以从倒数第1个非叶子节点开始），最后一个节点是n-1，那么最后一个非叶子节点就是(n-1-1)/2

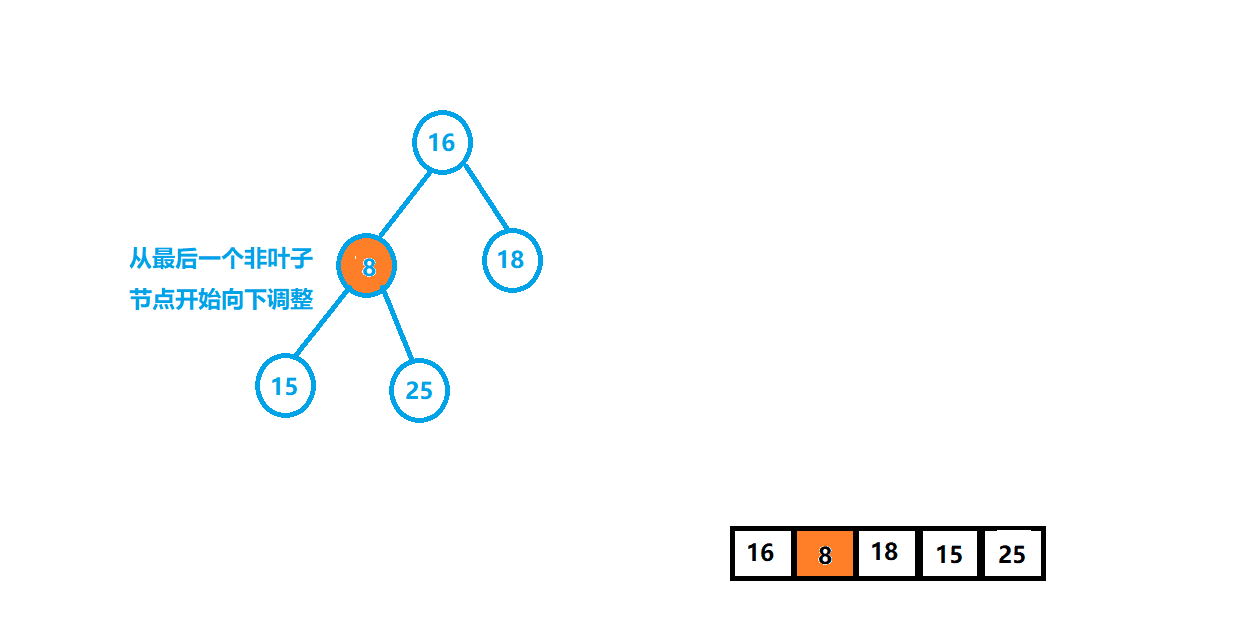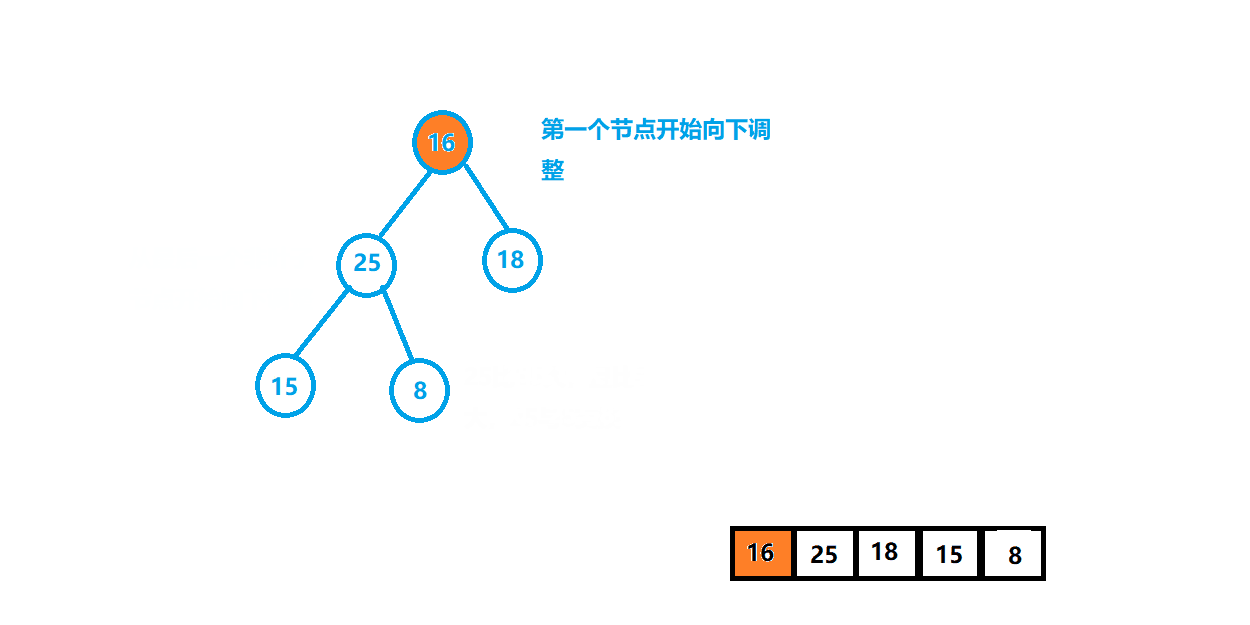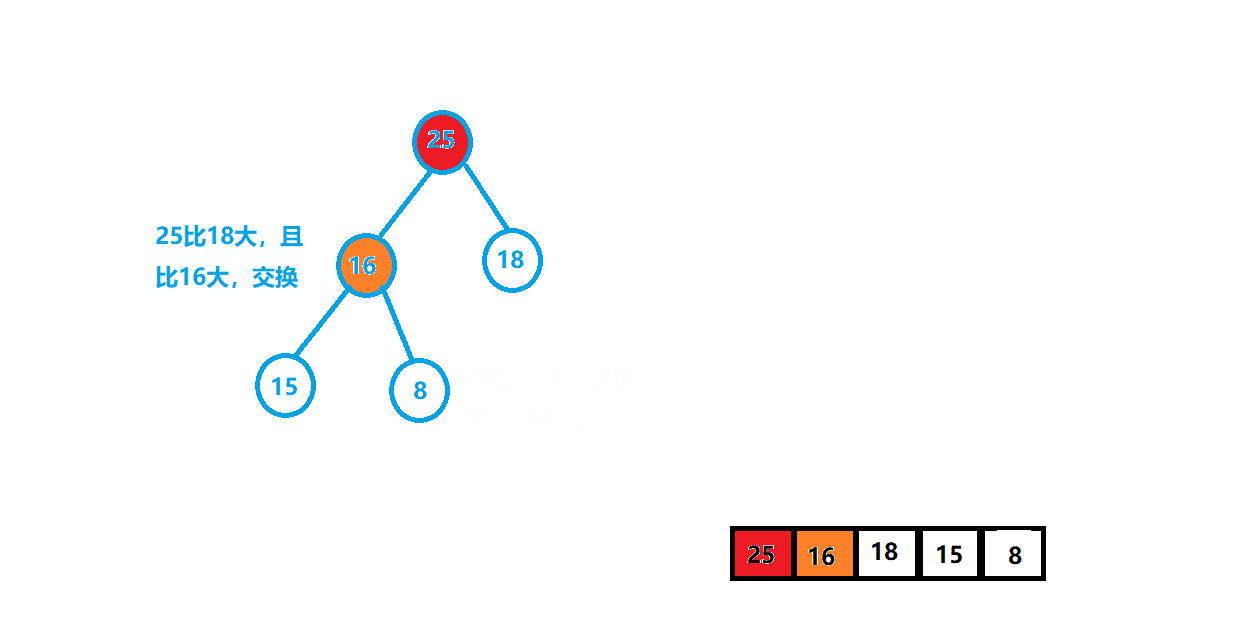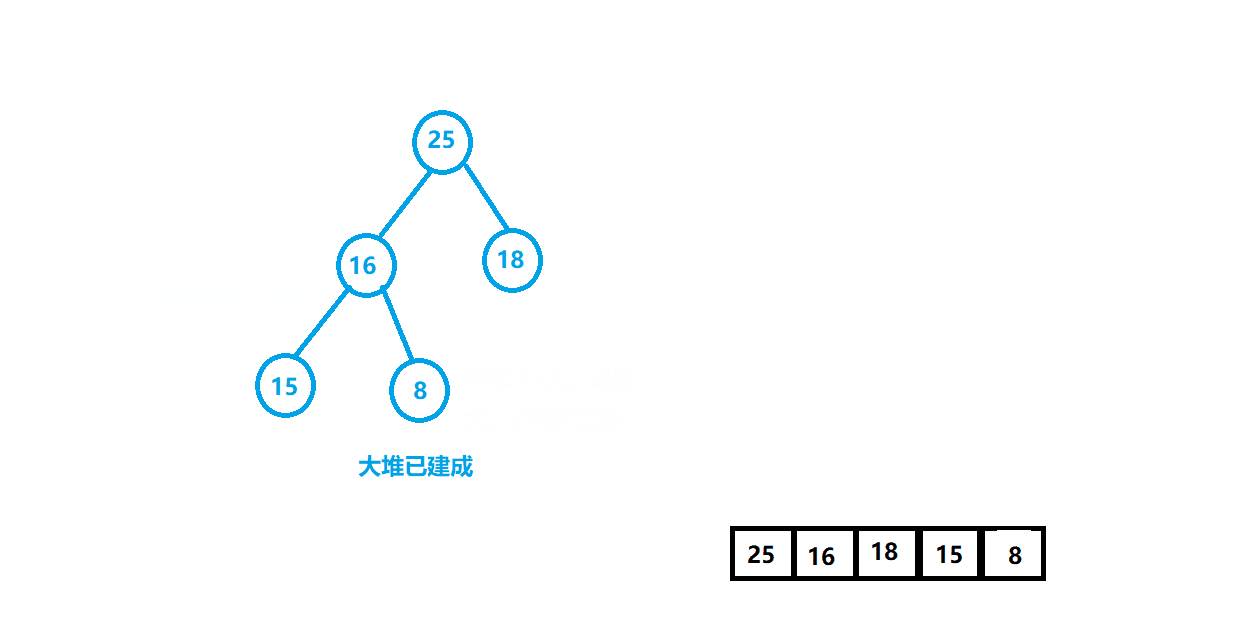
void HeapSort(int* a, int size){
    int parent = (n - 1 - 1) / 2;
    int i = 0;
    for (i = parent; i >= 0; i--)
    {
        //建大堆 向下调整
        AdjustDown(hp->a, n, i);
    }
}

🍍排序选择堆

🔑升序和降序选择大堆小堆？

⭐️ 升序选大堆，降序选小堆

    升序如果选小堆，那么如果第一个数字是最小的，那么选出第二小的数的时候，就要重新建堆，使后面队形散乱，所以升序要选大堆。相反降序就选小堆。

void HeapSort(HPDataType* a, int n)
{
    //找到最后一个父亲节点
    int parent = (n - 1 - 1) / 2;
    int i = 0;
    //建小堆 排降序  建大堆 排升序
    for (i = parent; i >= 0; i--)
    {
        //建大堆 向下调整
        AdjustDown(a, n, i);
    }

    i = n - 1;
    while (i >= 0)
    {
        Swap(&a[0], &a[i]);
        AdjustDown(a, i, 0);
        i--;
    }
}

⭐️时间复杂度是o(n*logn),建立堆时间复杂度是o(n),排序是o(logn)

⭐️空间复杂度是O(N)

🌏二、TOP-K问题

⭐️****TOPK问题：找出N个数里面最大/最小的前K个问题。

⭐️思路：用K个数建立K个数的小堆（如果建大堆，最大的数可能挡在头的位置，其他9个次大的数就进不来），用然后剩下的N-K个数依次遍历，如果比堆顶的数据打，就替换他进堆（向下调整），最后堆里面的K个数就是最大的K个

oid PrintTopk(int* a, int n, int k) {
    //1.建堆，用a选中钱k个元素建堆
    int* kminHeap = (int*)malloc(sizeof(int) * k);
    assert(kminHeap);

    for (int i = 0; i < k; i++) {
        kminHeap[i] = kminHeap[i];
    }
    
    int parent = (n - 1 - 1) / 2;
    int i = 0;
    for (i = parent; i >= 0; i--)
    {
        AdjustDown(kminHeap, n, i);
    }

    //2.将剩余的n-k个元素依次与堆顶元素交换，不满则直接替换
    for (int i = k; i < n; ++i)
    {
        if (a[i] > kminHeap[0])
        {
            kminHeap[0] = a[i];
            AdjustDown(kminHeap, k, 0);
        }
    }

void TestTopk()
{
    //随机取十个很大的数
    int n = 100000;
    int* a = (int*)malloc(sizeof(int) * n);
    srand(time(0));
    for (size_t i = 0; i < n; ++i)
    {
        a[i] = rand() % 1000000;
    }
    //随机赋值十个最大的数
    a[5] = 1000000 + 1;
    a[1231] = 1000000 + 2;
    a[531] = 1000000 + 3;
    a[5121] = 1000000 + 4;
    a[115] = 1000000 + 5;
    a[2335] = 1000000 + 6;
    a[9999] = 1000000 + 7;
    a[76] = 1000000 + 8;
    a[423] = 1000000 + 9;
    a[3144] = 1000000 + 10;

    PrintTopK(a, n, 10);
}

⭐️首先开辟好十个空间，存放前K个数据，再将这K个数据建立为小堆， 之后将剩下N-K个数据依次向上调整(此时K数组中第一个数据是最小的)，然后在向上调整。

⭐️复杂度分析：时间复杂度O(K+logK(N-K)),建堆是O(K),向下调整是(N-K)*logK，当N很大，K很小时，可以等价于O(N)

⭐️空间复杂度是O(K)

🌏总结

    有时候觉得世界上聪明的人还是越多越好，一般人谁会想到这种方式呢