汉诺塔 问题 python 解决

汉诺塔问题？

汉诺塔是根据一个传说形成的一个问题。汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆## 标题盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

此处 奉上盗版玩具图一张

思考步骤

先来看看两个圆盘的解决方案：

如果有两个盘子时，移动方案如下：
A—>B #借助B，帮助C拿到最后一个盘子
A—>C #最后一个盘子移动完成后，剩余的盘子已经全部到B上了
B—>C #将剩余的盘子移动到C上，完成
一共就需要了三步

那如果有三个盘子呢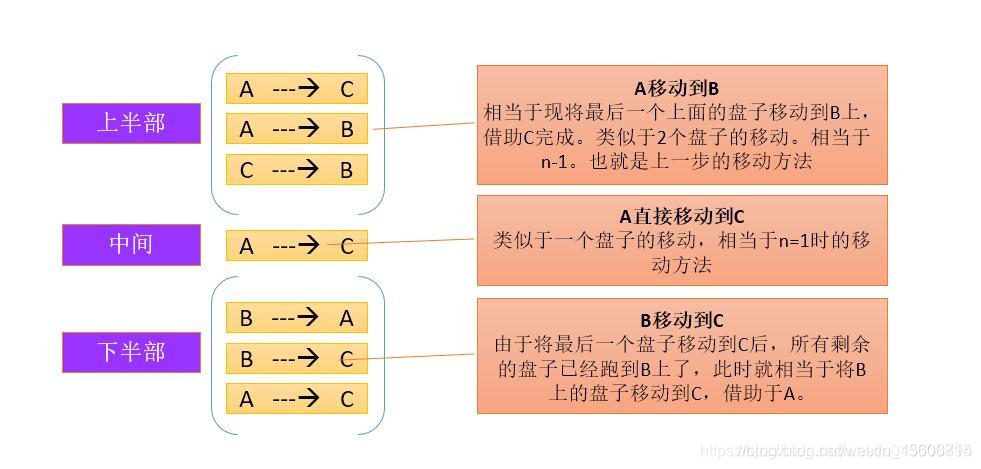

加起来则就为7步

那如果是n个盘子的问题呢 我们的思考是 利用递归的思想来解决这个问题
(因为要将第n个大盘子移动的前提是 将 前n-1个小盘子 移动到另一个柱子上)

经过上面例子，我们可以发现如下规律：
当盘子只有一个是，即N=1,只有一个动作，从A移动到C即结束
当有N个盘子时：
上半部分： 移动一定和n-1盘子移动时的动作相同。出发地都是A,只不过，n-1个盘子移动的目的是B，而不是C。这样方便取出最后一个盘子
中间部分： 一定是由A移动到C
下半部分： 此时等待移动的盘子已经都在B上，而不是A上，移动步骤类似于n-1个盘子的移动。出发地是B，目的地是C

递归分析

如果想要移动n个盘子到指定目的，那么一定要先将n-1个盘子移动到备用柱上。
当n-1个盘子移动后，必定要将最后一个盘子移动到C上。
经过上面的调换后，剩下待处理的盘子还有n-1个，此时盘子已经在B上而不是在A上。此时需要从新判断剩余的盘子个数。如果依然大于1个那么还是需要按照1的步骤移动第n-1个盘子之上的所有盘子共n-2到A上。从而好让第n-1个盘子从B移动到C。
总结：到第3步时，发现和有和第一步第二步类似地方。只需要改变盘子的出发点和目的点，就能刚好递归

代码实现

defmove(n,a,b,c):if n==1:print(a,'--->',c)else:
        move(n-1,a,c,b)print(a,"--->",c)
        move(n-1,b,a,c)
move(3,"a","b","c")

可以发现 输出了正确的结果：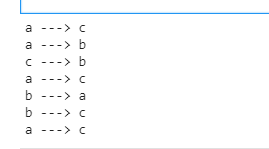

但是当我们运行计算64个盘子的时候 我们发现 计算机可能都算不出来

defmove(n,a,b,c):if n==1:print(a,'--->',c)else:
        move(n-1,a,c,b)print(a,"--->",c)
        move(n-1,b,a,c)
move(64,"a","b","c")

公式解决汉诺塔移动的次数

但是我们通过 发现 汉诺塔运算结果的规律
三个盘子：

四个盘子：

五个盘子：

XSWL 难道这不就是 通式 2^n-1 嘛
所以在这里奉上 计算汉诺塔移动步数的公式：

n=64print("汉诺塔移动步数:",2**n-1)

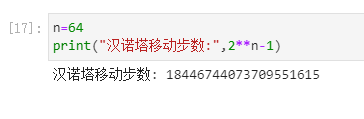
不得不说 这该死的数学的魅力啊！