
如果你刚刚开始机器学习生涯,那么你可能会偶然发现精确(Precision )和召回(Recall )的概念。这些术语在研究模型评估的概念时经常出现。
通常情况下,初学者很难理解这些概念。不是因为它们很难,而是因为相同的令人困惑的技术和定义被一次又一次地使用。通常,概念将通过先定义术语,然后展示模型评估的真实例子来解释。让我们来看几个例子。第一个摘自谷歌的机器学习速成课程:
Precision attempts to answer the following question: What proportion of positive identifications was actually correct? [1]
Recall attempts to answer the following question: What proportion of actual positives was identified correctly? [1]
在大多数文献中,这是您会找到的定义。我不太确定为什么这种文字游戏是描述这两个术语的标准,但有时会非常令人困惑,尤其是对于初学者。尽管它们不是,但这两个定义的措辞看起来好像它们的意思相同。那么也许我们可以找到更好的解释?Scikit Learn 的文档定义如下:
Precision (P) is defined as the number of true positives (Tp) over the number of true positives plus the number of false positives (Fp) [2]
Recall (R) is defined as the number of true positives (Tp) over the number of true positives plus the number of false negatives (Fn) [2]
除了如何计算精确率和召回率的值之外,这里就不多说了。让我们看最后一个例子,来自维基百科关于精确率和召回率的文章:
Precision (also called positive predictive value) is the fraction of relevant instances among the retrieved instances, while recall (also known as sensitivity) is the fraction of relevant instances that were retrieved [3]
除了措辞和词汇略有变化外,这个定义与我们看到的第一个定义非常相似,来自谷歌。
在本文中,我们将以不同的方式解释这些术语。我们不看定义,而是先看精确率和召回率的等式,并尝试从中提取尽可能多的信息。这个想法是,一旦您了解了这些术语的计算方式,您就应该有更好的基础来理解主流定义。请注意,本文不是模型评估的介绍。相反,我假设读者对何时、为什么以及如何应用这些概念有基本的了解,但正在寻找更好的方式来理解它们。
决策矩阵
我们不会详细介绍分类结果之间的差异,因为这不是本文的重点。如果您不知道什么是决策矩阵,并且不完全了解真阳性、假阳性、真阴性和假阴性之间的区别,那么我们建议您阅读我们公众号中以前发布的相关文章。
但是,如果您理解了这些概念并且只需要快速复习一下,那么这里有一组分类问题中四种可能结果的快速定义:
True Positive (TP):分类模型将一个数据点标记为正,而该数据点实际上是正的。
False Positive (FP):分类模型将一个数据点标记为正,而该数据点实际上是负的。
True Negative (TN):分类模型将一个数据点标记为负数,而该数据点实际上是负数。
False Negative(FN):分类模型将一个数据点标记为负,而该数据点实际上是正的。
Precision、Recall 和 Precision vs Recall
准确率和召回率
理解准确率和召回率的计算方式并不比理解基本百分比难。
考虑一个场景,您有一篮子 10 个水果,其中三个是苹果,其余是橙子。你如何计算你的篮子里有多少苹果?我们使用基本百分比公式(部分/整体)* 100,其中部分是您希望获得百分比的项目子集的数量,而整体是您集合中项目的总数。所以 (3/10)*100 = 30%。很简单吧?
让我们看看我们如何计算精度:

我们可以从这个方程中提取什么信息?好吧,首先请注意,分子和分母中都使用了真阳性的总数。然而,在分母中,我们添加了一个额外的术语,即误报的数量。这个增加的项使得我们的精度将始终保持小于或等于 1 的值,因为分母将始终大于或等于 TP。然而,更重要的是,请注意我们如何得到分母:我们将模型归类为阳性的数据点数量相加,无论它实际上是阳性(真阳性)还是非阳性(假阳性)。所以,我们的分子是真阳性的数量,而我们的分母是所有阳性的数量。这给我们留下了什么?它给我们留下了一个数字(百分比、比率),它描述了我们的模型归类为正的数据点中有多少实际上是正的。如果您仍然感到困惑,请这样想:我们篮子里的水果有多少是苹果?30%。现在,用被归类为阳性的阳性数据点的数量替换苹果,并用被归类为阳性的阳性和阴性数据点的数量替换整个水果篮。这是相同的想法,只是传达不同的东西。
接下来,我肯看一下recall。这是它的等式:

我们可以运行与精确度完全相同的分析。分母与分子的唯一区别是在分母中添加了一个额外的值。然而,这一次,我们没有将误报的数量添加到 TP 中,而是添加了误报的数量。所以,我们的分子仍然是真阳性的数量,而我们的分母现在是应该被归类为阳性的数据点的总数,但可能是也可能不是。这给我们留下了一个数字,描述了我们的模型能够识别出多少正数据点。同样,这个数字将始终小于或等于 1。
精确与召回
在研究模型评估的概念时,我们被告知通常在精度和召回率之间进行权衡。随着精度的提高,召回率会降低,反之亦然。然而,很少有人告诉我们为什么会这样。相反,我们看到了一张类似于下图的图表:
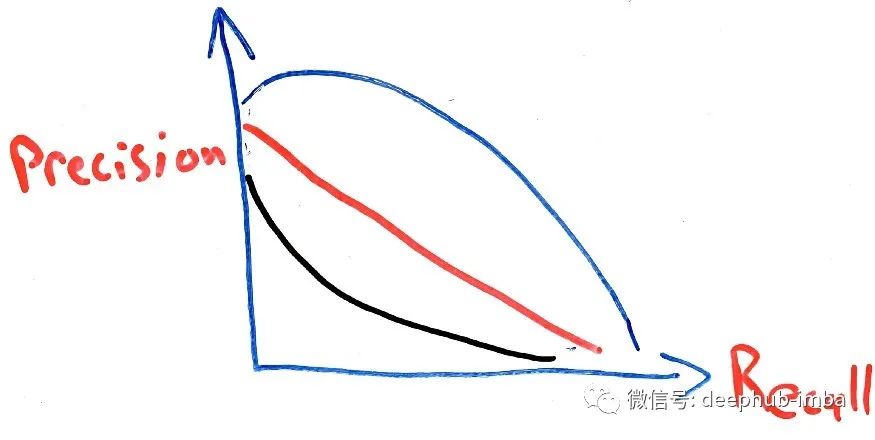
获得的曲线类型(红色、蓝色或黑色)取决于一些超参数。虽然这是一种可视化事物的好方法,但当我在数学上比较它们时,我个人更了解这两个变量之间的关系。
在使事情复杂化之前,请尝试比较这两个等式。现在,您肯定已经注意到了相似之处。将两者分开的唯一因素是我们在分母中添加到 TP 的值。这意味着什么?这意味着我们对结果的控制在于 FP 和 FN 的数量。因此,增加或减少这些值将导致我们的精度和召回率的增加或减少。
考虑以下比较:
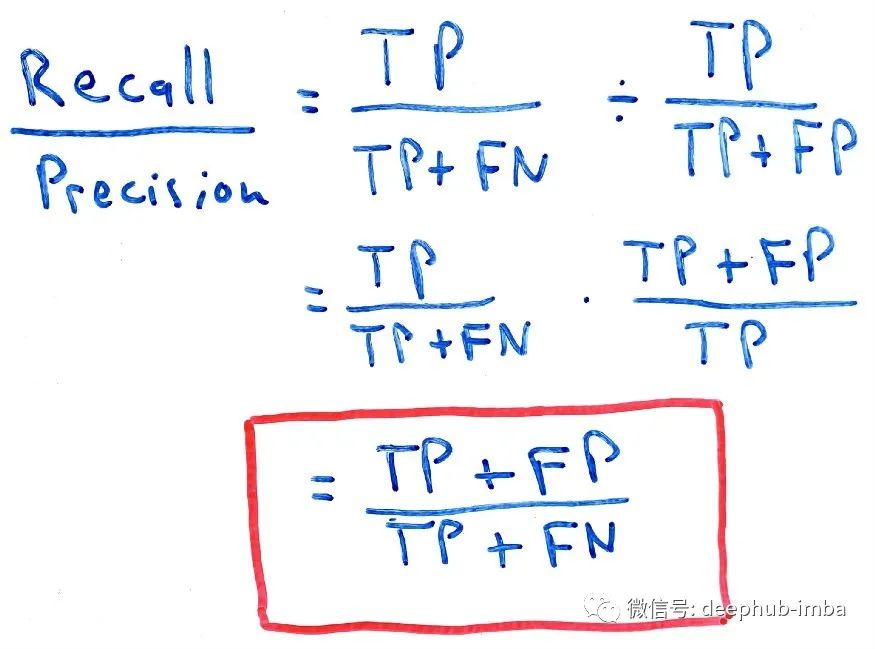
从这个结果中可以提取出很多东西:
如果 FP > FN,那么我们的召回率与精确率之比将大于 1,我们的精确率将低于我们的召回率。
如果 FP < FN,那么我们的召回率与精确率之比将小于 1,我们的精确率将大于我们的召回率。
如果 FP ~= FN,那么我们的召回率与精确率之比将等于 1,我们的精确率将等于我们的召回率。
由此,我们还可以将精度表示为召回率的函数,将召回率表示为精度的函数,以更好地理解两者之间的关系:


同样,这些方程告诉我们很多关于指标之间关系的信息。通过它们,人们可以开始通过调整不同的参数来控制模型的性能。
译者注:
这里有一张我认为比较好理解的图,大家有兴趣的可以参考
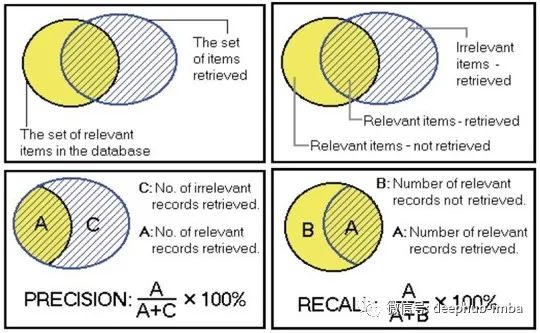
总结
本文的目的是为精确率和召回率的概念提供不同的视角。我们没有首先查看定义(传统上是如何解释概念的),而是首先提取了通过它们的方程传达的信息。从那里,我们能够很好地理解,这将我们引向当今文献中使用的传统定义。
最后,我们研究了准确率和召回率之间的关系,并得出了为什么我们经常被告知两者之间存在权衡的结论。
从这里开始,我建议您开始研究 ROC 曲线。虽然这是一个复杂得多的主题,但根据您在本文中学到的知识,您已经具备了这样做的适当知识。
引用
[1] Classification: Precision and Recall (2020), Google’s Machine Learning Crash Course
[2] Scikit-Learn Developers, Precision-Recall (2020), Scikit-Learn
[3] Precision and recall (2021), Wikipedia
作者:Ali H Khanafer
本文地址:https://ali-h-khanafer.medium.com/a-different-way-of-looking-at-precision-vs-recall-1129bcd652ad